解析法和数值法在地下水溶质运移预测评价中的对比研究

吴 瑾 贾冬梅 李学宁

(1.天津市地质环境监测总站，天津 300191；2.天津市地质调查研究院，天津 300191)

2011年 6 月，环境保护部颁布了《环境影响评价技术导则—地下水环境》(HJ 610-2011)，对建设项目环境影响评价中的地下水环评工作起到了指导与规范作用。导则中明确要求一级评价应采用数值法，二级评价中水文地质条件复杂且适宜采用数值法时建议优先采用数值法，三级评价可采用解析法或类比分析法。因此，数值法和解析法在地下水环境影响评价的预测分析中都被广泛应用。

解析法能够给出控制微分方程的精确解；数值法采用一组代数方程近似处理微分方程[1]。当水文地质条件比较简单而且己经取得足够的水文地质资料和弥散参数资料时，可采用解析法。当含水层的边界条件、结构和水文地球化学条件相对复杂、含水层之间存在越流时，数值法能够灵活处理复杂的边界条件、含水层的非均质性和各向异性等，此时宜选用数值法进行预测[2]。

数值法和解析法都有各自的优缺点。数值法的优势是可以容易的解决水流和运移参数(如水力传导系数、孔隙度、弥散度、阳离子交换量等)的分布异质性问题[3]。数值法比解析法灵活性更大，所以数值法可直接用于解决野外场地具体问题，模拟运算结果更能贴近实际。但数值法获取专业的水文地质参数较为困难，且模型建立对数据的数量质量要求严格、操作繁琐、周期较长，另外，它会导致所得的结果扩展超过与建模主体示踪剂的弥散无关的溶质锋面或污染羽[4]，这些都阻碍了数值模拟应用的范围及广度。解析法虽然对参数要求不高，操作起来也更加简便易行，但解析法在使用过程中受地质条件限制较为明显，鉴于区域因素、人为因素、环境因素的影响，在预测结果准确性上会有一定影响[5]。另外解析法仅能对一个投源点加以解析，在需要对面源进行分析时，具有一定局限性，预测结果精度不大[6]。

通过对数值法和解析法优缺点的对比，本文以某油田井场为例，分别用上述两种方法进行溶质运移预测分析，通过预测结果的比对，探索两种预测结果的差异性及对地下水环境影响评价预测分析的适宜性。

1 研究区水文地质概况

研究区位于天津市滨海新区某油田井场内，地势西高东低，多洼淀或坑塘水域，处在我国典型的淤泥质海岸岸段北部渤海湾西岸，地貌类型属于海积平原地貌。研究区场地范围主要由滨海泻湖洼地构成，地表以粘性土为主，土壤盐渍化严重，并保留有贝壳堤，为距今200～5000年海岸变迁的遗迹。

第I含水组分为潜水和微承压水，底界埋深约为70～80 m，含水层以粉细砂为主，一般4～5层，累计厚度10～20 m，东部最厚可达40 m。含水组的富水性弱，涌水量东部100～500 m3/d，西部多小于100 m3/d。咸水矿化度一般10～20 g/L。水化学类型为Cl-Na型。浅层多为咸水或咸卤水，水质差，大部分地区均为不开采。研究区地下水水位埋深较浅，场地内潜水主要靠大气降水入渗补给、地表水体入渗为主。地下径流主要是自东南向西北方向。场地内地下水排泄方式为潜水蒸发、侧向流出。

第II含水组底界埋深约为175～185 m，含水层以粉细砂为主，偶见粗砂，一般8～9层，单层厚度2～5 m，最厚约10 m。累计厚度北部40～50 m，中、南部27～36 m。其富水性由北向南变差，北部永定新河以北涌水量2 000～3 000 m3/d，向南至塘沽区中北部一带，涌水量在1 000～2 000 m3/d，导水系数100～300 m2/d。塘沽区东部和南部广大地区涌水量小于500 m3/d，导水系数50～100 m2/d。咸水的底界埋深在海河以北70～110 m，向南由110 m渐增至210 m，南部第II含水组为咸水。第II含水组总体上为淡水，北部矿化度0.4～0.9 mg/L，化学类型为HCO3-Na型，向南过渡为HCO3·Cl-Na和Cl·HCO3-Na型，矿化度0.7～1.0 mg/L，局部集中开采区地下水矿化度增高，有水质恶化趋势，矿化度增高到2.21 mg/L。本含水组是塘沽区主要开采层之一。

第III含水组底界深度约为275～285 m，含水层以细砂、粉细砂为主，偶见中砂，一般6～8层，单层厚度3～6 m，累计厚度36～43 m，向南变薄。其富水性由北向南变差。东北部涌水量在2 000～3 000 m3/d和1 000～2 000 m3/d，导水系数100～300 m3/d，向南至海河以北变为500～1 000 m3/d，海河以南多小于500 m3/d。矿化度由北向南由0.6 g/L增至1 g/L左右，水化学类型由HCO3-Na过渡为HCO3·Cl-Na型和Cl·HCO3-Na型。本含水组也是塘沽区主要开采层之一。

第IV含水组底界深度约为405～415 m，下部包括部分新近系含水层。含水层岩性以粉砂、细砂为主，偶见中砂。北部单层厚度4～6m，累计厚度40～50 m，向南变薄为30～40 m。本组富水性较差，除西部涌水量大于2 000 m3/d 外，其余大部分地区在500～1 000 m3/d，向南部富水性更差，多小于500 m3/d。矿化度在0.4～0.7 g/L，以HCO3-Na和HCO3·Cl-Na型为主[7]。

2 数值法对溶质运移预测的应用

2.1 数值模型的建立

研究区采用对流—弥散方程来描述石油类污染物在三维地下水流中的运移，溶解于地下水中NAPLs运移的数学模型可表示为：

式中：n—含水层介质有效孔隙度；c—污染质浓度(mg/L)；Dx—纵向弥散系数 (m2/s )；Vx—纵向渗流速度(m/s)；t—时间(s)；M—生物降解项；φ—模型修正系数，根据前人研究成果，取模型修正系数为0.92。研究区水文地质结构模型和参数选取分别如图1和表1所示。

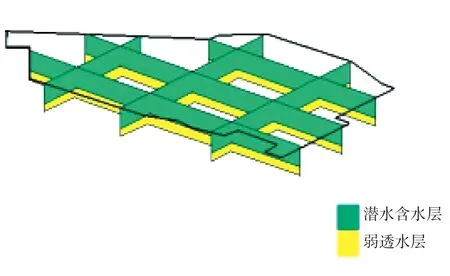
图1 水文地质结构模型图

表1 参数汇总表

研究区溶质运移模型采用三维非稳定流数学模型：

(x,y,z)εG,t>0

C(x,y,z,t)lt=0=C0(x,y,z)∈G

C(x,y,z,t)lΓ1=C1(x,y,z,t),(x,y,z)∈Γ1

式中：C为浓度；Dij为水动力弥散系数张量的分量；W为源汇项；Cw为随W注入的污染物浓度；Rd为滞留因子；n为孔隙度；ui为水流实际速度分量；G为研究区域;Γ为研究区域的边界。

研究模型在垂向上概化为两层。第一层为潜水含水层(-17～0 m)，岩性主要为粉质粘土、淤泥质粉质粘土、粉土；第二层为弱透水层(-22～-17 m)，岩性主要为粉质粘土。

研究区以井场为例，采用有限差分法，在平面上对井场进行矩形剖分，共剖分了230行200列，共计46 000个单元格，其中活动单元格15 187个，单元格长10 m，宽10 m，见图2。

图2 模拟区平面网格剖分图

由于水文地质概念模型、模型边界条件概化、源汇项及水文地质参数处理、模型识别验证及调参、污染源强设定不是本文主要研究对象，这里不再对上述过程进行详细论述。

2.2 预测结果

本次模拟选取的预测因子为石油类，石油类的标准限值参照《地表水环境质量标准》(GB3838—2002)中的Ⅲ类标准。当污染物浓度大于标准限值时，表示地下水受到污染，以此计算污染超标距离；当污染物浓度小于标准限值并大于检出限时，表示地下水受到污染的影响，但不超标，以此计算污染影响距离；当预测污染物浓度小于检出限时视同对地下水环境基本没有影响。根据预测结果，地下水中石油类在100天、1000天、30年、50年时向地下水下游方向最大超标距离见表2和图3。

100天石油类污染物运移范围图

表2 地下水中石油类迁移距离预测结果表(数值法)

3 解析法对溶质运移预测的应用

3.1 解析法原理

假设石油类泄露排放形式简化为点源，在投源点瞬时投入质量为M的示踪剂，地下水沿x轴正方向均匀等速流动，不考虑污染物在含水层中的吸附、挥发、生物化学反应等，且模型中所赋各项参数予以保守性考虑，污染物在潜水含水层中的迁移，可概化为瞬时注入示踪剂(平面瞬时点源)的一维稳定流动二维水动力弥散问题，污染物浓度分布模型如下：

式中：x，y：计算点处的位置坐标；t：时间(d)；C(x，y，t)：t时刻点x，y处的示踪剂浓度(g/L)；M：含水层的厚度(m)；mM：瞬时注入的示踪剂质量(kg)；u：水流速度(m/d)；n：有效孔隙度(无量纲)；DL：纵向x方向的弥散系数(m2/d)；DT：横向y方向的弥散系数(m2/d)；π：圆周率。

模型需要的主要参数包括：含水层厚度M=17.8 m；外泄污染物质量mM=680.4 g；岩层的有效孔隙度n=0.07；渗透系数K=0.13 m/d；地下水水力坡度I=1‰；水流速度u=0.001 86 m/d；污染物纵向弥散系数DL=0.011 5 m2/d；污染物横向弥散系数DT=0.004 6 m2/d，这些参数可以由研究区水文地质勘察及类比区域收集成果资料来获得，计算经过不在此处赘述。

3.2 预测结果

同样选取石油类作为预测因子，石油类的标准限值参照《地表水环境质量标准》(GB3838—2002)中的Ⅲ类标准。预测结果及向地下水下游方向最大超标距离图见表3及图4。

表3 地下水中石油类迁移距离预测结果表(解析法)

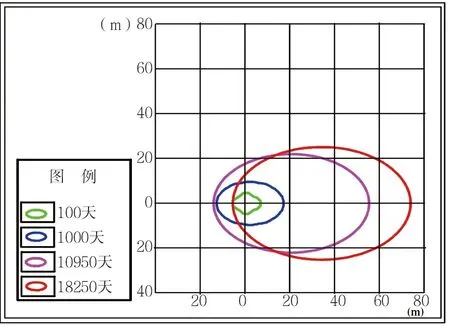
图4 地下水中石油类在不同时间污染晕运移图(解析法)

4 不同预测方法的预测结果对比分析

根据预测结果，对于解析法，污染物向地下水下游扩散最大超标范围呈规则的椭圆形，而数值法则呈不规则椭圆形，主要是因为解析法中假定地下水为均匀稳定流，而数值法可通过实际水位和计算水位的拟合分析，使二者的拟合效果基本趋于一致，从而使地下水流场基本符合地下水的实际运动特征[8]。

通过两种预测方法的结果比较，发现两个特点：(1)短时间内解析法预测结果小于数值法预测结果，达到最长预测年限50年时解析法预测结果超过数值法。(2)数值法在不同时间段内结果变化程度较解析法小。

针对特点(1)主要原因为：数值法模拟了污染物从地面下渗到含水层中然后再不断扩散这一整个过程。而解析法在等厚、均值、各项同性、无限长边界、稳定流边界的理想化条件下，在预测过程中假定污染物直接在含水层中注入，不考虑下渗过程，也不考虑土壤及微生物对部分污染物的吸附、降解作用，只考虑污染物在地下水流场作用下的对流弥散作用，故污染物在向下游运移的过程中，较数值模拟方法在纵向扩散的速率更快，污染物的运移距离更远[9]。但在短时间内污染物传播距离远的特点难以体现。

针对特点(2)主要原因为：在数值模拟过程中设定了实际的边界条件并将预测区域按照单元格进行拆分，模拟情况更接近污染物实际运移，污染物的运移速率整体缓慢，随着时间推移垂向上深度越大预测结果较解析法相比越小，不同时间段内污染物运移距离变化程度不如解析法的变化程度大。

鉴于本项目预测区域内水力参数各项异性、水流流场在厂区内也不能保持完全均一性，导致解析法对实际反映的准确性稍差。同时本项目工程运营时间较长(最长时间50年)，预测时间跨度较大也导致解析法运移距离变化较大。所以针对本项目解析法计算精度较数值法来看仍不太理想。但是各种预测方法都有其各自的适用范围。解析法作为地下水溶质运移预测方法的一种，为地下水污染预测提供了一种途径，为相关类似建设项目在地下水环境影响评价中的具体应用提供了科学依据，丰富了地下水环境影响评价方式，对及时做好地下水污染防治工作提供了一定依据。