高速磁浮列车气动声学特征的数值模拟研究

2022-11-25张洁吴雨薇高建勇高广军杨志刚

中南大学学报（自然科学版） 2022年10期

张洁，吴雨薇，高建勇，高广军，杨志刚

(1.中南大学交通运输工程学院，轨道交通安全教育部重点实验室，湖南长沙，410075；2.轨道交通安全关键技术国际合作联合实验室，湖南长沙，410075；3.轨道交通列车安全保障技术国家地方联合工程研究中心，湖南长沙，410075)

磁浮列车运行时悬浮于轨道之上，避免了轮轨系统的复杂接触，相较于高速列车能获得更高的速度，在安全、环保及能耗等方面优势明显[1-2]。600 km/h速度级高速磁浮列车被视为高铁和飞机之间的空白速度区的有效补充，具有广阔的发展前景，对完善高速交通运输体系具有重要意义[3]。但磁浮列车高速运行时，气动噪声强度剧增，不仅影响乘客的舒适性，而且对周边居民的正常生活会产生极大的影响[4]，因此，有必要对磁浮列车气动噪声进行研究。目前国内外对高速列车气动噪声的研究相对成熟。研究表明，高速列车气动噪声主要由车身外形不平整引起气流扰动所致，受电弓、风挡空腔、转向架是主要气动噪声源。ZHANG等[5]利用LES(大涡模拟)及FW-H声类比方法对受电弓气动噪声特性进行了数值仿真，发现弓头、底架及臂杆铰接处为主要声源，涡结构脱落及受电弓周围的流动分离是该区域气动噪声产生的关键因素。黄莎等[6]采用大涡模拟与声类比相结合的方法，对高速列车连接部位气动噪声展开研究，发现该区域噪声呈宽频特性，声能量主要集中在低频。LIANG 等[7]基于大涡模拟及Ffowcs Williams-Hawkins 声学模拟方法对头车1 位转向架气动噪声产生机理进行研究，发现空腔噪声为该区域主要发声源。何娇等[8]对3 车动车组模型在200，250，300及350 km/h速度级下气动噪声特性进行仿真模拟，发现列车偶极子声源强度主要分布在转向架及其周围的车体表面位置，头车流线型附近辐射声压级较大。谭晓明等[9]对CIT500 高速列车在200～350 km/h 区间内列车辐射噪声声源特征进行研究，发现转向架、受电弓、车头、风挡均为列车噪声源区，其中，转向架及受电弓为最主要的噪声源，这与ZHANG等[10]利用声阵列技术对310 km/h 速度级下高速列车车外辐射噪声源位置的研究结果一致。THOMPSON 等[11]认为在300～350 km/h 速度区间内，列车气动噪声主要由气流流经受电弓、车头、转向架等不平顺区域产生。相较于高速列车其他噪声源，车体表面湍流边界层产生的气动噪声不占主导地位，但在更高速度级下，其影响将更为显著。

与高速列车相比，磁浮列车车体表面光顺，无转向架、受电弓等复杂结构，车体表面边界层内气流扰动发展及尾部诱导分离现象不容忽视，且磁浮列车最高运行速度可达到600 km/h，四极子噪声贡献凸显。目前，人们对高速磁浮列车气动噪声的研究很少，仅开展了上海TR08磁浮列车400 km/h及以下速度级的试验研究[12-14]，因此，有必要对适用于高速磁浮列车气动噪声仿真方法进行研究。本文基于K-FWH 方程及大涡模拟方法[5,7-8,15]，通过对比400 km/h速度级下高速列车与磁浮列车气动激扰特征及声场特性，分析磁浮列车发声机理；从头、中、尾三部分扰动源特征出发，讨论不同区域积分面设置，对600 km/h 速度级下高速磁浮列车偶极子、四极子气动辐射噪声进行仿真研究。

1 数学物理模型

1.1 大涡模拟

大涡模拟控制方程为空间隐式滤波N-S 方程[15]，其中，空间滤波器由特征宽度决定(Δi(i=1,2,3)分别为x，y和z这3个方向的计算网格边长)。

滤波后的动量方程及连续性方程为：

式中：t为时间；ρ为气体密度；μ为黏性系数；xi为直角坐标系分量；和为滤波后的速度分量；为滤波后的压力；τij为亚格子应力，为求解其中的未知量，需对亚格子应力进行建模，本文采用Smagorinsky 亚格子模型[16]，其应力表达式为

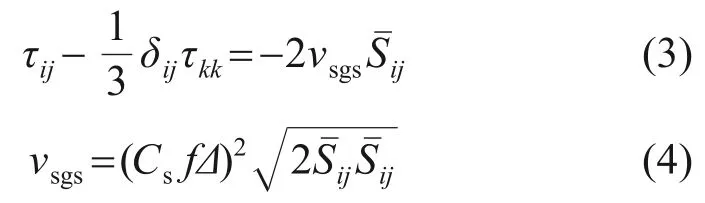
式中：δij为克罗内克函数；τkk为亚格子应力各向同性部分；为流体微团的应变率；vsgs为亚格子尺度的黏度，Cs为Smarorinsky 常数，Cs=0.1；f为Van Driest 阻尼函数。

1.2 可穿透积分面声辐射方法

FRANCESCANTONIO[18]在传统FW-H 方程基础上利用KIRCHHOFF[19]提出的方法，推导得到了应用范围更广的 K-FWH(Kirchhoff-Ffowcs Williams-Hawkings)方程[20]：

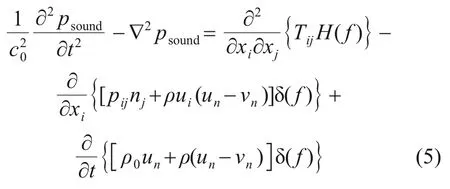
2 数值计算模型

采用1∶8缩比的磁浮列车模型及高速列车模型进行仿真计算。磁浮列车省去头、尾车顶部的无线电终端，以车高H=0.5 m 为特征长度，车长为20H，宽为0.9H，从上游至下游将车体划分为头车(流线型区域)、头车车身、中车车身、尾车车身和尾车(流线型区域)几部分，如图1(a)所示；高速列车保留转向架、风挡等重要部件，以车高h=0.5 m为特征长度，车长为20h，车宽为0.83h，如图1(b)所示。

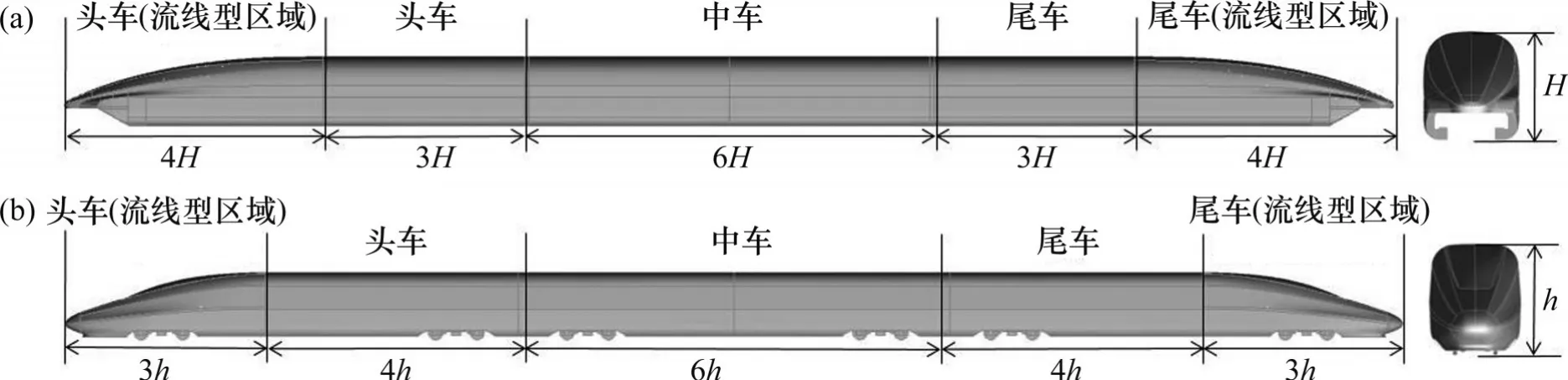
图1 列车模型Fig.1 Train models

图2(a)所示为磁浮列车计算域示意图，用于模拟磁悬浮列车在高架上的运营情况。列车及轨道位于计算域正中间，其中计算域入口ABCD和出口A1B1C1D1均采用压力远场边界条件，流域4个侧面均给定对称边界条件，使该面法向速度为0 m/s，保证流场发展的同时能消除壁面对流场的影响。磁浮列车模型表面设定为无滑移边界，轨道为滑移固壁边界条件，滑移速度与来流速度一致。图2(b)所示为高速列车计算域示意图，高速列车位于距离地面0.05h处。计算域入口、出口同样采用压力远场边界条件，地面DCC1D1设置为滑移固壁边界，滑移速度与来流速度一致。其余侧面均设置为对称边界，高速列车模型表面给定无滑移边界条件。

图2 计算域Fig.2 Computational domains

图3所示为磁浮列车及高速列车模型网格示意图。磁浮列车和高速列车流线型车头均采用边长为3.75 mm 的网格，头车尾车采用边长为5 mm 的网格，中车采用边长为6.25 mm网格，其中，高速列车风挡网格边长为6.25 mm，转向架网格尺寸为5 mm。为精确描述表面偶极子气动噪声源，在磁浮列车及高速列车车体表面增设15 层附面层，采用三棱柱网格覆盖，第一层网格厚度为0.012 5 mm，增长系数为1.2。磁浮列车网格数为1.3 亿个左右，高速列车网格数为1.1亿个左右。划分600 km/h速度级下磁浮列车网格时，在磁浮列车尾部建立积分面，积分面内最大网格边长设置为12.5 mm，其余网格边长设置保持不变，网格数为2.1 亿个左右。各个工况列车表面第一层网格所对应的y+值均在1以下，表明网格边长能够满足大涡模拟基本要求。

图3 计算网格Fig.3 Computational grids

采用商业CFD 软件ANSYS Fluent 进行数值仿真计算。考虑到来流马赫数大于0.3，空气可压效应明显，因此，稳态流场计算选取基于密度基的隐式求解方法，采用SSTk-ω湍流模型开展数值仿真，对流项和耗散项均采用二阶迎风格式进行离散。随后，开展大涡模拟(LES)计算，采用基于Smagorinsky-Lilly的LES模型，压力和速度场耦合采用Coupled算法进行计算；采用有界二阶隐式格式对时间导数进行离散，有界中心差分用于求解动量方程。非定常计算时间步长为5×10-5s，每时间步长内迭代30 次，共计算10 000 个时间步，确保气流有足够的时间通过整个计算域，并通过监测车辆气动力以及距离车尾1个车长位置处的速度变化，判断流场是否达到充分发展程度。

3 声学风洞验证

在中国空气动力研究与发展中心的声学风洞中进行磁浮列车气动噪声测试。试验模型为某型高速磁浮列车3车编组1∶8缩比模型(见图4)，模型高为H1，宽为0.94H1，长为19.7H1，试验来流速度为300 km/h。为研究试验模型的远场噪声辐射特性，在模型侧面布置16 个远场传声器。远场传声器布置如图5所示。沿垂向共布置2排，第一排传声器距离地板0.8H1，第二排距离地面1.6H1；每排沿轴向(X向)布置8个，轴向间距为1.6H1，上游第一个传声器距车头3.2H1。试验中，所有传声器通道进行同步采集，采样频率为51.2 kHz，采样时间为90 s。

图4 风洞试验模型Fig.4 Wind tunnel test model

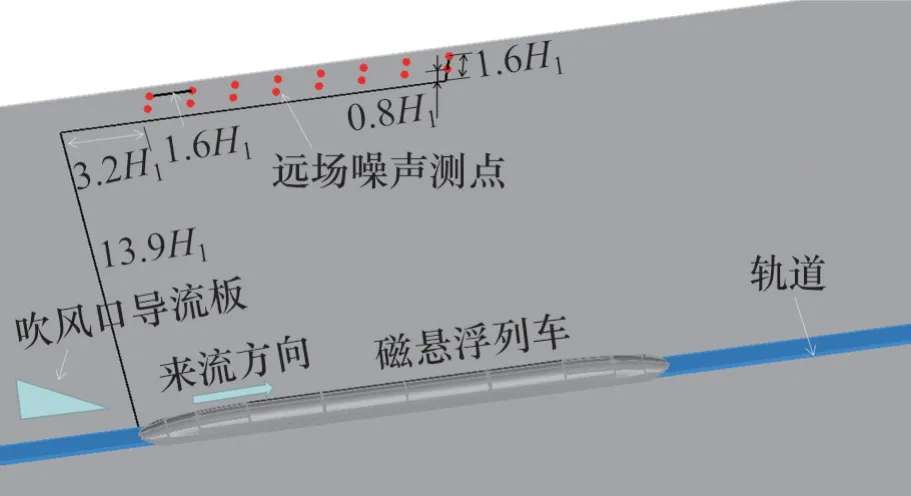
图5 传声器布置图Fig.5 Arrangement of microphones

按照风洞试验模型建立对应数值仿真模型，并在相应位置建立声压级测点。表1所示为风洞试验结果和数值仿真结果。

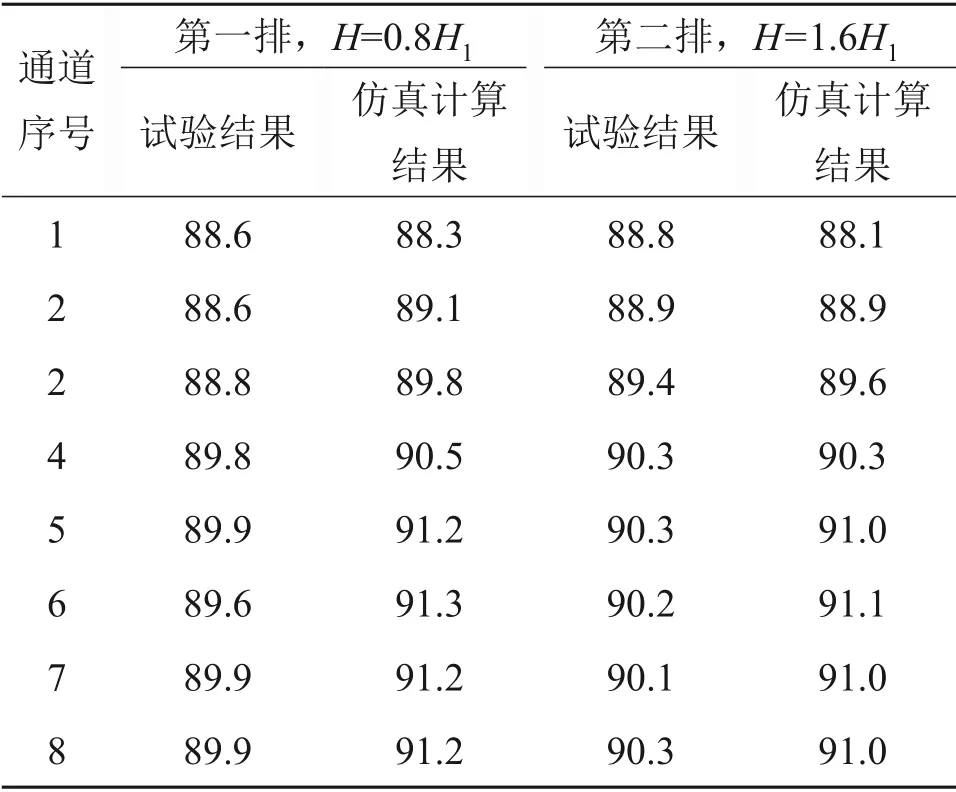
表1 300 km/h时仿真和试验辐射噪声对比Table 1 Comparison of radiated noise between simulation and test at 300 km/h dB

在距离地面高度为0.8H1测点位置，磁浮列车辐射噪声仿真结果和试验结果的误差最大为1.7 dB；在距离地面高度为1.6H1测点位置，仿真结果和试验结果的误差在0.9 dB以内。可见，本文采用的仿真模型具有较高精度。

4 气动激扰发声研究

国内外在高速轮轨列车气动噪声特征方面已有较多研究成果，但高速磁浮列车在气动外形上与高速轮轨列车存在显著差异。为明确新型磁浮列车与现有高速列车气动噪声的差异性及磁浮列车气动激扰发声机理，从气动激扰特征、噪声源分布以及远场辐射噪声这3个方面对400 km/h速度级的磁浮列车和高速列车气动声学特征进行对比分析，以便为高速磁浮列车气动噪声研究方法提供支撑。

4.1 气动激扰特征

由于空气的黏性作用，当气流流经固体表面时，会形成具有较大速度梯度的附面层，其厚度定义为壁面法向方向上速度为0.99Uin时的垂直距离(其中，Uin为来流速度)。图6所示为高速列车和磁浮列车周围瞬时附面层云图，利用式(6)对速度进行无量纲化处理。

图6 附面层云图Fig.6 Boundary layer contours

由图6(a)可知：气流撞击磁浮列车鼻尖点时，速度迅速下降，在该位置形成滞止区，随后气流沿车身向后运动，附面层稳定发展，厚度沿车身不断增加；在气流流经尾车流线型肩部后，由于车身曲面变化，气流与车体分离，在该区域形成湍流度较高的回流区，在不同低速区呈嵌套式分布；在列车与轨道之间的腔体区域，气流撞击头车鼻尖点后沿着鼻尖点两侧进入底部空间，随后气流速度沿流向不断减小。由图6(b)可见：高速列车车体上方流场特征与磁浮列车的相似。在头车流线型区域，高速列车气流稳定位置相对靠后，在尾车流线型区域，高速列车附面层分离点相对提前；在车体下方，气流在流经转向架等复杂结构时，引起大尺度扰动，并向车体两侧扩散。

为展示列车周围瞬态流场结构，采用Q准则来识别列车周围的涡结构。Q准则表达式如下：

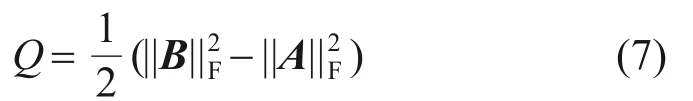
式中：B和A分别为速度梯度张量的反对称项和对称项，即旋转涡量幅值和剪切应变张量幅值。

图7 所示为磁浮列车和高速列车Q等值面云图。由图7(a)可见磁浮列车涡结构主要集中在头车流线型及尾车流线型区域。在头车流线型产生的涡结构主要可分为3种类型：1) 在头车流线型顶部形成周期性的小尺度涡结构，此处涡结构聚集呈条纹状分布，直至肩部消失；2) 在头车流线型两侧车身与抱轨之间的过渡区域，涡结构呈条状分布；3) 在头车流线型抱轨底部，高速气流冲击抱轨后，部分气流流向抱轨与轨道中间的狭窄缝隙，另一部分沿着抱轨底面发展，并在该区域形成周期性脱落的蠕状涡结构。尾车流线型上表面涡结构分布特征与头车流线型的分布特征类似，但其速度幅值远小于头车流线型涡结构的速度幅值。在尾车流线型两侧，气流沿着车体表面向下游发展，形成一系列小尺度涡，涡团聚集成带状结构。列车尾流区受附面层内气流分离再附着的影响，表现出明显的气流掺混特征，在轨道两侧形成类似于卡门涡街的对称涡结构，继续向下游发展。

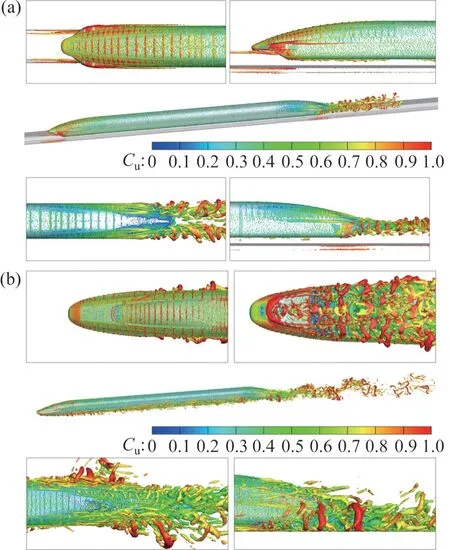
图7 Q=200 000时的列车周围涡结构Fig.7 Vortex structures around trains when Q=200 000

从图7(b)可知：高速列车头、尾车流线型区域出现与磁浮列车类似的条状涡结构分布，在头车车窗位置产生小尺度涡，沿气流向后发展成长条状；在尾车流线型区域，流体分离及气流掺混效应显著，形成尺度丰富的涡结构；在涡结构向后运动的过程中，速度不断增加；在列车底部排障器边缘，气流发生分离，形成涡包，在向下游发展过程中形成螺旋状涡结构。在转向架区域，以头车1位转向架为例，转向架舱前沿分离的剪切流与转向架轮对及转向架舱后壁相互作用，在地面与转向架之间产生大尺度涡结构，并从两侧溢出沿车体侧壁向后发展，涡结构尺寸进一步增大；其余转向架区域流场结构与1位转向架区域的流场结构类似，但气流脉动程度较弱。

4.2 偶极子噪声源

列车表面脉动压力时间梯度均方根归一化可表征列车表面偶极子声源强度，计算公式如下(其中，利用式(9)进行量纲归一化处理)：

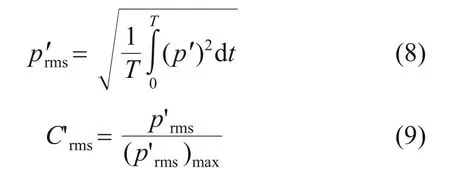
式中：C'rms为归一化的列车表面偶极子声源强度。

图8 所示分别为磁浮列车以及高速列车表面C′rms云图。由图8可见：在同一速度级下，高速列车车体表面偶极子声源分布范围明显比磁浮列车的大。其中，磁浮列车偶极子声源主要分布在头车流线型鼻尖底部区域、头车流线型抱轨底部、尾车流线型鼻尖及其底部区域范围；高速列车偶极子声源主要分布在头车迎风玻璃凹陷处、转向架区域、转向架舱导边后方区域以及尾车流线型区域，头车1 位转向架(#1)区域的偶极子声源强度最大。

图8 列车表面C′rms云图Fig.8 C′rms contours on train surface

为确定列车各部分对整车偶极子声能量贡献占比，利用式(10)计算得到各个部件等效声源声功率，进而得到各部件偶极子声源能量占比。

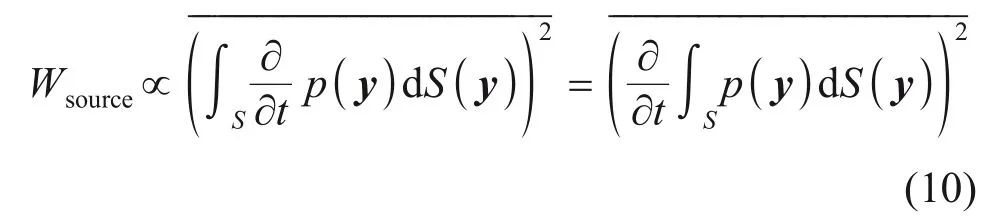
其中：Wsource为声源等效声功率；y为声源空间坐标矢量；为列车表面脉动压力时间梯度；S为噪声源面积。各部件等效声源声功率占比计算结果如图9所示。从图9可见：磁浮列车各部件偶极子声源能量占比呈两头大、中间小的分布特征，其中尾车(流线型区域)声源能量最大，占比为34.9%，其次为头车(流线型区域)；高速列车各部件偶极子声源能量占比总体上呈沿车身减小的趋势，头车(流线型区域)占比最高，为29.8%，尾车(流线型区域)占比最低，中车由于车体面积较大，声源能量占比比头、尾车的高。

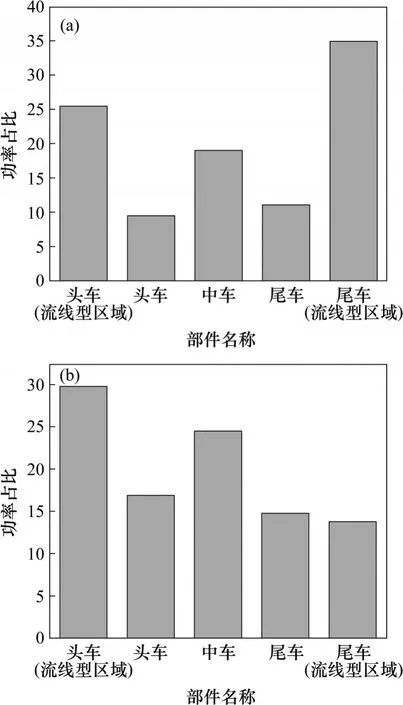
图9 各部件等效声源功率占比Fig.9 Proportion of sound power of equivalent sound source of each component

4.3 远场噪声辐射特性

A计权是一种常用的噪声评价指标，用于反映人耳的响应特性，用dB(A)表示。为考察列车远场噪声辐射特征，在距离高速列车及磁浮列车纵向对称面6.25H远至离地面0.875H高之处，每隔2.5H布置1个测点，测点1与头车鼻尖点齐平。具体测点布置如图10所示。

图10 远场测点布置示意图Fig.10 Layout diagram of far-field measuring points

图11 所示为磁浮列车和高速列车远场噪声声压级对比结果。由图11 可见：在400 km/h 速度级下，磁浮列车远场噪声远比高速列车的小，其中，高速列车各测点声压级分布整体呈下降趋势，声压级最大值分布在测点1，为102.4 dB(A)。测点5至测点7 的声压级有较小波动；与高速列车不同，磁浮列车测点声压级呈先上升后略微下降趋势，在测点6 达到最大值，为79.5 dB(A)。在同一速度级下，磁浮列车的远场辐射声能量集中分布于列车尾部，而高速列车头部声能量更明显，可见磁浮列车与高速轮轨列车流场结构及气动发声机理存在较大差异。高速轮轨列车车身不平顺，气流在流经转向架等复杂结构时，气动激扰强烈，产生较多声源，而磁浮列车车身平顺，尾车流线型区域曲面变化导致的附面层分离是磁浮列车发声的主要原因。因此，在对磁浮列车气动噪声开展进一步研究时，应着重关注尾车流线型区域的附面层发展以及尾流区域的空间扰动。

图11 远场辐射声压级Fig.11 Sound pressure levels of radiated noise

5 600 km/h 速度级磁浮列车远场噪声研究

磁浮列车与高速列车气动激扰发声对比分析结果明确了磁浮列车偶极子噪声源特征。据文献[23]，当磁浮列车运行速度提升至600 km/h 时，马赫数接近0.5，气动激扰剧烈，四极子声源能量不容忽视，这对更高速磁浮列车气动噪声仿真方法提出了新的要求。因此，基于前面对磁浮列车气动噪声的研究，针对磁浮列车发声特性，考虑空间四极子噪声影响，这里采用可穿透积分面并结合KFW-H 方程对600 km/h 速度级磁浮列车气动噪声进行仿真计算，同时对比不设积分面以车体作为声源面进行积分计算的结果，以验证空间四极子噪声源对磁浮列车辐射和噪声的影响。

原则上，建立包裹整个列车的穿透积分面且外推得够远，就能完全捕捉列车周围声源扰动，从物理上可避免声源能量的缺失。但此方法会使得网格量急剧上升，影响计算效率，且网格滤波效应可能导致计算车体表面偶极子源辐射时产生较大误差[22]。为保证模型的计算精度，本文仅在可能形成四极子声源区域建立穿透积分面。在四极子声源产生区域，通常伴随着较强的涡脱落现象[24]。对磁浮列车流场结构进行分析可知，磁浮列车在头车流线型区域存在少量涡结构脱落，尾车流线型因附面层分离引起的空间扰动强烈，因此，这里仅考虑在头车流线型、尾车流线型区域建立可穿透积分面。构建积分面时，尽可能使其包含列车主要声源区域，同时确保积分面不产生“伪源”[25]。

图12 所示为600 km/h 速度级磁浮列车尾流区流向涡量发展规律。由图12 可见：尾流区涡量在160 m下游波动趋于平稳，且涡量幅值低于100 s-1。根据尾流区涡量发展规律建立穿透积分面，如图13 所示。从图13 可见：穿透积分面起于尾车流线型肩部位置，总长为24H，尾端面A1B1C1D1对应x坐标为160 m；底面CDD1C1距离轨道底部约0.25H，顶面ABGH距离车顶约0.25H，总高约为2H。由于尾流区的涡结构往后发展的过程中向两侧发散，因此，穿透积分面采用上游小、下游大的形式。积分面前端面ABCD宽度为2H，尾端面A1B1C1D1宽度为3.5H。由于积分面后端面A1B1C1D1位于尾流区，可能存在质量穿透产生伪声，且尾部积分面延伸得足够远，四周积分面足以捕捉该区域声源信息，因此，在计算远场辐射噪声时，不对后端面进行积分。

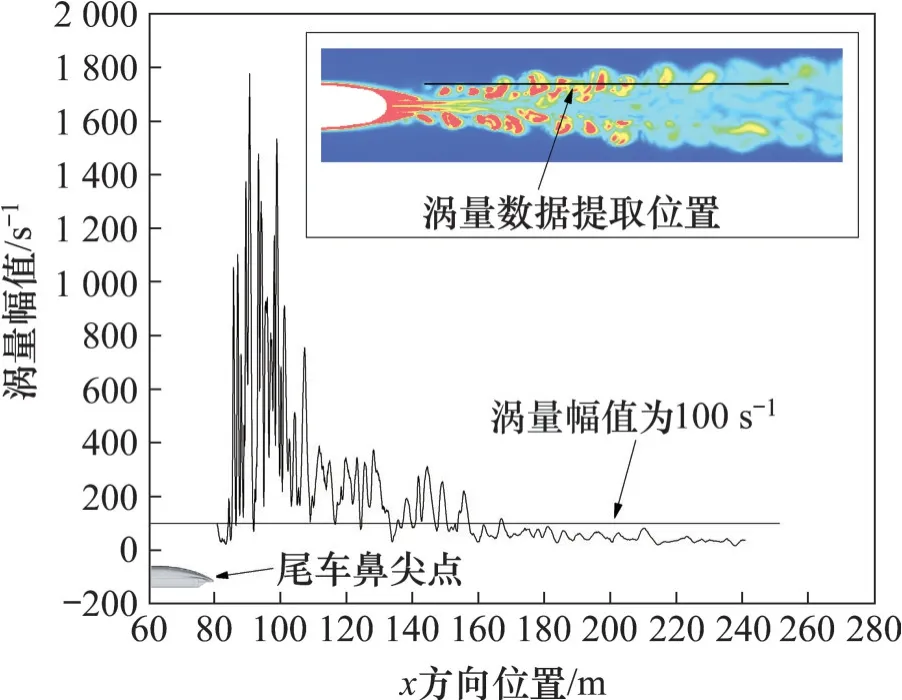
图12 尾流区涡量发展示意图(y=1.6 m，z=1.2 m)Fig.12 Diagram of vorticity development in wake region(y=1.6 m,z=1.2 m)

图13 尾车流线型积分面Fig.13 Integral surface around streamlined head of tail car

利用远场测点对不同积分方案远场辐射噪声进行研究，测点位置与前面的一致，计算结果如图14 所示(其中，方案1 不设积分面，以车体作为声源面，进行积分计算；方案2在尾车流线型区域建立积分面，积分计算时，有积分面包裹区域以积分面作为声源面，无积分面包裹区域仍以车体作为声源面)。由图14可见：在建立积分面后，各个测点的声压级均增大，表明积分面有效捕捉到尾车流线型区域四极子声源，测点越靠近尾流区，增大越明显；测点9 声压级增长幅值最大，为4.9 dB(A)。

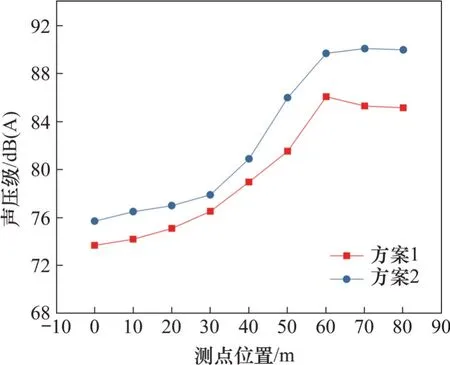
图14 辐射噪声声压级Fig.14 Sound pressure levels of radiated noise

测点7为车体辐射噪声峰值测点，取该测点的频谱曲线对列车远场辐射噪声频谱特性进行分析，结果如图15所示。由图15可见车体辐射声能量呈宽频特性，在尾车建立积分面后，测点低频能量明显增加，表明尾流区四极子噪声能量主要分布于低频段，测点高频段能量有所损失，有可能是网格的滤波效应所致。

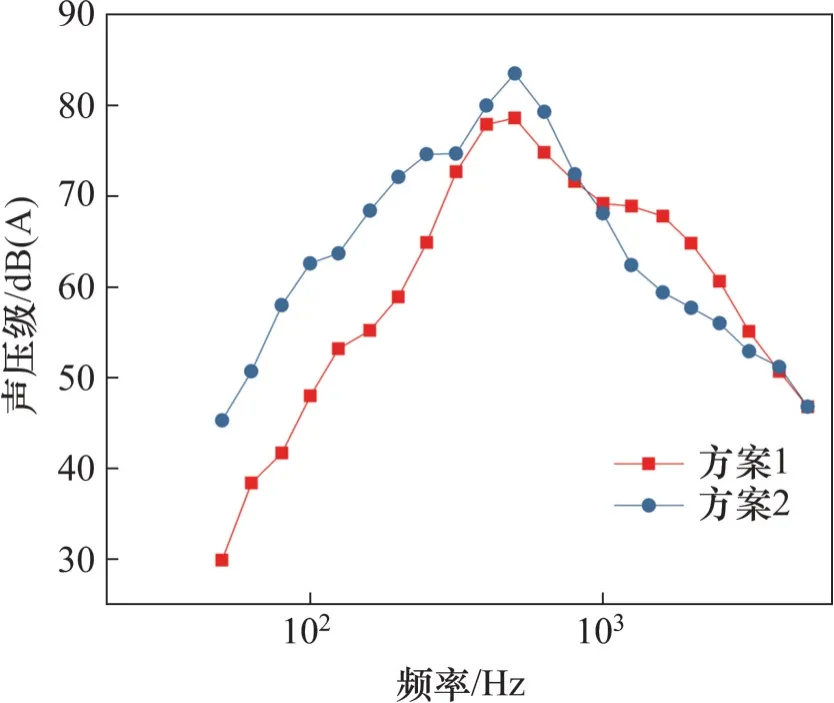
图15 测点7的辐射噪声频谱曲线Fig.15 Spectrum curves of radiated noise for point 7

在尾车流线型积分面基础上，对头车流线型区域积分面进行研究。头车流线型积分面如图16所示，前端位于鼻尖点前1.25H处，在头车流线型肩部位置截断，长为5.2H，宽为2H，高为2H。

图16 头车流线型积分面Fig.16 Integral surface around the streamlined head of the head car

图17 所示为建立积分面后远场噪声辐射结果与车体辐射结果的对比结果，其中方案1、方案2工况不变，方案3在方案2的基础上设置头车流线型积分面。由图17可见：方案3和方案2的远场辐射结果相近，各个测点的差值在0.3 dB(A)以内，表明头车附近几乎没有四极子声源，无需在头车建立穿透积分面。

图17 辐射噪声声压级Fig.17 Sound pressure levels of radiated noise

综上可知，当磁浮列车高速运行时，四极子声源主要分布在尾车流线型及其尾流区域，在研究磁浮列车气动噪声时，只需在该部分建立可穿透积分面。

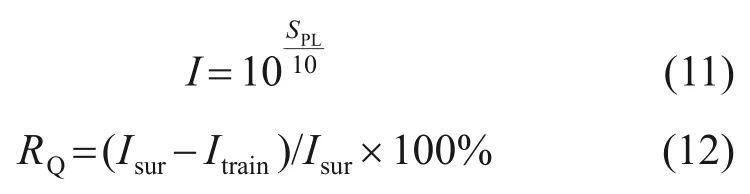
式中：RQ为四极子辐射声能量占比；I为辐射声能量；SPL为测点声压级；Isur为建立积分后远场辐射声能量；Itrain为无积分面时远场测点辐射声能量。

由式(11)和(12)可计算得到测点9 四极子辐射声能量占比及测点1至测点9的四极子辐射声能量占比平均值，分别为56.3%和60.9%。可见，该速度级下四极子声源辐射能量较强，对远场辐射噪声的贡献超过偶极子声源的贡献。

为研究列车远场辐射噪声指向性，在xOy，yOz和xOz这3 个平面，以头车鼻尖点为圆心，分别建立半径为500 m的圆，在各个圆周上均匀布置36个测点，如图18所示。图19所示为各个测点辐射噪声计算结果，其中，从最里面的圈到最外面的圈是从25 dB(A)到55 dB(A)等比例分配的。

图18 指向性测点布置示意图Fig.18 Layout diagram of directivity measuring point

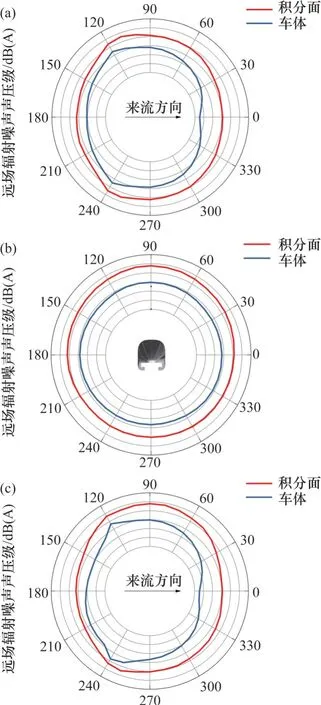
图19 噪声辐射指向性示意图Fig.19 Diagrams of radiated noise directivity

由图19 可见：列车车体噪声在yOz平面，指向性呈圆形，表现出点声源特征，各个方向的辐射噪声差异较小；在xOy及xOz两平面指向性特征相似，均在“8”字形基础上产生少许变化，表现出偶极子声源特性，噪声主要辐射方向为斜前方，峰值均分布120°及240°方向；设置积分面后，在xOy面，各个方向的噪声辐射均增大，指向性无明显变化；在xOy及xOz两平面，列车尾部辐射噪声增长明显，峰值位置均向列车后方偏移；在xOy平面，峰值位置偏转10°左右；在xOz平面，峰值位置偏转约30°。