单轴压缩过程中岩石的实时超声波特性
2022-11-25贾蓬祝鹏程李博徐雪桐
贾蓬,祝鹏程,李博,徐雪桐
(东北大学 资源与土木工程学院,辽宁 沈阳,110819)
我国矿山工程、岩土工程等目前正处于快速发展时期,能源开发难度日益增大、工程地质条件日趋复杂、工程建设体量逐年攀升所带来的诸多岩石力学问题成为众多学者关注的热点[1-5]。超声波作为一种重要的无损检测手段,因其穿透力强、操作简单、可靠性高和安全性好等优点,被广泛应用于岩石力学工程领域。由于岩石在外力作用下的内部损伤演化会引起声学参数的改变,超声波测试常被用于岩石的完整性检测,因此深入研究岩石在加载过程中的声学参数演化规律对指导工程建设及岩土工程地质灾害预防预测具有重要意义[6-8]。
弹性波在岩石内部传播时,遇到孔隙、裂隙和层理结构等会产生散射、绕射现象,因此岩石声学参数的变化可以表征其力学性质与内部结构变化,进而评价岩石的损伤程度。REZAEI 等[9]在实验室研究了干燥和饱和岩石纵波波速与单轴抗压强度、弹性模量、密度、泊松比、吸水率等物理力学参数之间的关系。SAROGLOU 等[10]研究了压裂程度对岩石中P波和S波速度的影响,发现波速随压裂程度增加而呈指数下降。HEMMATI等[11]利用超声波纵波指数对岩体参数进行分类和评估,发现不连续面的粗糙度越大,岩体中纵波波速越低。JIA等[12]利用纵波波速及频谱分析并结合实时电阻率,研究了加载过程中饱和砂岩的内部裂纹发展状况。徐晓炼等[13]研究了超声波波速与煤岩密度、渗透率、孔隙度、层理的关系。张天军等[14]研究了含水率对含孔试件单轴压缩破坏过程中超声波声学特性的影响。罗津辉等[15]通过分析加载过程中纵、横波速和振幅的变化,将岩石破坏过程分成几个阶段,进而预测岩石破裂。赵明阶等[16-17]建立了受载条件下岩石的声学特性模型与损伤演化模型,并将岩石在未受荷载条件下的纵波波速定义为初始损伤变量。郑贵平等[18]研究了不同岩石波速随应力变化的响应规律。张培源等[19]用Hooke介质模型建立了岩石弹性模量与弹性波速的关系。胡明明等[20]研究了砂岩在单轴压缩过程中3 个不同方向纵波波速与应力的演化规律。李浩然等[21]对单轴压缩过程中盐岩声波活动规律进行研究,发现纵、横波波速随应力呈上升—平稳—下降趋势。施行觉等[22]通过试验发现在98%破裂强度时岩石纵波波速最大,然后逐渐下降直至破裂,认为这是由于临近破裂,膨胀作用大于压缩作用,密度降低导致波速下降。
上述研究成果对于利用超声波声学参数判定岩石损伤的研究具有重要参考价值。但以往的研究多是针对纵波波速,且是加载或受力过程中某一时刻的波速,并未对岩石在受力过程中的实时纵波和横波波速变化特征开展研究,有关岩石损伤破裂过程的实时声学特性及其与损伤破裂过程的内在联系的研究还较少。鉴于此,本文以花岗岩、红砂岩和大理岩三类工程中常见的岩石为研究对象,分析不同种类岩石在加载过程中的实时纵、横波声学参数与岩石损伤破裂过程及力学参数变化的相互关系,以期为利用岩石的声学参数预测岩石的应力和损伤状况提供理论依据。
1 岩石的物理力学参数
分别选取辽宁凌海市白台子乡李家店村花岗岩、山东临沂莒南县红砂岩和山东省莱州市夏邱镇大理岩三类岩石,根据国际岩石力学学会(ISRM)所提标准岩样规格,制备直径为50 mm、高度为100 mm 的圆柱体,两端平整度及垂直度误差不超过0.2 mm(图1)。为减小岩石试件的离散性,相同岩性的岩石试件均取自同一块完整大块岩石,并利用湘潭市天鸿研究所生产的HS-YS403B 型岩石声波参数测试仪进行初始纵、横波波速测试,每类岩石均选取波速接近的岩石试件进行试验。三类岩石的基本物理力学参数见表1。

图1 岩石试件Fig.1 Rock specimen
从表1可以看出,在自然条件下,三类岩样中大理岩平均孔隙率最小,密度最大,致密程度最高,平均纵波波速为3 901 m/s,平均横波波速约2 449 m/s,平均抗压强度为130.83 MPa;红砂岩平均孔隙率最大,密度最小,致密程度最低,平均纵波波速为2 195 m/s,平均横波波速为1 266 m/s,平均抗压强度约34.06 MPa;花岗岩平均孔隙率、密度介于两者之间,但其抗压强度与纵、横波波速最大。这表明岩石声波速度不仅取决于其孔隙度和密度,还与岩石的强度、岩性有较大关系,这与文献[23]中的结论是一致的。

表1 岩样的物理力学参数Table 1 Physical and mechanical parameters of rock samples
2 实时超声波测试方案与加载过程
每类岩石选取3个试件开展试验,试件上下两端放置超声波承压换能器,并涂抹凡士林耦合剂以保证良好接触。利用HS-YS403B型岩石声波参数测试仪对岩石加载过程中P波、S1波、S2波参数进行实时采集,每隔5 s 采集一次数据。采用吉林省金力试验技术有限公司生产的岩石刚度试验机(最大工作压力为3 000 kN),以加载速率为0.002 mm/s的位移控制方式对岩样进行单轴压缩,每隔1 s 采集一次数据,同步声波与应力采集时间,直至试件破坏。加载及超声波采集系统如图2所示。

图2 加载及超声波采集系统Fig.2 Loading and ultrasonic wave acquisition system
HS-YS403B 型岩石声波参数测试仪有上下承压三分量换能器(型号TH-CY260G08),换能器可发射1个纵波(P波)、2个横波(S1波、S2波),S1波工作方向为出线接口方向,S2波工作方向与S1波工作方向垂直。试验时,发射换能器发射电脉冲激励晶片振动,发射出声波在岩石中传播,后经接收换能器接收,将声能转换成微弱的电信号至接收系统,经信号放大、模数转换后在屏幕上显示波形,如图3所示。波速计算公式为v=l/Δt,Δt=t1-t0,其中v为纵、横波波速,m/s;l为试件长度,m;t0为校零时间,μs;t1为纵、横波初至时间,μs;Δt为测试岩样声波走时,μs。为了便于分析数据,依次选取5%~100%σc(增量为5%σc,其中σc为峰值应力)处的声波信号与其对应的应力和应变。
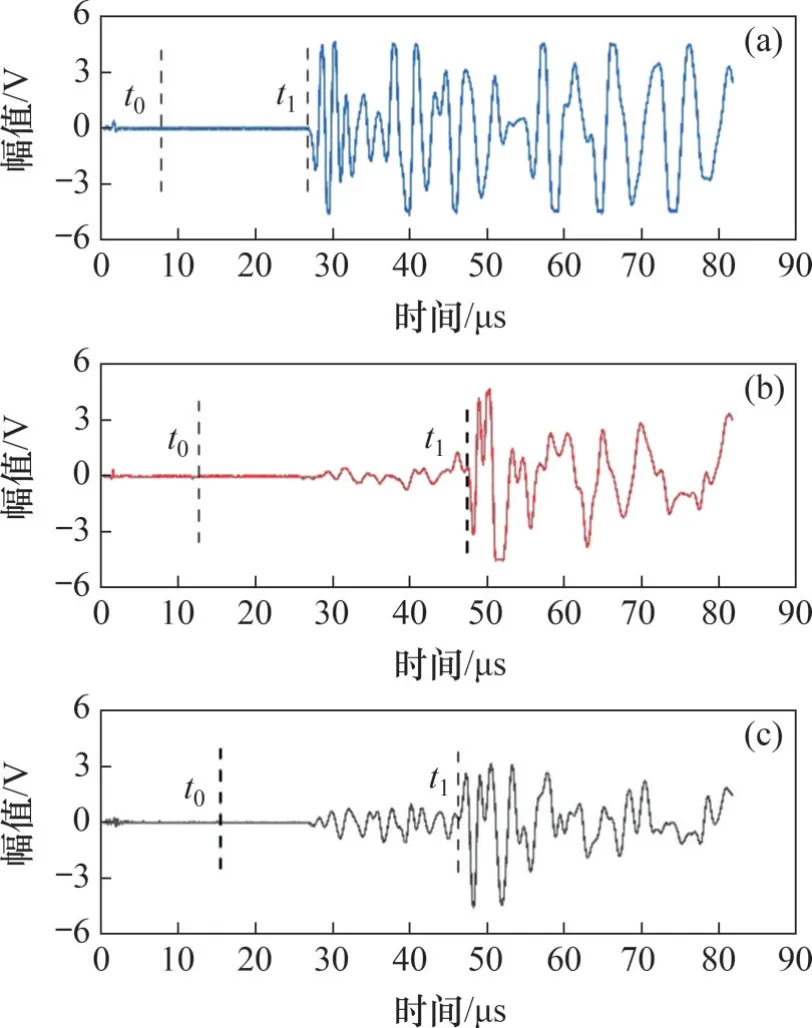
图3 声波波形Fig.3 Acoustic wave forms
3 试验结果与讨论
3.1 压缩过程中岩石的实时纵、横波波速变化规律
图4所示为不同类型岩石在加载过程中的平均波速与应力-轴向应变曲线的关系,表2 所示为不同加载阶段纵、横波波速的增幅。波速变化与岩石损伤有明显相关性,与岩石内部裂纹的萌生、扩展和贯通阶段相对应,横波波速变化可分为如下3个阶段。

图4 压缩过程中波速实时变化曲线Fig.4 Real-time wave speed curve during compression
1) 快速上升阶段(Ⅰ)。三类岩石的实时纵、横波波速呈现快速的上升趋势,这是由于岩石内部原有的微裂隙在外力作用下逐步闭合,弹性模量增大,声波发生的折射、反射、散射现象减少,波速增大。从表2可以看出,纵波波速增幅大于横波波速增幅,这主要是岩石在纵向上被压密所致。
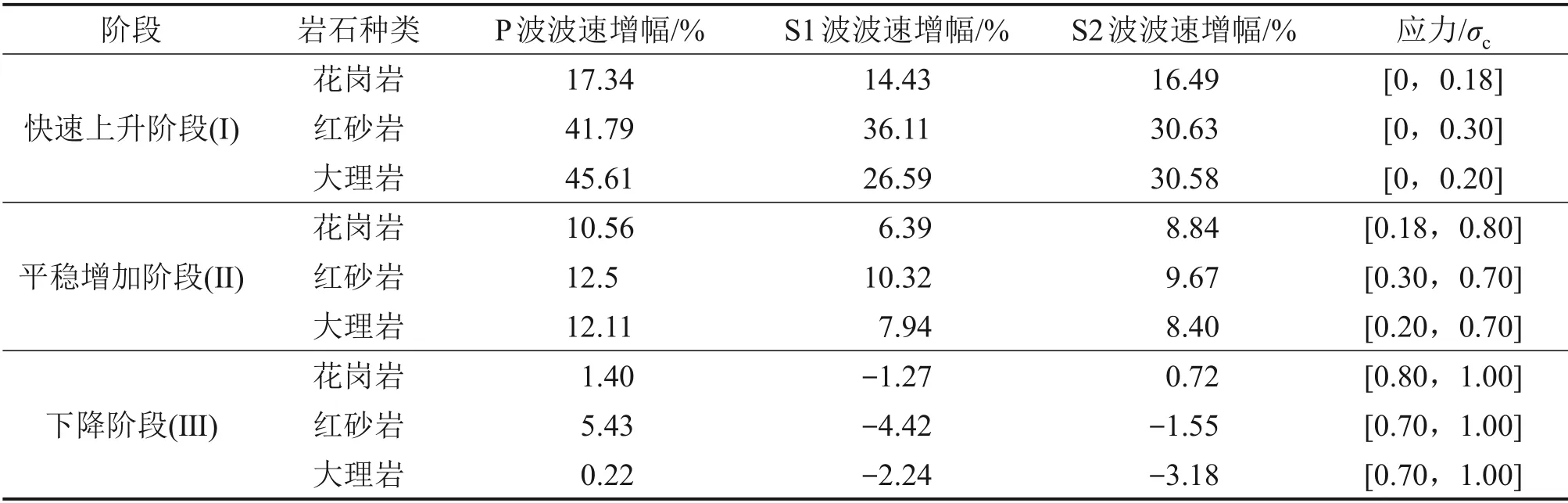
表2 各阶段岩石平均波速增幅Table 2 Rock wave average velocity increase amplitude at each stage
2) 平稳增加阶段(Ⅱ)。该阶段岩石应力-应变曲线基本呈直线状态,三类岩石的实时纵、横波速增幅较压密阶段逐渐减小。
3) 下降阶段(Ⅲ)。三类岩石的纵、横波波速增幅持续减小。实时横波波速比实时纵波波速先达到峰值点(70%~80%σc时,如表2 所示),其中红砂岩与大理岩的实时纵波波速的峰值明显滞后于实时横波波速的峰值,这说明针对所研究的岩石试样,实时横波波速峰值点可以作为岩石尤其是渐进性破坏特征明显的岩石破裂的前兆(红砂岩和大理岩的破坏表现出明显的渐进性特征,而花岗岩的破坏表现为突发性)。
3.2 实时纵、横波波速与岩石应力状态的关系
从图4可以看出,应力与纵、横波波速的关系呈指数函数趋势[20],分别对三类岩石应力与平均波速关系进行指数函数拟合,其表达式为

式中:y为应力;x为波速;系数a和b为拟合常数,其值取决于岩样类型与裂隙发育程度。
岩石应力-波速拟合结果如图5 所示。从图5可以看出,岩石试件实时纵波波速与应力的相关性强于实时横波波速与应力的相关性,三类岩石纵波采用指数函数拟合的相关系数均达到0.95 以上。花岗岩纵、横波速拟合效果最好,大理岩实时横波波速在80%峰值应力前的拟合相关系数大于0.91,红砂岩实时横波波速在75%峰值应力前的拟合相关系数大于0.97,表明指数函数更适合对刚性大的岩石进行拟合。因此,可通过室内试验标定系数a和b,将现场测得的P 波波速、S1 波波速、S2波波速代入拟合函数,获得对应的y1,y2和y3后对其取平均值,从而预估岩石的应力范围。相较单一利用纵波波速的方法,采用纵波和横波波速综合预测岩石所处应力状态更有利于反映岩石的实际应力状态。
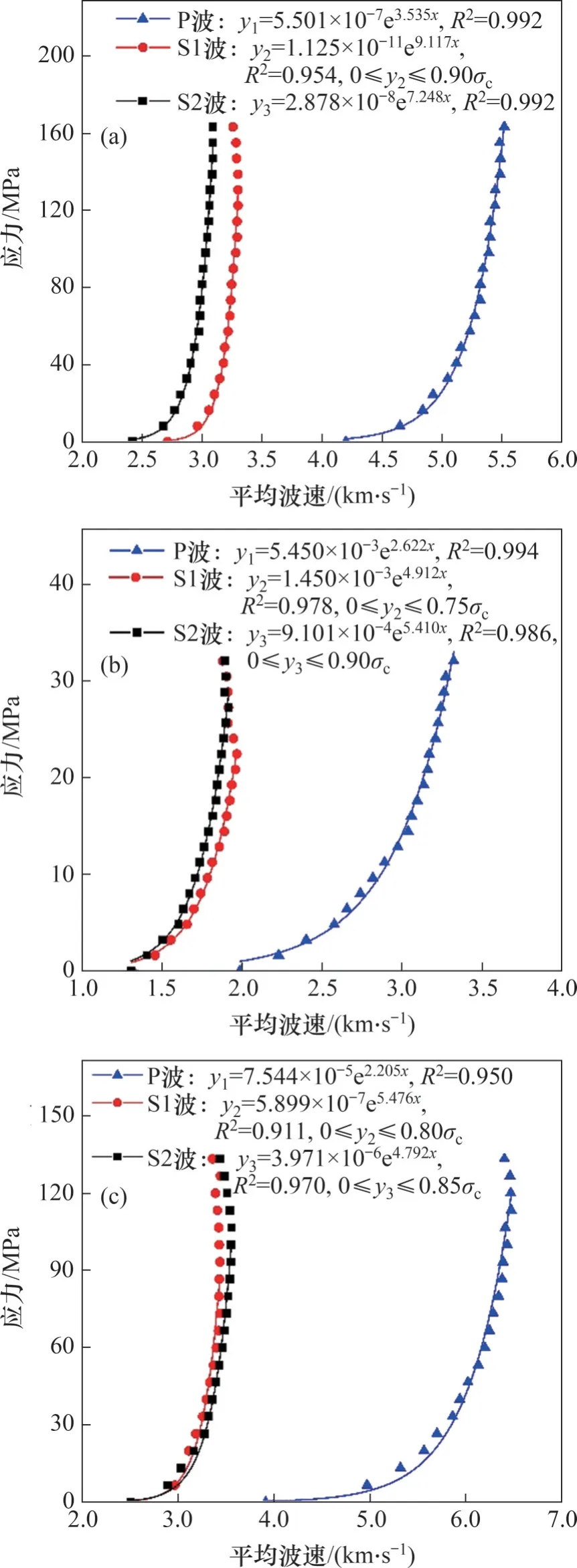
图5 岩石应力-波速拟合曲线Fig.5 Fitting curves of stress and wave velocity
3.3 岩石动弹参数变化规律
对于连续、均质、各向同性的岩石介质,根据波动理论,弹性波在介质中的传播满足下列公式[24]:
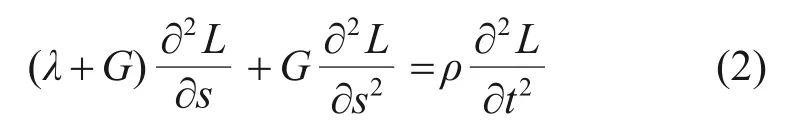
式中:λ和G为拉梅系数;L为质点在X或Z方向上的位移;t为时间;ρ为岩石密度。拉梅系数与泊松比和弹性模量存在如下换算关系:
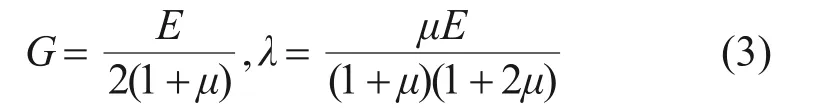
式中:μ为泊松比;E为弹性模量。
联立式(2)和(3)可获得纵、横波波速vp和vs:
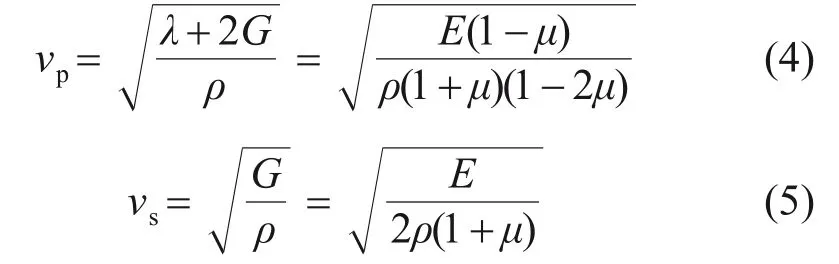
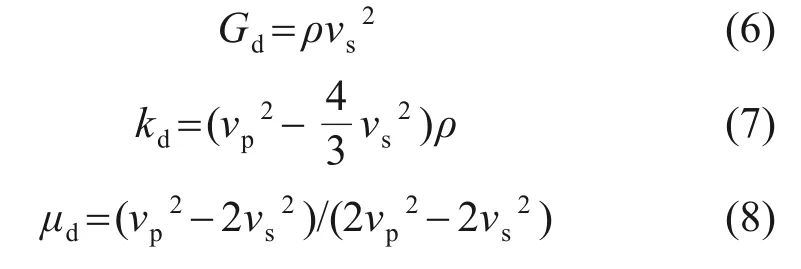
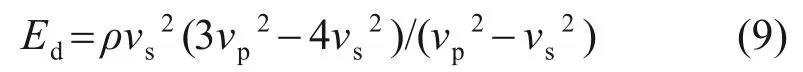
式中:Gd为岩石动剪切弹性模量;kd为岩石动体积弹性模量;μd为岩石动泊松比;Ed为岩石动弹性模量。
因此,已知岩石密度和加载过程中实时纵、横波速,可得到三类岩石平均动静弹参数变化规律,如图6所示,其中,Es为岩石静弹性模量,可利用应力-应变曲线计算得到。
弹性模量与泊松比是岩石的重要力学参数,弹性模量反映了材料抵抗形变的能力,泊松比是材料单向受压(拉)时,横向应变与轴向应变比值的绝对值,反映了材料的横向变形特性。由图6 可知,三类岩石动体积弹性模量与动泊松比在整个加载过程中一直呈增大趋势,其中红砂岩在进入下降阶段(Ⅲ)后泊松比增速显著增大,这是由于红砂岩孔隙率较大,进入裂隙扩展阶段扩容更加剧烈;三类岩石的动剪切弹性模量、动弹性模量在快速上升阶段(Ⅰ)与平稳增加阶段(Ⅱ)均持续增大,进入下降阶段(Ⅲ)后开始下降,表明此时膨胀作用大于结构黏聚力,岩石损伤严重;静弹性模量与动弹性模量在加载过程中有相同的变化趋势,动弹性模量大于静弹性模量,但两者数值关系需要进一步试验确定。
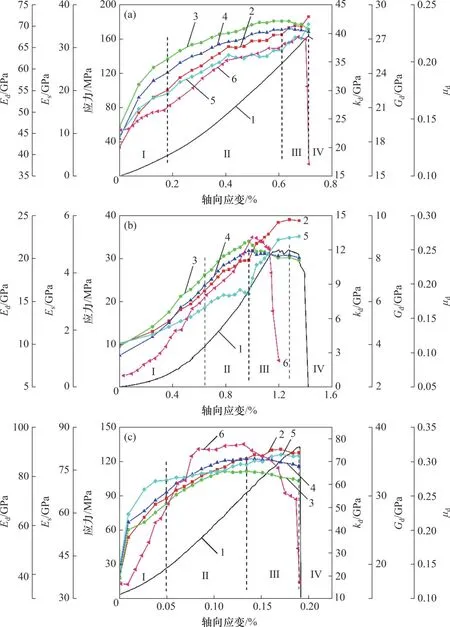
图6 压缩过程中动弹参数变化曲线Fig.6 Variation of dynamic elastic parameter during compression process
3.4 基于实时超声波参数的岩石损伤分析
利用超声波透过岩石后携带的声学参数(波速、波形、振幅、频率等)定量描述岩石的损伤情况,此处引入首波振幅定义的损伤变量:

式中:Ai为不同应力作用下纵波首波振幅;Amax为加载过程中纵波最大首波振幅;D为岩石的损伤因子,变化范围为0~1,D=0 表示无损伤状态,D=1表示破坏状态。
三类岩石在加载过程中首波振幅、损伤因子和动、静弹性模量的变化规律如图7所示。可以看出,在快速上升阶段(Ⅰ)和平稳增加阶段(Ⅱ),花岗岩和大理岩的损伤因子与动、静弹性模量快速增大;进入下降阶段(Ⅲ)时,花岗岩岩样的损伤因子达到0.96,大理岩岩样的损伤因子达到0.89,均接近于破坏,此时动、静弹性模量达到最大值并开始下降。
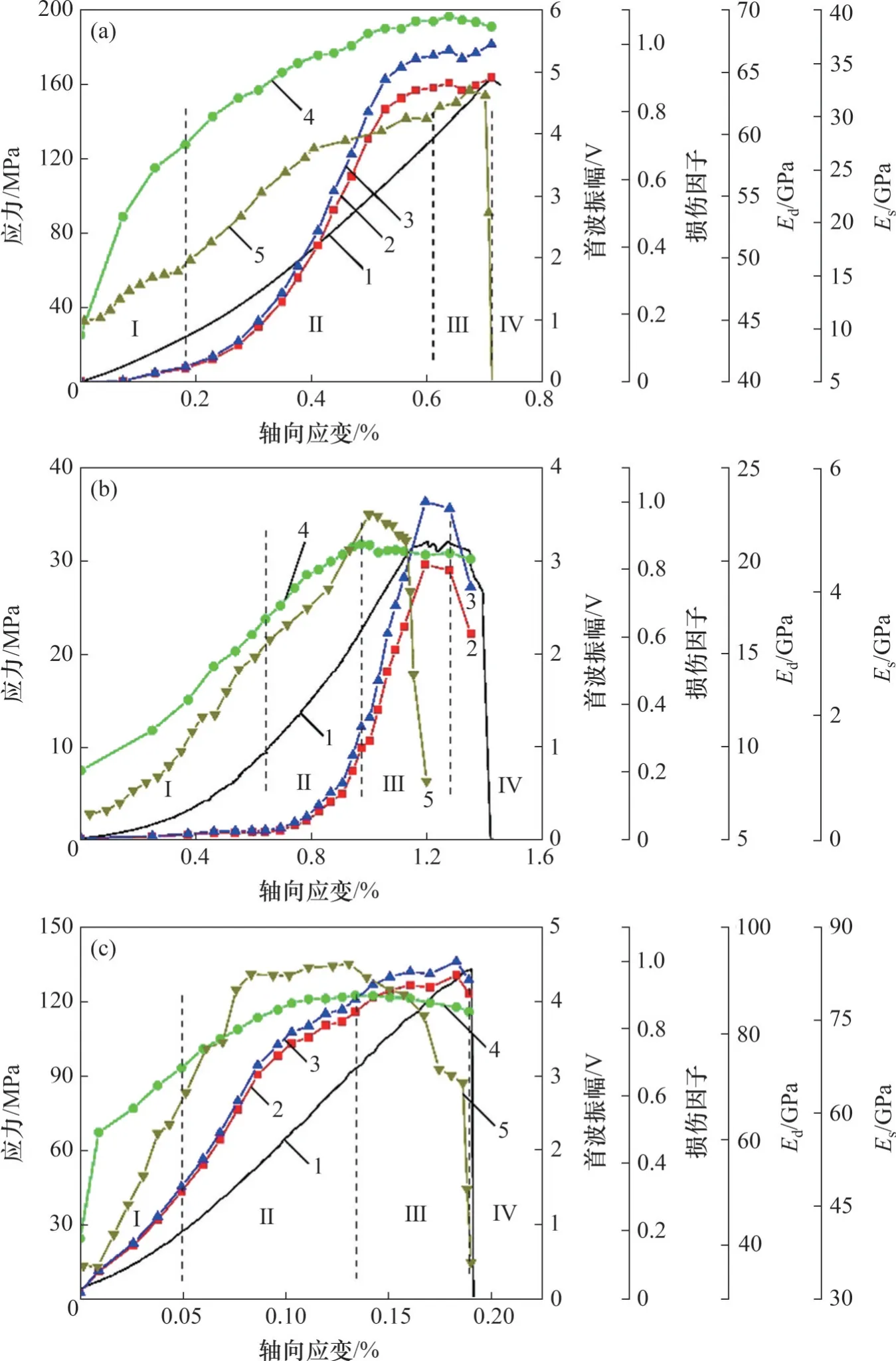
图7 岩石损伤因子变化曲线Fig.7 Variation of the rock damage factor
红砂岩在0.8%轴向应变之前,损伤因子增长很慢(接近于0),与花岗岩和大理岩明显不同,这是由于红砂岩孔隙率大,压密阶段长,首波振幅增长较慢;而在下降阶段(Ⅲ),红砂岩岩样的损伤因子开始快速增长并最终达到1,动、静弹性模量开始下降,岩样发生破坏。上述结果表明,利用首波振幅定义的损伤变量能够有效反映所研究岩石试样内部损伤发展的程度,有助于预测岩石破裂。
3.5 岩石破坏的实时超声波谱分析
利用Matlab 软件对波形图进行快速傅里叶变换,可得到岩石试件在单轴压缩过程中的实时纵、横波频谱图。为便于分析,提取其谱面积、主频和主频幅值,分别对其进行归一化处理,结果如图8~10所示。
谱面积与主频幅值可反映出声波信号通过岩石后的能量变化。由图8~10 可以看出:在加载过程中,随着岩石内部裂隙的压密、扩展、贯通,谱面积与主频幅值在不同阶段呈现出不同的变化特征。
由图8可知,花岗岩实时纵波谱面积与主频幅值在压缩过程中始终呈增大趋势,而横波谱面积与主频幅值在下降阶段(Ⅲ)出现明显下降,表明横波对花岗岩接近破裂时裂纹扩展的敏感性要比纵波的高。由图9 可知,红砂岩在加载过程中实时纵、横波谱面积与主频幅值呈现先上升后下降趋势,且横波谱面积与主频幅值下降时间节点比纵波的早,下降幅度比纵波的大,表明横波能更早、更明显地预测红砂岩的破坏。由图10 可知,大理岩实时纵、横波谱面积与主频幅值在下降阶段(Ⅲ)出现大幅下降,表明纵、横波均能很好地预测大理岩破坏。上述结果表明,针对所研究的岩石试样,实时纵、横波谱面积与主频幅值均能有效预测岩石破裂,其中实时横波的预测效果优于实时纵波的预测效果。

图8 花岗岩声学参数变化曲线Fig.8 Variation of granite acoustic parameters of samples
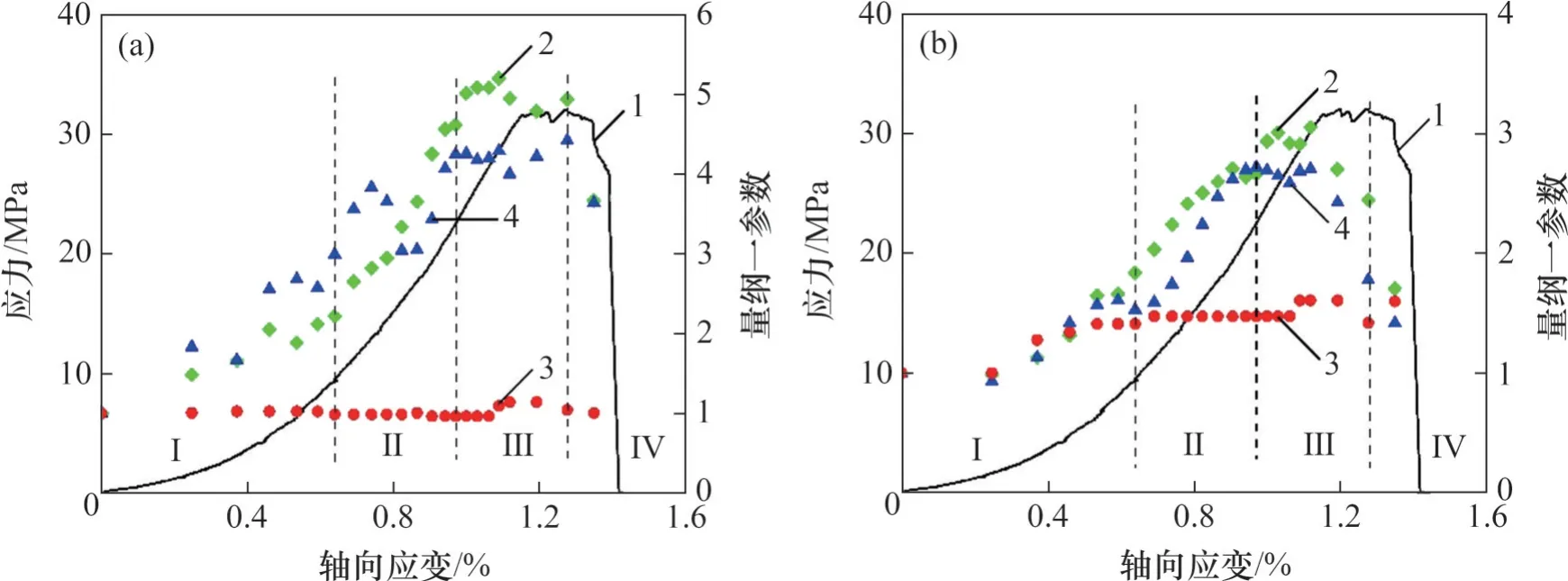
图9 红砂岩声学参数变化曲线Fig.9 Variation of acoustic parameters of red sand stone samples
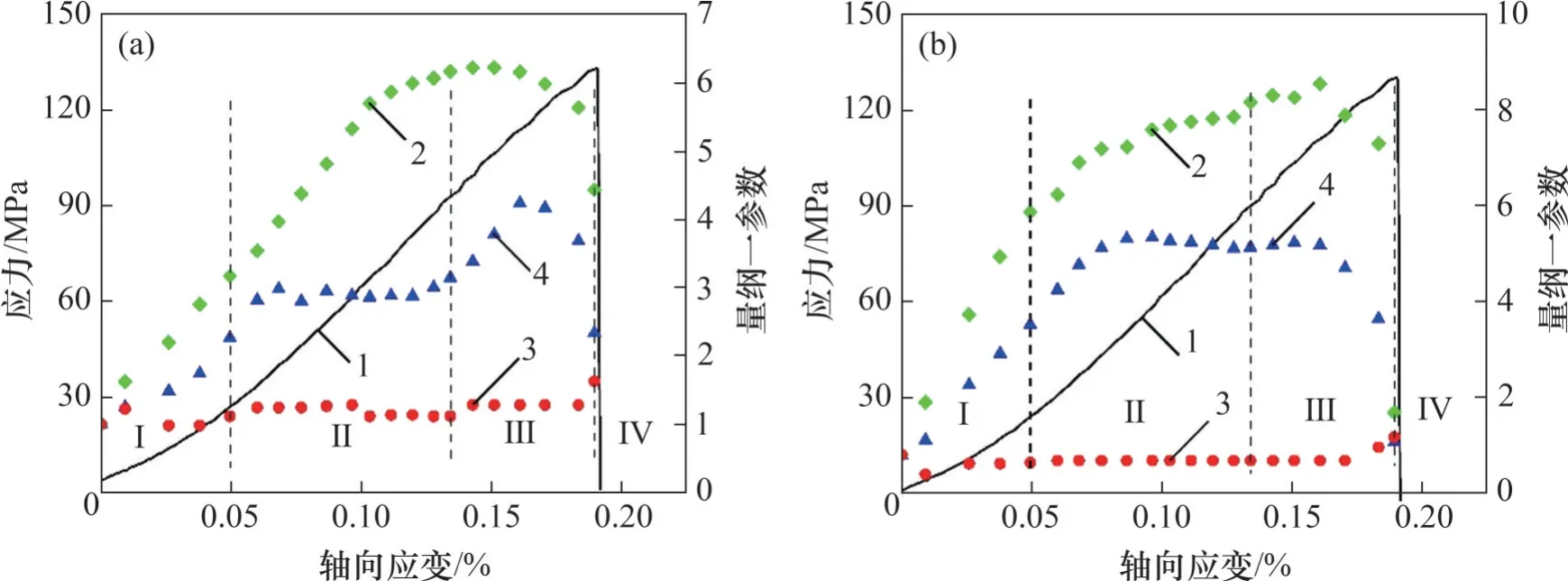
图10 大理岩声学参数变化曲线Fig.10 Variation of acoustic parameters of marble samples
此外,由图8~10 可以发现,通过傅里叶变换得到三类岩石的实时纵、横波主频只在加载初期与后期变化较大,与应力均没有明显的相关性。这主要是因为在低应力与高应力状态下,岩石内部裂缝压缩和扩展剧烈,导致接收到的超声波主频发生变化。
4 结论
1) 实时横波波速变化可分为快速上升阶段、平稳增加阶段和下降阶段,分别对应岩石裂纹的萌生、扩展和贯通;进入下降阶段后,实时横波波速先于实时纵波波速达到峰值点,表明实时横波波速峰值点可以作为所研究岩石,尤其是渐进性破坏特征明显的岩石试样破裂的前兆。
2) 试验所用花岗岩、红砂岩和大理岩这3类岩石压密方向的实时纵波波速和横波波速与岩石所处的应力状态呈指数函数关系。可通过室内试验标定系数a和b,然后将现场测得的P 波波速、S1和S2 波波速代入拟合函数并求取平均值来预估岩石的应力范围。
3) 试验所用花岗岩、红砂岩和大理岩这3类岩石动体积弹性模量与动泊松比在整个加载过程中一直呈增大趋势,动剪切弹性模量、动弹性模量、静弹性模量在快速上升阶段与平稳增加阶段均持续增大,进入下降阶段后开始下降,其中动弹性模量大于静弹性模量。
4) 对于花岗岩、红砂岩和大理岩这3类岩石试样,实时首波振幅定义的损伤变量能够有效反映岩石内部损伤发展的程度,实时纵、横波谱面积与主频幅值均能有效预测岩石破裂,其中实时横波的预测效果优于实时纵波的预测效果。
