有限粗渐近性质C-分解复杂度

李国强

（贵州财经大学 数统学院,贵阳 550025）

0 引言

文献[1]介绍了度量空间中的粗不变量: 有限渐近性质C-分解复杂度,以下简称有限APC-分解复杂度.有限分解复杂度[2]和渐近性质C (Asymptotic Property C,APC)[3]蕴含着有限APC-分解复杂度,而有限APC-分解复杂度又蕴含着性质A[4].本文的目的在于建立粗范畴意义下的有限APC-分解复杂度.

为了描绘度量空间的粗几何特征,文献[5]介绍了度量空间中的粗结构.文献[6]对群的粗结构进行了研究.结合文献[7]中对粗性质C和粗分解复杂度的介绍,在粗结构的意义下,可以引入有限APC-分解复杂度的概念,以便更好地理解这种性质.

1 准备知识

1.1 有限APC-分解复杂度

文献[1]结合有限分解复杂度[8-9]的分解思想和Dranishnikov 的渐近性质C[10]给出了有限APC-分解复杂度的概念.下面回顾文献[1]中有限APC-分解复杂度的定义及相关性质.本文延续文献[1]中所用的基本符号.

设(X,d)是一度量空间,r是一正实数,U是X的一个子度量空间族.如果对任意U,V∈U,U≠V,且对任意x∈U,y∈V,总有d(x,y)＞r,则称U是r-不相交的.

1.2 有限粗APC-分解复杂度

设X是一个集合,E和F是X×X的子集.定义E和F的复合(记为E◦F)为

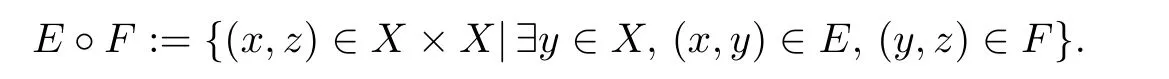
对任意n≥1,令

E的逆为

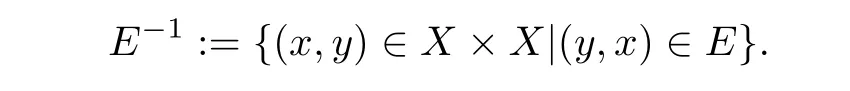
定义 3[5]设X是一个集合,E是X×X的一族子集,如果E满足下面5 个条件:

(1) 如果E∈E,F⊆E,则F∈E;

(2) 如果Ei∈E,i=1,2,···,n,则

(3) 对角线△X:={(x,x)∈X ×X|x∈X}∈E;

(4) 如果E∈E,则E-1∈E;

(5) 如果E,F∈E,则E◦F∈E.

则称E为X上的粗结构,E中的元素称为控制集,(X,E) 称为粗空间.

如果控制集E满足E=E-1,则称E是对称的.现在考虑粗空间若子集B满足B×B∈E,则称B有界.设U是X的一个子集族,如果,则称U是一致有界的.对于一个控制集E,如果对任意A,B∈U,A≠B,有 (A×B)∩E=∅,则称U为E-不相交的.对任意x∈X,定义E[x]:={y∈X|(y,x)∈E}.当n=0 时,规定En=△.

下面的定义可参考文献[5].设 (X,E)和(Y,F)是两个粗空间,f:X→Y是一个映射.如果对X中的任意控制集E∈E,有

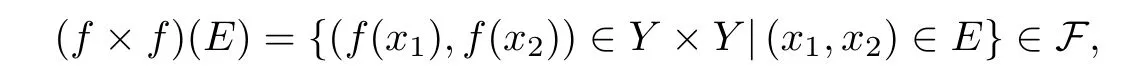
则称f是扩张的.如果对任意有界集B⊆Y,f-1(B) 在X中有界,则称f是恰当的.如果f既是扩张的又是恰当的,则称f是粗映射.如果f是粗映射,且对任意F∈F,有

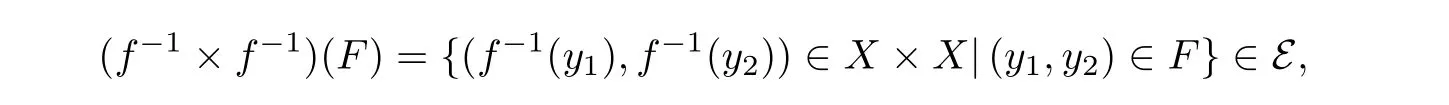
则称f为粗一致嵌入.设映射f,f′:X→Y,如果{(f(x),f′(x))∈Y×Y|x∈X}∈F,则称f和f′是相近 的.对于空间X和Y,如果存在两粗映射f:X→Y和g:Y→X,使得f◦g和g◦f分别与Y和X上的恒等映射相近,则称X和Y是粗等价的.

下面把有限APC-分解复杂度的概念由度量空间的范畴移植到Roe 的粗空间范畴上.

定义 4设X和Y是粗空 间 (Z,E) 的两个 粗子空间族,L={L1,L2,···}∈EN.如果存 在整数k,使得对每个X∈X,存在Y的一列子集族U1,U2,···,Uk,满足每个Ui是Li-不相交的,且,则称X在Y上是一致L-分解的.把“X在Y上是一致L-分解的”简记为

定义 5设是粗空间 (X,E) 的所有一致有界子集族的全体.对每个序数α＞0,令

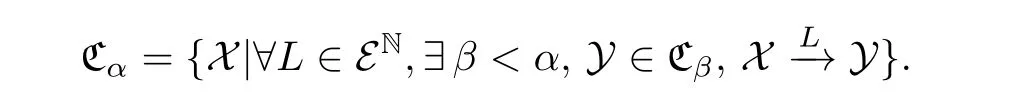
关于有限粗APC-分解复杂度,有下面的事实.

引理 2设X是粗空 间 (Z,E) 的一族 粗子空 间,α和β是两个序数.如 果α＞β,X∈,则X∈

特别地,度量空 间 (X,d)是粗空 间,X×X的子集E是控制 集当且 仅当存 在r＞0,使得E={(x,y)∈X ×X|d(x,y)≤r}.度量空间 (X,d) 作为粗空间,它的粗结构称为有界粗结构.下面将说明度量空间 (X,d) 具有有限APC-分解复杂度当且仅当X作为粗空间具有有限粗APC-分解复杂度.这样,在某种意义上用“正确”的方式定义了有限粗APC-分解复杂度.

性质 1设 (X,d)是一个度量空间,E是作为粗空间X的粗结构.则 (X,d) 具有有限APC-分解复杂度当且仅当(X,E) 具有有限粗APC-分解复杂度.

证明先假设 (X,E) 具有有限粗APC-分解复杂度,且{X}∈α.对任意R={R1,R2,···}∈RN,考虑一列控制集L={L1,L2,···},其中Li={(x,y)∈X ×X|d(x,y)≤Ri}.由于{X}∈α,故存在β＜α和Y∈使得,即存在整数k和Y的一列子集族U1,U2,···,Uk,使得每个Ui是Li-不相交的,且由于Ui是Li-不相交的,所以对任意A,B∈Ui,A≠B,有(A×B)∩Li=∅.那 么,如果a∈A,b∈B,则 有 (a,b)∈/Li.因此,d(a,b)＞Ri,这表 明Ui是Ri-不 相交的.所 以,(X,E)具有有限粗APC-分解复杂度,故 (X,d) 具有有限APC-分解复杂度.

反之,假设 (X,d) 具有有限APC-分解复杂度,且{X}∈α.L={L1,L2,···}∈EN是一列控制集,定义R={R1,R2,···}∈RN,其中

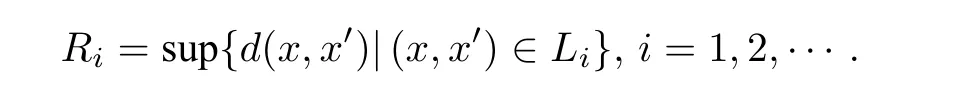
由有界粗结构的定义知,每个Ri都是有限的.由于{X}∈α,则存在β＜α和Y∈β,使得,即存在整数k和Y的一列子集族U1,U2,···,Uk,满足每个Ui是Ri-不相交的,且X=i Ui.为 了完成证明,需 要证明Ui是Li- 不相交 的.假设A,B∈Ui,A≠B,a∈A,b∈B,且 (a,b)∈Li,则有d(a,b)≤Ri,这和Ui是Ri-不相交 的事实 相矛盾.所 以,当A,B∈Ui,A≠B时,有(A×B)∩Li=∅ .因此,如果 (X,d) 具有有限APC-分解复杂度,则 (X,E) 具有有限粗APC-分解复杂度.

2 有限粗APC-分解复杂度的保持性质

本章证明有限粗APC-分解复杂度是粗几何不变量且关于取子集是保持的,再给出有限粗APC-分解复杂度的纤维引理.由此,有限粗APC-分解复杂度在直积运算下是封闭的.

下面证明有限粗APC-分解复杂度在子集下的遗传性.

性质 2设 (X,E)是粗空间.如果Y⊆X,Y继承X上的粗结构,且X具有有限粗APC-分解复杂度,则Y也具有有限粗APC-分解复杂度.

证明假设{X}∈α,证明{Y}∈α.设L={L1,L2,···}∈EN,则存在β＜α和Y∈β,使得,即存在整数k和Y的一列子集族U1,U2,···,Uk,满足每个Ui是Li-不相交的,且定义

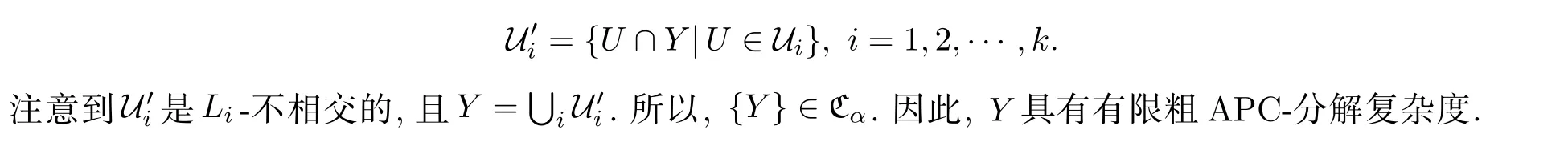
定理 1有限粗APC-分解复杂度是粗不变量.

证明设 (X,E)和(Y,F)是两个粗等价 的粗空间.下面证明 如果映射f:X→Y是粗 一致嵌入,且{Y}∈α,则{X}∈α.

首先假设{Y}∈0,即Y有界,Y×Y∈F.因为,f是粗一致嵌入,所以,得

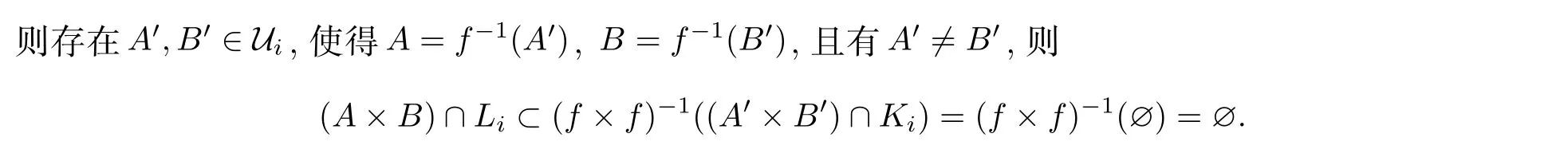
因为Ui是Ki-不相交的,这样就得到Vi是Li-不相交的,注意到α+γ＜α+β,所以f-1(Y)∈α+β.

性质 3设 (X,E)和(Y,F)是两个粗空间,f:X→Y是扩张映射.假设存在α,使得对Y的任意一个一致有界子集族V,有f-1(V)∈α,则如果存在β使得{Y}∈β,那么{X}∈α+β.

证明由引理3 可知此结论成立.

为了证明有限粗APC-分解复杂度在积运算下是封闭的,可利用Grave 在文献[11]中定义的标准有界粗结构.如果 (Xi,Ei)是一列有限粗空间族,i=1,2,···,k,其乘积空间X1×X2×···×Xk的粗结构如下:

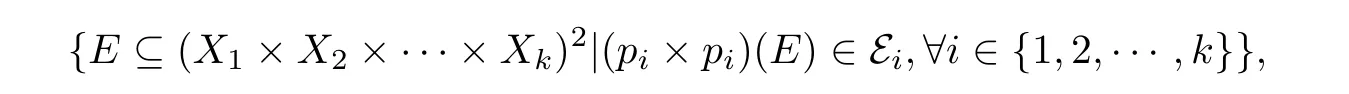
其中,pi记作X1×X2×···×Xk的第i个因子的投影.

引理 4设 (X,E)和(Y,F)是两个粗空间,B是X中的有界子集,且B继承X中的粗结构,B×Y是乘积粗空间,则B×Y与Y粗等价.

证明考虑b0∈B,定义映射g:Y→B×Y为g(y)=(b0,y) .显然,g是粗一致嵌入.定义f:B×Y→Y为f(b,y)=y.下面说明f也是粗一致嵌入.由上述粗空间乘积的定义知,f是扩张的.另外,f是恰当的.事实上,如果C⊆Y是有界的,则有f-1(C)=B×C在乘积粗结构中也是有界的.令K∈F,因为,B×B∈E,所以,有 (p1×p1)(f-1(K))=B×B∈E和(p2×p2)(f-1(K))=K∈F.这样就得到f-1(K)是粗空间X×Y中的控制集.因此,f是粗一致嵌入.

再证明f◦g和g◦f分别与Y和B×Y的恒等映射相近.显然,f◦g:Y→Y本身就是恒等映射.g ◦f:B×Y→B×Y与恒等映射相近,这是因为

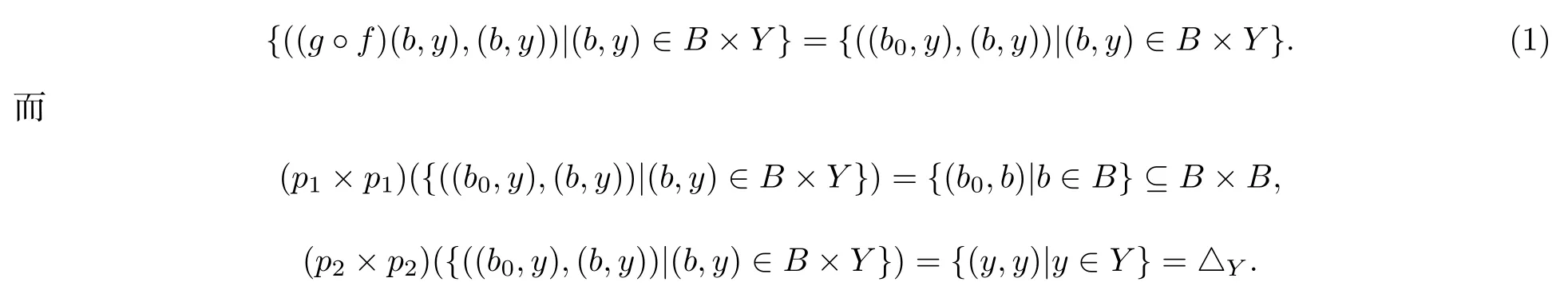
则 (p1×p1)({((b0,y),(b,y))|(b,y)∈B×Y})和(p2×p2)({((b0,y),(b,y))|(b,y)∈B×Y}) 均为控制集,所以,式(1)中的集合为乘积粗空间B×Y中的控制集.

性质 4设 (X,E)和(Y,F)是两个粗空间,Z=X ×Y是乘积粗空间.如果X,Y具有有限粗APC-分解复杂度,则Z也具有有限粗APC-分解复杂度.

证明假设{X}∈α,{Y}∈β.令f:Z→X为投影映射.注意到f是扩张映射.假设V是X中一族一致有界的子集族,由定义知{V ×V|V∈V}∈E.如果A∈f-1(V),则存在V∈V,使得A=V ×Y.由引理4 知,每个A∈f-1(V) 与Y都是粗等价的.这样由性质3 知{Z}∈α+β.因此,Z具有有限粗APC-分解复杂度.

3 有限粗APC-分解复杂度与粗性质A

本章借助文献[1]中的思想,在粗结构的意义下证明具有有限粗APC-分解复杂度的粗空间具有粗性质A,用文献[7]中的技巧定义粗空间上的度量.

引理 5设 (X,E)是粗空 间,E是E中的一 个对称 控制集.定义映 射D:X ×X→Z∪{+∞}为D(x,y)=min{k≥0|(x,y)∈Ek},则D是一个度量.

在度量空间的意义下,性质A 有许多种等价定义[12].在文献[7]中,作者利用l1(X) 的映射的存在性给出了性质A 在粗空间下的定义.设 (X,E)是粗空间，ξ是X到Banach 空间的映射，记X中的元素x在ξ下的象为ξx.

定义 6设 (X,E)是粗空间,若对任意ε＞0和任意F∈E,存在映射ξ:X→l1(X),使得

(1)对任意x∈X,有‖ξx‖=1 ;

(2)对任意 (x,y)∈F,有

(3)存在S∈E使得对每个x∈X,s uppξx ⊆S[x] .则称 (X,E) 具有粗性质A.

定义 7设ξ:X→l1(X)是一映 射,若对任 意k∈N,(x1,x2)∈X且D(x1,x2)≤k,总有,则称ξ具有ϵ-变差.

定义 8若映射ξ:X→l1(X) 满足: 对任意x∈X,有‖ξx‖=1,则称ξ是标准的.

定义 9设 (X,E)是粗空间,ξ:X→l1(X)是一映射,E是E中的一个对称控制集.若存在n∈N,使得对每个x∈X,有 s uppξx En[x],则称ξ是n-粗局部支撑.

下面,利用上述的定义给出粗性质A 的另外一种叙述方式.

定义 10设 (X,E)是粗空 间,E是E中的一 个对称 控制集.若对任 意ϵ＞0,存在映射ξ:X→l1(X)使得:

(1)ξ是标准的;

(2)ξ具有ϵ-变差;

(3) 存在n∈N,使得ξ是n-粗局部支撑.则称X具有粗性质A.

引理6设(X,E)是粗空间,固定E中的一个对称控制集E.若ξi:X→l1(X)(i∈I,I为指标集)具有ϵi-变差,则具有变差.

引理 7设 (X,E)是粗空间,固定E中的一个对称控制集E,ϵ＞0 .映射ξ:X→l1(X) 具有ϵ-变差,且对任意的x∈X,有‖ξx‖≥1 .若记映射是标准的且具有 2ϵ-变差.

引理 8设 (X,E)是粗空间,固定E中的一个对称控制集E,U⊆X.若ξ:U→l1(U)是标准的且具有ϵ-变差的m-粗局部支撑映射,对任意的n∈N,定义N(U,n)={x∈X|D(x,U)≤n},则存在粗局部支撑映射:X→l1(X),满足:

(1) 对任意x∈X,D(x,U)＞n,有

(2) 对任意x∈U,有

证明定义映射α:X→[0,1]为

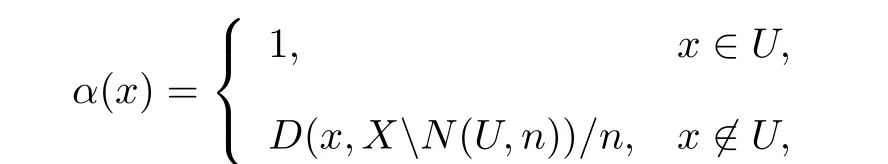
则α是李普希茨映射.事实上,若x,y∈U或者x,y∈XN(U,n),则

若x,y∈N(U,n)U,则

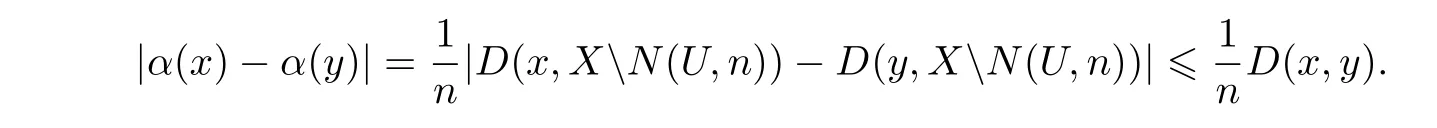
若x∈XN(U,n),y∈N(U,n)U,则

则可以得到一个标准的且具有ϵ-变差的 (m′+n′)-粗局部支撑映射ξ:X→l1(X) .

定理 3设 (X,E)是粗空间,若X具有有限粗APC-分解复杂度,则X具有粗性质A.

证明假设则对任意L∈EN,存在β＜α和Y,使得.注意到任何一致有界族都具有一致粗性质A,由归纳法假设可知,Y具有粗性质A.由定理 2 可知,{X}具有一致粗性质A,则X具有粗性质A.

4 粗性质C和粗分解复杂度

定义 11[7]设 (X,E)是粗空间.若对任何一列控制集E1⊆E2⊆E3⊆···,存在整数n和X的有限子集族序列U1,U2,···,Un,使得

(2) 每个Ui是一致有界的;

(3) 每个Ui是Ei-不相交的.则称 (X,E) 具有粗性质C.

定理 4设 (X,E)是粗空间,则X具有粗性质C 当且仅当{X}∈.

证明若X具有粗性质C.对任意L∈EN,存在整数n和X的有限子集族序列U1,U2,···,Un,该序列满足定义4 中的条件.令Y={U|U∈Ui,i=1,2,···,n},则Y是一致有界的,即Y∈.注意到,则有

反过来,如果{X}∈C1,对任意一列控制集L1⊆L2⊆L3⊆···,令L={L1,L2,L3,···},则存在使得,显然,X满足粗性质C 的条件.

设 (X,E)是粗空间.Y是X的一族粗子空间,L∈E是一控制集.称X在Y上是L-分解的,如果存在分解

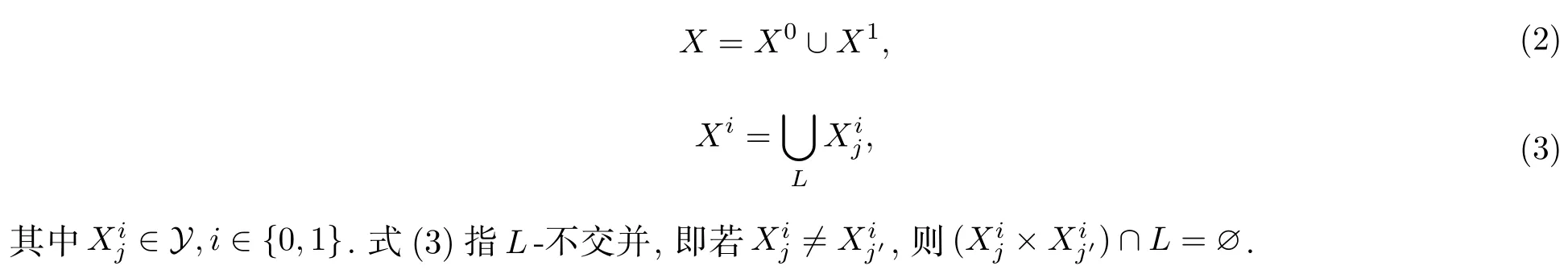
设X和Y是粗空间 (Z,E) 的两族粗子空间,L是一控制集.如果每个X∈X在Y上是L-分解的,则称X在Y上是L-分解的.

一族粗空间Y是一致有界的,如果是控制集.另外,可以把一个粗空间X的分解理解为一粗空间族{X}的分解.对于粗空间X,做下面一个粗分解游戏: ①玩家1 给出一个控制集L1,玩家2 给出一族粗空间Y1,使得{X}在Y1上是L1-分解的;② 玩家1 给出一个控制集L2,玩家2 给出一族粗空间Y2,使得Y1在Y2上是L2-分解的.这个游戏按这种方式一直玩下去,直到玩家2 胜出为止.玩家2 胜出是指存在k∈N,使得玩家2 能够在一族一致有界的粗空间上分解Yk-1.

定义 12[7]设 (X,E)是粗空间.如果玩家2 能在对{X}的粗分解游戏当中胜 出,则称X具有有 限粗分解复杂度.

定义 13[7]设 (X,E)是粗空间.如果对任意一列控制集L1⊆L2⊆···,存在X的有限粗子空间族Y1,Y2,···,Yk,使得,且Yk一致有界,则称X具有直有限粗分解复杂度.

设 (X,E)是粗空间,Y是X的一族粗子空间.L∈E是一个控制集,d是一个正整数.如果

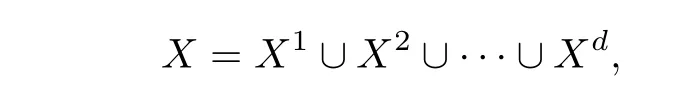
使得对每个i=1,2,···,d,有,

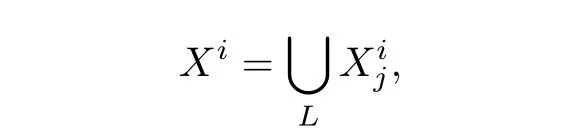
定义 14[7]设 (X,E)是粗空间.如果玩家2 能在对{X}的弱粗分解游戏中胜 出,则称X具有有 限弱粗分解复杂度.

定理 5设 (X,d)是一度量空间,E是X上的有界粗结构,则以下结论成立:

(1) (X,d) 具有有限弱分解复杂度当且仅当(X,E) 具有有限弱粗分解复杂度;

(2) (X,d) 具有有限分解复杂度当且仅当(X,E) 具有有限粗分解复杂度;

(3) (X,d) 具有直有限分解复杂度当且仅当(X,E) 具有直有限粗分解复杂度.

证明(1) 首先,假设 (X,d) 具有有限弱分解复杂度.当玩家1 任给出一控制集L1和正整数d1时,定义

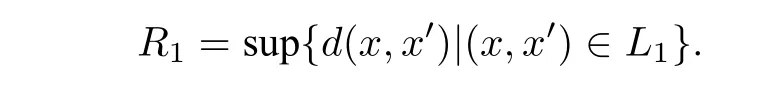
由 于 (X,d) 具有有 限弱分 解复杂 度,故存在X1,使得X在X1上是 (R1,d1)-分解的,即有其中Uj ⊆X1且Uj是R1-不相交的.

下面需要证明Uj是L1-不相交的,即对任意A,B∈Uj,A≠B,有 (A×B)∩L1=∅ .假设a∈A,b∈B,(a,b)∈L1,则有d(a,b)≤R1,这与Uj是R1-不相交矛盾.所以,X在X1上是 (L1,d1)-分解的.

当玩家1 给出控制集Li和正整数di时,定义

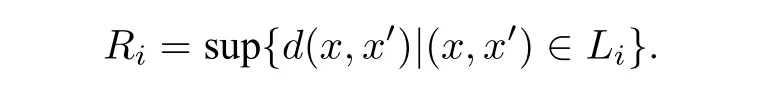
则存在Xi,使得Xi-1在Xi上是 (Ri,di)-分解的.类似地,可以得到Xi-1在Xi上是 (Li,di)-分解的.由于(X,d) 具有有限弱分解复杂度,经过有限步之后,分解游戏结束.不妨设在第k步,存在一致有界子空间族Xk,使得Xk-1在Xk上是(Rk,dk)-分解的.同样地,Xk-1在Xk上是(Lk,dk)-分解的.

现在需要证明Xk是粗一致有界的.事实上,具有一致有界的直径,即有,则

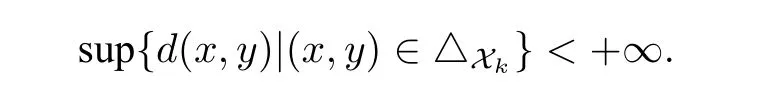
即△Xk∈E.所以,(X,d) 具有有限弱分解复杂度,则 (X,E) 具有有限弱粗分解复杂度.

反过来,假设 (X,E) 具有有限弱粗分解复杂度.当玩家1 任给R1＞0和正整数d1时,定义一控制集L1:

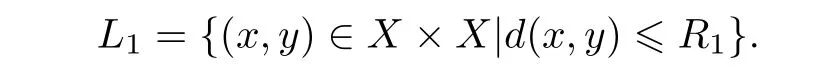
由 于(X,E)具有有限粗弱分解复杂度,故存在X1,使得X在X1上是 (L1,d1)-分解的,即有X=其中Uj⊆X1且Uj是L1-不相交的.

下面需 要证明Uj是R1-不 相交,即对 任意A,B∈Uj,A≠B,有d(A,B)≥R1.事 实上,对任意A,B∈Uj,A≠B,有 (A×B)∩L1=∅ .所以,若a∈A,b∈B,则 (a,b)∈/L1,即有d(a,b)＞R1.这样,得到Uj是R1-不相交的.

当玩家1 给出Ri＞0和正整数di时,定义

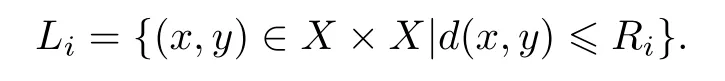
则存在Xi使得Xi-1在Xi上是 (Li,di)-分解 的,类似地,可以得到Xi-1在Xi上是 (Ri,di)-分解的.由于(X,E) 具有有限粗弱分解复杂度,经过有限步之后,粗分解游戏结束.不妨设在第k步,存在粗一致有界子空间族Xk,使得Xk-1在Xk上是 (Lk,dk)-分解的.同样地,Xk-1在Xk上是 (Rk,dk)-分解的.由于Xk是粗一致有界的,故.则有

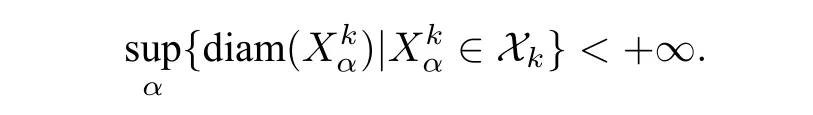
因此,Xk是度量一致有界的.这样就证明了 (X,E) 具有有限弱粗分解复杂度,则 (X,d) 具有有限弱分解复杂度.

(2) 在(1)中取每个di=2 就得到了(2)的证明.

(3)首先,假 设 (X,d) 具有直 有限分 解复杂 度.L={L1,L2,L3,···}是一列 控制集,其中L1⊆L2⊆L3⊆···.对每个i,定义

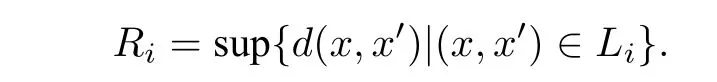
由有界粗结构的定义知,每个Ri是有限的,且有R1≤R2≤R3≤···.另一方面,令R1≤R2≤R3≤···是一列正数,定义

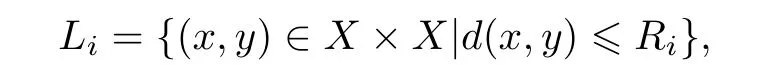
得到L1⊆L2⊆L3⊆···,L={L1,L2,L3,···}是一列控制集.剩下的证明与(1)的证明思想是一样的,这里不再赘述.证毕.