工业机器人能耗预测研究
2022-11-25庹军波彭秋媛张贤明李聪波
庹军波 彭秋媛 张贤明 李聪波
1.重庆工商大学废油资源化技术与装备教育部工程研究中心,重庆,400067 2.重庆工商大学机械工程学院,重庆,400067 3.重庆大学机械传动国家重点实验室,重庆,400044
0 引言
由于降低能源消耗是实现“双碳”目标最直接有效的方法之一,故节能研究已成为我国碳达峰碳中和事业的重要组成部分[1]。全球工业机器人累计安装已达270余万台套,其中,中国已达到78.3余万台,总量居亚洲第一,且呈递增趋势[2]。假设一台工业机器人功率为10 kW,一天工作8小时,则我国工业机器人年耗电量将达229亿千瓦时,全球年耗电量将达788亿千瓦时。由此可见,工业机器人耗电量巨大,其节能研究意义重大。
目前,国内外学者对机器人节能优化展开了研究。ZHANG等[3]从历史数据角度出发,提出了基于数据驱动的工业机器人能耗优化方法;PARYANTO等[4]根据能耗仿真模型提出了基于运动参数的工业机器人节能策略;许艳英等[5]采用蚁群算法进行了机器人模糊控制器的节能优化;郭锐等[6]从全局功率匹配角度出发,建立了一种机械臂轨迹优化的节能方法。
能耗预测或获取是能耗优化的数据基础,部分学者也对工业机器人能耗预测展开了研究。颜克[7]从物理能耗模型、数字描述模型、数字虚拟模型等多角度出发,进行了工业机器人能耗仿真预测研究;吴勇强等[8]根据永磁同步电机、伺服驱动器等主要功耗部件的能耗特性,建立了工业机器人功率等效模型,实现了工业机器人电机参数未知条件下的功率预测;PARYANTO等[9]通过分析控制系统、永磁同步电机和机械结构的关系,建立了集三者于一体的工业机器人仿真预测模型。此外,丁云鹏[10]提出了一种基于改进BP神经网络算法的关节最小能耗软测量模型,能够实现未知角位移和未知负载情况下的能耗计算;张浩杰等[11]构建了机器人动力学模型及其在运动过程中的动态能耗模型,实现了不同路径的能耗预测;贺莹[12]则结合焦耳定律,建立了多关节电机热损耗模型和电机能耗预测模型。以上预测或计算模型主要是基于机器人动力学模型开展的,预测时往往需要测量角速度、关节力矩、摩擦力矩等参数。由于测量参数众多、操作过程繁琐,且部分工业机器人测量仪器安装困难,故以上方法虽预测精度较高,但工业应用和推广十分受阻。
为避免上述缺陷,本文提出了一种简单易推广的能耗预测方法,具有操作方便、测量参数少,预测精度满足大多工业需求等特点,可为工业机器人的现有节能措施提供模型和数据支撑,例如,可为支持节能优化的动态建模[13]提供函数模型参考,可为最小能耗控制系统仿真[10]提供验证途径,可为低能耗最优路径规划方法[11]提供能耗数据,具有较广阔的应用前景。
1 工业机器人元动作
元动作的概念为“动作的动作”,一是指“动作的元件”或“动作的原型”,二是指“最初的动作”或“动作的构件”[14],其边界由“动作”概念而定。将工业机器人执行单位任务看成一个“动作”,则工业机器人元动作可分为动态元动作和静态元动作。动态元动作是指执行末端易区分和观察的动作,见表1,各动态元动作又分为空载元动作和负载元动作;静态元动作则是工业机器人静态运行(如待机或者预热)时的动作,通常不同位姿或负载的静态运行视为不同的静态元动作。
2 元动作能耗描述函数
2.1 静态元动作的能耗描述函数
工业机器人静态运行时的功率与机器人末端的空间位置(或位姿)、机器人末端负荷、运行组件的构成相关,故静态元动作的能耗描述函数表征如下:
Ps=f(x,y,z,m,c1,c2,…)
(1)
式中,Ps为静态元动作功率;x、y、z为执行末端的空间位置坐标;m为负荷质量;c1、c2为静态运行相关组件的运行状态,通常其值为1表示开启,为0表示停运状态。
鉴于大部分工业机器人静态运行状态仅为待机状态,且不同位姿时的待机功率相差很小,故当精度要求不同时,静态元动作的能耗描述函数可简化为
Ps=f(m)
(2)
2.2 移动元动作的能耗描述函数
工业机器人移动元动作通常分为X轴移动元动作、Y轴移动元动作、Z轴移动元动作。鉴于移动过程的功率与执行末端的空间位置、移动速度、执行末端负荷相关,故移动元动作的能耗描述函数可用下式表征:
Pm=f(x,y,z,m,v)
(3)
式中,Pm为移动元动作功率;v为执行末端的移动速度。
2.3 转动元动作的能耗描述函数
工业机器人转动元动作通常分为X轴转动元动作、Y轴转动元动作、Z轴转动元动作。由于转动过程的功率与执行末端的空间位置、旋转角速度、执行末端负荷相关,故转动元动作的能耗描述函数可用下式表征:
Pr=f(x,y,z,m,ω)
(4)
式中,Pr为转动元动作功率;ω为角速度。
2.4 执行末端元动作的能耗描述函数
执行末端元动作因工业机器人的用途不同而有所差异,如搬运机器人为抓取动作、焊机机器人为焊接动作,它们的能耗描述函数需根据各自运动特点单独创建。
3 基于元动作的能耗预测
基于元动作的工业机器人能耗预测流程如图1所示。首先,建立机器人的元动作库,离线测量各元动作功率并建立描述元动作能耗的数据库或函数库;然后,基于所建元动作库对目标过程进行元动作分解;最后,采用元动作能耗计算模型计算各元动作能耗以及目标过程总能耗。其中,各元动作能耗计算模型及总能耗计算模型如下。
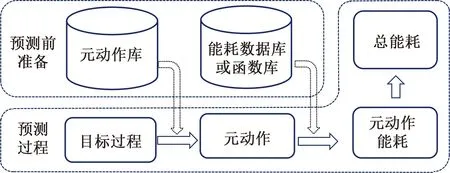
图1 能耗预测过程示意图
3.1 静态元动作能耗计算模型
静态元动作总能耗为各静态元动作能耗之和,而各静态元动作能耗为该元动作功率与运行时间的乘积,即
(5)
式中,Psi为第i个静态元动作的功率;Tsi为第i个静态元动作的运行时间;I为静态元动作总数量。
3.2 移动和转动元动作能耗计算模型
移动元动作空载和负载时的元动作能耗计算模型分别如下:

(6)
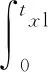
(7)
式中,Emu、Eml分别为空载和负载过程总能耗;Pxu(t)、Pyu(t)、Pzu(t)分别为X轴移动元动作、Y轴移动元动作和Z轴移动元动作空载时的功率;txu、tyu、tzu为相应的空载运行时间;Pxl(t)、Pyl(t)、Pzl(t)分别为X轴移动元动作、Y轴移动元动作和Z轴移动元动作负载时的功率;txl、tyl、tzl为相应的负载运行时间。
实施时,式(6)和式(7)中Pxu(t)、Pyu(t)、Pzu(t)、Pxl(t)、Pyl(t)、Pzl(t)的积分可在式(3)的基础上利用换元积分法进行积分,具体参见下节。
转动元动作空载和负载时的能耗计算模型分别如下:

(8)

(9)
式中,Eru、Erl分别为空载和负载过程总能耗;Pau(t)、Pbu(t)、Pcu(t)分被为X轴转动元动作、Y轴转动元动作和Z轴转动元动作空载时的功率;tau、tbu、tcu为相应的空载运行时间;Pal(t)、Pbl(t)、Pcl(t)分别为X轴转动元动作、Y轴转动元动作和Z轴转动元动作负载时的功率;tal、tbl、tcl为相应的负载运行时间。
同移动元动作的计算一样,具体实施时,亦可利用换元积分法进行积分。
3.3 执行末端元动作能耗计算模型
由于工业机器人执行末端元动作尚无统一的能耗描述函数,故当前执行末端元动作能耗计算往往直接采用现有相关的能耗预测模型(如文献[15]),或事先建立执行末端元动作能耗数据库,计算时直接调用。
3.4 总能耗计算模型
目标过程总能耗E为各组成元动作的能耗之和,即
E=Es+Emu+Eml+Eru+Erl+Ew
(10)
式中,Ew为执行末端元动作总能耗。
4 案例研究
4.1 概述
选用华数HSR-JR605工业机器人、LMG功率分析仪器开展了试验验证,试验现场如图2所示。

图2 试验现场
预测目标为将质量m=2.79 kg的物体从A处移至F处的过程,该过程中各方向移动速度均设为0.161 m/s,运动轨迹为C(376,0,332)→B(376,-248,332)→A(376,-248,112)→B(376,-248,332)→D(376,236,332)→E(495,236,332)→F(495,236,112)(单位:mm),如图3所示。计算时,该过程共分为9个阶段,具体见下述预测过程,各阶段运行参数和涉及的元动作类型见表2。

图3 运动过程示意图

表2 目标过程的运行参数
4.2 预测过程及结果
(1)第一阶段。第一阶段为点C到点B的空载移动过程,预测前通过试验测量和数据拟合得到Y轴移动元动作的能耗描述函数,如图4所示。令y=y0+vt(y0表示起点Y坐标,v表示移动速度,t表示运行时间),则有y=-0.161t,将其代入能耗描述函数,得
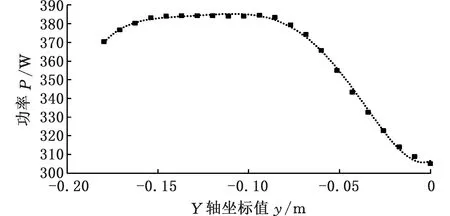
图4 元动作Y空载功率曲线
Pyu(t)=107(-0.161t)5+5×106(-0.161t)4+8.8×105(-0.161t)3+6.2×104(-0.161t)2+4.5×102(-0.161t)+306
将其代入式(6)得

(2)第二阶段。第二阶段为点B到点A的空载移动过程,该过程Z轴移动元动作的能耗描述函数如图5所示,换元后Pzu(t)为

图5 元动作Z空载功率曲线
Pzu(t)=4.5×104(0.332-0.161t)4-3.3×104(0.332-0.161t)3+8.5×103(0.332-0.161t)2-9.7×102(0.332-0.161t)+347
代入式(6)得

此阶段实际速度比设定速度快得多,实际运行时间仅0.6 s,相比理论的运行时间1.37 s要短得多,故造成该部分实测能耗也比预测能耗少得多。
(3)第三阶段和第四阶段。第三、四阶段为点A处的空载待机和负载待机,对应静态元动作功率分别为303 W和314 W,运行时间分别为21 s和69 s。此处静态元动作总能耗如下:
Es1=303×21+314×69=28 029 J
(4)第五阶段。第五阶段为点A到点B的负载移动过程,该过程Z轴移动元动作的能耗描述函数如图6所示,换元后Pzl(t)如下:
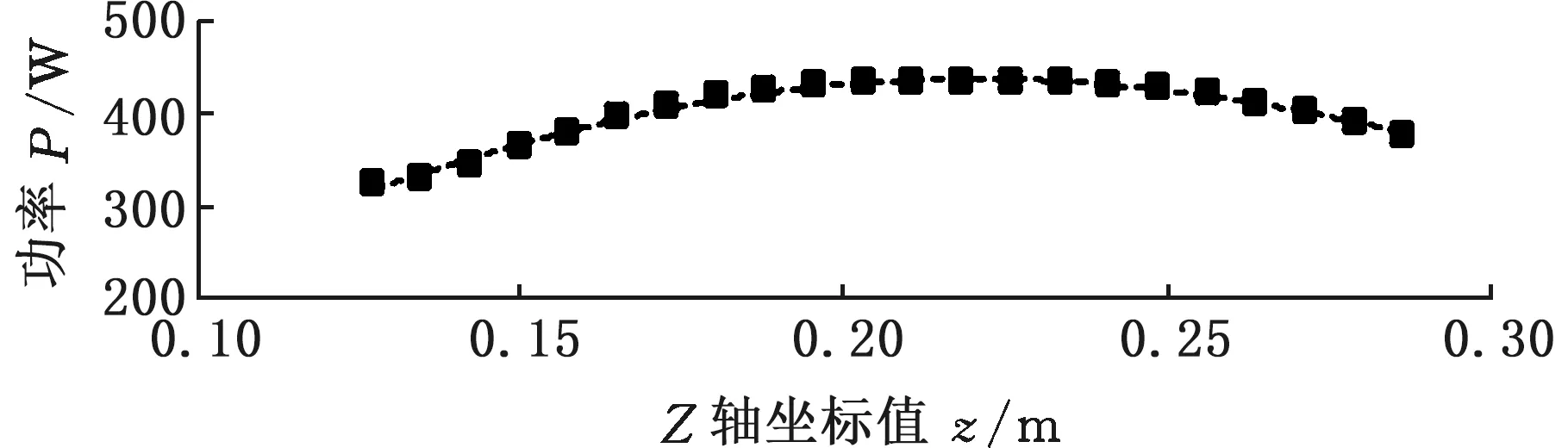
图6 元动作Z负载功率曲线
Pzl(t)=2.1×105(0.112+0.161t)4-1.7×105(0.112+0.161t)3+3.8×104(0.112+0.161t)2-7.6×102(0.112+0.161) + 93
代入式(7)得

(5)第六阶段。第六阶段为点B到点D的负载移动过程,为提高拟合精度,此过程Y轴移动元动作能耗描述函数采用分段拟合并分别计算能耗。
第一部分为点B到点C处,该过程Y轴移动元动作的能耗描述函数拟合结果如图7所示,换元后Pyl(t)的表达式如下:

图7 元动作Y负载功率曲线
Pyl(t)=-1.7×105(-0.248+0.161t)4-8.0×104(-0.248+0.161t)3-1.3×104(-0.248+0.161t)2-8.2×102(-0.248+0.161t)+344
代入式(7)得

第二部分为点C到点D,其能耗描述函数拟合结果如图8所示,换元后得Pyl(t)如下:

图8 元动作Y负载功率曲线
Pyl(t)=-9×10-5×(0.161t)5+1×10-2×(0.161t)4-0.5×(0.161t)3+7.5×(0.161t)2-38.3×(0.161t)+ 372
代入式(7)可得能耗为
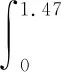
故第六阶段的总能耗为
Eyl=Eyl1+Eyl2=1088 J
(6)第七阶段。第七阶段为点D到点E的负载移动过程,该过程Z轴移动元动作能耗描述函数如图9所示,换元后得Pxl(t)如下:

图9 元动作X负载功率曲线
Pxl(t)=-2.8×104(0.376+0.161t)3+
2.3×104(0.376+0.161t)2-
4.6×103(0.376+0.161t)+300
代入式(7)得能耗为

(7)第八阶段。第八阶段为点E到点F的负载移动过程,该过程Z轴移动元动作的能耗描述函数如图10所示。换元后得Pzl(t)如下:

图10 元动作Z负载功率曲线
Pzl(t)=-2.1×104(0.332-0.161t)4+1.3×104(0.332-0.161t)3-2.4×103(0.332-0.161t)2+1.8×102(0.332-0.161t)+318
代入式(7)得能耗为

(8)第九阶段。第九阶段为点F处静态待机,该处静态元动作功率为322 W,运行时间为4 s,故此处静态元动作的能耗如下:
Es2=322×4=1288 J
综上,可得移动元动作空载过程总能耗Emu、移动元动作负载过程总能耗Eml和静态元动作总能耗Es如下:
Emu=Eyu+Ezu=1003 J
Eml=Ezl++Eyl+Exl+Ezl-=2333 J
Es=Es1+Es2=29 317 J
综上,总能耗的预测结果如下:
E=Es+Emu+Eml=32 653 J
4.3 讨论
为了验证预测精度,本实验还对各阶段能耗及总能耗进行了试验测量获取,各阶段的能耗测量结果见表2,总能耗为33 068 J。预测结果与测量结果相差为415 J,误差为1.3%,预测精度较高。
本文方法在工作量与准确度方面与现有能耗预测方法的区别见表3。可知,本文预测时需获取的参数较少,在工作量方面具有一定的改进作用;而在准确度方面,从影响因子数量和案例结果来看,与现有方法是相当的。

表3 能耗预测方法对比
5 结论
(1)本文提出了工业机器人元动作及元动作库概念,并建立了元动作的能耗描述函数模型。
(2)建立了基于元动作的工业机器人能耗预测方法,应用该方法,只需离线测试元动作功率并建立能耗描述函数,便能实现目标过程的能耗预测。
(3)开展案例研究,验证了所提方法的可行性与实用性。
本文所建模型适用于由X,Y,Z移动或转动构成的全运行过程能耗预测,而对于包含空间任意圆弧运动的复杂运动过程,还有待进一步研究,这也是本课题组今后主要的研究方向。
