运动学约束下直线转角非对称平滑加工规划
2022-11-25何昱龙琚长江杨根科王成光
何昱龙 琚长江 杨根科 王成光
1.上海交通大学宁波人工智能研究院,宁波,315000 2.上海交通大学自动化系,上海,200240 3.宁波工业互联网研究院,宁波,315000
0 引言
高速高精度加工一直是现代计算机数控系统亟待解决的问题,平滑的刀具路径和进给速率是实现所需加工质量的关键。在计算机辅助设计系统中,可以使用非均匀有理B样条曲线等光滑样条插补曲线来描述刀具轨迹[1],计算机辅助制造系统常直接采用直线段(G01)拟合逼近曲线的方式输出刀具轨迹[2-4],零件的几何外形也可能包含带有转角的长直线段刀具轨迹。直线段刀具轨迹在转角处仅考虑了位置连续,忽略了速度与加速度的连续变化,在零件加工时,刀具在转角处必须完全停止以避免驱动器因超过机械极限而引起惯性振动、破坏零件表面光洁度,导致加工效率低。
为平滑G01刀具轨迹,实现不间断的连续运动,目前主要有两种方法:全局平滑[5-6]与局部转角平滑[2-4,7-12]。全局平滑将所有线性轨迹进行拟合,生成连续参数刀具轨迹,计算量大[3]且难以评估平滑过程中产生的误差;局部转角平滑使用指定的参数曲线在定义的公差范围内混合相邻的线段,计算量小,有利于误差评估与实时计算。
一般局部转角平滑研究[2-4]会分离几何误差约束与运动学约束,使平滑过程主要分成两步:先插入参数曲线,然后规划运动轨迹。这种方法仅考虑切向运动限制,造成执行器大量性能损失,并且参数曲线的弧长难以解析,用弦长代替弧长会引入额外误差造成速率波动。为解决此问题,近年来出现一种不需要参数曲线拟合的转角轨迹平滑方法,该方法在刀具轨迹平滑规划的同时进行运动轨迹规划。TAJIMA等[8]提出了两种基于运动学的转角平滑规划方法,并在文献[6]中加以优化,生成了加加速度限制下的加速度不间断转角平滑轨迹。一般情况下,G01转角开始和结束所在直线运动学约束并不相同,TAJIMA等[6]提出的转角平滑方法基于直线转角运动开始与结束时进给速率与加速度大小相同的对称假设,无法充分利用执行器性能。为此,ZHANG等[9]提出了一种直接生成非对称时间最优的转角平滑轨迹方法,但忽略了加速度的突变。WANG等[11]提出了基于整体加工时间优化的非对称转角平滑规划方法,相比文献[8]可以取得更好的效果,但在求解过程中需要多次迭代,不适用于实时计算转角平滑轨迹生成。ZHANG等[10]提出了一种直线段进给速率混合的方法,实现了非对称的转角平滑规划,但转角处加加速度的约束过强制约了执行器性能的发挥。
本文对可以达到给定进给速率的平面G01刀具轨迹进行了研究。在S型速度轨迹规划的前提下,通过对转角处运动学和几何误差约束的分析,提出一种直线转角的非对称平滑规划方法,实现进给速率与刀具轨迹的同时规划,利用轴向加加速度与误差约束解算准时间最优的刀具轨迹转角平滑参数。
1 单轴初末速度、加速度不为零的S型速度轨迹规划
S型速度轨迹规划又称加加速度限制速度轨迹规划,引入了加加速度限制使加速度连续,从而使速度轨迹具有柔性,有效抑制运动中的残余振动[12-13]。完整的S型速度规划分为以下7个阶段:加速度增加阶段(Ⅰ阶段)、加速度恒定阶段(Ⅱ阶段)、加速度减小阶段(Ⅲ阶段),速度(速率)恒定阶段(Ⅳ阶段)、减速度增加阶段(Ⅴ阶段)、减速度恒定阶段(Ⅵ阶段),减速度减小阶段(Ⅶ阶段),如图1所示。其中,阶段Ⅰ、Ⅱ和Ⅲ统称加速阶段,阶段Ⅴ、Ⅵ、Ⅶ统称减速阶段。
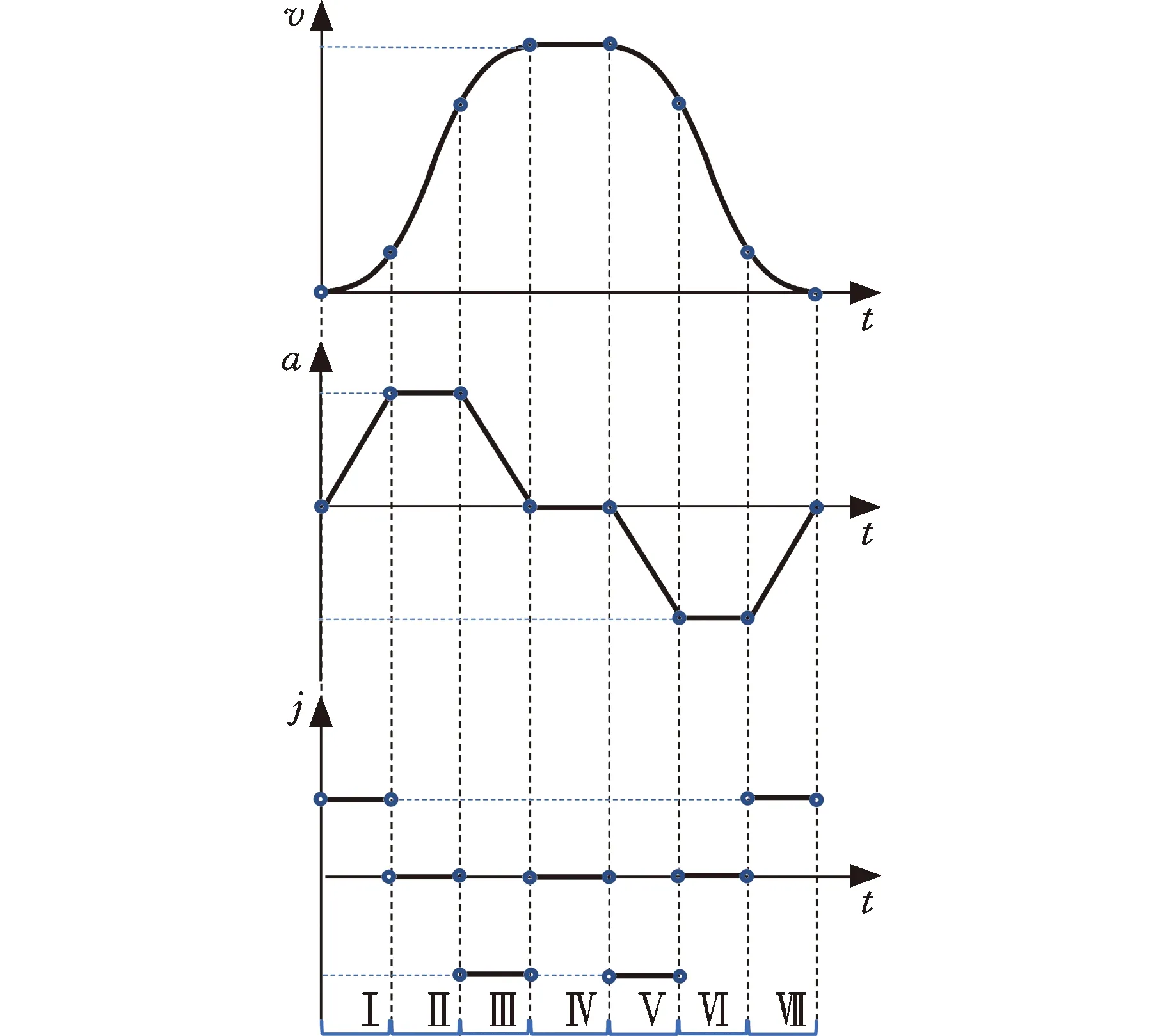
图1 七段式S型速度轨迹
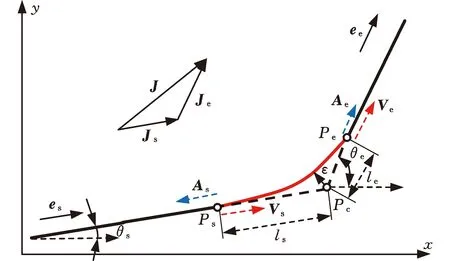
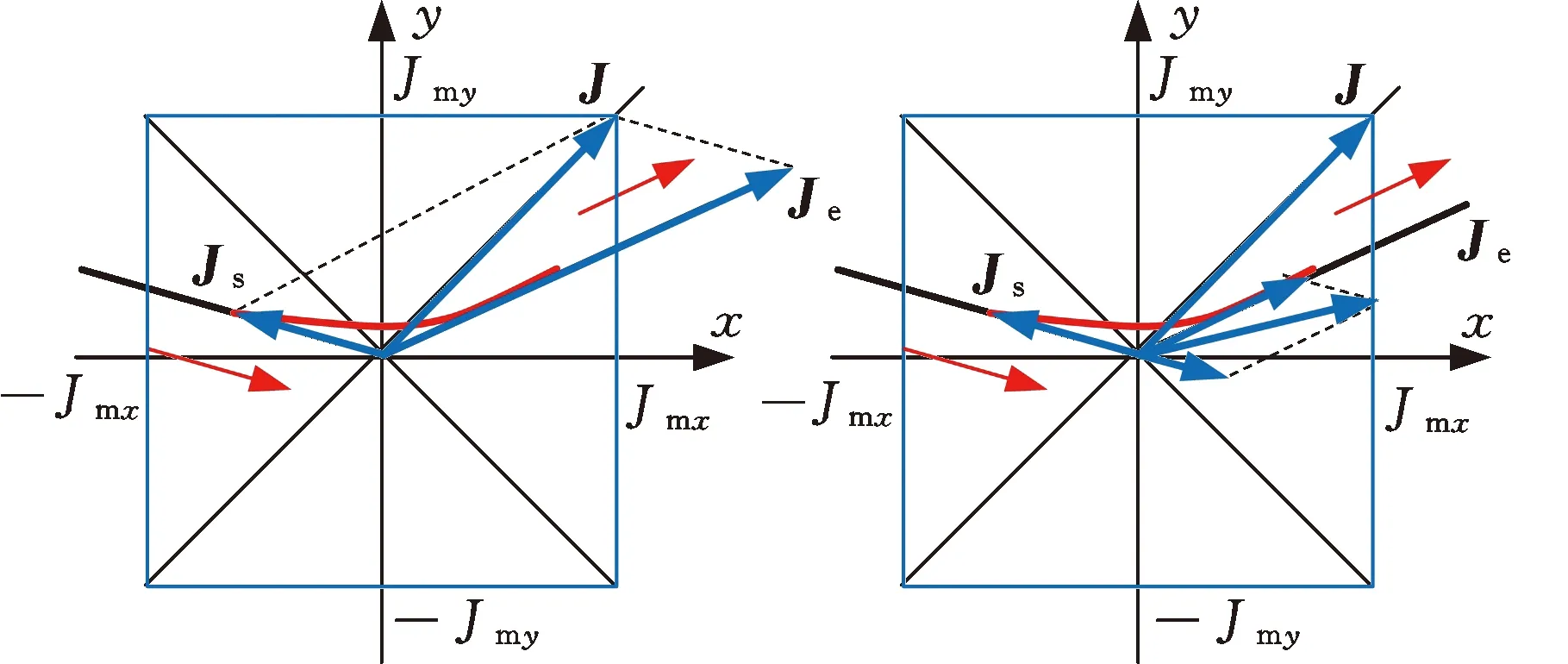
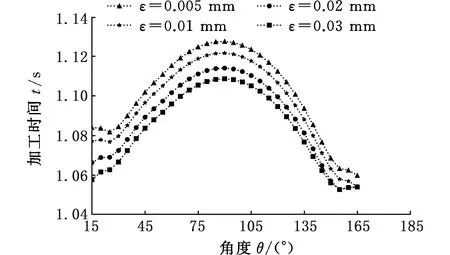
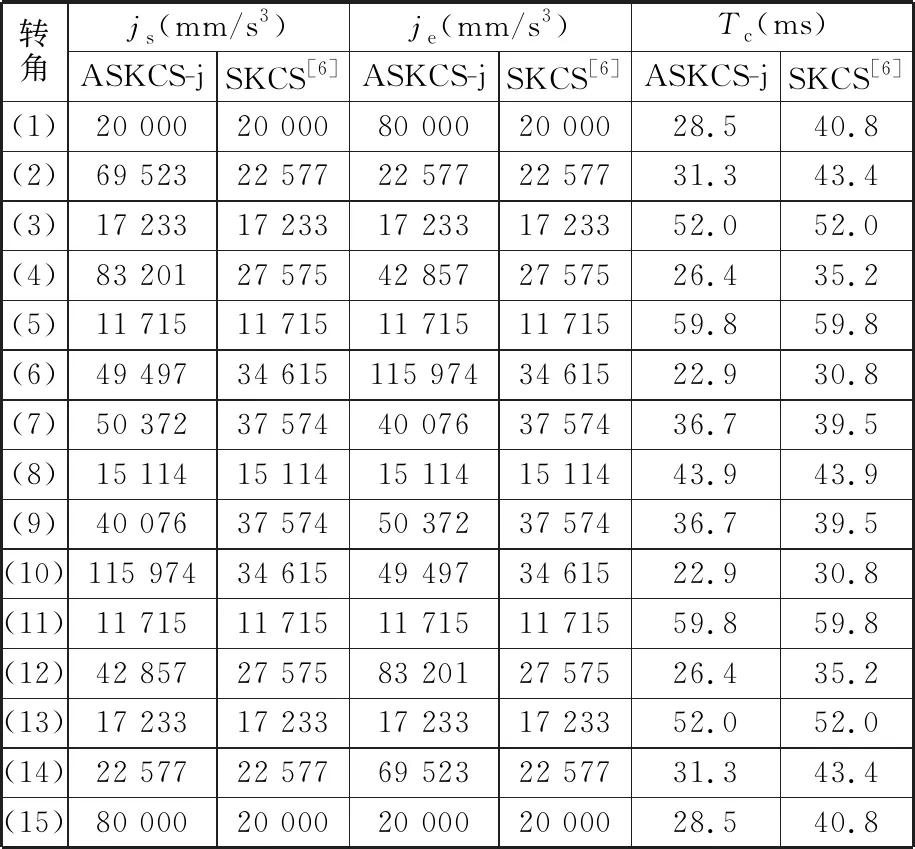
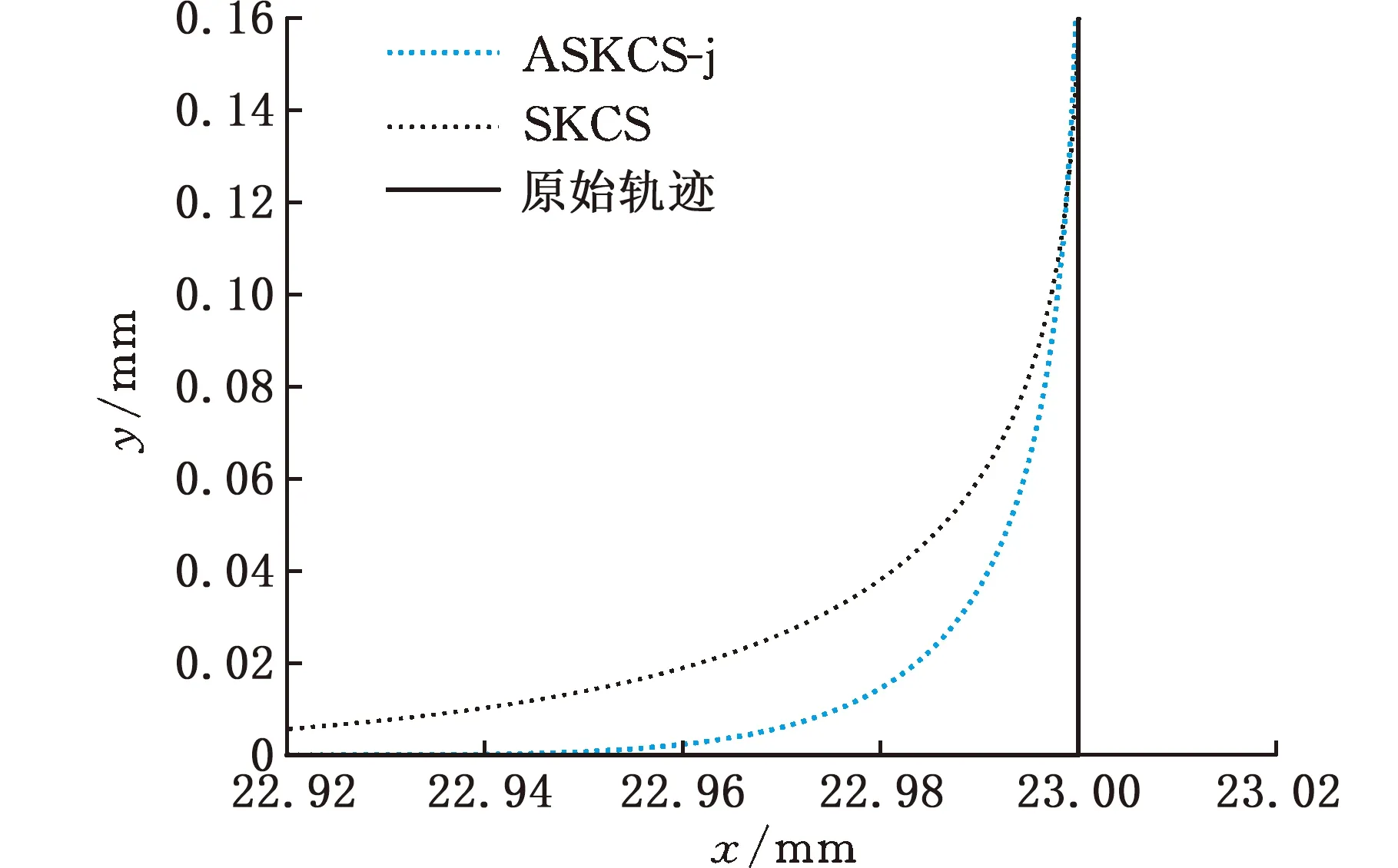
在初末速度、加速度不为零的运动中,系统给定最大速度为vmax,最大加速度为amax,最大加加速度为jmax,则运动过程可描述为从给定开始速度vs(0 主要分析加速段(Ⅰ、Ⅱ、Ⅲ)的运动轮廓,从vs(vs 图2 四种加速段情况 首先给出阶段Ⅰ、Ⅱ、Ⅲ均存在的加速段加加速度、加速度和速度的运动轨迹方程: (1) (2) (3) v2=v1+amaxT2a 式中,J(t)、A(t)、V(t)分别为t时刻的加加速度、加速度、速度;i=Ⅰ,Ⅱ,Ⅲ表示不同的运动阶段;τi=t-ti,ti为第i阶段的结束时间;Tia为第i阶段的持续时间;vi为第i阶段结束时的速度。 下面介绍各时间段的求解方法。加速段速度差值Δv=vmax-vs,定义Δvf为as以最大加加速度直接减为0时速度的改变量,即满足 (4) 当Δv=Δvf时,仅阶段Ⅲ存在,则有 T1a=T2a=0T3a=as/jmax (5) 当Δv<Δvf时,加速度先减小后增大,加速段不存在此情况;当Δv>Δvf时,T2a存在的条件为 若as (6) 当as=amax时,阶段Ⅱ、Ⅲ存在,T1a=0,T2a、T3a的计算公式同式(6)。 (7) T1a、T3a分别为 (8) 减速段同理,不再赘述。作为特例,初末速度加速度为零的S型速度轨迹规划,可令vs=ve=as=ae=0获得。 经过不同直线段的相交处时,允许转弯速度不完全减为零,以减少电机的频繁启停,提高运动效率。 如图3所示,两直线交点为Pc,es和ee分别表示两条直线上运动方向的单位向量,θs和θe分别为两向量与x轴正向夹角;ε为给定的转角点Pc到转角平滑曲线的最大容许误差;Ps和Pe分别为转角平滑运动的开始点与结束点,Vs、As分别为开始点处的速度与加速度,大小为Vs、As,PsPc为开始点到转角点的位移,长度为ls;Ve、Ae分别为结束点处的速度与加速度,大小为Ve、Ae;PcPe为转角点到结束点的位移, 长度为le;J为转角平滑时的加加速度,J=Js+Je=jses+jeee,Js、Je分别为J在es和ee方向上的投影,大小为js、je。在单次直线转角平滑过程中,js与je保持不变。可写为 图3 直线转角的非对称平滑规划轨迹示意图 (9) 在转角平滑运动过程中,其矢量运动学方程可写为 (10) 其中,τ∈[0,Tc];Tc为直线转角平滑过程的持续时间;Aτ、Vτ、Sτ分别为τ时刻的加速度、速度与位移;Vτs、Vτe分别为τ时刻Vτ在es和ee上的分量。τ时刻的矢量合成图见图4。 图4 直线转角非对称平滑规划中运动学矢量合成示意图 当τ=Tc时,转角平滑运动结束。将τ=Tc代入式(10),并将以上运动学矢量分别向es和ee方向投影,联立式(9)可获得转角平滑运动的边界处参数ls、le、As、Ae、Vs、Ve与js、je、Tc的关系: (11) 在转角平滑的运动过程中,任意τ时刻到Pc距离的平方为 (12) 设τε时刻为转角运动平滑过程中距离Pc最近的时刻,则有 ‖PcPτ‖2≥‖PcPτε‖2 (13) 提高最大容许误差有利于提高加工效率[8,11],故令‖PcPτε‖2=ε。由于τε的计算过程复杂,故基于式(12)和式(13)的特殊形式,选择τ=Tc/2处的轨迹点与Pc的距离为最大容许误差的边界值,即‖PcPTc/2‖2=ε,这保证了转角平滑轨迹在规定的误差范围内,即 ‖PcPτε‖2≤‖PcPTc/2‖2=ε (14) 基于式(12)与式(14),可用js、je对Tc进行解析表示,即 (15) 联立式(14)与式(17),可通过js、je两个决策参数对直线转角平滑的运动轨迹进行描述。 一般情况下,在平面的直线运动中,由于需要对x、y轴的速度进行耦合,为实现准时间最优,仅能达到单轴运动学极限,此时有 (16) 式中,Ams、Ame分别为转角开始与结束所在直线段的直线运动中的加速度边界;Jms、Jme为加加速度边界;Amx、Amy分别为x轴与y轴的轴向加速度极限;Jmx、Jmy为轴向加加速度极限。 在转弯过程中,可能同时达到x、y轴的加加速度极限,即 (17) 由于Vs与Js同向,Ve与Je同向,且在加工过程中,速度方向恒为正向,则有 js>0je>0 (18) 为确定转角平滑时的运动轨迹,需要确定js、je,即针对式(17)的求解。随着θs与θe的变化,在式(18)的约束下,式(17)的解出现无解、单解、双解三种情况,在无解情况下需要进行修正,此时仅能满足单轴加加速度极限。三种情况对应的轴向加加速度分解如图5所示。 (a)无解 (b)无解修正 为求解js、je,并充分利用x轴与y轴的轴向加加速度极限,本文采用以下两种优化模型。 (1)模型1。基于速度的非对称运动学直线转角平滑(velocity-based asymmetrical kinematics corner smooth,ASKCS-v),即最大化直线转角开始与结束时的进给速率和: max(Vs+Ve) (20) 注意到此约束中存在等式,且Vs、Ve和Tc均可由js和je表示,可将模型简化为 (21) (2)模型2。基于加加速度的非对称直线转角平滑(jerk-based asymmetrical kinematics corner smooth,ASKCS-j),即最大化直线转角开始段与结束段的加加速度较小值: (22) 在转角处,不需要多轴的耦合,为了实现加速度的连续变化,仍需要对加速度进行单轴极限的限制,即 (23) 其中,A′ms、A′me分别为开始与结束所在直线段的直线运动中可达到的最大加速度,F为最大进给速率。若超过约束,则重新修正转角时间: (24) 在转角平滑的过程中,由于最大容许误差的存在,转弯处的允许进给速率较小,一般无法达到给定的进给速度,如果转角钝化严重,即|θe-θs|趋近于180°,出现Vs>F,在这种情况下,令Vs=Ve=F,As=Ae=0,根据文献[8]所述方式在转角处进行平滑规划。 ASKCS-v(模型1)包含高次项,采用序列最小二乘规划算法进行迭代求解。 ASKCS-j(模型2)为简单的线性规划问题,最优解存在于边界,求解步骤如下: (1)求解式(17)可得4个坐标点(jsi,jei),i=1,2,3,4。 (3)令mini=min(jsi,jei),i=0,1,…,4,记k为{mini}中最大值的下标,(jsk,jek)即目标解,结束。 两种优化模型均旨在获得转角处的最大进给速率以满足速度规划中的准时间最优。ASKCS-v优化模型纳入对Tc的考虑,进一步约束了转角平滑过程;ASKCS-j为简单的线性规划问题,求解简单,有利于进行转角平滑轨迹的实时规划。 首先在单转角刀具轨迹中对比ASKCS-v与ASKCS-j在各种转弯角度下的性能表现,然后在连续转角刀具轨迹中将ASKCS-j与文献[6]中的对称转角平滑(symmetrical kinematics corner smooth,SKCS)算法进行对比。 两条直线段P0P1和P1P2构成的单转角刀具轨迹如图6a所示,两条直线段长度均为40 mm,最大进给速率Fm=100 mm/s,规定运动状态为从P0处完全静止(速度与加速度均为0)开始到P2处完全静止结束,P1P2与x轴正向的夹角从15°到170°变化。对比了ASKCS-v与ASKCS-j在最大容许误差ε=0.02 mm的情况下,给定不同轴向加速度与轴向加加速度极限(具体数值在图6a中已给出)的加工时间,并将文献[10]的进给速率混合(feedrate blengding method, FBM)和运动在转角处完全静止(point to point, PTP)的运动规划方法纳入对比,仿真结果如图6b~图6f所示。对比了ASKCS-j在Amx=1 m/s2,Amy=2 m/s2,Jmx=20 m/s3,Jmy=10 m/s3的条件下,不同最大容许误差(具体数值图中已给出)约束下的加工时间,结果如图7所示。 (a)单转角刀具轨迹 (b)Amx=1 m/s2 ,Amy=1 m/s2Jmx=10 m/s3,Jmy=10 m/s3 (c)Amx=1 m/s2,Amy=2 m/s2Jmx=10 m/s3,Jmy=20 m/s3 图7 不同误差约束下ASKCS-j单转角加工时间对比 由图6b~图6f可看出,相比PTP的规划方法,FBM、ASKCS-v与ASKCS-j在加工时间上均有减少,当两直线夹角为锐角时,ASKCS-v与ASKCS-j可以节省更多的加工时间;在加工时间方面,ASKCS-v在锐角情况下略优于ASKCS-j,但在求解速度方面,ASKCS-j明显快于ASKCS-v,在工程上可进行实时的转角平滑规划。由图7可看出,当最大允许误差增大时,加工时间缩短,这是由于提高最大允许误差可以实现更大的进给速率通过转角。最大允许误差的存在,柔滑了直线夹角,实现了加工过程中速率、加速度的连续性。 将ASKCS-j与SKCS用于图8所示的“枫叶”刀具轨迹的转角平滑中,并对结果进行了比较分析。“枫叶”刀具轨迹设有不同角度的转弯,且路径存在对称性,有利于考察转角平滑算法的综合性能。 图8 “枫叶”刀具轨迹 “枫叶”轨迹中的运动学约束与最大允许误差见表1;“枫叶”轨迹的坐标与在直线运动中的运动学边界见表2;两种平滑规划方法在各转角处的运动参数见表3;加工完给定的“枫叶”刀具轨迹的整体加工时间和在各转角处最大误差的平均值见表4;部分转角处的平滑轨迹如图9所示。“枫叶”刀具轨迹中的运动学轨迹曲线(局部)如图10所示。 表1 “枫叶”刀具轨迹中的约束 表2 直线段坐标及直线运动中的运动学边界 表3 转角处的运动参数 表4 加工时间与转角误差平均值 (a)转角(1) (a)进给速率 上述仿真结果表明,基于两种模型的规划方法均将轴向加加速度约束在给定范围内,实现了进给速率与轴向加速度的连续变化;相比SKCS,本文提出的ASKCS-j在转角处更能充分利用执行器的性能,缩短运动时间,获得更平滑的轨迹,将刀具轨迹的整体加工时间缩短了2.3%,最大误差平均值减小了13%。可见,ASKCS-j可以在运动学与几何误差约束下提供更准确的轨迹,并能提供更短的加工时间,满足高速高精度加工需求。 为验证ASKCS-j方法的有效性,搭建了图11所示的运动控制实验平台,该平台主要采用倍福twincat3运动控制软件、三菱PLC和松下伺服驱动器和伺服电机(型号MINAS-A6B)。 图11 实验平台实物图 设定系统参数,进给速度最大为100 mm/s,允许最大误差为0.04 mm,x轴与y轴的加速度与加加速度分别为Amx=2 m/s2,Amy=2 m/s2,Jmx=50 m/s3,Jmy=50 m/s3。加工实验轨迹参考图见图12a,实际加工情况如图12b所示;仿真进给速率变化如图12c所示,实际加工过程中的进给速度图见图12d。 (a)实验参考轨迹 (b)实际加工情况 如图12c、图12d所示,ASKCS-j仿真过程的整体运动时间为7.52 s,实际运动的时间为7.74 s,仿真结果与实际结果在运动速度、运动时间存在差距,这是由于实际的运动系统为离散系统,针对连续系统进行采样的周期固定,造成部分数据点丢失;同时在运动过程中存在实际惯量、摩擦等多方面物理因素,造成运动过程的抖动,但仿真结果与实际结果差距在一定的范围内,可以认为实际结果与仿真结果相同。因此,本文方法保证了加工过程中进给速率的连续变化,并实现了转角过程中进给速率不完全减为0,减少电机的频繁启停,提高了加工效率。 本文针对直线段刀具轨迹的非对称转角平滑规划进行研究,通过运动学分析提出了一类两种指标下可解析的加加速度有限的直线转角非对称平滑规划方法,通过仿真实验与样机实验验证了该类方法的可行性与有效性。该规划方法可以同时实现进给速率与刀具轨迹的平滑规划,获得连续变化的进给速率和轴向加速度变化曲线;充分利用驱动器的性能,无需迭代直接解析转角平滑时的轨迹参数,得到更好的、非对称的转弯平滑轨迹,相比对称转角平滑规划,本文方法具有更小的误差和更短的加工时间的优点,能够满足高速高精度加工的需求。本文方法以两轴平面直线加工为研究基础,可推广到笛卡儿坐标系下任一平面的直线加工,三轴及三轴以上的加工也可考虑采用本文方法。
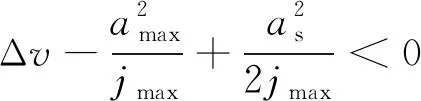
2 平面直线转角非对称平滑规划建模
2.1 直线转角的非对称平滑规划轨迹

2.2 非对称直线转角平滑规划参数的确定

3 优化模型求解

4 仿真分析与实验验证
4.1 单转角对比分析

4.2 连续转角对比分析





4.3 样机实验验证


5 结语
