四轮驱动电动汽车质心侧偏角与轮胎侧向力非线性鲁棒融合估计

王凡勋 殷国栋 沈 童 任彦君 汪 冯 斌

东南大学机械工程学院，南京，211189

0 引言

四轮驱动电动汽车是以轮毂电机为动力单元，融合独立驱动、制动的电动汽车，已被国际汽车领域专家认为是最具发展潜力的架构之一[1]。汽车电动化、网联化、智能化、共享化成为汽车行业发展的未来趋势和当前行业瓶颈的重要突破口，因此，智能驾驶车辆已成为国内外研究人员和工程师的研究热点[2]。四轮驱动电动汽车相对于传统的集中式电动汽车具有更高的控制维度，建设智能车辆平台的难度更高，持续发展的车辆运动控制和主动安全技术更为迫切地需要实时精确地获取车辆相关状态参数[3]，因此精准估计关键车辆状态参数成为四轮驱动电动汽车智能化发展的“卡脖子”问题。

在建设四轮驱动电动汽车智能化平台的过程中，由于相关传感器成本过高或一些车载传感器不能直接获取车辆状态参数(质心侧偏角和轮胎侧向力均存在此类问题)，因此，掌握准确获取质心侧偏角与轮胎力的技术尤为重要[4]。四轮驱动汽车由轮毂电机驱动，转矩可精确获得，轮胎的纵向力可直接计算得到，因此，质心侧偏角和轮胎侧向力的估计成为国内外研究热点[5]。质心侧偏角的观测方法主要包括扩展卡尔曼滤波[6]、龙贝格观测器[7]、滑膜观测器[8]、无迹卡尔曼滤波[9]、鲁棒观测器[10]等估计方法，轮胎侧向力估计的方法主要包括神经网络方法[11]、卡尔曼滤波[12]、交互多模型滤波[13]等估计方法，由此可见卡尔曼滤波是车辆质心侧偏角和轮胎侧向力的主流估计算法。

WILKIN等[14]基于3自由度车辆模型提出了扩展卡尔曼滤波作为轮胎侧向力的估计器，通过试验证明此估计方法可获得良好的估计精度，但由于扩展卡尔曼滤波是基于泰勒展开式一阶近似的，估计精度还不够理想。DOUMIATI等[15]基于四轮车辆模型进行质心侧偏角和轮胎侧向力的估计，对比了扩展卡尔曼滤波和无迹卡尔曼滤波这两种估计方法，无迹卡尔曼具有二阶精度的近似，通过仿真试验证明无迹卡尔曼比扩展卡尔曼估计精度更高。JIN等[16]提出一种交互多模型的无迹卡尔曼滤波方法对轮胎侧向力和质心侧偏角进行估计，考虑到车辆在实际行驶过程中驾驶环境的改变，采用基于交互多模型车辆状态估计方法通过随机过程对合适的车辆模型进行加权以匹配相应的驾驶环境，虚拟仿真试验表明，相比于单一模型的方法，所提方法能够提供更准确的车辆状态估计，但对无法覆盖的工况适应性较差，且算法较为复杂，实车的应用难度大。刘刚等[17]基于平方根容积卡尔曼滤波算法对车辆质心侧偏角和轮胎侧向力进行估计，虽然估计算法已达到三阶精度，但由于没有考虑模型的参数摄动和未知输入，估计结果受模型参数摄动的影响较大从而导致估计精度较低。考虑车辆实际行驶过程可能包括系统未建模的动态特性、模型参数摄动、系统过程噪声以及测量噪声等因素影响估计结果的准确性，估计算法必须提高估计过程中对模型参数摄动以及未建模噪声的抗干扰能力，解决复杂工况下的异源传感器信息融合问题。

为了提高质心侧偏角和轮胎侧向力估计的准确性、可靠性和工况适应性，本文提出了一种基于遗忘因子递归最小二乘法(forgetting factor recursive least square, FFRLS)与鲁棒容积卡尔曼滤波(robust cubature Kalman filter, RCKF)的联合估计方法。首先建立包括车辆纵向、侧向和横摆三自由度的四轮驱动电动汽车动力学模型，引入可反映轮胎瞬时力学特性的半经验魔术轮胎模型；其次根据车辆的纵向动力学平衡方程，考虑车辆行驶过程中的纵向空气阻力和轮胎滚动阻力，基于带有遗忘因子的递归最小二乘法对整车质量进行了实时估计；再次，在鲁棒容积卡尔曼滤波的架构下构建了车辆动力学信息融合模型对质心侧偏角和轮胎侧向力进行实时估计，基于最小化最大估计误差协方差实现算法设计，提高估计算法的鲁棒性；然后在CarSim/Simulink的环境下进行联合仿真,验证了方法的有效性，并和其他几种方法进行了对比；最后为验证算法的收敛性、准确性和鲁棒性，在四轮驱动电动汽车实车平台进行验证，讨论了所提算法在面对不同工况时估计的准确性。

1 四轮驱动电动汽车动力学模型

本文针对四轮驱动电动汽车，建立包括纵向、侧向和横摆的三自由度的四轮非线性车辆模型。建立的四轮车辆动力学模型如图1所示，其中，车辆前进方向为坐标系X轴正方向，驾驶员左手方向为坐标系Y轴正方向，垂直地面向上方向为坐标系Z轴正方向，根据右手定则确定旋转运动正方向。

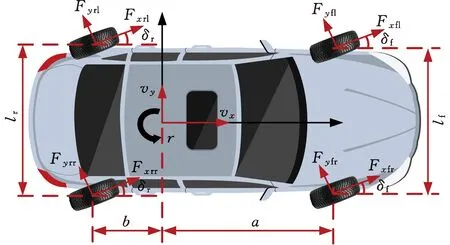
图1 车辆动力学模型

针对所建立的非线性四轮车辆模型，作如下假设：①假设车辆是对称的，估算车辆模型质心处的坐标系OXY与车辆坐标系原点重合；②忽略车辆行驶过程中的俯仰、侧倾、悬架及转向系统等影响；③假设转向系统调教准确，左侧和右侧前轮转角相等。

根据达朗伯原理，整车的动力学方程如下：

(1)

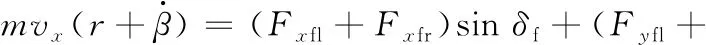
(2)

max=(Fxflcosδf-Fyflsinδf)+(Fxfrcosδf-
Fyfrsinδf)+Fxrl+Fxrr-Fw-Ff

(3)

may=(Fxflsinδf+Fyflcosδf)+(Fxfrsinδf+
Fyfrcosδf)+Fyrl+Fyrr

(4)

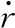
车辆所受的纵向空气阻力Fw和轮胎的滚动阻力和Ff计算公式分别为[18]

(5)

Ff=frmg

(6)

式中，Cd为空气阻力系数；ρ为空气密度；Af为车辆正面迎风面积；fr为滚动阻力系数；g为重力加速度。

轮胎侧向力与轮胎侧偏角和垂向载荷有关，故各轮的轮胎侧偏角和垂向载荷分别为

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

式中，Fzij为轮胎垂向载荷；αij为轮胎侧偏角；h为质心到地面的高度。

四轮驱动电动汽车以轮毂电机为动力单元，可以进行单轮的驱动/制动，轮毂电机具有转矩、转速等精确可知的特点，因此可以直接计算轮胎的纵向力，车轮的动力学方程为

(15)

式中，Tij为电机转矩；J为车轮转动惯量；ωij为车轮的转动角速度；Rw为轮胎滚动的有效半径。

根据半经验魔术轮胎公式来计算轮胎的侧向力，轮胎侧向力的计算表达式可写成

Fyij=Dsin[Carctan(Bαij-E(Bαij-arctanBαij))]

(16)

式中，B为刚度因子；C为曲线形状因子；D为峰值因子；E为曲线曲率因子。

上式所建立的非线性轮胎模型仅适用于准稳态工况，此理想工况下轮胎模型无法反映车辆运动过程中轮胎瞬时的运动力学状态，当轮胎侧偏角、车轮垂向载荷和车辆速度发生改变时，运动过程中轮胎力的变化存在相对的时滞。因此，根据已建立的稳态轮胎模型，以半物理半经验的方式引入松弛长度来表示非线性轮胎模型的非稳态效应，对稳态轮胎模型进行适当修正，可得表征轮胎瞬时特性的非线性动态轮胎模型公式[19]：

(17)

式中，σij为松弛长度。

2 基于遗忘因子RLS法的质量估计

递归最小二乘法(recursive least square, RLS)采用最小二乘法(least square, LS)的准则，其原理是采用指数加权的误差平方和极小化模型估计误差，RLS算法具有较好的收敛性和跟踪能力，且计算量小[20]。遗忘因子可以进一步调整估计过程中新数据的权重，提高算法的适应性。质量估计是下一步车辆质心侧偏角和轮胎侧向力估计的前提，很大程度上影响了车辆状态估计的准确性。本文的车辆质量估计过程应用在车辆刚起步的阶段，此时轮胎侧偏角很小，故轮胎侧向力可以忽略不计，考虑车辆的纵向动力学平衡方程(式(3))，根据遗忘因子RLS法建立质量估计输入输出递归方程：

y(k)=h(k)Tθ+e(k)

(18)

式中，h(k)为输入量，为可测量的数据向量；y(k)为系统的输出量；θ为待估参数，本文待估计参数为整车质量m。

由纵向动力学方程可得

(19)

带有遗忘因子的递归最小二乘法步骤如下：

(1)求解参数辨识增益：

(20)

(2)更新参数辨识：

(21)

(3)更新辨识误差：

(22)

式中，K(k)为k时刻的参数辨识增益；P(k)为k时刻的协方差矩阵；I为单位矩阵；λ为遗忘因子。

3 质心侧偏角和轮胎侧向力估计算法

本文将极大值背景下的估计误差最小化嵌入标准容积卡尔曼滤波算法(cubature kalman filter, CKF)以实现鲁棒容积卡尔曼滤波对质心侧偏角和轮胎侧向力的联合估计，将上节实时估计的整车质量作为实时更新的输入值。本节通过可直接测量的纵向和侧向加速度、前轮转角、纵向车速及横摆角速度，并利用轮毂电机转矩精确可知的特点，根据轮胎动力学模型直接计算轮胎纵向力，在复杂工况下通过异源传感器信息融合准确估计质心侧偏角和轮胎侧向力。

3.1 非线性车辆模型状态空间

根据式(1)～式(17)，建立车辆质心侧偏角和轮胎侧向力的状态方程和观测方程：

(23)

状态变量、输入变量、观测变量分别为

x(t)=(r,β,Fyfl,Fyfr,Fyrl,Fyrr)T

(24)

u(t)=(δf,vx,Fxfl,Fxfr,Fxrl,Fxrr)T

(25)

z(t)=(ax,ay)T

(26)

推导出估计算法的非线性状态方程函数f(·)和观测方程函数h(·):

f(·)=(f1,f2,…,f6)

(27)

h(·)=(h1,h2)

(28)

根据四轮驱动电动汽车动力学模型，函数表达式f(·)和h(·)分别可写成

(29)

(30)

3.2 鲁棒容积卡尔曼滤波算法设计

对式(23)状态方程和观测方程进行离散化，可得

(31)

其中，xk为系统的状态向量，xk∈Rn；uk为已知的控制输入，uk∈Rm；zk为系统的观测向量，zk∈Rp；函数f:Rn×Rm→Rn和h:Rn×Rm→Rp分别为已知的非线性函数；wk、vk分别为系统的过程噪声和观测的测量噪声，两者为高斯白噪声且互不相关，服从正态分布：wk～N(qk,Qk)，vk～N(rk,Rk)；初始状态x0与wk、vk互不相关。

(1)初始化。令

(32)

(33)

(2)时间更新。对k-1时刻的误差协方差矩阵Pk-1|k-1进行分解：

(34)

根据球面径向规则计算容积点：

(35)

式中，L=2n,n为待估状态的维数。

计算状态方程传播的容积点：

(36)

计算状态估计值：

(37)

计算估计误差协方差矩阵：

(38)

(3)测量更新。对更新之后的误差协方差矩阵Pk|k-1进行分解：

(39)

计算更新的容积点：

(40)

计算测量方程传播的容积点：

(41)

估计观测预测值：

(42)

计算新协方差矩阵：

(43)

计算估计协方差矩阵：

(44)

设计H∞滤波器需要将统计线性化方法应用于状态方程和测量方程，将容积卡尔曼算法转换为线性回归形式[21]。

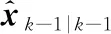
(45)

(46)

估计卡尔曼增益：

(47)

估计状态更新：

(48)

估计相应误差协方差：

Pxx,k|k=Pxx,k|k-1-{[Pxz,k|k-1Pxx,k|k-1]×

(49)

(50)

(51)

式中，η为调节因子，调节最小均方根和H∞滤波的性能；eig(·)为求解特征值函数。

因此，η可取

(52)

其中，λ>1。综上，得到最终质心侧偏角和轮胎侧向力估计算法实时方案的结构框图，见图2。

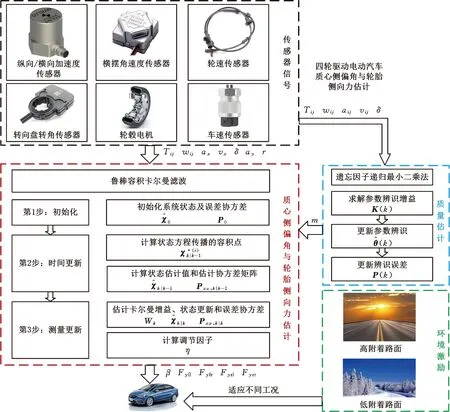
图2 联合估计算法实施方案

4 虚拟试验仿真验证与分析

为验证本文提出的联合估计算法(FFRLS+RCKF)的有效性，在CarSim/Simulink的环境下进行联合仿真试验与分析，CarSim和Simulink之间的通信通过CarSim-S函数的接口来实现。为了说明FFRLS+RCKF算法的准确性、鲁棒性及适应性，根据GB/T 6323—2014《汽车操纵稳定性试验方法》，选取蛇形试验作为虚拟试验仿真的试验工况，蛇形试验具有典型性和代表性。分别设置不同的路面附着系数，在不同工况下对比了鲁棒容积卡尔曼滤波(RCKF)与标准容积卡尔曼滤波(CKF)[23]，并对试验结果进行分析。四轮驱动电动汽车底盘参数见表1。

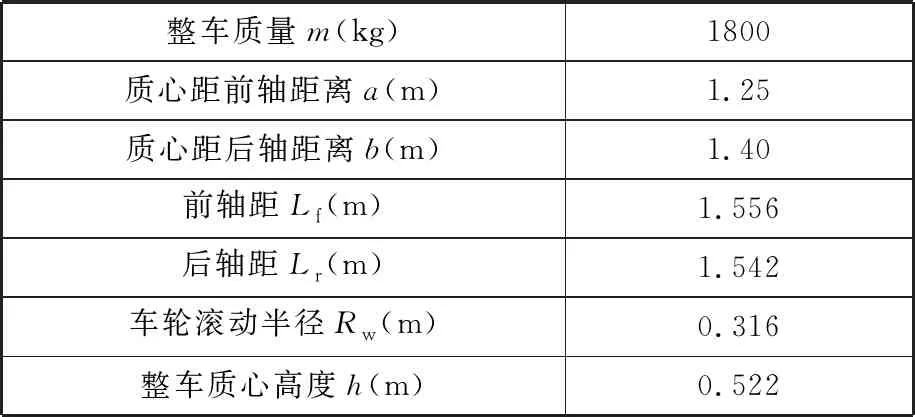
表1 四轮驱动电动汽车底盘参数

4.1 高附着路面仿真试验与分析

仿真环境设置如下：在附着系数为0.8的路面上进行蛇形仿真试验，前轮转角的变化如图3所示，初始车速设置为30 km/h，行驶过程施加总驱动力为500 N，采样时间为1 ms，纵向和侧向加速度变化如图4所示。过程噪声协方差矩阵Q为I6×6，观测协方差R的值为0.1。

图3 前轮转角输入(高附着路面)

图4 纵向和横向加速度(高附着路面)

基于带有遗忘因子的递归最小二乘法估计整车质量算法中，整车质量估计初值设为1000 kg，由表1可知，真实值为1800 kg，遗忘因子λ设为0.97，FFRLS算法估计结果和真实值对比如图5所示。

图5 整车质量估计值与真实值(高附着路面)

由图5可见，基于FFRLS算法的质量估计过程中，起始时刻曲线在真实值附近出现小幅波动，在1 s内可以实现对真实值的较好跟踪，且后面的估计过程估计值趋于平缓并收敛到真实值，1 s最大误差控制在5 kg以内，相对误差为0.28%，因此误差精度完全符合质心侧偏角和轮胎侧向力的估计需求。在日常使用情况下，整车质量一定是在不断变化的，而整车质量作为估计模型输入，很大程度上影响了估计算法的准确性。车辆从停止到加速的行驶过程中，FFRLS算法会重新估计整车质量，并将新的估计值重新输入下一步的估计模块中，以提高估计的准确性。

质心侧偏角估计对比结果如图6所示，可见FFRLS与RCKF的联合估计对车辆质心侧偏角实现了准确的估计，达到了实时准确估计的需求；而RCKF算法由于质量未实时更新，最终估计会产生误差，尤其在估计曲线的波峰和波谷的位置；CKF算法设计没有考虑建模误差、未建模动态以及随机扰动等因素，失去了RCKF的鲁棒性，因此误差的偏差较大。在车辆这种复杂的非线性系统应用中，存在参数摄动、未知输入、系统过程噪声及测量噪声的影响，RCKF的基本原理是最小化最大估计误差协方差，从理论推导上证明可以提高对系统不确定参数摄动的适应性以及对未知输入和噪声的鲁棒性。

图6 质心侧偏角估计(高附着路面)

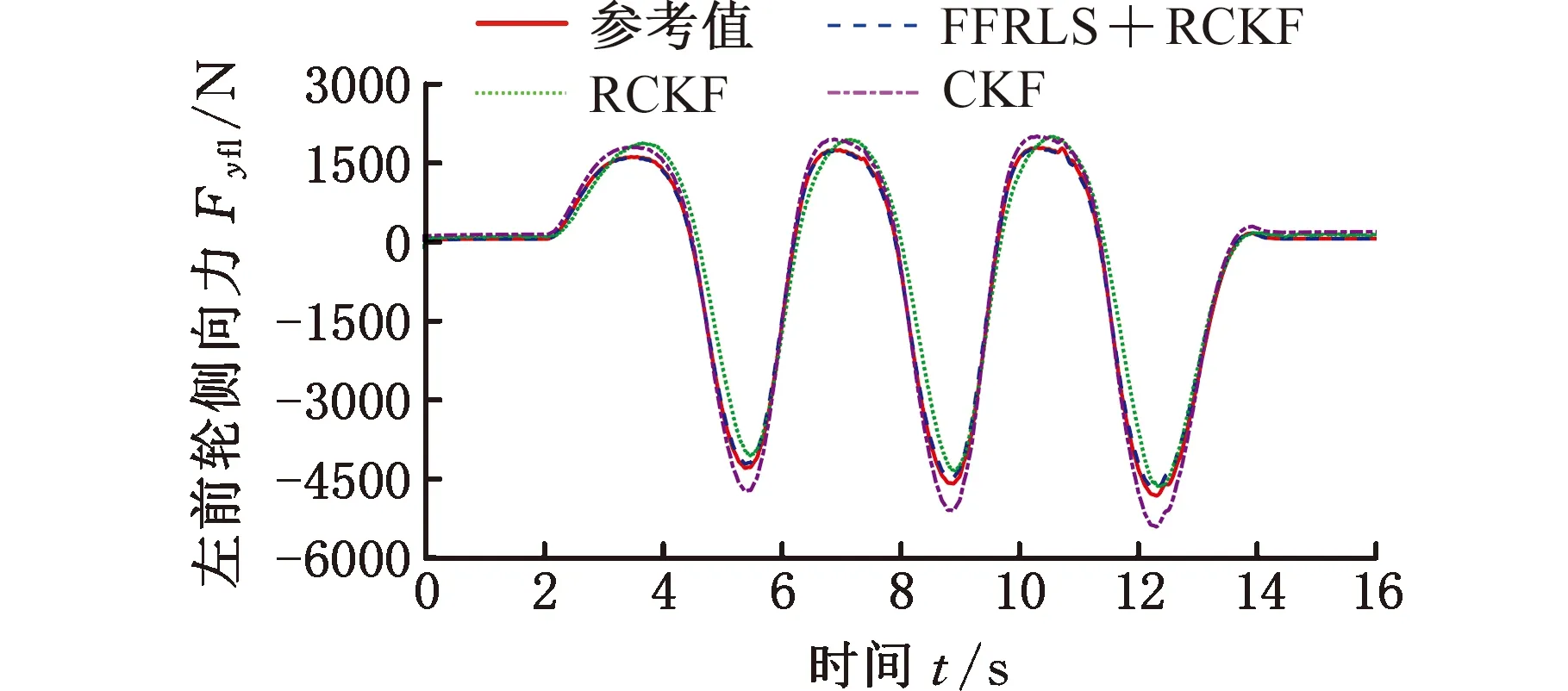
图7 左前轮侧向力估计(高附着路面)

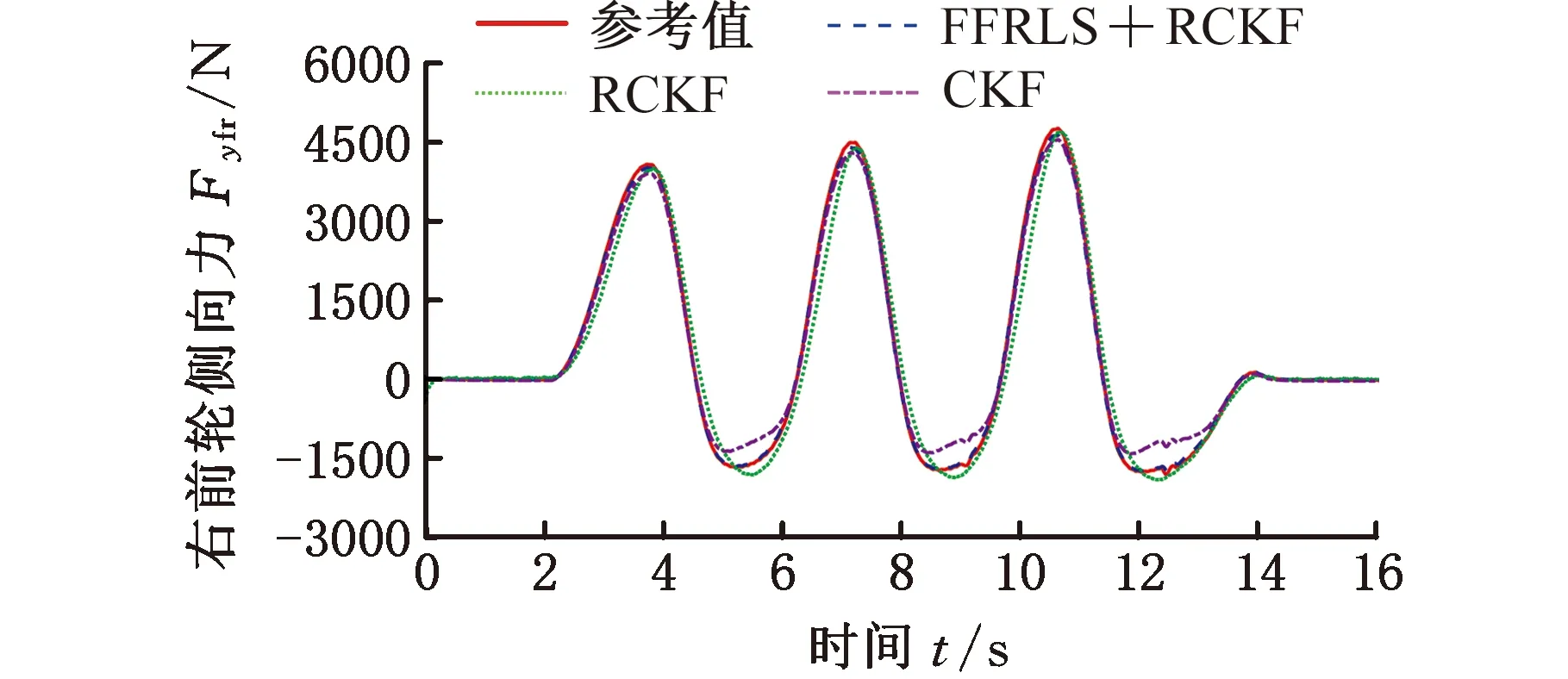
图8 右前轮侧向力估计(高附着路面)

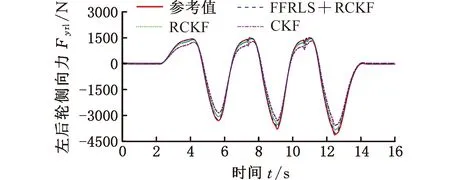
图9 左后轮侧向力估计(高附着路面)

轮胎侧向力的虚拟试验结果如图7～图10所示，基于FFRLS和RCKF联合估计的左前轮、右前轮、左后轮以及右后轮侧向力进行准确跟踪，达到了良好的估计精度，满足车辆运动控制和主动安全技术的需求；而RCKF和CKF的估计过程中都存在较大的偏差，尤其在估计曲线的波峰和波谷的位置，由于没有实时更新整车质量的输入、算法鲁棒性较差、车辆和轮胎未建模的动态特性等因素，当轮胎侧向力突然发生变化时，估计算法失去了很好的跟踪性能。由上述估计算法的对比结果可发现，此时建模参数的不精确、车辆系统未建模的动态特性均是导致最后估计结果偏差的因素，此偏差无法满足车辆运动控制和主动安全技术设计的需求，可见本文算法的优越性。

图10 右后轮侧向力估计(高附着路面)

为了进一步对比算法估计的准确性，本文采用平均绝对误差和均方根误差两项指标量化3种算法的估计结果，平均绝对误差可体现估计准确性，均方根误差可体现估计结果的收敛性和跟踪性能，对比结果见表2和表3。可以看出，基于FFRLS和RCKF的联合估计在估计精度和平稳程度上均有显著优势，能减小车辆系统未建模的动态特性、参数摄动、系统过程噪声以及测量噪声对估计的影响，有利于为车辆运动控制系统与主动安全系统提供更加可靠稳定的信息。

表2 估计值与真实值平均绝对误差(高附着路面)

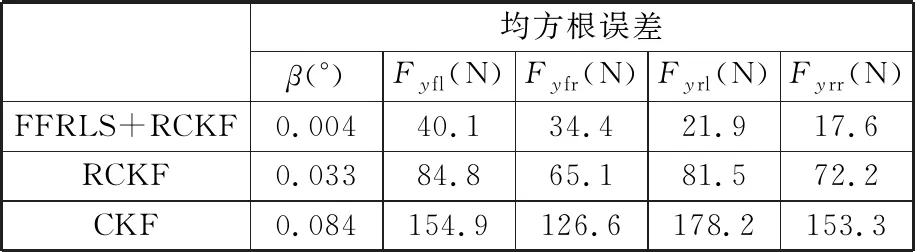
表3 估计值与真实值均方根误差(高附着路面)

4.2 低附着路面仿真试验与分析

仿真环境设置如下：在附着系数为0.3的路面上进行蛇形试验，其他参数设置和高附着路面工况相同，纵向和侧向加速度变化如图11所示。过程噪声协方差矩阵Q为I6×6，观测协方差R的值为0.1。

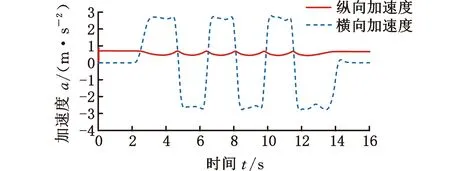
图11 纵向和横向加速度(低附着路面)

质量FFRLS估计算法中，整车质量估计初值为1000 kg，真实值为1800 kg，遗忘因子λ为0.97，FFRLS算法估计结果和真实值对比如图12所示。

图12 整车质量估计值与真实值(低附着路面)

当车辆行驶在附着系数较低的路面上时，由图12可见，在质量估计过程中，起始时刻曲线在真实值附近出现小幅波动，但波动范围不足以影响之后的估计算法模块的精度，在1 s内实现对真实值的较好跟踪，且后面的估计过程估计值趋于平缓并收敛到真实值，1 s最大误差控制在6 kg以内，相对误差为0.33%，因此,误差精度完全符合下一步估计的需求。

质心侧偏角估计对比结果如图13所示，可见FFRLS与RCKF的联合估计在低附着路面的工况下依旧对车辆质心侧偏角实现了准确估计，符合估计的要求；而RCKF算法在估计曲线的波峰和波谷的位置误差尤为明显；CKF算法相对于其他2种算法的估计偏差更大。

图13 质心侧偏角估计对比结果(低附着路面)

轮胎侧向力的虚拟试验结果如图14～图17所示，FFRLS和RCKF联合估计算法对四轮侧向力进行准确估计，达到了较为理想的估计效果；而RCKF和CKF的估计结果均存在较大的误差，估计算法失去了估计的准确性。

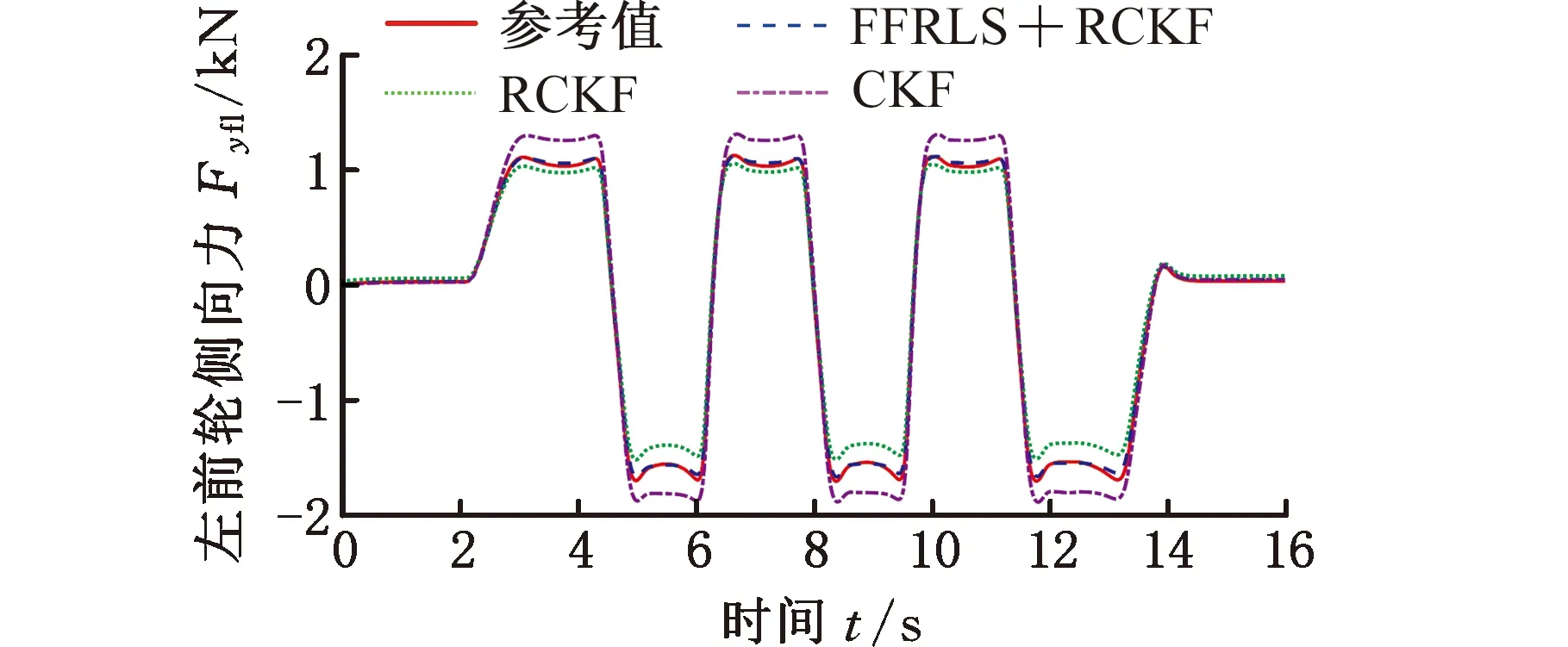
图14 左前轮侧向力估计(低附着路面)

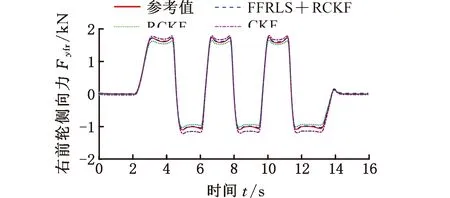
图15 右前轮侧向力估计(低附着路面)

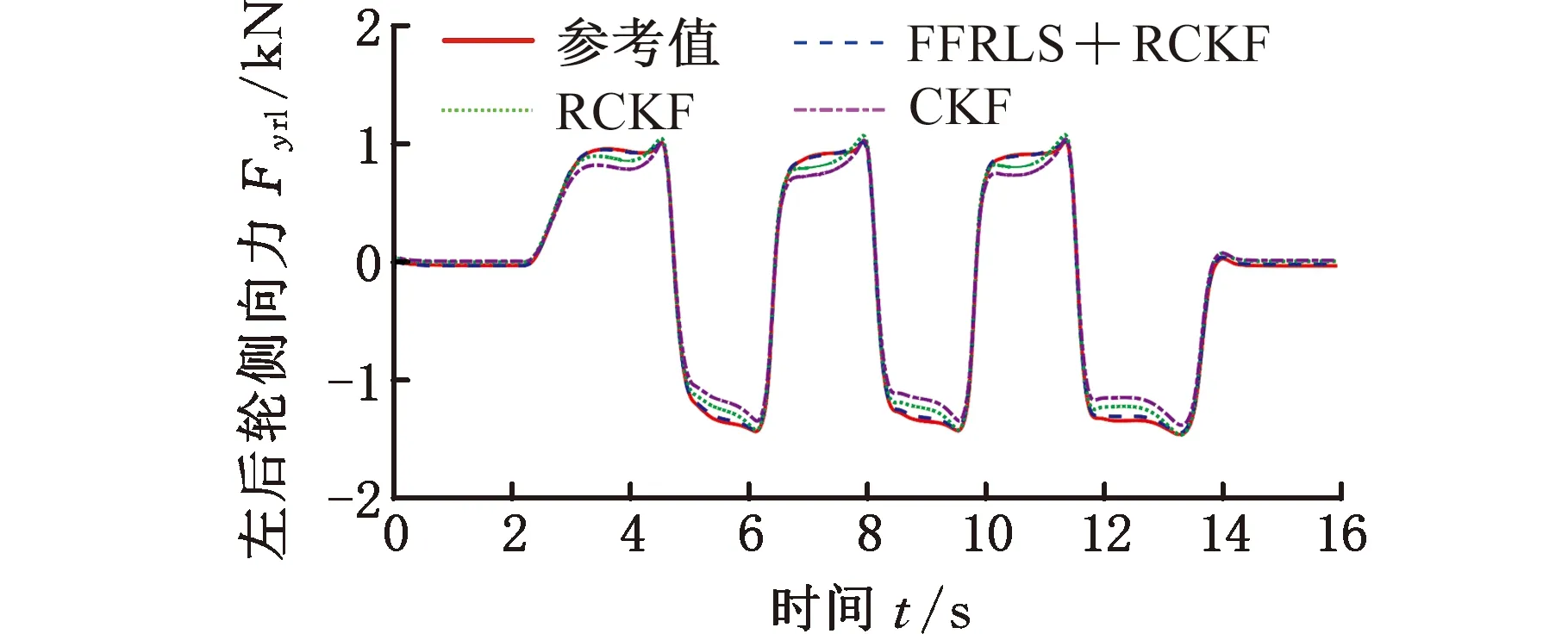
图16 左后轮侧向力估计(低附着路面)

图17 右后轮侧向力估计(低附着路面)

为了进一步对比算法估计的准确性，依旧通过上文的2项性能指标来体现估计准确性、收敛性和跟踪性，对比结果见表4和表5。可以看出，基于FFRLS和RCKF联合估计在估计精度和平稳程度上均有显著优势。

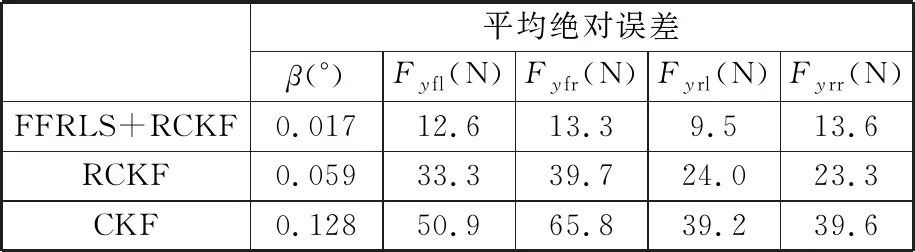
表4 估计值与真实值平均绝对误差(低附着路面)

表5 估计值与真实值均方根误差(低附着路面)

5 实车验证

为了验证本文算法，在已开发的四轮驱动乘用车平台上进行了实车试验，如图18所示。整车控制单元由ARM Cortex-M4内核的32位域控制器构成，同时配备了轮速传感器、转向盘转角传感器、GPS、惯性测量单元，便于获取所需的观测量。

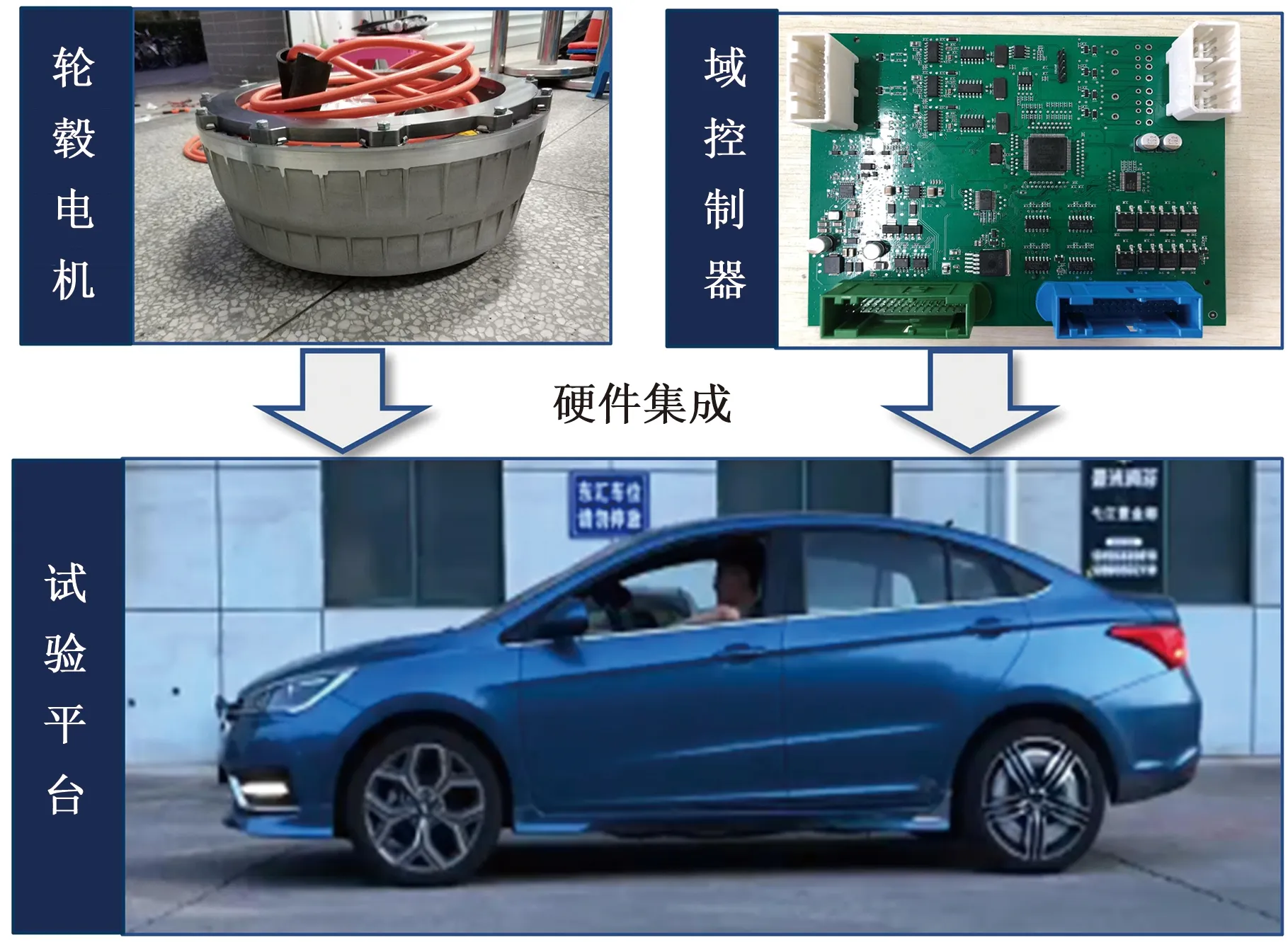
图18 实车试验平台硬件结构

本文实车试验由驾驶员驾驶车辆进行蛇形绕桩试验，前轮转角的变化如图19所示，初始车速为10 km/h，电机总转矩输入如图20所示，采样时间为0.01 s，纵向和侧向加速度变化如图21所示。过程噪声协方差矩阵Q为I6×6，观测协方差R的值为0.1。

图19 前轮转角输入(实车试验)

图20 电机转矩输入(实车试验)

图21 纵向和横向加速度(实车试验)

由图19可知，前轮转角的变化范围为-13°～12°。图20中由于本试验车辆设计了能量反馈制动的功能，出现了负转矩。由图21可知，纵向加速度在5 s、7 s、9 s、11 s、14 s、16 s左右出现较大的侧向加速度，而在9 s左右时侧向加速度达到0.47g，此时车辆进入非线性区。图22所示为FFRLS与RCKF联合估计方法对车辆质心侧偏角的估计结果与参考值的对比，可以看出，该方法实现了精准的估计，最大估计偏差在0.5°以内，质心侧偏角的偏差范围完全满足车辆运动控制和主动安全技术的研发要求。由图23可看到左前、右前、左后以及右后的轮胎侧向力估计结果，可见轮胎侧向力估计的趋势与范围，基本验证了轮胎侧向力的估计的准确性。

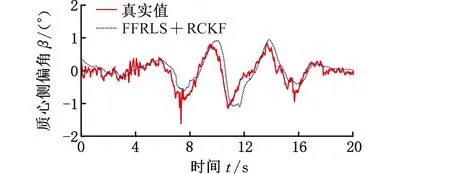
图22 质心侧偏角估计(实车试验)

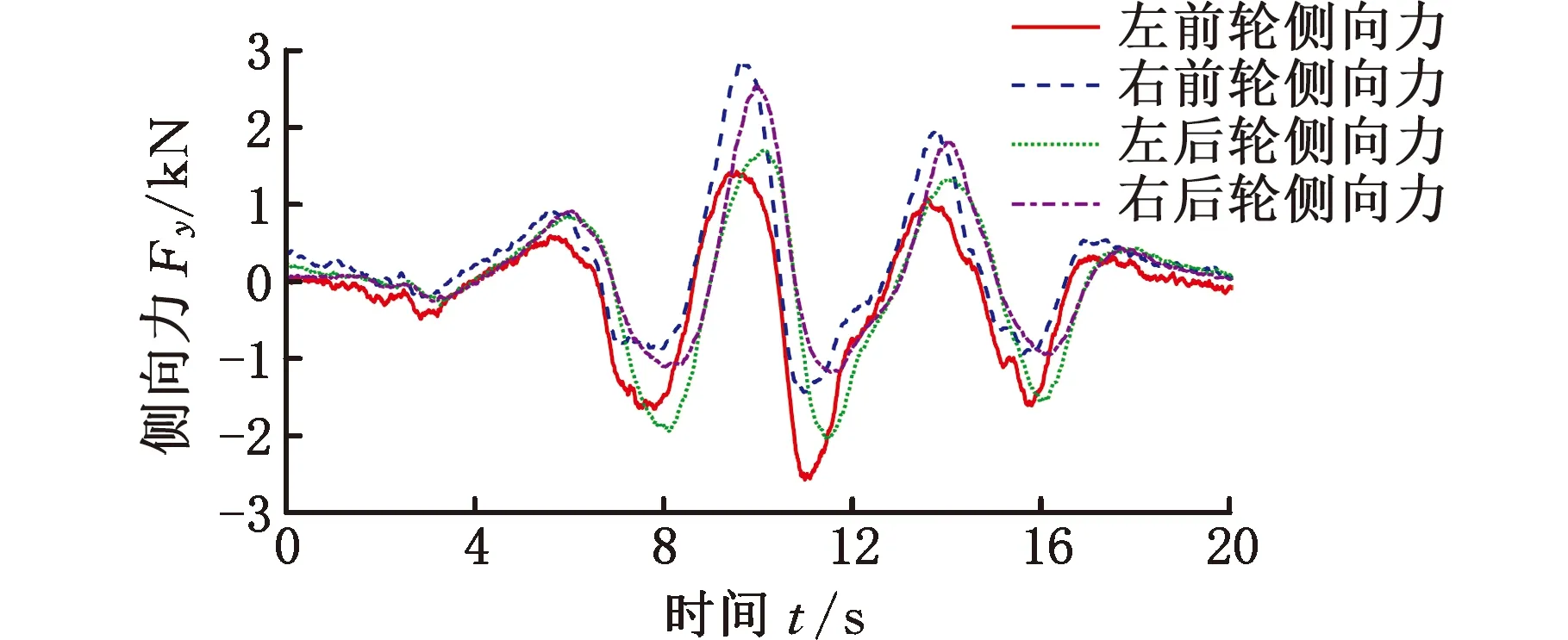
图23 轮胎侧向力估计(实车试验)

为了进一步量化算法的估计结果，选用平均绝对误差和均方根误差两项指标进行量化，见表6。可见平均绝对误差和均方根误差的数值在误差允许范围之内，由于无法避免传感器安装误差、实际情况中复杂环境激励对传感器测量的影响以及车辆结构振动等复杂因素，试验结果并没有与真实值完全贴合，后续研究将针对此问题作进一步改进。

表6 估计值和真实值的平均绝对误差与均方根误差(实车试验)

6 结论

(1)本文提出遗忘因子递归最小二乘法(FFRLS)与鲁棒容积卡尔曼滤波(RCKF)联合估计算法，以带有遗忘因子的递归最小二乘法实时估计整车质量作为新的输入，将极大值背景下的估计误差最小化嵌入标准容积卡尔曼滤波算法以实现鲁棒容积卡尔曼滤波，鲁棒容积卡尔曼滤波在Qk、Rk和P0未知的前提下，将Wk、Vk和X0的不确定性对估计结果精度的影响降到最低程度，提高了滤波算法的鲁棒性、准确性及抗干扰性。

(2)基于虚拟试验仿真验证了算法的准确性，在不同路面附着系数的不同工况下，试验结果表明，FFRLS和RCKF联合估计方法相对于参考值的误差小于RKCF、CKF滤波算法的误差。通过估计结果与真实值的平均绝对误差和均方根误差量化3种算法的估计准确性、收敛性和跟踪性，对比发现，FFRLS和RCKF联合估计的方法具有较好的优越性。

(3)基于自主研发的四轮驱动乘用车平台，搭载了ARM Cortex-M4内核的32位域控制器、轮速传感器、转向盘转角传感器、GPS、惯性测量单元，通过所观测的信息对质心侧偏角和轮胎侧向力进行了联合估计，验证了算法的准确性和鲁棒性。由此可见，所提联合算法具有较好的工程应用前景和价值，未来将进一步优化该算法，以节约车载控制器的计算资源。