圆柱齿轮滚切倒棱刀具设计

2022-11-25何晓虎杜彦斌

中国机械工程 2022年22期

何坤何晓虎杜彦斌

重庆工商大学制造装备机构设计与控制重庆市重点实验室，重庆，400067

0 引言

圆柱齿轮因其结构紧凑、承载能力强、传动比稳定，在高速重载场合广泛使用[1]。为了提高传动精度，延长使用寿命，倒棱是常用工艺手段，经过倒棱的圆柱齿轮可以避免因磕碰产生毛刺，同时可减小齿轮噪声[2]。目前采用的工艺类型主要有磨棱法和挤棱法[3]。磨棱法采用磨削方式进行倒棱，存在加工效率低、磨棱形状难以控制等问题；挤棱法采用挤棱刀与待加工齿轮做无侧隙啮合运动，对齿轮整个齿廓进行完整均匀地倒棱，但倒棱过程中会产生大量飞边，刀具设计也较为复杂。

随着对加工齿轮性能要求的日益提高，倒棱原理研究和倒棱刀具开发显得愈发重要。为此，国内外学者进行了大量的研究。韩伟娜等[4]基于半滚切法加工原理对螺旋锥齿轮副大轮齿顶线进行倒角加工研究，通过铣刀盘按照摆线进行间歇分度，从而对锥齿轮副大轮外锥面的内外齿顶线依次进行倒棱加工。李佳等[5]提出一种旋分倒棱加工方法，并验证了对螺旋锥齿轮齿顶倒棱加工的可行性。卞博等[6]提出基于锥形刀具的螺旋锥齿轮倒棱加工方法，提高了倒棱精度。WANG等[7]设计了锥形砂轮的倒棱结构，研究了砂轮结构尺寸和安装位置对锥面砂头结构的影响。HU等[8]介绍了一种双刃倒棱的机器人齿轮倒棱新方法，通过设计齿轮倒棱轨迹，同时对两个相邻轮齿的两侧进行倒棱。

目前螺旋锥齿轮的倒棱是研究热点，普遍采用盘形刀具间接分度逐一切削倒角进行倒棱加工，以螺旋锥齿轮为研究对象的倒棱刀具不适用于圆柱齿轮的倒棱加工[9-12]。国外已有公司将倒棱刀具与滚刀设计在同一主轴上，实现了滚齿工艺与倒棱工艺的复合，省去了专用倒棱机设备投入，但目前该技术对国内实行技术封锁，国内用户可定制专用倒棱刀具，但价格昂贵且定制周期长。为解决圆柱齿轮的高效齿廓倒棱需求，本文提出了滚切倒棱刀具前刀面廓形计算方法，为形成齿轮高效的“粗滚-倒棱-精滚”复合加工工艺提供理论基础。

1 滚切倒棱运动

1.1 倒棱参数及运动分析

区别于传统齿廓倒棱的磨棱法和挤棱法，本文研究刀具连续切削倒棱新方法。结合圆柱齿轮滚齿加工运动(图1)及端面齿廓倒棱需求，将刀具设计为单片多头的滚切倒棱刀具，刀具的齿数为滚刀的头数。刀具(随B轴转动)与齿轮(随C轴转动)通过连续滚切运动进行倒棱，利用刀具的前刀面刃形完成对齿轮端面廓形的倒棱。区别于齿面的滚齿展成包络原理，倒棱刀具廓形与齿轮倒棱目标廓形在每一个瞬时均为点接触，两个廓形不再是共轭齿廓，随着刀具与齿轮的连续滚切运动，左右齿廓的接触点非对称布置。

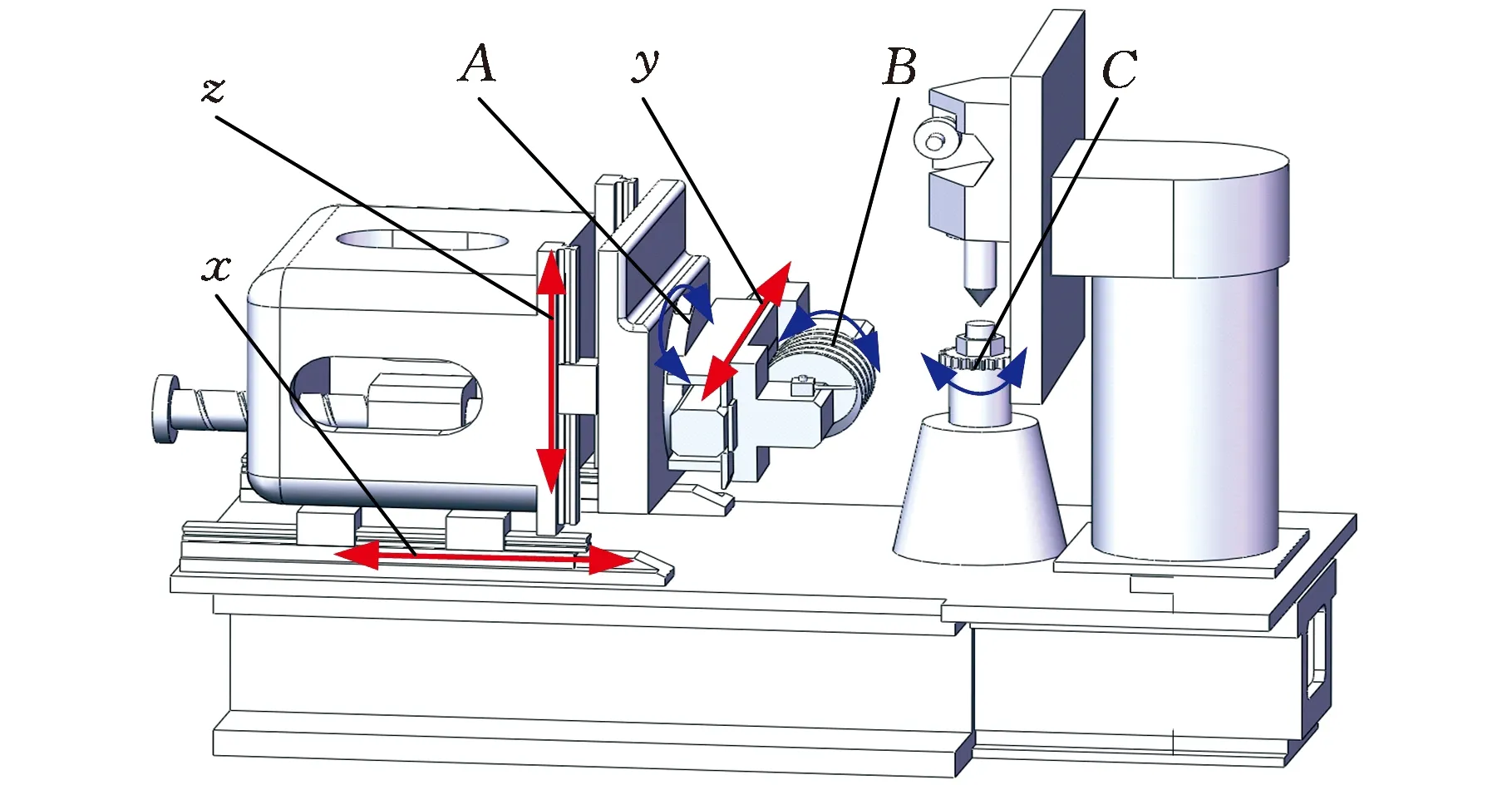
图1 圆柱齿轮滚齿运动

为避免刮伤齿面，利用图1中的x、y、z轴调整刀具的安装位置，利用A轴调整刀具的安装姿态。加工时刀具连续转动，齿轮连续分度，具有加工过程连续、精度高和效率高等优点[13]。

对倒棱效果的评价主要通过倒棱参数(倒棱厚度a、倒棱宽度b、倒棱角度c)来衡量(图2)，倒棱参数与齿轮的参数及刀具的安装参数密切相关。对于圆柱直齿轮，全齿廓倒棱角度一致，而圆柱斜齿轮则不同，因此，只在齿根圆处测量倒棱角度。在倒棱后的齿轮左右端面齿廓上对称选取一系列位置点作为倒棱效果评价点，通过对比倒棱效果评价点的倒棱参数大小，研究左右齿廓倒棱效果评价点的对称性及全齿廓倒棱效果评价点的一致性，分析滚切倒棱的效果。

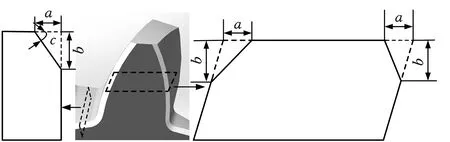
图2 倒棱参数

1.2 刀具安装位姿

齿廓倒棱不同于齿面加工，为避免在倒棱过程中刮伤齿面，需调整刀具的安装位置及安装姿态。刀具的初始安装位置参数包括中心高度h1、中心距p和初始倾角φs(图3)，其中，中心高度h1为刀具几何中心在z轴方向上与齿轮上端面的高度差，初始倾角φs与倒棱角度c互为余角，而在x轴方向上的中心距p与倒棱厚度a、倒棱角度c(初始倾角φs)及中心高度h1有关，即

图3 刀具初始安装位置

(1)

式中，hf为齿轮齿根圆直径。

根据刀具与圆柱齿轮的空间几何关系建立刀具安装位姿的坐标系(图4)，其中，刀具安装位姿包括安装姿态(安装角度β)和安装位置(安装高度h、中心距p、偏心距w)。建立参考坐标系omxmymzm和o1x1y1z1，均为静坐标系。其中，zm轴与齿轮轴线重合，原点在齿轮上端面圆心；z1轴与刀具轴线重合，原点在坐标系omxmymzm的omymzm平面上；o为刀具几何中心。

图4 刀具安装位姿坐标系

根据倒棱参数与建立的安装位姿坐标系，计算刀具安装位姿参数。以刀具螺旋升角确定刀具的安装角，刀具的螺旋升角与刀具参数相关，即

sinβL=mnzt/dt

(2)

其中，βL为刀具螺旋升角；mn为圆柱齿轮法面模数；zt为滚切倒棱刀具齿数；dt为刀具节圆直径。刀具安装角β为

β=βg±βL

(3)

其中，βg为齿轮螺旋角。安装角β与刀具及被加工齿轮的螺旋线方向及螺旋角有关，当倒棱刀与齿轮的螺旋线方向相同时，式(3)中取“-”号，相反时取“+”号。倒棱过程中，刀具前刀面与齿轮上端面初次无缝隙接触时的高度为刀具安装高度h(即刀具几何中心o点与齿轮静坐标系omxmym面的距离)，即

h=h1cosβsin(π/2-β)

(4)

刀具的偏心距w为刀具几何中心o点与齿轮静坐标系omymzm面的距离，即

w=h1cosβcos(π/2-β)

(5)

2 刀具前刀面廓形计算方法

滚切倒棱刀具的廓形与被加工齿轮端面廓形不再是共轭齿廓，因此，不能采用基于齿轮啮合原理的解析法求解刀具廓形。

2.1 端面齿廓

根据圆柱齿轮齿廓倒棱需求，完整倒棱齿廓包含2个部分：渐开线及齿根圆弧(图5所示，以左齿廓为例)。

图5 齿轮齿廓

(1)圆柱齿轮的左齿廓渐开线rL：

(6)

式中，α为展成角；rb为基圆半径；δ为初始偏转角。

(2)对于齿根圆弧，选定圆弧半径rc，根据起始展角as，确定圆心在渐开线起始点处，则左廓圆弧圆心坐标(xc，yc)为

(7)

在确定圆心坐标的基础上，建立左齿廓齿根圆弧的基本方程rcL：

(8)

由于齿轮端面齿廓的对称布置，故右齿廓的渐开线及齿根圆弧方程不再赘述。

2.2 空间运动坐标系

根据刀具安装位姿坐标系，建立刀具与齿轮的空间滚切运动坐标系(图6)。

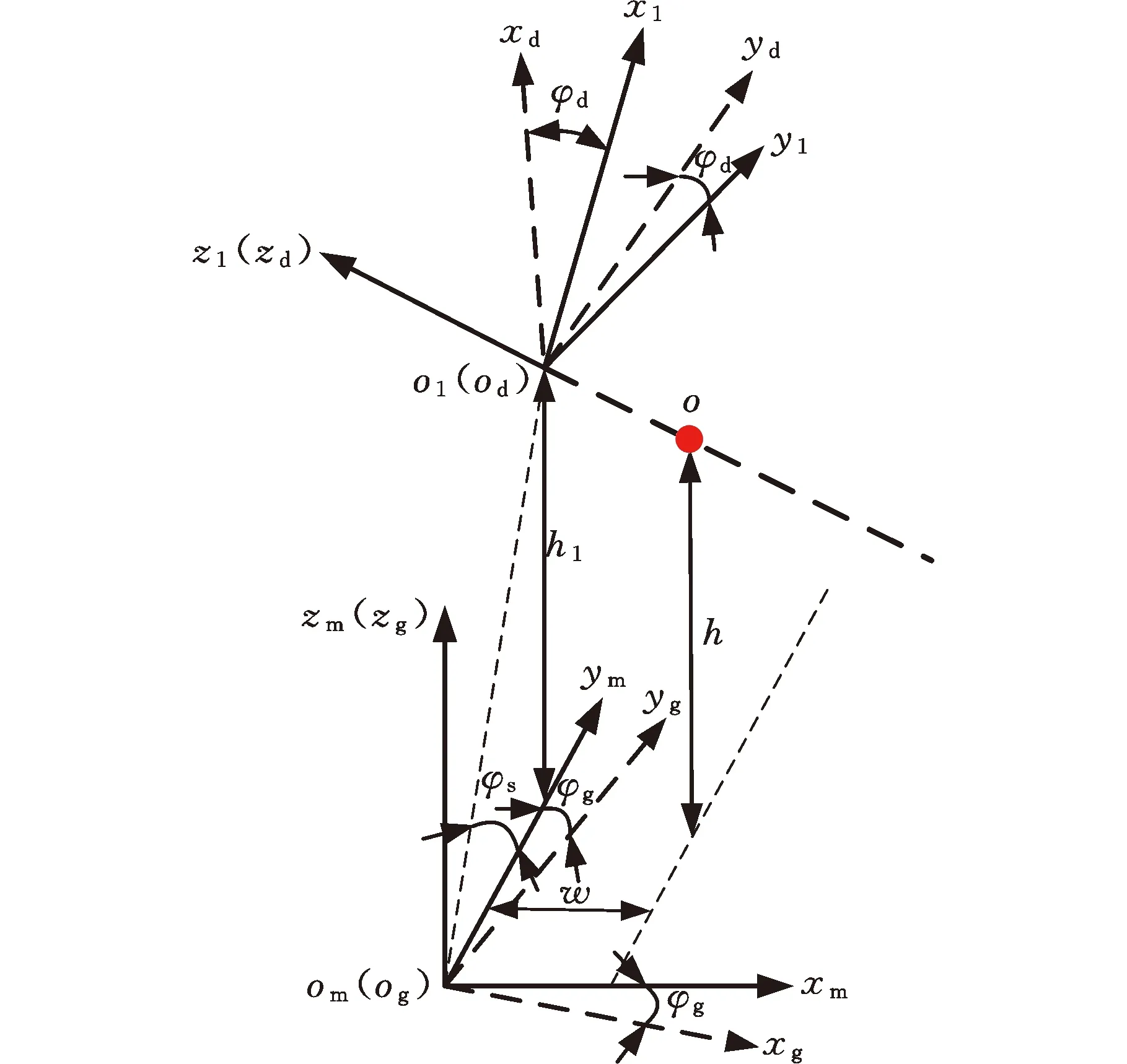
图6 刀具与齿轮的空间滚切运动坐标系

齿轮动坐标系ogxgygzg与齿轮固连，在初始位置与齿轮静坐标系重合；刀具动坐标系odxdydzd在初始位置与刀具静坐标系重合并与刀具固连。连续滚切倒棱过程中，齿轮绕zm轴顺时针转动角度φg，刀具绕z1轴顺时针转动角度φd。根据图6所示的刀具与齿轮的空间运动坐标系，推导各坐标系间的变换关系。齿轮动坐标系到齿轮静坐标系的坐标变换矩阵Mmg为

(9)

齿轮静坐标系到刀具静坐标系的坐标变换矩阵M1m为

(10)

刀具静坐标系到刀具动坐标系的坐标变换矩阵Md1为

(11)

其中，φs为刀具前刀刃与齿轮静坐标系omxmym面的夹角。有

φg=kφd/z

(12)

式中，k为刀具齿数；z为齿轮齿数。

由此可以将齿轮端面左齿廓渐开线廓形及齿根圆弧廓形表示在齿轮静坐标系omxmymzm中：

(13)

2.3 刀具廓形计算方法

连续齿廓倒棱过程中，齿轮绕C轴旋转，刀具绕B轴与齿轮滚动切削并且沿平行于z轴的方向轴向进给。距离齿轮端面廓形倒棱厚度的廓形是倒棱目标廓形，刀具的前刀面与倒棱目标廓形始终为点接触，且随着齿轮与刀具的连续滚切运动，左右齿廓的切削点非对称布置。求解滚切倒棱刀具廓形需要建立刀具与齿轮倒棱目标廓形的接触点示意图(图7)，图7表示齿轮端面左侧齿廓的刀具廓形的求解。

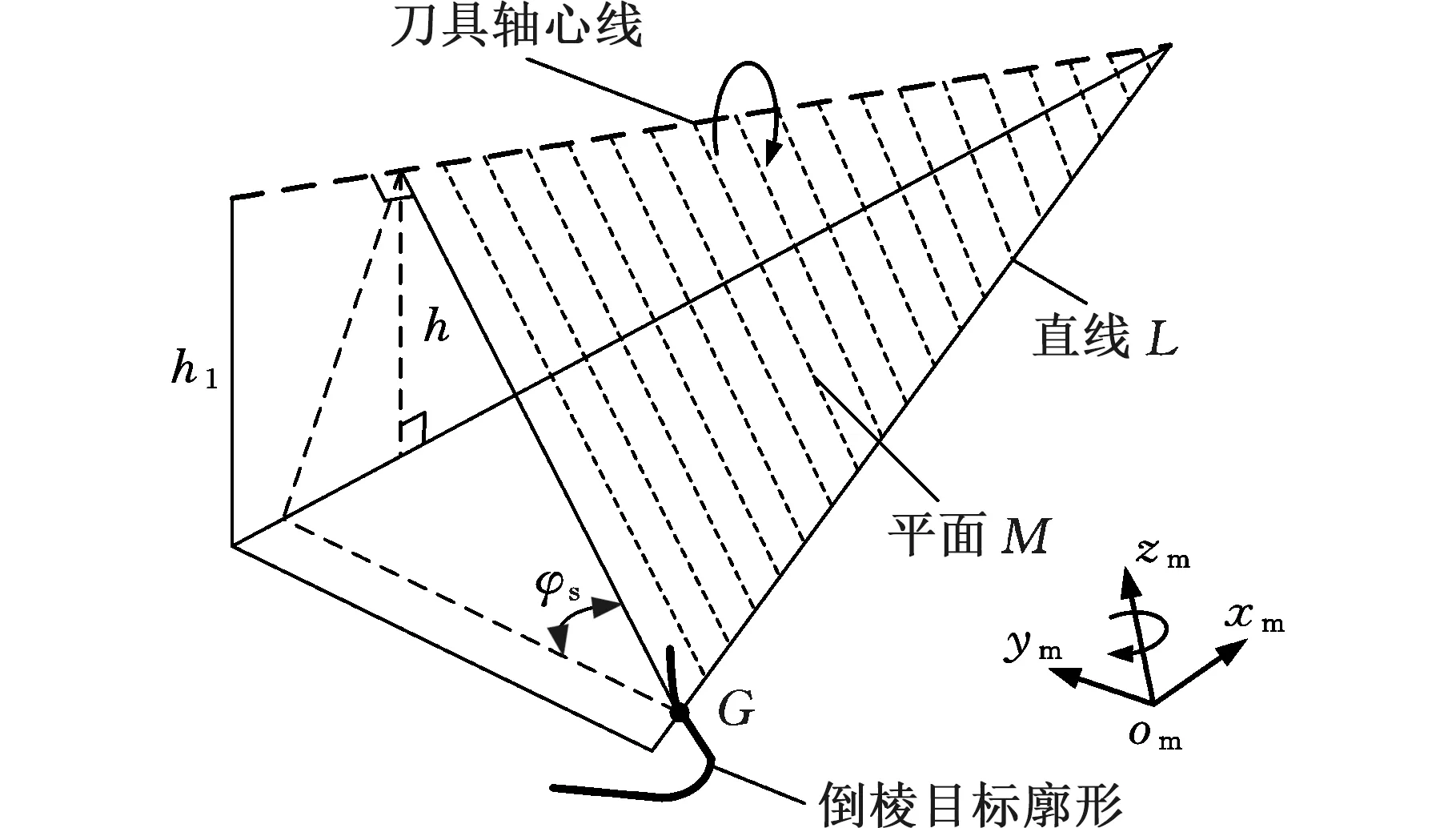
图7 刀具与齿轮的接触点示意图

过刀具轴心线作倾角φs的平面M，平面M为坐标系odxdydzd的xdodzd面，与坐标系omxmymzm的xmomym面相交于直线L,该直线L的方程为

ym=p-htan(φd+φs)

(14)

设直线L与倒棱目标廓形曲线相交于G点，G点为刀具前刀面与倒棱目标廓形的接触点，根据式(13)、式(14)将齿轮端面左齿廓形方程变化为倒棱目标廓形方程，随着刀具转动角度φd的变化分别与式(15)联立求解G点坐标：

(15)

将求得的G点坐标转换到倒棱刀具动坐标系中，得到刀具转动角度φd、齿轮转动角度φg位置处的倒棱刀具廓形点：

(16)

(17)

将齿轮继续旋转角度Δθ，刀具按滚切运动关系旋转角度Δη=zΔθ/k，得到对应齿轮转角φg+Δθ、刀具转角φd+Δη的接触点G′。按照统一步长重复进行计算，连续求解刀具前刀面与倒棱目标廓形的一系列接触点，圆滑连接各点，得到刀具左前刀面刃口曲线，完成刀具左廓形的计算。刀具右廓形坐标系间的变换及廓形点计算与左侧相同。

3 仿真及实验

3.1 切削仿真

选取圆柱斜齿轮(参数见表1)及滚切倒棱刀具(参数见表2)进行倒棱加工的切削仿真，验证刀具前刀面廓形计算及倒棱运动的正确性[14-17]。

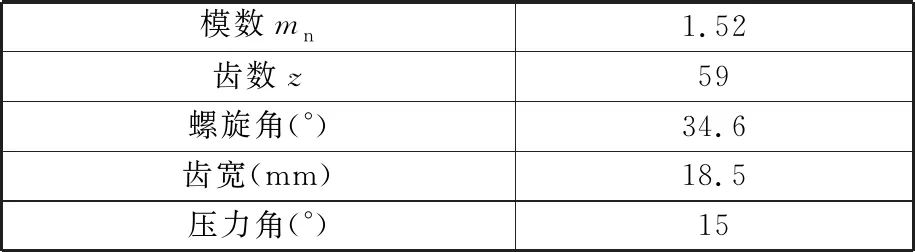
表1 齿轮参数

表2 刀具参数

初定滚切倒棱刀具齿数为4，在连续倒棱过程中，刀具的4齿相当于滚刀的4条螺旋线，刀具转一圈，齿轮绕自身轴线转过4个齿距，根据刀具与齿轮传动比，选择4齿可保证加工质量的均匀性，同时降低齿轮主轴转速。确定刀具的安装位姿(参数见表3)，其中安装高度、中心距、偏心距和安装角可由式(1)～式(5)分别计算得到。

表3 安装位姿参数

根据前述刀具前刀面廓形计算方法，基于MATLAB软件编写程序，计算刀具前刀面廓形，结果如图8所示。由于齿轮端面左右齿廓加工时有加工时间差且左右齿廓的接触点非对称布置，左右前刀面廓形不连续，故设计的刀具前刀面为了保证加工时无干涉，需将左右廓形圆滑连接，形成完整刀具廓形。

图8 刀具前刀面廓形

基于Solidworks完成齿轮及刀具的三维建模，按照刀具安装位姿参数配合，建立倒棱切削仿真模型(图9)，编写仿真运动程序，验证倒棱运动的正确性。

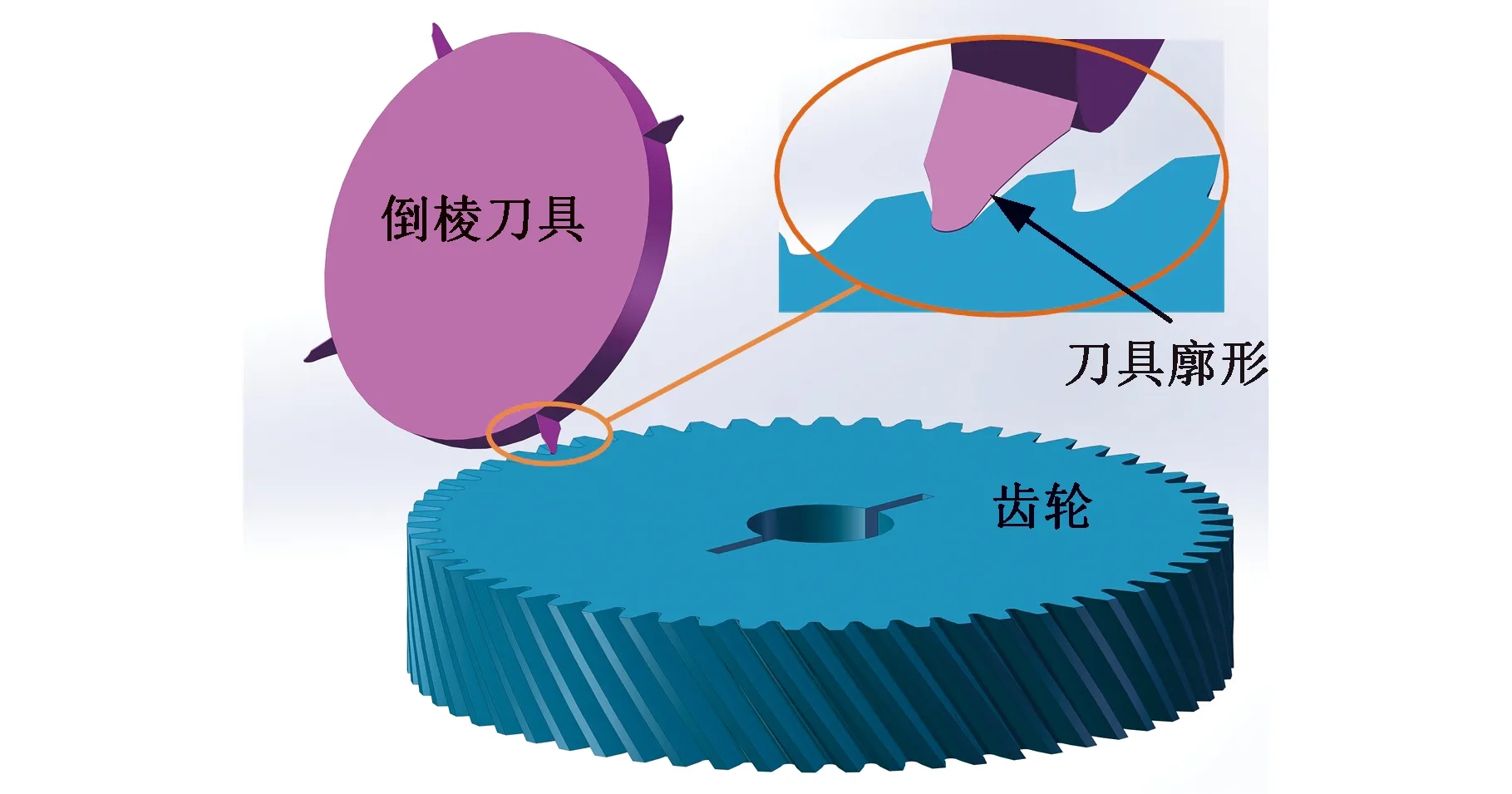
图9 倒棱切削仿真模型

倒棱切削仿真结果如图10所示，可以看出所设计的滚切倒棱刀具可以加工形成准确的齿廓倒棱形状。设置倒棱厚度为0.17 mm(误差允许范围0.01 mm内)，倒棱宽度为0.2 mm(误差允许范围0.01 mm内)，倒棱角度为50°(误差允许范围0.5°内)，在齿轮端面齿廓上选取一系列位置点作为倒棱效果评价点来分析滚切倒棱的效果。在除过渡圆弧的齿廓上选取8个位置点(图10中序号所示)，在齿槽左右齿廓的渐开线部分和齿根圆弧部分分别选取2个评价点，测量结果见表4。分析测量结果，全齿廓倒棱厚度、倒棱宽度的最大误差分别为0.0047 mm、0.0061 mm，齿根处倒棱角度最大误差为0.2°，结果均在误差允许范围内，说明全齿廓倒棱效果的一致性较好；左右齿廓对称位置处倒棱厚度、倒棱宽度的最大误差分别为0.0031 mm、0.0016 mm，齿根处倒棱角度最大误差为0.1°，结果均在误差允许范围内，说明左右齿廓倒棱效果的对称性较好。

图10 倒棱仿真结果

表4 倒棱测量结果

对比分析仿真结果的左右齿廓，由于齿轮的渐开线廓形与齿根廓形由过渡圆弧连接，过渡圆弧由于有较大的曲率变化，存在倒棱效果不均的现象(图11)，其中倒棱宽度差异较大，后续将进一步研究该局部区域的刀具廓形优化方法。

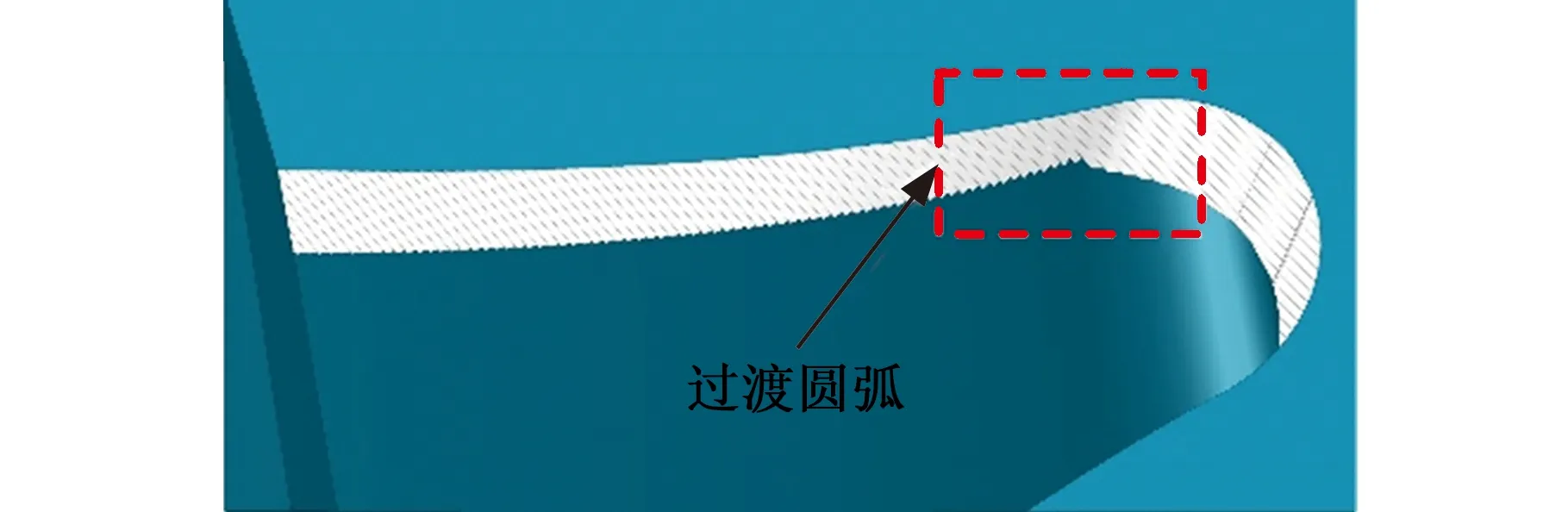
(a)右廓

3.2 实验验证

为进一步验证滚切倒棱刀具前刀面廓形设计方法的正确性和有效性，在某国产数控倒棱机上进行圆柱斜齿轮的滚切倒棱加工实验(图12)。

图12 倒棱加工机床

首先输入齿轮、滚切倒棱刀具和装夹的数据，将所设计的刀具安装至刀杆上；然后旋转A轴调整刀具安装姿态，调整后执行运动循环程序切削倒棱加工，齿轮绕C轴旋转，刀具绕B轴与齿轮滚动切削并且沿平行于z轴的方向轴向进给。倒棱加工实验结果如图13a、图13b所示；利用超景深三维显微系统对倒棱目标廓形进行观测和测量，如图13c、图13d所示，分别表示倒棱后的齿轮右廓及左廓，倒棱齿廓光滑平整，均匀无振痕，同时左右齿廓倒棱量除过渡圆弧处大小基本一致。与图10所示仿真结果对比分析，考虑加工及测量误差，实际测得的齿廓倒棱误差均在0.02 mm以内，验证了刀具前刀面廓形计算方法及倒棱仿真的有效性。