问题引领，促进深度学习

［摘  要］ 聚焦数学问题，以数学问题为引领，是激活学生数学思维、引发深度数学探究的有效方式. 文章以“椭圆及其标准方程”教学为例，探讨了基于问题引领的数学深度学习策略.

［关键词］ 问题引领；深度学习；椭圆及其标准方程

数学问题是数学活动的载体，也是激活学生数学思维、引发深度数学探究的有效方式［1］. 同时，聚焦问题的教学设计还可以引导学生明确数学思维方向，在问题的牵引下促使学生在问题探究和问题解决的过程中积累学习经验、获取相关的数学知识和技能.

“椭圆及其标准方程”是高中圆锥曲线的起始课，在教材安排上具有承前启后的作用. 一方面它是应用坐标法深化研究曲线的起点，另一方面为双曲线、抛物线的学习提供了理论基础和基本模式. 基于此，为了深入研究，文章结合学生的学习能力以及本节课程的重难点，通过问题引领的方式，让学生在开阔视野、问题解决中达到深度学习的目的.

问题的提炼与加工

要使“问题”在学习活动中能充分发挥引领作用，使学生在问题情境中引发深度思考、主动探究，首先应高度重视问题的提炼与加工，以及问题情境的创设［2］.

1. 创设问题情境，激发学生探究学习的兴趣

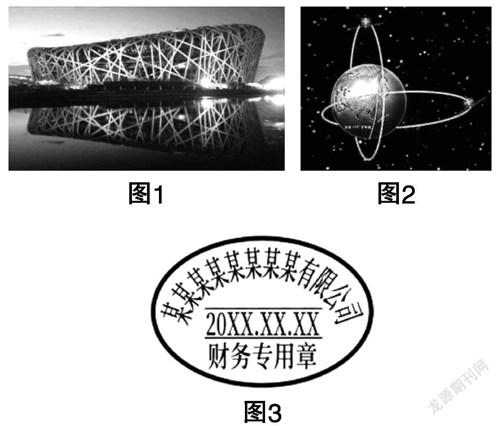
核心素养不是仅靠教师的讲授就能提高的，教师还应及时创设问题情境促使学生不断思考、感悟，从而让学生获得相关的学习体验. 基于深度学习，教师应特别重视教学情境的创设和问题的提出，可以结合学生的日常生活创设问题情境. 例如，“橢圆及其标准方程”教学中，教师应基于学生对日常生活的观察，利用鸟巢、天体运动轨迹、椭圆形公章等图形创设问题情境，引领学生在各种情境中发现和提出数学问题.

2. 创设驱动性问题，引领学生思维发展过程

驱动性问题能够促使学生主动探究、实践，因此教师还应在教学中创设一系列环环相扣的“问题串”，促使学生在“问题串”的引领下充分调动自己的思维，其中驱动数学实验的问题显得尤为重要. 例如，“椭圆及其标准方程”教学中，教师可以基于教学内容，应用笔尖描绘运动轨迹的数学实验，提出驱动性问题：如果笔尖到两图钉之间的距离之和等于细绳长度时，那么笔尖的运动轨迹是否是椭圆？如果实验中所用的细绳长度小于两图钉之间的距离，那么还能用笔尖描绘出相关的运动轨迹吗？等等.

3. 设计进阶性问题，促进深度学习

设计进阶性问题能够让学生的思维层层递进，能够让课堂充满激情，因此教师应设计进阶性问题，建立深度探究的意识，促使学生提炼解决问题的核心方式，形成探究事物规律的策略. 为了促使学生推导出椭圆的标准方程，教学中教师可以设计进阶性问题，由浅入深，层层递进，引导学生通过对问题的探究，认识和了解椭圆的标准方程，有效促进学生进行深度探究.

基于问题引领的高中数学深度学习策略

1. 情境导入，认识椭圆

数学知识并不是独立于社会环境而存在的，并且问题情境的创设不仅能够承载相关的学科知识，而且还能诱发学生的情感需求. 因此，在“椭圆及其标准方程”的教学实践中，为了激发学生的学习兴趣，先从感性上认识椭圆，教师可以结合学生的日常生活实际，及时呈现如下的实物和图片（如图1、图2、图3所示），最大限度地促使学生保持更为持久的学习动机.

2. 尝试探究，亲身体会

数学实验是数学活动中不可或缺的一部分，因此，为了培养学生的观察能力、归纳能力以及概括能力，促使学生通过动手画图或多媒体画图体验椭圆的形成过程，有效引导学生从感性认识向理性认识过渡，教师应及时呈现相关的实验设备，并通过问题引领的方式促使学生进行交流和思维碰幢.

例如，课前要求学生准备好细绳若干、图钉两枚、纸板一张，然后在课堂上进行实验操作. 首先要求学生将细绳进行对折，然后将细绳的两头用图钉固定在同一处，最后用铅笔将细绳绷紧进行旋转. 在此基础上，通过问题引领的方式及时引导学生进行深度思考.

问题1：在应用铅笔将细绳绷紧进行旋转的过程中，笔尖在纸板上绘制的运动轨迹是什么图形？

问题2：笔尖这个动点满足什么条件？能否用数学语言表述出来？

问题3：若将细绳的两头分别固定在不是同一地点的两处，然后用铅笔将细绳绷紧进行旋转，笔尖在纸板上绘制的运动轨迹是什么图形？

问题4：在问题3中，用铅笔将细绳绷紧进行旋转的过程中，哪些条件是不变的？

问题5：在问题3中，笔尖需要满足什么几何条件？能否用数学语言表述出来？

3. 归纳总结，完善定义

归纳总结有利于学生完善自己的知识结构. 因此，为了激发学生对新知的理解和认同，教师还应及时组织学生进行归纳总结. 在组织学生归纳总结椭圆的定义后，教师还应通过问题引领的方式引导学生理解和深化椭圆定义中的关键词汇，使学生能够真正理解椭圆的内涵和外延.

问题6：在问题3中，如果笔尖到两图钉之间的距离之和等于细绳长度，那么笔尖的运动轨迹是否还是椭圆？

问题7：在问题3中，如果细绳的长度小于两图钉之间的距离，会发生什么？

问题8：在问题3中，如果将两图钉之间的距离不断缩小，其他条件不变，那么椭圆的形状会发生哪些变化？如果将两图钉之间的距离不断扩大，其他条件不变，那么椭圆的形状又会发生哪些变化？

4. 合理建系，推导方程

推导方程是对现实问题进行数学抽象的过程，因此，为了让数学成为学生研究发现的动力，有效获得椭圆的标准方程，以及方程中每个参数的具体含义，教师还应通过问题引领的方式及时组织学生进行合理建系.

问题9：回顾求解圆的标准方程的一般步骤，思考当初是如何推导出以r为半径的圆的标准方程的.

问题10：类比圆的标准方程的推导过程，若要获得椭圆的标准方程我们应该如何建立坐标系？

问题13：引入参数b后，除了对称、简洁外，b还代表什么几何意义？

问题14：联系椭圆的标准方程的推导过程，试着判断出a，b的大小.

问题15：结合图4，在图中明确a，b，c的几何意义.

问题16：建立坐标系时，若焦点在y轴上，则椭圆的标准方程又是什么？

问题17：如何根据椭圆的标准方程判断其焦点的位置？

5. 初步应用，感悟新知

为了训练学生的语言表达能力以及思维的严谨性，加深对椭圆标准方程的记忆以及对a，b，c所代表的几何意义的理解，教师还应设置如下类似变式训练的题目，强化相关概念的理解.

问题18：请指出下列椭圆方程的焦点坐标以及相关标准方程中a，b，c的数值.

6. 小结归纳，巩固提高

小结归纳是深度学习不可缺少的环节. 因此，为了及时帮助学生将所学知识内化为自己的知识结构，教师还应及时通过问题引领的方式帮助学生进行归纳总结，让学生不断深化对椭圆方程的认知.

问题21：请用图示的形式归纳总结出本节课程的主要内容.

问题22：本节课程中蕴含了哪些数学思想？

总之，以问题为主线、以质疑为特征的问题引领教学更加注重学生“问题意识”的培养，能有效解决学生“从哪儿想”和“怎么想”的问题，提高学生发现问题、解决问题的能力. 因此，教师应最大限度地多角度创设问题，深层次地调动学生学习的动力，并在此基础上加强“教”与“学”的问题互动，从而达到打造深度课堂的目的.

参考文献：

［1］  姚璐. 深度学习背景下初中数学问题引领教学策略——以“因动点产生面积问题”的教学为例［J］. 中学数学，2021（06）：27-28.

［2］  郑毓信. 数学教学中的“问题引领”——中学视角下的“数学教学的关键”（3）［J］. 中国数学教育，2021（23）：3-6.

作者简介：毛妨妨（1990—），硕士研究生，中小学一级教师，从事高中数学教学工作.