核心素养导向下基于问题驱动的教学思考

［摘  要］ 结合“函数零点存在性定理”教学难点的突破，说明如何通过问题驱动，在合适的时机提出有梯度、有层次的问题，从而实现教学难点的突破，落实数学核心素养.

［关键词］ 问题驱动；函数零点存在性定理；数学核心素养

提出问题

数学概念、数学法则（公式、定理、公理等）是数学思维的细胞，是学习数学知识的基础.每个数学概念、定理、性质的产生和发展，对培养学生的思维、提升数学核心素养有着重要作用.数学教学是“过程”教学，因此挖掘概念、定理、性质的形成过程是数学课堂的教学难点.数学课堂的灵魂是思维，思维是通过问题来展现的，问题是思维活动的原动力和牵引力，在数学核心素养导向下，问题驱动就是一种有效的突破教学难点的教学模式.

“问题驱动式教学是指以‘问题’为载体，以学生为主体、教师为主导，学生自主探究与合作探究相结合，充分调动各方面的积极因素参与课堂教学，完成教学任务的教学方式.它有利于提升学生的数学核心素养，全面落实立德树人的根本任务.”［1］

笔者结合一次比赛课“函数零点”的教学片段，就课堂教学中如何创设问题，通过“问题链”驱动学生的思维“卷入”课堂，深入理解教学难点，与大家交流.

课堂教学实录

1. 提出问题——引入定理，展示定理的形成背景，找准数学核心素养的切入点

介绍完函数零点的定义以及求解简单函数的零点后，教师提出问题：函数f（x）=x5+x－6有零点吗？若有，请求出零点. （学生立马拿出计算器，但由于要解的是高次方程x5+x－6=0，学生发现计算器无法求解五次及以上的方程.）

设计意图：一个看似非常简单的函数零点问题却不能用计算器求解，激发了学生的好奇心和求知欲.

师：能不能用其他的方法先判断它有没有零点呢？函数的零点除了与对应方程的根等价，还与对应函数的图像与x轴交点的横坐标等价，当我们无法进行方程求根时，我们能不能作出对应函数的图像呢？（停顿几秒）

设计意图：巩固前面的新知：函数的零点可以从数形两个角度进行探究.数不行，就从形入手，考查学生利用函数的性质作出函数大致图像的能力，渗透数形结合思想，培育学生逻辑思维核心素养.

师：对于一个陌生的函数，我们可以用什么方法作出其大致图像呢？

众生：描点法.

师：非常好，那就开始吧. （教师在学生之间巡视）

生1：我发现有零点！

师：怎么发现的？

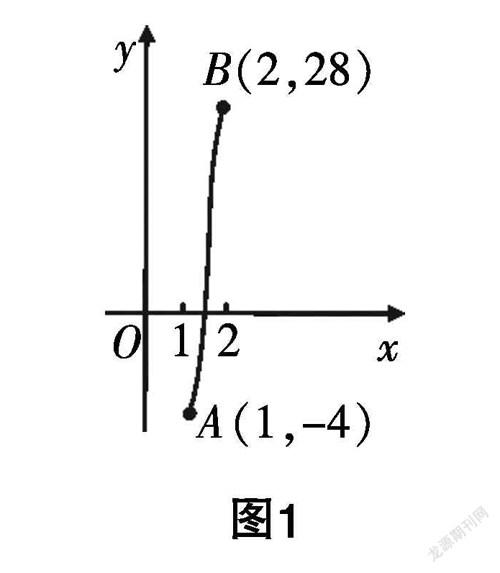
生1（带着自信的表情）：取三个点（0，-6），（1，-4），（2，28），用光滑的曲线连起来，图像与x轴相交，说明该函数有零点. （由于大多数学生取的也都是这三个特殊点，因而赞成该结论.）

师：那你怎么知道这三个点之间的曲线走势一定是这样的呢？

设计意图：培养学生严谨的数学理性精神，也是对过去所学知识、经验的考查，同时培养学生直观想象、数据分析等核心素养.

生2：因为f（x）是单调递增的，所以曲线一定是光滑向上的. （底下传来一阵掌声）

师：非常棒！生2结合我们上一章学习的函数的性质画图，体现了用数学思维解决问题的能力.那大家知道该零点存在于哪个区间吗？

众生：（1，2）.

2. 提出难点——形成定理，探究定理背后的本质，挖掘数学核心素养的生长点

师：很好，我们能否探究出到底是什么原因导致该函数在区间（1，2）内必存在零点呢？

设计意图：通过不停追问，抽丝剥茧，揭示教学难点背后的本质属性.

生2：因为它的值域是R，所以一定存在x使得f（x）=0.

師：你能解释一下它的值域为什么是R吗？

生2：因为y=x5，y=x是奇函数，值域都是R，相加所得函数的值域还是R.

师：生2发现该函数一定存在零点，非常不容易了，但为什么零点一定在区间（1，2）内，还是没有给出理由，大家继续思考原因到底是什么. （给予学生充分的时间思考）

设计意图：教师的追问与学生的思维碰撞，追根溯源，探究定理的本质，培育学生逻辑推理核心素养.

生3：因为（1，-4），（2，28）这两点“一上一下”，所以曲线一定会穿过x轴，因此零点一定在区间（1，2）内. （其他学生恍然大悟，频频点头.）

3. 突破难点——获得定理，经历定理的形成过程，紧扣数学核心素养的着力点

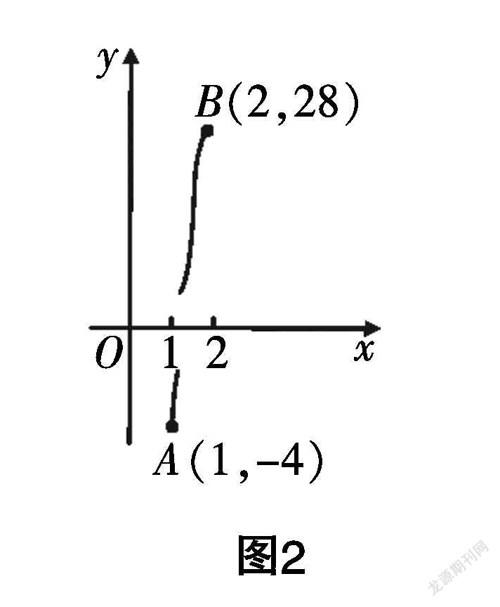
师（继续追问）：有两个点“一上一下”，连接该两点的曲线一定会穿过x轴吗？（教师画出如图2所示的图像）

众生：哦，还必须满足这个函数的图像是连续的.

师：对！只有函数的图像连续不断，当两点“一上一下”时，函数的图像必然会穿过x轴.这里的两点“一上一下”，同学们能否转化为数学符号来表示？

设计意图：将图形语言转化为数学符号语言，培育学生数学抽象、直观想象、数据分析等核心素养.

生4：坐标系中点的上下即代表函数值的正负：f（1）<0，f（2）>0.

师：很好，那大家能否归纳总结出一个函数在某区间内存在零点的充分条件？

生5：在某区间的端点值异号，曲线连续.

师（板书）：若y=f（x）在［a，b］内连续不断，当f（a）f（b）<0时，y=f（x）在（a，b）内存在______个零点（故意留白）.

师（追问）：请问在这个区间内有几个零点？一定是一个吗？

设计意图：由特殊到一般，形成定理. 培育学生数学抽象、直观想象等核心素养，体会数形结合思想.

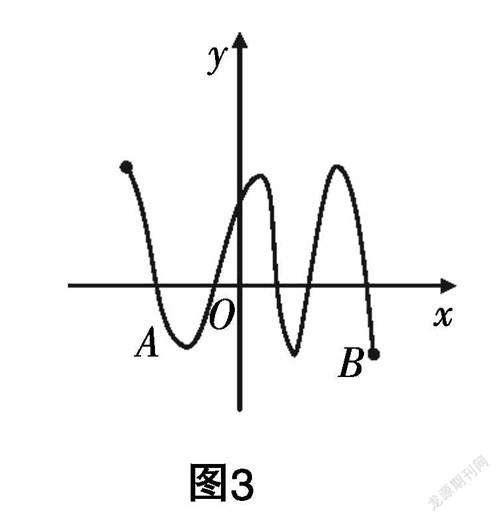
众生：可以是多个（单调就一个，不单调就多个）.

师：谁上黑板画出多个零点的情形？

生6作图如下（如图3所示）：

教师补充板书：至少存在一个零点.

师（用PPT展示）：若函数y=f（x）在区间［a，b］上的图像是一条连续不断的曲线，并且满足f（a）f（b）<0，则函数y=f（x）在区间（a，b）内至少有一个零点. 这就是今天我们学习的函数零点存在性定理.

4. 理解难点——定理的升华，达成定理的全面认知，夯实数学核心素养的落脚点

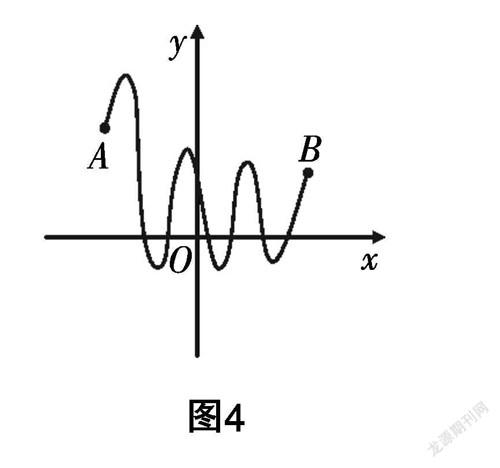
师：已知函数y=f（x）在区间［a，b］上的图像是一条连续不断的曲线，如果f（a）f（b）>0，函数y=f（x）在区间（a，b）内就一定没有零点吗？

设计意图：深入理解函数零点存在性定理的内涵与外延，掌握该定理的本质，在师生交流、反馈中完善对该定理的认知，培养学生逻辑推理、直观想象等核心素养.

生7：不一定，可能有，也可能没有.

师：你能作图举例说明吗？

生7上黑板作图（如图4所示）：

师：零点存在性定理是函数存在零点的什么条件呢？

众生：充分非必要条件.

（以下教学过程略）

案例反思

本节课的最大亮点是问题驱动教学模式，教师以一个又一个环环相扣的问题为载体，引发学生对问题进行思考、探究，达到“以问引思、以问促动”的教学效果，进而突破难点. 问题驱动教学模式的关键及核心是“问题”，问题设计得恰到好处，收到的效果往往也会出乎意料. 在本节课中，教师设计的问题具有以下三大亮点：

1. 提出的问题符合学生的最近发展区

选择一个恰当的问题，创设一个好的问题背景，调动学生共同参与课堂教学是提高课堂探究活动有效性的关键所在. 在本节课中，教师始终围绕与函数f（x）=x5+x－6的零点相关的问题展开教学，从该函数是否有零点，到零点存在于哪个区间，以及为什么存在于该区间，师生共同经历了这一系列问题的解决过程，最终实现了教学难点的突破和教学目标的达成.

教师之所以选取函数f（x）=x5+x－6的零点问题贯穿教学始终，是因为该函数对应方程的根只用计算器求解是无法得到的，使得它的零点存在性问题的解决具有挑战性，能激发学生的好奇心，给学生带来认知冲突. 另外，高一学生的知识储备中已有基本初等函数的简单性质，利用描点法及该函数的单调性可大致作出其图像，从而找到解决难点的突破口；在定理的形成过程中，利用该函数的性质去解决问题，这些都是学生“跳一跳”就可以够得着的，符合学生在最近发展区提出问题的原理. “学生在活动中发现，在合作中增知，在‘教’与‘学’中互促互动，这对启迪学生思维、发展数学核心素养大有裨益.”［2］

2. 提出的问题具有层次性

问题是数学的心脏，问题的层次性和递进性是促进课堂探索活动深入展开的动力. 在本节课中，教师为了突破教学难点，精心设计了一系列层次分明的问题，由简单到复杂，激发了学生的学习兴趣，达到了教学难点逐步渗透、逐层深化、螺旋上升的教学效果. 从一开始的“f（x）=x5+x－6有零点吗？”到“若有，零点存在于哪个区间？”到“什么原因导致零点存在于该区间呢？”到“两点的‘一上一下’能否转化为数学符号语言呢？”再到“如果函数在某区间的端点值异号且图像连续，那么函数在该区间内有几个零点？”通过问题的层次性和递进性突破难点、获得定理.

这一系列问题的设计坡度适宜、步步相因、环环相扣、层层相递，一步一个台阶把问题引向深入. 解决问题的同时学生的思维也得到了锤炼，学生在问题解决中学习，在学习中产生新问题，通过问题的解决培育学生数学抽象、逻辑推理、直观想象、数据分析等数学核心素养.

3. 提出的问题具有合适的时机性

问题驱动式教学的关键就是“提问”，而提问的时机是有效提问的保证. 在本节课中，介绍完函数零点的定义以及求解简单函数的零点后，学生轻轻松松地解决了相应问题，很有成就感，教师此时立马提出了新问题：“函数f（x）=x5+x－6有零点吗？”难度上升，直击难点，问得及时且具有挑战性，激发了学生的求知欲. 在获得零点存在性定理后，教师并没有让学生的思维停滞下来，而是趁热打铁又抛出了新的问题：“函数y=f（x）在区间［a，b］上的图像是连续的，如果f（a）f（b）>0，就一定没有零点吗？”教师在学生刚获得定理、思维处于兴奋状态时抛出了新问题，及时捕捉到了提问的时机，启发学生继续思考，促进学生对定理认知的升华. 既体现了学生学习的主体地位，又真正发展了学生的数学核心素养.

“高中数学教学以发展学生数学学科核心素养为导向，创设合适的教学情境，启发学生思考，引导学生把握数学内容的本质.”［3］核心素养导向下的问题驱动式教学，调动了学生学习的能动性，提升了自主学习能力，这就要求一线教师深入教学实践，思考如何结合学情设计难度适宜、层次清晰、时机恰当的问题，通过“问什么，怎么问，何时问”把学生的思维“卷入”课堂，通过润物无声的渗透，在课堂实践中培育学生的数学核心素养，在课堂实践中落实数学核心素养.

参考文献：

［1］  侯有岐. 基于核心素养的高中数学问题驱动式教学实践研究［J］. 数学教学研究，2020（02）：2-6.

［2］  严丽香. 以问题驱动探究 促核心素养提升——以“指数函数及其性质”教学为例［J］. 数学教学研究，2020（03）：30-33.

［3］  中华人民共和国教育部. 普通高中数学课程标准（2017年版）［M］. 北京：人民教育出版社，2018.

作者简介：吴其明（1990—），硕士研究生，中学一级教师，从事高中数学教育教学工作，曾获上海松江区课堂教學评比一等奖.