新旧版高中数学教材对比分析
2022-11-23何业亮贺小雪
何业亮 贺小雪

[摘 要] 函数贯穿了整个高中数学学习,它具有基础性、工具性、启发性,为学生提供了解题思路,推动了解题流程,函数在高中数学学习中有着不可估量的作用.新旧版高中数学教材对函数的部分定义也发生了改变,下面以“两个函数相等”的定义为例对比分析新旧版教材的差异.
[关键词] 高中数学;新旧版教材;函数定义
对旧版教材定义的分析
人教A版高中数学必修1教材将“两个函数相等”定义为(以下记为“旧版教材定义”):如果两个函数的定义域和对应关系完全一致,我们就称这两个函数相等[1]. 由上述定义可知,若两个函数存在相等关系,那么必须满足的条件有两个,一是定义域相等,二是对应关系相同.
文[2]提出了疑惑:如果两个函数只存在定义域相等,但对应关系不同,那么这两个函数是相等的吗?然后举了两个例子(见例1和例2),得出“有可能相等”的结论,最后指出“‘旧版教材定义’的表述存在歧义”.
例1 已知函数f(x)=x+1与g(x)=x2+1的定义域都是{0,1},判断这两个函数是否相等.
例2 已知函数f(x)=x与g(x)=x4的定义域都是{-1,0,1},判断这两个函数是否相等.
文[3]指出上面例1中的两个函数的对应关系是相同的,然后分析大学阶段“关系说”的函数定义,最后草率地肯定“旧版教材定义”.
1. 疑惑
(1)两例中的两个函数的对应关系是否均相同?
解决这个问题的关键是准确理解函数的对应关系.据笔者调查,将其理解为施加在自变量上的运算关系非常流行. 譬如,函数g(x)=x2+1的对应关系是自变量的平方再加1. 事实上,这种体现对应过程的理解是肤浅的、片面的. 笔者认为,函数的对应关系反映的是对应的结果,如果两个函数的对应关系相同,那么它的本质是对自变量的同一个取值,都会有相同的函数值与之对应. 文[2]和文[3]都未说清这一点,均停留在“对应过程”层面. 由于例1中的对应关系(x→y)是0→1,1→2,例2的对应关系(x→y)是-1→1,0→0,1→1,故这两例中的两个函数的对应关系均相同,只是对应过程的“表现形式”(即解析式)不同而已.
(2)“旧版教材定义”是否有问题?
笔者查阅苏教版、北师大版和人教B版高中数学教材,发现都未提及“两个函数相等”的定义. 但仔细品读这三个版本的高中数学教材会发现:这四个版本(含人教A版)教材对函数概念的叙述基本相同,都是源自法国布尔巴基学派所完善的函数“关系说”定义,只不过是简化型和浓缩版. 不难看出,构成函数的要素是定义域、对应关系和值域. 而函数的值域又是由函数的定义域和对应关系所决定的,故“旧版教材定义”没有根本上的问题. 文[2]提到了一个大学版“两个函数相等”的定义(以下记为“大学版定义”):若两个函数f与g有相同的定义域D,且对每个x∈D,两个函数的函数值f(x)与g(x)相等,则称两个函数相等. 笔者认为它与“旧版教材定义”的本质相同,但各有千秋.具体来讲,“旧版教材定义”较精炼,便于学生记忆;“大学版定义”虽然翻译了两个函数的对应关系相等,但操作性稍逊色.实证表明,在非定义域的范围内或忽略定义域去判断两个函数的对应关系是否相等是普遍现象,极不严谨,有时会出错,但不能把原因归为“旧版教材定义”有问题. 故在此基础上,新版教材对旧版教材的“两个函数相等”的定义做了补充和修改.
新版教材对定义的完善
人教A版高中数学必修第一册教材对“两个函数相等”是这样定义的(以下记为“新版教材定义”):如果两个函数的定义域相同,并且对应关系完全一致,即相同的自变量对应的函数值也相同,那么这两个函数是同一个函数. 由此我们亦可得,两个函数相等的必需条件是:第一,定义域相等;第二,对应关系相同;第三,相同自变量对应的函数值相同. 相对于旧版教材,新版教材在原定义的基础上增加了“相同自变量对应的函数值相同”.
例3 已知函数f(x)=1与g(x)=sin2x+cos2x的定义域都是R,判断这两个函数是否相等.
例4 已知函数f(x)=x+1与g(x)=x2+1的定义域都是(0,1),判断这两个函数是否相等.
函数中的对应关系是指“输入值集合中的每项元素皆能对应唯一一项输出值集合中的元素”,因此对应关系相等,应该是两个函数取同一自变量时,对应的函数值相同. 例3中的两个函数,当x取任意值时,f(x)与g(x)都是相等的,且都等于1,两个函数的定义域相同,对应关系相同,相同的自变量对应的函数值也相同,因此f(x)=1与g(x)=sin2x+cos2x是相等的函数.例4中的两个函数,当f(x)在定义域范围内取x=0.5时,f(0.5)=1.5;当g(x)在定义域范围内取x=0.5时,g(0.5)=1.25,因此f(0.5)≠g(0.5). 可见这两个函数的定义域相同,值域相同,但对应关系不同,因此它们不是相等的函数.
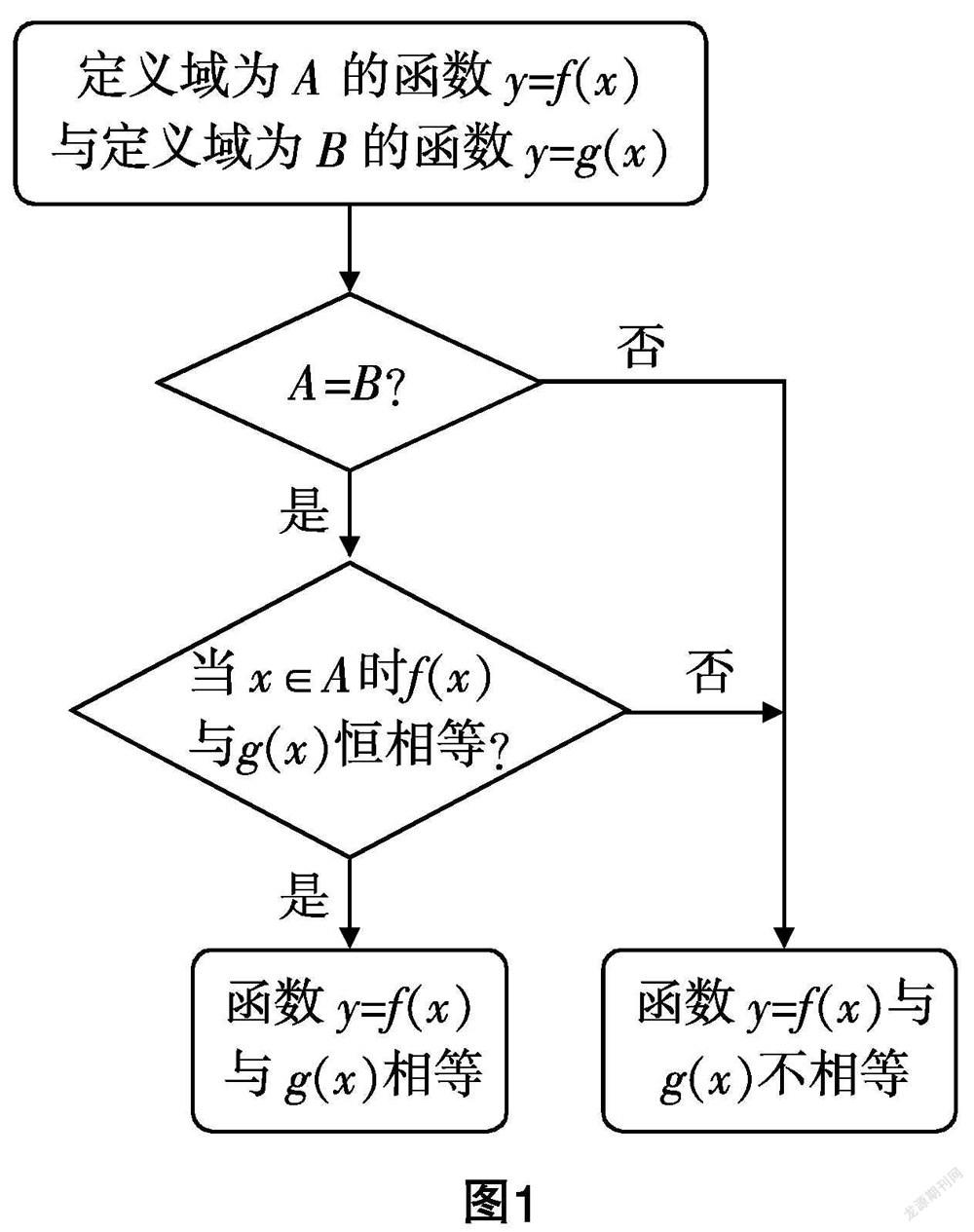
新版教材在旧版教材的基础上加了一个条件,即相同的自变量对应的函数值相同,使原来的定义更加完善. 为了严谨起见,下面给出了用定义判断两个函数是否相等的操作流程(见图1).
总结和建议
1. 敬重教材
教材是许多数学工作者的心血,他们经过斟酌敲打,最后才有智慧结晶. 所以应敬重教材,要学会高瞻远瞩地品读教材.
从句子品读,体会微言大义.不仅更能揭示函数概念的本质,而且更有利于学生的学习.从结构品读,收获教学智慧.给学生提供一个完整的认识数学基础知识的机会,为以后的高等数学学习奠定基础
2. “玩”好概念
概念是学科的基石. 李邦河院士曾说:“数学从根本上玩的是概念,而不是技巧. 技巧不足道也!”作为数学教师,必须“玩”好概念.
(1)认清定义的固有特性.
定义与定理虽一字之差,但固有特性截然不同. 定义必具充要性,而定理未必如此. 譬如,“两个函数相等”的定义表明:两个函数的定义域相同且对应关系相同是两个函数相等的充要条件,这既能当作函数相等的判定条件,又可以作为函数相等的性质;零点存在性定理揭示:函数f(x)在区间[a,b]上的图像是连续不断的一条曲线,且f(a)·f(b)<0是函数f(x)在区间(a,b)内有零点的充分条件. 由于不满足必要性,所以只能作为函数存在性零点的判定条件.
(2)理解概念的本质属性.
對数学概念的理解不能停留在表面,应深入到本质,否则极容易犯错误.
以上乃笔者之拙见,权当抛砖引玉,敬请同仁斧正!
参考文献:
[1] 刘绍学. 普通高中课程标准实验教科书数学必修1(A版)[M]. 北京:人民教育出版社,2007.
[2] 章建跃. 普通高中课程标准实验教科书数学第一册(A版)[M]. 北京:人民教育出版社,2020.
[3] 叶景辉,吴伟朝. 教材这样定义有问题吗?[J]. 中学数学杂志,2015(03):16.
作者简介:何业亮(1981—),本科学历,中学一级教师,马林名师工作室成员,校教研组长,市骨干教师,从事高中数学教学工作十余年.
