几个关于1-2有序分拆的恒等式及组合证明
2022-11-23郭育红
郭 育 红
( 河西学院 数学与统计学院, 甘肃 张掖 734000 )
0 引 言
在整数分拆理论中,MacMahon[1]第一次定义了正整数的有序分拆.即把正整数n表示成一些正整数的有序和,其中每一项叫该分拆的分部量.如果不考虑分部量的顺序就是无序分拆.例如,4的有序分拆有4,3+1,1+3,2+2,2+1+1,1+2+1,1+1+2,1+1+1+1或(4),(3,1),(1,3),(2,2),(2,1,1),(1,2,1),(1,1,2),(1,1,1,1)共8个,而无序分拆有5个:4,3+1,2+2,2+1+1,1+1+1+1.有序分拆的反分拆是把该分拆的分部量的顺序倒过来产生的分拆.例如,(1,1,2)的反分拆就是(2,1,1),它们互为反分拆.分拆α的反分拆用α′表示.
在经典的分拆理论中,分拆恒等式的研究一直是热点问题之一[1-3].近年来,许多研究者得到了丰富的研究成果[4-9].本课题组也得到了一些关于带约束的有序分拆恒等式[10-16].
通常把正整数n的分部量是1或者2的有序分拆称为1-2有序分拆,把正整数n的分部量是奇数的有序分拆称为奇有序分拆.
借助于正整数的带约束的有序分拆与特殊数列的关系,能够产生一些有趣的分拆恒等式.比如,正整数n的1-2有序分拆数等于正整数n+1的奇有序分拆数.寻找分拆恒等式一直是整数分拆理论研究中有趣的内容,但是,获得分拆恒等式或者给出分拆恒等式的组合证明仍然是比较困难的.
本文考察正整数的首、末两端分部量是1或者2的1-2有序分拆,给出这些有序分拆数与Fibonacci 数之间的一些关系式,进而,利用熟知的与Fibonacci数相关的有序分拆恒等式得到几个新的有序分拆恒等式,并给出组合双射证明.
1 预备知识
在文献[1]中,MacMahon给出了有序分拆的图表示,称为zig-zag图,类似于无序分拆的Ferres图,即将有序分拆每个分部量λi依次用含有λi个点的行来表示,但要求下一行的第一个点与上一行的最后一个点对齐.例如14的有序分拆(6,3,1,2,2)的zig-zag图如图1所示.

图1 Zig-zag图
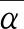
文献[6]中给出了关于正整数的分部量带约束的一些有序分拆数与Fibonacci数之间的关系式.所谓Fibonacci数是指满足以下条件的数:F1=1,F2=1,Fn=Fn-1+Fn-2,n>2.
下面以定理的形式给出文献[6]中几个熟知的关系式.
定理1[6]设正整数n的分部量是1或者2的有序分拆数为C1-2(n),则
C1-2(n)=Fn+1;n>0
其中Fn+1是第n+1个Fibonacci数.
定理2[6]设正整数n的分部量是奇数的有序分拆数为Codd(n),则
Codd(n)=Fn;n>0
其中Fn是第n个Fibonacci数.
定理3[6]设正整数n的分部量是大于1的有序分拆数为C>1(n),则
C>1(n)=Fn-1;n>1
其中Fn-1是第n-1个Fibonacci数.
2 主要结果
首先给出下面与分部量2有关的1-2有序分拆数和Fibonacci数的一个关系式.
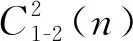
其中Fn是第n个Fibonacci数.
下面给出该定理的一个组合证明.
证明把正整数n的首、末两端的分部量至少有一个是2的1-2有序分拆分为下面两类:
(A)左端的分部量是2;
(B)左端的分部量是1.
对于(A)类中的任意一个分拆α=(2,a2,a3,…,ak),若ak=1,则直接删掉ak=1,就得到了n-1的首、末两端分部量至少有一个是2,且左端分部量是2的1-2有序分拆;若ak=2,则把左端的分部量2用1替换,就得到了n-1的首、末两端分部量至少有一个是2,且左端分部量不是2的1-2有序分拆.这样,就得到了n-1的首、末两端分部量至少有一个是2的1-2有序分拆.反之,对于n-1的首、末两端分部量至少有一个是2的任意一个1-2有序分拆β=(b1,b2,…,bs),其中b1、bs中至少有一个是2,若b1=2,则在β的右端添上分部量1,就得到分拆γ=(b1,b2,…,bs,1),则γ就是n的右端分部量是1的相应1-2有序分拆.若b1=1,此时bs=2,用b1+1替换b1,得到Δ=(2,b2,…,bs),则Δ就是n的右端分部量是2的相应1-2有序分拆.这样就说明了(A)类中的分拆与n-1的首、末两端分部量至少有一个是2的1-2有序分拆是一一对应的.
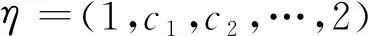
即

故结论成立.
□
由于正整数n的1-2有序分拆数等于Fn+1,利用Fibonacci数的性质,得到关于分部量1的1-2有序分拆的一个关系式.
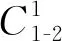
其中Fn-1是第n-1个Fibonacci数.
下面给出该关系式的一个组合证明.
证明把正整数n首、末两端分部量都是1的1-2有序分拆分为下面两类:
(A)第二个分部量是2,即α=(1,2,a3,…,ak,1);
(B)第二个分部量是1,即β=(1,1,c3,…,ct,1).
对于(A)类中的任意一个分拆α=(1,2,a3,…,ak,1),直接删掉第二个分部量2就得到了n-2的首、末两端分部量都是1的1-2有序分拆.反之,对于n-2的首、末两端分部量都是1的任意一个1-2有序分拆γ=(1,b2,…,bs-1,1),在前两个分部量1与b2之间添上分部量2,得到的分拆δ=(1,2,b2,…,bs-1,1),就是n的首、末两端分部量都是1的相应分拆.这样就说明了(A)类中的分拆与n-2的首、末两端分部量都是1的1-2 有序分拆是一一对应的.
对于(B)类中的任意一个分拆β=(1,1,c3,…,ct,1),删掉β的第一个分部量1,就得到了n-1的首、末两端分部量都是1的1-2有序分拆.反之,对于n-1的首、末两端分部量都是1的任意一个1-2有序分拆ζ=(1,c1,c2,…,cs-1,1),在ζ的左端添上分部量1,就得到了n的首、末两端分部量都是1,且左边至少有2个分部量1的1-2有序分拆.这样就说明了(B)类中的分拆与n-1的首、末两端分部量都是1的1-2有序分拆是一一对应的.
即

故结论成立.
□
进一步考察,得到下面与Fibonacci数相关的结果.
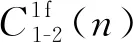
其中Fn是第n个Fibonacci数.
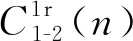
其中Fn是第n个Fibonacci数.
定理6与定理7的组合证明类似于定理5,故证明略.
下面给出定理6的一个例子.
例1设n=6,则6的首端分部量是1的1-2 有序分拆有下面8个:
(1,2,2,1),(1,2,1,1,1),(1,1,2,1,1),(1,1,1,2,1),(1,1,1,1,2),(1,1,1,1,1,1),(1,1,2,2),(1,2,1,2)
由定理6及定理1~3可得到下面的有序分拆恒等式.
推论1正整数n的首端分部量是1的1-2有序分拆数等于n的奇有序分拆数.
推论2正整数n的首端分部量是1的1-2有序分拆数等于n+1的分部量大于1的有序分拆数.
推论3正整数n的首端分部量是1的1-2有序分拆数等于n-1的1-2有序分拆数.
类似地,给出下面的恒等式.
推论4正整数n的末端分部量是1的1-2有序分拆数等于n的奇有序分拆数.
推论5正整数n的末端分部量是1的1-2有序分拆数等于n+1的分部量大于1的有序分拆数.
推论6正整数n的末端分部量是1的1-2有序分拆数等于n-1的1-2有序分拆数.
下面仅给出推论6的一个例子.
例2设n=6,则6的末端分部量是1的1-2有序分拆有下面8个:
(1,2,2,1),(1,2,1,1,1),(2,2,1,1),(1,1,2,1,1),(1,1,1,1,1,1),(2,1,1,1,1),(2,1,2,1),(1,1,1,2,1)
与5的以下8个1-2有序分拆一一对应:
(1,2,2),(1,2,1,1),(2,2,1),(1,1,2,1),(1,1,1,1,1),(2,1,1,1),(2,1,2),(1,1,1,2)
结合定理3和定理5,易得下面的有序分拆恒等式.
定理8正整数n的首、末两端的分部量都是1的1-2有序分拆数等于n的分部量大于1的有序分拆数.
利用有序分拆的共轭易知两类分拆之间存在一一对应关系,证明略.
由定理4和定理2可得到下面的恒等式.
定理9正整数n的首、末两端分部量至少有一个是2的1-2有序分拆数等于n的奇有序分拆数.
下面给出该定理的一个组合证明.
证明对于正整数n的首、末两端分部量至少有一个是2的任意一个1-2有序分拆α=(a1,a2,…,ak),若a1=1,此时ak=2,在α中,按照从左向右的顺序,将分部量1和其右边相邻的所有分部量2相加,产生的和作为新的分部量,这样得到的分拆就是n的左端分部量是1,右端分部量大于1的奇有序分拆.反之,对于n的右端分部量大于1的任意一个奇有序分拆,将大于1的奇分部量分拆成“1,2,2,…,2”的形式,就得到n的左端分部量是1,右端分部量是2的1-2有序分拆.
在α中,当a1=2时,分两种情形来讨论:
(a)右端的分部量ak=1;
(b)右端的分部量ak=2.
对于情形(a)中的任意一个分拆β=(2,a2,…,ak-1,1),首先将左端的分部量2分拆成“1,1”,得到分拆γ=(1,1,a2,…,ak-1,1),然后在分拆γ中按照从左向右的顺序,将分部量1和其右边相邻的所有分部量2相加,产生的和作为新的分部量,这样就得到n的左、右两端分部量都是1的奇有序分拆.反之,对于n的左、右两端分部量都是1的任意一个奇有序分拆,将大于1的奇分部量分拆成“1,2,2,…,2”的形式,然后将左端的两个相邻的分部量“1,1”相加,得到的2作为新的分部量,就得到情形(a)中的分拆.

两类分拆之间是一一对应的.
□
下面给出一个例子来说明定理9中的对应关系.
例3设n=6,则6的首、末两端分部量至少有一个是2的1-2有序分拆有下面8个:
(2,2,2),(2,1,1,2),(2,2,1,1),(1,1,2,2),(1,1,1,1,2),(2,1,1,1,1),(2,1,2,1),(1,2,1,2)
与6的以下8个奇有序分拆一一对应:
(5,1),(3,1,1,1),(1,3,1,1),(1,5),(1,1,1,3),(1,1,1,1,1,1),(1,1,3,1),(3,3)
类似地,由定理4、定理1和定理3得到下面的恒等式.
定理10正整数n的首、末两端分部量至少有一个是2的1-2有序分拆数等于n-1的1-2有序分拆数.
证明对于正整数n的首、末两端分部量至少有一个是2的任意一个1-2有序分拆δ=(r1,r2,…,rt),若rt=2,则用rt-1=1替换rt,就得到n-1的右端分部量是1的相应分拆.若rt=1,则r1=2,求δ的反分拆δ′=(rt,…,r2,r1),然后删掉δ′左端的分部量rt,就得到n-1的右端分部量是2的相应分拆.
反之,对于n-1的任意一个1-2有序分拆σ=(c1,c2,…,ck),若ck=1,则用ck+1=2替换ck,就得到n的右端分部量是2的1-2有序分拆;若ck=2,先在σ的左端添上分部量1,得到分拆τ=(1,c1,c2,…,ck),再求τ的反分拆τ′,则τ′就是n的右端分部量是1,左端分部量是2的1-2有序分拆.
故两类分拆之间一一对应.
□
定理11正整数n的首、末两端分部量至少有一个是2的1-2有序分拆数等于n+1的分部量大于1的有序分拆数.
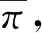
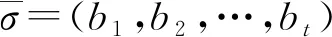
故两类分拆之间一一对应.
□
由定理4和定理6可得到下面的恒等式.
推论7正整数n的首、末两端分部量至少有一个是2的1-2有序分拆数等于正整数n的首端分部量是1的1-2有序分拆数.
证明对于正整数n的首、末两端分部量至少有一个是2的任意一个1-2有序分拆α=(a1,a2,…,ak),其中a1、ak至少有一个是2,若ak=1,此时a1=2,则求α的反分拆,就得到n的左端分部量是1,右端分部量是2的1-2有序分拆.若ak=2,分两种情况:当a1=2,将a1=2分拆成“1,1”,并把这两个1分别放在左、右两端;当a1=1,此时ak=2,将ak=2分拆成“1,1”.于是得到n的左、右两端分部量是1的1-2有序分拆.反之,对于n的任意一个首端分部量是1的1-2有序分拆β=(b1,b2,…,bt-1,bt),其中b1=1,若bt=2,求β的反分拆,就得到n的左端分部量是2,右端分部量是1的1-2有序分拆;若bt=1,分两种情况:当bt-1=1,把bt与bt-1合并得到的2作为右端新的分部量;当bt-1=2,把bt与左端的分部量b1合并得到的2作为左端新的分部量.于是得到n的右端分部量是2的1-2有序分拆.
□
由定理4和定理7可得到下面的恒等式.
推论8正整数n的首、末两端分部量至少有一个是2的1-2有序分拆数等于正整数n的末端分部量是1的1-2有序分拆数.
该推论的证明与推论7相同,故证明略.
下面给出推论8的一个例子.
例4设n=6,则6的首、末两端分部量至少有一个是2的1-2有序分拆有下面8个:
(2,2,2),(2,1,1,2),(2,2,1,1),(1,1,2,2),(1,1,1,1,2),(2,1,1,1,1),(2,1,2,1),(1,2,1,2)
与6的以下8个末端分部量是1的1-2有序分拆一一对应:
(1,2,2,1),(1,2,1,1,1),(2,2,1,1),(1,1,2,1,1),(1,1,1,1,1,1),(2,1,1,1,1),(2,1,2,1),(1,1,1,2,1)
3 结 语
在整数分拆理论中,分拆恒等式的研究一直是研究热点,而关于分部量带约束条件正整数有序分拆恒等式的研究还不是非常深入.本文主要考察了正整数的分部量是1或者2的有序分拆,尤其是正整数的首、末两端分部量是1或者2的1-2有序分拆,得到了这些有序分拆数与Fibonacci 数之间的一些关系式.进而,利用熟知的与Fibonacci数相关的有序分拆恒等式,得到了几个关于正整数的1-2有序分拆的新的有序分拆恒等式,并给出了组合双射证明.这些结果在理论上进一步丰富了整数分拆恒等式,同时也为寻找整数分拆恒等式的组合双射证明提供了一些方法.
