基于堆料面预测模型的电铲三维挖掘轨迹规划

2022-11-23黎柿汪，张天赐，付涛，李光，孙刚，宋学官*

大连理工大学学报 2022年6期

黎柿汪，张天赐，付涛，李光，孙刚，宋学官*

( 1.大连理工大学机械工程学院，辽宁大连 116024；2.太原重工股份有限公司矿山采掘装备及智能制造国家重点实验室，山西太原 030024 )

0 引言

大型电铲是露天矿山开采的关键设备，其产品性能和生产能力将直接决定矿山开采的效率[1-3]．传统的电铲主要依靠操作者的经验进行挖掘作业，存在以下问题：不同操作者进行作业的满斗率和挖掘效率有较大差距；挖掘现场粉尘大，作业环境恶劣，操作者视野差、视距远，再加上堆料面形貌特征丰富，操作难度大．因此，传统人工操作或是简单的挖掘自动化已经无法满足矿用电铲发展需求[4-5]．近年来，国家对露天矿场开采量需求的增加，使电铲具备感知能力和决策能力，提高电铲智能化水平迫在眉睫[5]．

计算合适的挖掘轨迹是电铲智能化的基础问题[6]，针对智能挖掘机的挖掘轨迹规划，国内外学者做了大量研究．Kim等[7]提出一种以最小化转矩为优化目标的算法，将得到的轨迹与经验丰富操作者的实际挖掘过程进行比较，减少了作业过程的转矩，但该方法未考虑挖掘时间、挖掘能耗等性能指标．Wang等[8]基于高次多项式描述挖掘轨迹，结合动力学模型，并考虑多种堆料面形貌特征，实现了能耗最优的挖掘轨迹规划．然而，该方法在规划时只考虑了堆料面的截面曲线特征，未考虑堆料面的三维形貌特征．孙志毅等[9]提出了4-3-3-3-4关节角度分段多项式插值策略，通过确定中间位姿点，以关节角速度与角加速度为约束，在避免产生较大冲击的同时，实现了时间最优轨迹规划．孙祥云等[10]通过约束铲斗姿态角，利用三次多项式插值法对挖掘轨迹进行插值，并在考虑各运动关节最大速度的约束下，以齿尖运动路径最短为优化目标使用粒子群算法进行挖掘轨迹规划，通过分析实验结果，证明规划得到的轨迹提升了挖掘机工作效率．通过以上分析可知，现有工作大部分集中在理论分析，未能将环境感知与自主决策有机结合，更没有实际的无人电铲产品．

为解决以上问题，本文以太原重工股份有限公司生产的WK-55型电铲1∶7缩比样机为研究对象，搭建无人挖掘系统．然后，提出一种基于堆料面预测模型的电铲三维挖掘轨迹规划方法．本文所提出的挖掘轨迹规划方法首先通过激光雷达扫描料场采集点云，基于多项式响应面(polynomial response surface，PRS)法建立堆料面预测模型，将三维堆料面形貌特征考虑入轨迹规划；其次，通过拉格朗日方程建立电铲工作装置动力学模型，用于力的计算；然后，使用高次多项式对挖掘轨迹在时间域进行插值，将轨迹寻优问题转化为多项式系数寻优问题；最后，将挖掘时间作为优化变量，满斗率、速度、力等作为约束，以单位最小能耗为优化目标，建立轨迹优化模型，进行挖掘轨迹规划．

1 堆料面预测模型

面上自主挖掘开发的样机如图1所示，在所配备的硬件系统中，电气控制柜包括电源转换模块、PLC控制系统等，其中PLC控制系统相当于下位机，用于在接收上位机发送的电机控制信号以及操作模式信号后对电铲进行自动控制，完成移动、挖掘、回转、卸料、复位等动作；激光雷达用于获取周围环境的点云信息，以实现根据不同形貌堆料面采用不同的轨迹进行合理挖掘；推压机构上安装倾角传感器，用于测量斗杆倾角；IMU+GPS+各个电机上的编码器+倾角传感器用于获取电铲姿态信息，是环境感知、运动规划以及反馈控制的前提条件；移动工作站为样机自主决策所需的上位机，负责进行环境感知和运动规划等所需运算．

1 大臂；2 提升绳；3 推压机构；4 斗杆；5 铲斗；6 数据采集系统；7 移动工作站；8 电气控制柜；9 IMU；10 GPS；11 提升机构；12 激光雷达

基于激光雷达采集的点云建立堆料面模型，可以让电铲具备与环境进行交互的能力，是电铲智能化过程中十分重要的一步．堆料面建模问题实际上就是曲面建模问题，在实时自主挖掘中需考虑时间与精度的平衡．对于电铲智能化场景来说，实时性是第一要素，所建立的堆料面模型在保证足够精度要求前提下，应尽可能地减少建模以及寻优时进行挖掘体积计算两方面的时间．传统的点云模型重建方法——MC算法[11]和滚球法[12]虽然具有较高重建精度，但由于计算时间过长难以应用于实时堆料面建模与预测中．PRS[13]法作为一种近似建模方法，可以通过解析方法获得堆料面数学表达式，满足精度与建模时间要求的同时，大幅降低预测时间，故本文采用PRS法建立堆料面模型．

利用PRS法建立的堆料面模型是一个二元高阶多项式曲面方程S(x，y)，具体如下：

(1)

(2)

其中B为x和y组成的范德蒙矩阵，U为多项式系数向量，H为样本输出值列向量，代表点云数据z值．PRS法建模的目的是为了找到最优的多项式系数U使如下损失函数最小：

L=(H-BU)T(H-BU)

(3)

多项式系数U可使用最小二乘法求解，可得：

U=(BTB)-1BTH

(4)

2 动力学模型

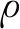
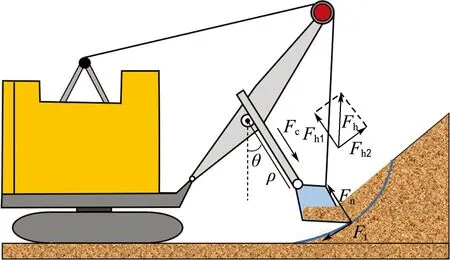
图2 工作装置广义坐标及受力分析

根据两个广义坐标，可得拉格朗日动力学方程：

(5)

式中：Lh为斗杆长度；Ld为铲斗长度；Fh为提升力；Fc为推压力；Fn为挖掘径向阻力；Ft为挖掘切向阻力；g为重力加速度；ϖ为提升绳与推压杆之间的夹角；mh为斗杆质量；md为铲斗质量，包括自身质量与物料质量．

3 轨迹优化模型

建立轨迹优化模型，需要确定优化三要素：优化变量、目标函数以及约束函数．在每一次挖掘作业之前，通过分析激光雷达扫描得到点云信息，然后在轨迹优化模型基础上，选用合适的优化算法进行寻优，可得当前工况下的最优挖掘轨迹．

3.1 挖掘轨迹选型

电铲在三维空间进行挖掘运动时，其挖掘轨迹会形成一个挖掘轨迹面，但由于前端工作装置是一个二自由度机械臂，该挖掘轨迹面在与铲斗宽度平行的方向为一条挖掘轨迹曲线，故可在铲斗宽度方向上将挖掘轨迹面离散成多条挖掘轨迹线，如图3所示．由此而来，可在每个挖掘轨迹线所在的二维空间进行挖掘轨迹规划，综合所有挖掘轨迹线的规划结果作为整个挖掘运动的规划结果，从而将三维挖掘轨迹规划问题转化为二维挖掘轨迹规划问题．

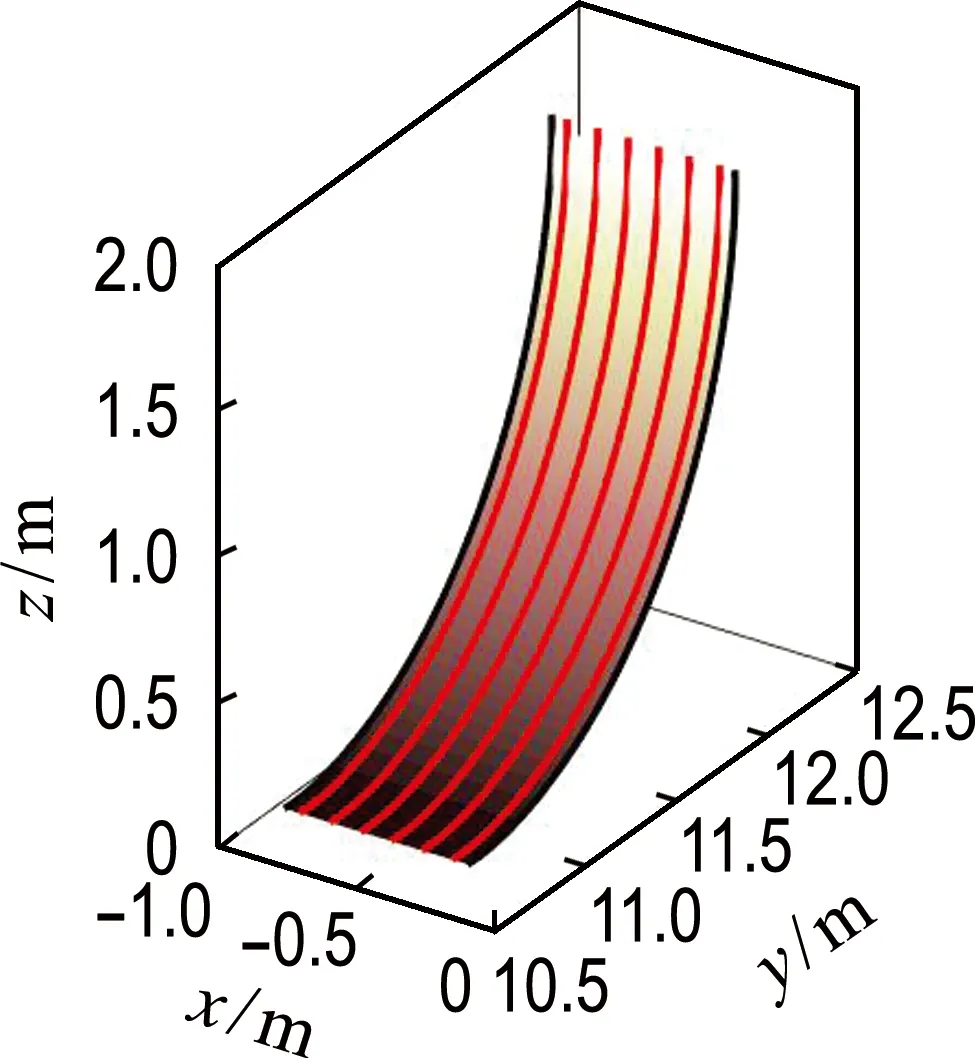
图3 挖掘轨迹面离散方法

每条挖掘轨迹线在二维空间的表达式是一致的，在二维空间内，将挖掘轨迹分解成x和y方向上的轨迹，并确定电铲的起始状态和终止状态，再使用高次多项式在时间域对挖掘轨迹进行拟合．挖掘轨迹所处的笛卡儿坐标系如图4所示．根据Wang等[8]所做的对比实验，以能耗最优为优化目标时的最佳多项式最高次数为6，同时低的次数能够减少优化变量的数量，在减少寻优时间的同时提高算法鲁棒性，故本文选取6次为两方向多项式最高次数．在6次多项式中，0～5次多项式系数ai0～5(i=x，y)可由第6次项系数、挖掘时间以及初始和终止条件确定[16]，从而将一个复杂的挖掘轨迹寻优问题转化为寻找最优多项式系数组合问题．挖掘轨迹在x、y方向上的表达式如下所示：

图4 挖掘轨迹所处坐标系

sx(t)=ax6t6+ax5t5+…+ax2t2+ax1t+ax0

sy(t)=ay6t6+ay5t5+…+ay2t2+ay1t+ay0

(6)

根据挖掘轨迹，可通过第2章所建立的动力学模型进行动力学求解得到挖掘过程中的推压力和提升力．

3.2 挖掘体积计算

已知第1章所述的堆料面预测模型S(x，y)和图3所示的挖掘轨迹面T(x，y)，可通过二重积分进行挖掘体积计算．挖掘体积计算涉及如图3所示的三维轨迹的二维切分，以及规划所得的多条二维轨迹的离散点向基坐标系的坐标转换，是本文所述方法将二维轨迹规划转化为三维轨迹规划的关键．

挖掘体积计算方法如图5所示．先利用一组网格将积分区域Dxy离散成k个封闭区域Δσi．当Δσi很小时，可在Δσi内任取一点(ζi，ηi)，以[S(ζi，ηi)-T(ζi，ηi)]Δσi为底计算每个柱体体积，然后累加得到挖掘体积，如下所示：

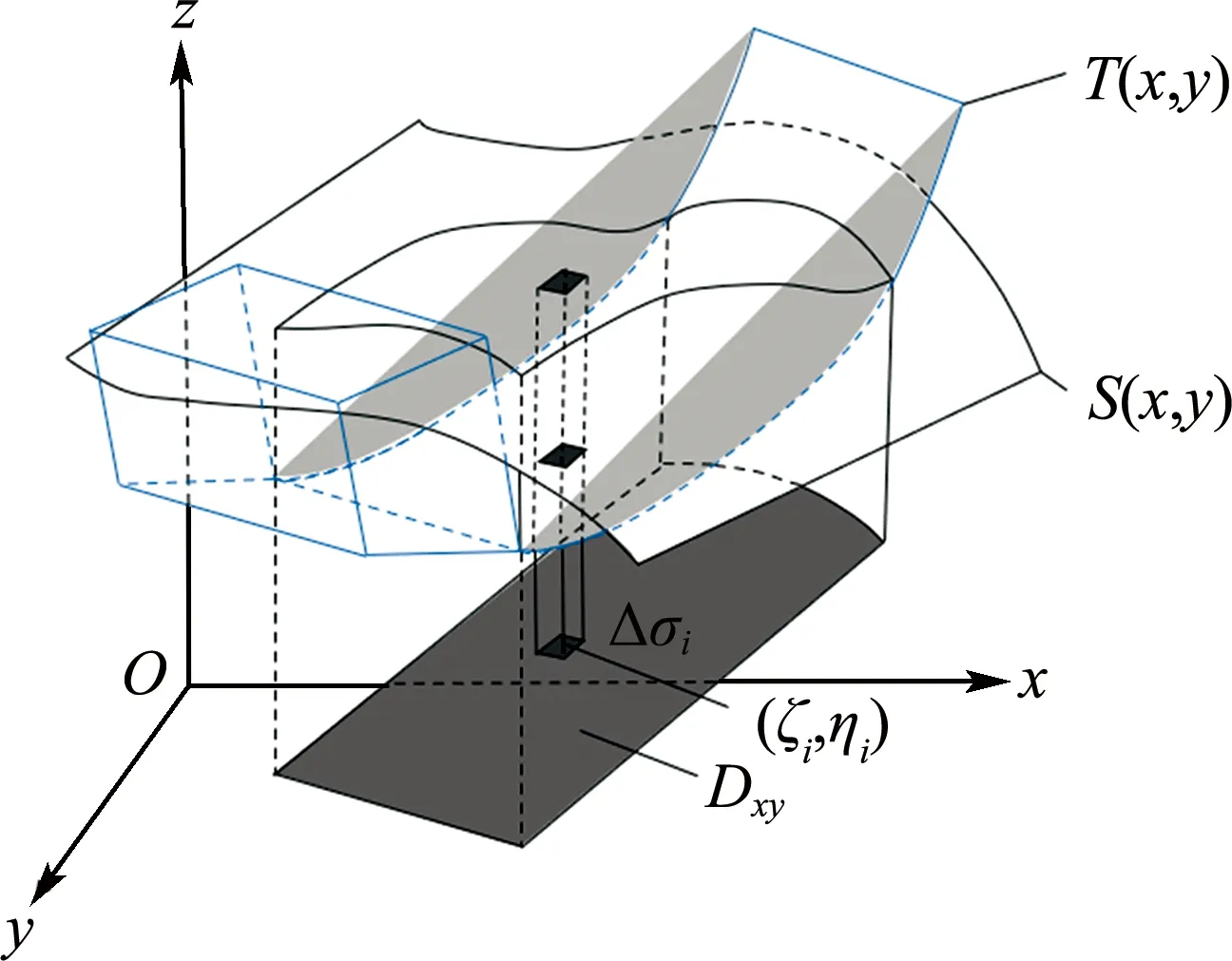
图5 挖掘体积计算方法

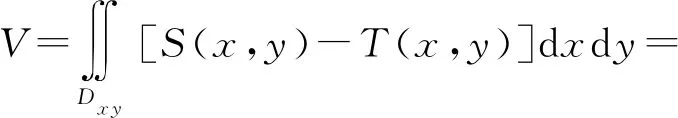
(7)

3.3 优化变量设计

为使铲斗的挖掘过程平滑且结束后能顺利停稳，初始点、终止点的速度和加速度均为0，同时铲斗在x和y方向上的初始位置均为0．在上述条件下，有3类轨迹参数影响挖掘性能，分别为挖掘时间、挖掘末端时刻终止位置以及多项式系数．设挖掘时间为t1，挖掘末端时刻终止位置x和y方向的坐标分别为sx(t1)和sy(t1)．由于x和y方向上6次多项式轨迹的前5次项系数ai0～5(i=x，y)可由第6次项系数ai6(i=x，y)、挖掘时间t1以及sx(t1)和sy(t1)确定，故需优化的多项式系数变为2个，分别为ax6和ay6．

综上，挖掘轨迹规划优化变量为

x=(ax6ay6sx(t1)sy(t1)t1)

(8)

3.4 目标函数确定

本文进行挖掘轨迹规划时，寻优的首要目标是“省”．为实现低能耗挖掘，以一次挖掘运动的单位体积挖掘能耗为目标建立目标函数：

(9)

其中Wh为提升电机能耗，Wc为推压电机能耗，通过下列积分表达式计算得到：

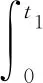
(10)

(11)

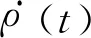
基于实际应用需求，以及所确定的优化变量和目标函数，将一个轨迹规划问题转化为基于多个不等式约束的非线性优化问题．因此轨迹优化模型可由下式表达：

(12)

3.5 约束函数确定

为保证规划所得的轨迹具有工程可用性，轨迹优化模型需要引入一些约束．轨迹优化模型所考虑的约束主要分为物理几何约束(g1～g3)和电铲性能约束(g4～g13)．

挖掘中铲斗底部的最小竖直高度应大于0，以确保不与地面发生干涉：

g1=-hbmin≤0

(13)

其中hbmin为挖掘过程中铲斗底部竖直高度的最小值．

为保证铲斗在挖掘过程结束后能无碰撞地进行回转运动，挖掘轨迹终点sy(t1)需高于对应的物料竖直高度：

g2=zm-sy(t1)≤0

(14)

其中zm为挖掘轨迹终点对应的物料竖直高度．

挖掘过程中斗杆伸长量的最大值应限制在一定范围：

(15)

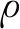
为保证满斗率，同时避免挖掘过载和欠载，样机铲斗挖掘体积应限制在一定范围内．这里设置铲斗容积Vd的90%和110%作为单铲挖掘体积的下、上界：

g4=0.9Vd-V≤0
g5=V-1.1Vd≤0

(16)

考虑提升电机和推压电机的实际转速限制，挖掘过程中最大提升速度和推压速度不应大于设计值：

(17)

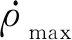
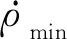
(18)

为确保挖掘的可执行性，挖掘提升力、推压力、提升功率和推压功率的最大值Fhmax、Fcmax、Phmax和Pcmax不得超过相应电机的额定值：

g10=Fhmax-Fha≤0
g11=Fcmax-Fca≤0
g12=Phmax-Pha≤0
g13=Pcmax-Pca≤0

(19)

其中Fha、Fca、Pha和Pca分别表示提升力、推压力、提升功率和推压功率的最大允许值．约束中的相关参数取值见表1．

表1 约束相关参数

4 实验分析

4.1 预测模型阶数选择

对于PRS法预测模型来说，唯一的控制变量在于多项式的阶数．本文将通过使用多组处理后的堆料面点云进行实验，确定最合适的PRS法模型阶数，使得建模时间和精度都能够满足实时轨迹规划的要求．

在进行堆料面建模之前，需先将激光雷达得到的料场点云进行配准，然后将配准后的料场数据中的堆料面点云分割出来，再进行接下来的工作．图6(a)为配准后的料场点云，图6(b)为分割后的堆料面点云．

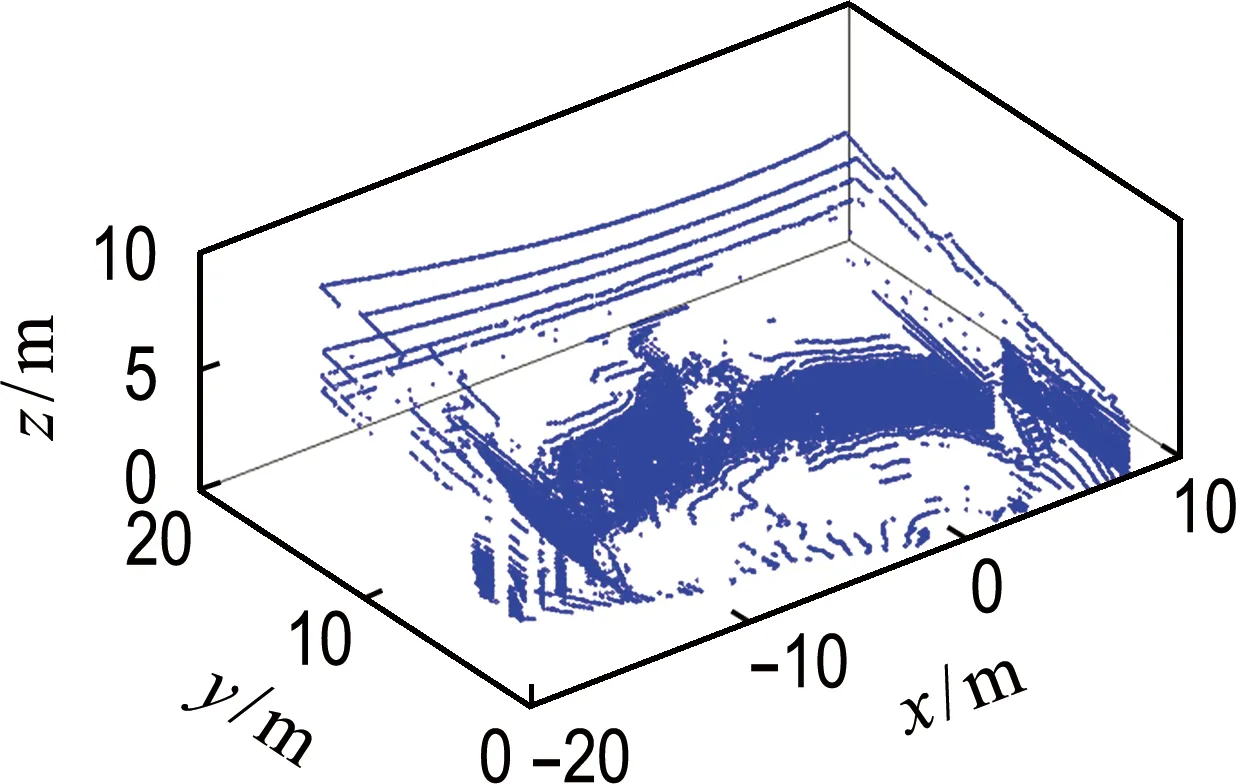
(a) 料场点云

实验采用多组形貌特征不同的点云，使用2～10阶作为阶数变量进行PRS法预测，从建模时间、预测时间和拟合精度3个方面分析结果并选择模型最佳阶数．为了定量计算拟合精度，本文使用系数R2[17]作为度量指标，计算方法如下：

(20)

实验将整幅点云同时用于建模和预测，从而计算R2．每组点云在阶数一定的情况下，得到的建模时间、预测时间以及R2均为进行5次实验结果的平均值，点云的点数及实验结果如表2所示．

表2 不同点云各模型阶数建模结果对比

点云3包括建模所需的最大点数以及足够丰富的形貌特征．实验中发现，这两个方面最有可能为影响模型建模速度以及精度的潜在因素．从点云3的R2列可得，只有高于6阶时，模型才能满足大于95%的精度要求．由点云1～3的6～10阶R2结果可得，在6阶之后模型的精度提升只有1%～1.7%，但时间最多可以相差0.03 s，而模型需求是在低于0.05 s的前提下尽可能小，在8阶以后存在建模时间超过0.05 s的情况，可以把最优阶数锁定在6～8阶；再看预测时间，6阶的预测时间最为稳定，呈倍数增长，但到7阶的时候时间增长速度比原先的倍数增长更快．故综合考虑建模时间、预测时间、R23个方面，6阶为最合适的模型阶数．图7为6阶PRS法模型对3组点云进行预测得到的堆料面模型．

(a) 点云1(8 651个点)

4.2 样机实验

实验使用COBYLA算法[18]作为轨迹寻优算法．之所以选择该算法，是因为该算法为C++标准非线性优化库NLOPT中的算法，便于开发；通过将其规划结果与MATLAB中遗传算法的规划结果对比发现，结果基本一致；能在大多数工况下在300步内收敛到一个最优值，算法寻优时间可控制在3 s内，保证实时性的同时鲁棒性较强．

考虑电铲实际运动控制中电机采用速度控制，本文选择推压电机和提升电机的转速作为两个控制参数．通过激光雷达扫描物料面采集点云，在上位机建立物料面预测模型并通过挖掘轨迹规划得到最优轨迹后，根据电铲传动比计算电机转速，将规划所得转速通过PLC控制系统以10 Hz的发送频率传送给变频器，通过变频器控制电铲进行挖掘运动．算法规划结果如表3所示，可以看出规划出的结果均在合理范围内．图8给出了料场点云、堆料面模型以及实际料场环境下规划出的挖掘轨迹．图8(a)中红线为离散的挖掘轨迹，黄线为挖掘轨迹对应于堆料面上的曲线；从图8(b)中可看到推压速度比提升速度先到达最大值，这是因为挖掘运动需先朝里挖到一定深度，再通过提升拉起物料；从图8(c)、(d)中可看到所规划的力和功率都能够满足约束．

表3 算法规划结果

(a) 挖掘轨迹及剖面图

智能化电铲单次自主挖掘过程如图9所示．图9(a)所示为电铲在一个初始位置扫描物料面获得挖掘位置；图9(b)、(c)和(d)分别为电铲挖掘起始、挖掘中和结束时刻状态；图9(e)、(f)分别为电铲的回转和卸料过程．当装载完成后，激光雷达正对物料面点云开始第2次扫描，并在回转和位姿初始化过程中上位机多线性地计算下一次的最优挖掘轨迹，从而保证无人自主挖掘作业的连续性．控制电铲的实际电机转速与规划所得的输入转速对比如图10所示，实际与规划的力对比如图11所示．

(a) 初始位置

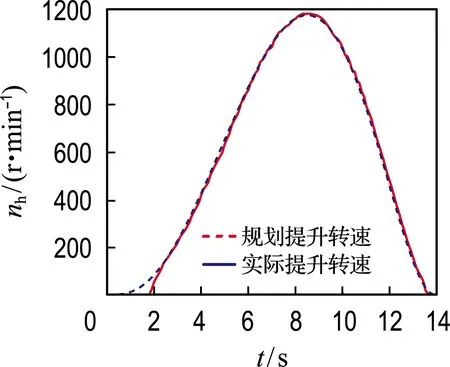
(a) 实际与规划提升转速对比

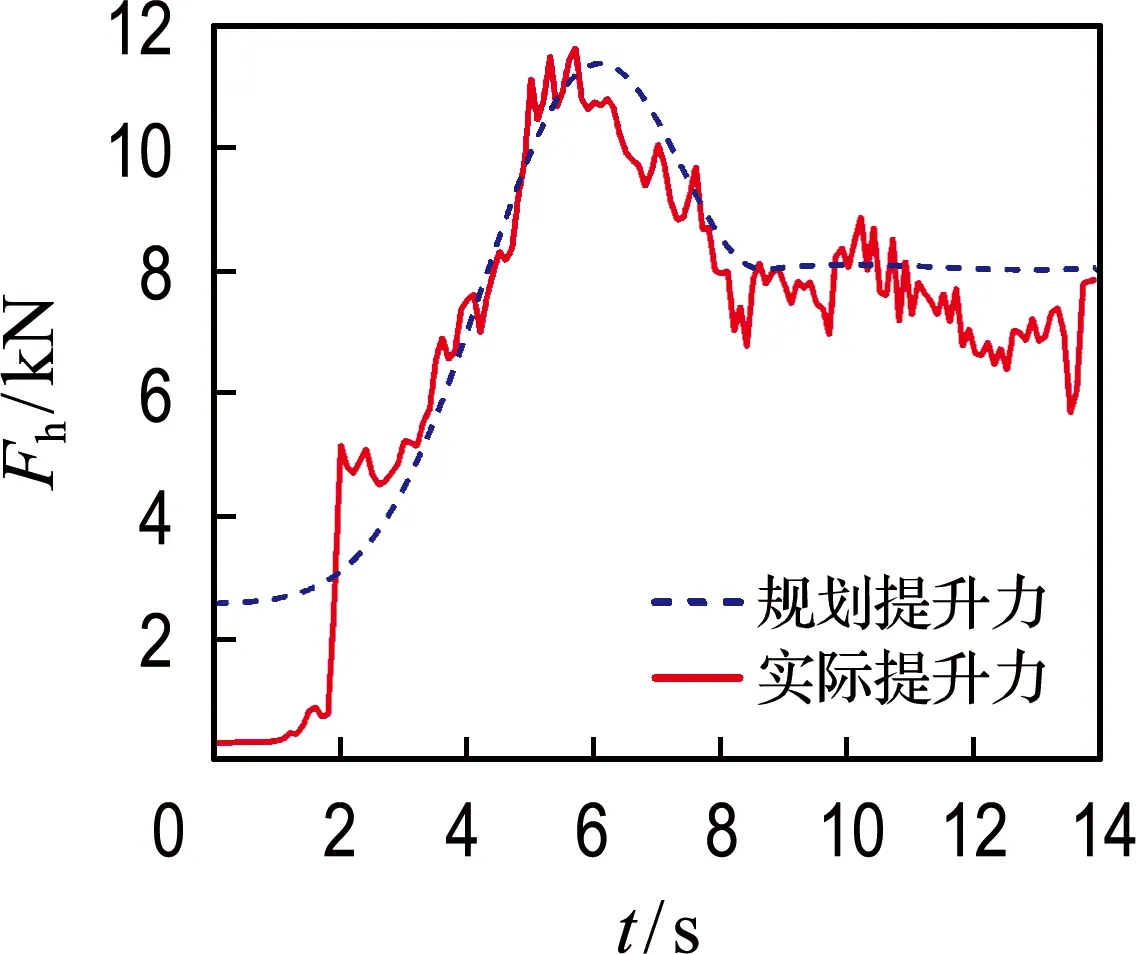
(a) 实际与规划提升力对比

由图10可知，两电机转速起始和接近终点时会出现跟随不上的情况，这是由于起始和接近终点时输入转速过小，电机无法跟随；提升转速基本上跟随上了，但推压转速在3～8 s时出现抖动，这是由于在挖掘过程中遇到了一些稍大石块，导致推压方向上力与位移的突变．从图11可知，实际力比规划力的抖动更剧烈，但数值相差不大，而且总的变化趋势一致．表4为实际与规划的能耗和挖掘体积，其中Wph和Wah分别代表规划提升电机能耗和实际提升电机能耗，Wpc和Wac分别代表规划推压电机能耗和实际推压电机能耗，Vp和Va分别代表规划挖掘体积和实际挖掘体积．从表中可见，所提方法对能耗以及挖掘体积计算较为准确，能够满足满斗率需求．总的来说，本文提出的挖掘轨迹规划方法规划所得电机转速可以被电铲控制系统跟随，有效控制电铲进行挖掘作业，且所建立动力学方程用于动态输出力预测较为准确，对各性能指标的计算结果较为可靠．