城市景观桥梁施工中结构计算与BIM技术的融合路径分析

蒲国柱

（厦门市市政工程设计院有限公司，福建 厦门 361008）

0 引言

城市景观桥梁施工中的结构计算既是一项复杂的多学科计算技术，也是一种施工管理和管控的计算技术。该计算作业涉及面广、针对性强、计算量大，而传统计算方法存在各专业单一、独立等问题，设计人员无法及时展开交流，存在信息共享滞后、信息不直观和容易出现计算误差等弊端。而BIM 技术具有信息共享性和传递性的特点，可根据桥梁施工信息，自动对前期数据进行计算，不仅能够减少人工计算量，而且能降低计算误差，因此研究BIM 技术与桥梁施工中结构计算的融合路径，对缩短施工周期、推动施工作业有序展开有重要意义。

1 城市景观桥梁项目概况

1.1 概况

A 健康步道景观提升工程是S 市中北部的重要生态节点，该健康步道贯穿S 市东西方向山海步行通廊，全长约23.9km，分为主线段和节点桥梁段，其中主线段总长约22.1km，地面步道12.6km，新建林中贴地步道3.7km，改造地面步道3.4km，利用现状地面步道5.5km[1]。节点七桥梁为景观人行桥，全桥平面为直线，主跨度为90m，桥面全宽4.4m，桥面净宽3.8m，两端引桥分别长15.55m 和50m。主跨桥梁采用张弦桁架结构体系，由钢桁架作为上弦，下部设置双柔性缆索，中间连以外倾撑杆形成整体受力自平衡体系，撑杆外倾可增加桥面横向刚度，体系简单，受力明确。图1为桥梁立面图。

1.2 BIM 参数化模型建立

基于Rhino 平台，利用Grasshopper 插件构建节点七桥梁BIM 模型，结合“自底向上”和“自顶向下”两种BIM 建模方法。其中“自底向上”建模方法具体是指先构建桥梁基础构件，然后根据桥梁构件的位置关系，完成桥梁的基本结构组装，最后将多个桥梁基本结构组合成一个完整的结构；“自顶向下”具体是指先构建桥梁整体结构，然后将桥梁整体结构划分为不同的基本结构，再将基本结构拆分为不同构件进行设计，最后将桥梁拼装为整体结构。

由于节点七桥梁BIM 模型中包含多个附属结构，在对其进行分析和计算的过程中会受时间和计算机配置的限制，即构建精细化的桥梁模型需要花费大量的时间成本，而计算桥梁结构时，只需要构建桥梁的重要受力构件。因此，需要在BIM 模型的基础上对其进行简化，桥梁模型如图2所示[2]。

2 计算荷载及组合

2.1 永久作用

一期恒载：拱肋自重只考虑结构重力、预加力、土的重力与侧压力，不考虑混凝土收缩徐变、基础变位及水浮力。

二期恒载：结构自重及铺装重量按实计算，栏杆重量为每侧0.4kN/m；桥面钢格栅荷载为1kN/m2。

基础变位：桥梁拱座基础沉降以5mm 为标准考虑。

收缩徐变：桥梁施工完成后十年出现收缩徐变。

2.2 可变作用

2.2.1 人群荷载

根据《城市桥梁设计规范》（CJJ 11—2011）相关规定，桥梁不同加载长度下人群荷载如表1所示。

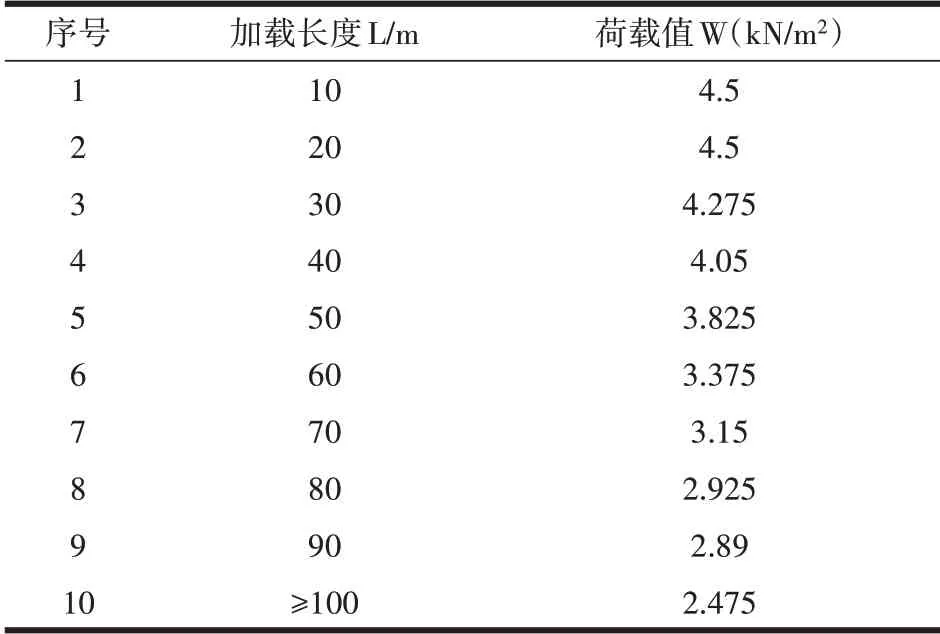
表1 人群荷载

由表1，90m 主桥加载长度人群荷载2.89kN/m2，10m 引桥加载长度人群荷载为4.5kN/m2，50m 引桥加载长度人群荷载为3.825kN/m2。

2.2.2 温度荷载

体系温度：桥梁结构体系整体升温为26℃，降温为-29℃。

温度梯度：按照桥梁单侧升温为5℃考虑。

温度组成形式：升温组合，结构体系升温+拱肋升温；降温组合，结构体系降温+拱肋降温[3]。

2.2.3 风荷载

《公路桥梁抗风设计规范》（JTG/T 3360-01—2018），桥梁基本风速按V10=46.7m/s 考虑。设计基准风速值为62.58m/s；静阵风风速为79.79m/s；主桁架横向风荷载为1.79kN/m；缆索的风荷载按直径规范计算。

2.3 地震作用

S 市抗震设防烈度为7 度，基本地震加速度为0.15g，地震分组为第三组，设计特征周期为0.45s；抗震时张弦梁桥阻尼比取0.02；E1 地震的水平向地震峰值加速度为0.069g，E1 地震反应谱最大值为0.1553g；E2 地震的水平向地震峰值加速度为0.3075g，E2 地震反应谱最大值为0.6919g。

3 桥梁结构静力计算

3.1 计算模型

由于桥梁主缆采用索单元模拟，桁架杆件用梁单元模拟，因此采用几何非线性方法进行结构计算，桥梁计算模型如图3所示。

3.2 主桥成桥状态与缆索线形计算

根据挠度控制可以计算出桥梁缆索初始索力，在计算模型上施加初始索力和恒载作用，可以获得桥梁成桥状态预内力与几何形状。另外，由于该桥梁工程二期恒载较小，仅为格栅桥面、栏杆及少量灯具，因此与一期恒载一起计算。桥梁成桥状态结构轴力图如图4所示[4]。

3.3 主桥各工况静力计算

3.3.1 结构内力

（1）工况内力

桥梁结构工况内力采用几何非线性方法进行计算，不同桥梁结构荷载工况下，内力主要有以下规律：主桁架和缆索之间为闭环系统，在不同荷载下，主缆与主桁架的轴力和撑杆轴力均匀性较好；竖向荷载为桥梁总体控制荷载，撑杆轴力、缆索拉力和桁架弦杆轴力与桥梁竖向荷载呈正比例关系；桥梁恒载为竖向荷载的65.5%，匀布活荷载为主桁架的控制荷载[5]。

（2）组合内力

桥梁结构荷载组合构件包络内力如表2所示。

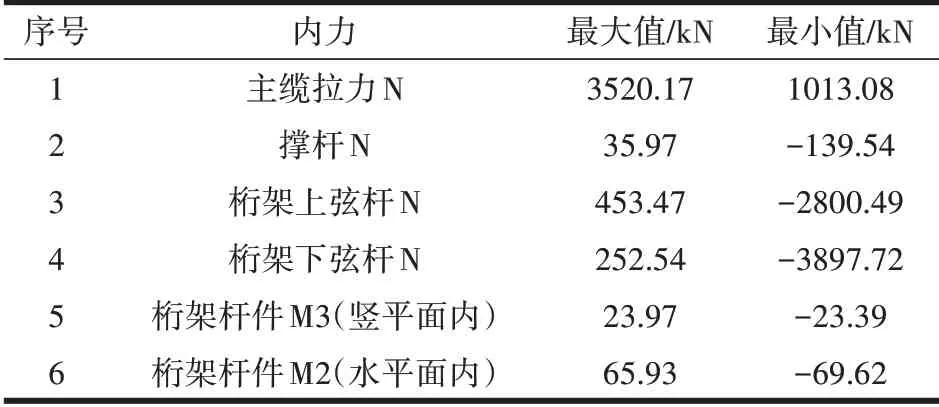
表2 桥梁结构荷载组合构件包络内力

根据表3可知，桥梁主缆拉力内力的最大值为3520.17kN，最小值为1013.08kN；撑杆内力的最大值为35.97kN，最小值为-139.54kN；桁架上弦杆内力的最大值为453.47kN，最小值为-2800.49kN；桁架下弦杆内力的最大值为252.54kN，最小值为-3897.72kN，可见主缆一直处于受拉状态不会松弛。

3.3.2 构件验算

表3所示内容为桥梁缆索、撑杆、桁架上弦杆和桁架下弦杆构件应力统计情况。

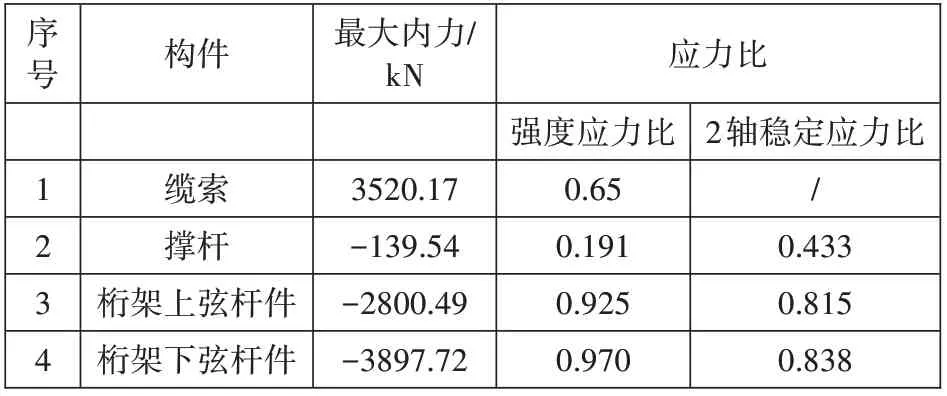
表3 构件应力统计表

由表3，桥梁缆索的最大内力为3520.17kN，强度应力比为0.65；撑杆的最大内力为-139.54kN，强度应力比和2 轴稳定应力比分别为0.191、0.433；桁架上弦杆的最大内力为-2800.49kN，强度应力比和2 轴稳定应力比分别为0.925、0.815；桁架下弦杆的最大内力为-3897.72kN，强度应力比和2 轴稳定应力比分别为0.970、0.838，说明桥梁所有构件的强度和稳定性满足桥梁设计规范要求，且有一定富余量。

3.3.3 支座反力与位移

表4所示内容为桥梁主桥结构4 个支座反力和平移统计情况。

从表4中可以看出，桥梁节点1 在X 轴方向的反力为32.03～-1303.54kN，在Y 轴上的反力为0kN，支座在三个方向上未出现平移情况；节点2 在X 轴方向上的反力为31.8～-1315.8kN，在Y 轴方向上的反力为0～-307.6kN，在三个方向上均未出现平移情况；节点3 在X 轴和Y 轴方向上的支座反力均为0kN，在X 轴上的平移距离为-55.4mm，并未在Y 轴和Z 轴方向上发生平移；节点4 在Y 轴上的反力为-244.3～0kN，在X 轴方向上的平移距离为-56.0mm，未在Y轴和Z 轴方向上发生平移[6]。

表4 支座反力和平移统计表

3.3.4 主桥静力弹性整体稳定性计算

根据主桥结构活荷载+恒荷载标准组合，利用非线性方法计算桥梁结构无缺陷整体情况下的弹性极限承载力，表5所示内容为桥梁结构整体承载力系数。

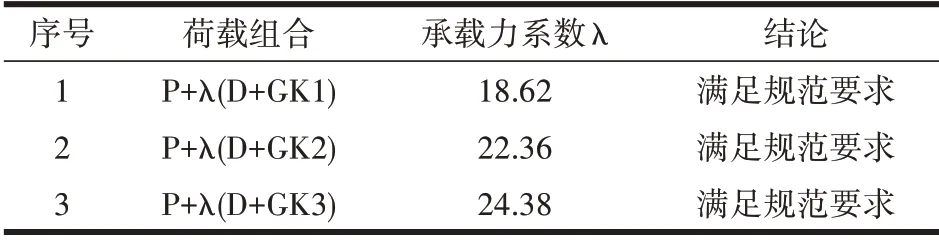
表5 桥梁结构整体承载力系数表

从表5中可以看出，桥梁D+GK1 工况组合承载力系数为18.62；D+GK2 工况组合承载力系数为22.36；D+GK3 工况组合承载力系数为24.38。所有工况组合承载力系数均大于《公路悬索桥设计规范》（JTG/T D65-05—2015）的要求，且桥梁整体承载力系数有富余量。

4 结语

以A 健康步道景观提升工程节点七桥梁计算应用为例，利用BIM 技术构建桥梁计算模型，并根据桥梁计算荷载及工况组合等相关数据，对桥梁结构静力进行计算，结果表明，BIM 技术在桥梁结构计算中有较强的适用性，此举也验证了BIM 技术在桥梁结构计算中的优势。综上可知，该技术不仅能进一步提高桥梁工程的施工效率、施工质量，也能有效避免结构计算误差所造成的施工成本增加问题，同时能为桥梁工程的有序、顺利开展提供有力的数据支持。