一种改进的基于正交表的异方差估计方法

郭雅静，张晓琴

(1.河北建筑工程学院 数理系，河北 张家口 075024；2.山西财经大学 统计学院，山西 太原 030006)

0 引言

经典的线性回归[1]都是以随机误差项的同方差性为前提的，但在实际应用中，随机误差项通常具有异方差性[2]，这使得应用普通最小二乘法得到的协方差阵估计不能保证其无偏性。因此，异方差的存在会对线性模型的分析造成影响。

随机误差项的协方差阵已知时常用广义最小二乘法[3](简记为GLS)来解决异方差问题。但多数情况下其协方差阵未知，为了估计随机误差项的协方差阵，学者们提出了极大似然估计法[4]，Box-Cox变换法[5]，贝叶斯估计法[6]，两阶段最小二乘估计[7-9]等方法。

异方差一致协方差阵估计(简称HCCMES)的提出直接给出了参数向量协方差阵的一致性估计，例如，White[10]于1980年提出的HC0估计效果很好且应用广泛，但是仅限于大量样本下使用。 为了解决小样本下的估计，在HC0基础上提出了HC1、HC2和HC3[11]3种估计。由于样本中的杠杆点会影响检验效果，Cribari-Neto[12]等人提出的HC4估计很好地消除了高杠杆点的影响。随后Cribari-Neto提出的HC5估计[13]和HC4m估计[14]分别解决了杠杆程度较高和较低情况下的估计问题。Li等[15]在2016年提出的HC5m估计将以上检验方法进行统一，并证明了其在检验中的优越性。

2015年，Zhang等[16]基于正交表提出一种一种稳定有效的异方差估计方法，称为OR方法。随后，提出的OR1方法[17]修正了OR方法中因变量的选择以及容差选取的缺陷。考虑到在异方差形式未知的情况下[18-19]，Carroll[20]提出的方差非参数估计具有较好的性质，本文在用正交表扩展后的模型中引入了方差的核估计[21-22]，进一步改进了OR1方法，称之为M-OR1方法。

本文的结构如下：第1节对异方差模型[23]进行简要的介绍。第2节介绍基于正交表的OR方法和OR1方法，并结合非参数方法提出了一种改进的OR1方法——M-OR1估计。第3节通过模拟实验和实际应用证明了M-OR1估计的优越性。第4节，进行了简要的总结并给出进一步的研究方向。

1 异方差模型

假设自变量xi=(xi1,xi2,…,xip)和因变量yi(i=1,2,…,n)满足如下线性回归模型：

(1)

写成矩阵形式为：

(2)

其中，

(3)

2 M-OR1方法

本节首先对已有的OR和OR1方法进行简单介绍，其次，回顾了Carroll在1982年提出的核估计，最后，在OR1方法中引入核估计进而提出了改进的OR1方法。

2.1 OR和OR1估计

Zhang等[16]首次提出了一种基于正交表的异方差估计方法(OR方法)，具体步骤如下：

在异方差模型(2)中，假设有3个自变量，即p=3。

1) 在数据集(xi1,xi2,xi3,yi),i=1,2,…,n中，对每个给定的i，将xi1,xi2,xi3,yi分别看作一个因子，其容差分别取作Δ1xi1,Δ2xi2,Δ3xi3,Δyi，一般地，取Δ1=Δ2=Δ3=Δ=0.01或0.001。则可按正交表L9(34)将原来的每组观测值(xi1,xi2,xi3,yi)(i=1,2,…,n)变为如下9个观测值(具体展开步骤在2.3节给出)：

2) 考虑回归方程

(4)

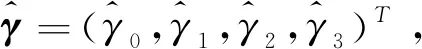
考虑到OR方法在因变量的扩展中不能完全应用原始数据且在使用正交表时容差选取有缺陷，张晓琴等[17]又对yik的产生及容差的取法进行了改进，即OR1方法。具体操作如下：

2) 每个因子xij(j=1,2,3)的容差Δj选取不同的值，取如下形式：

(5)

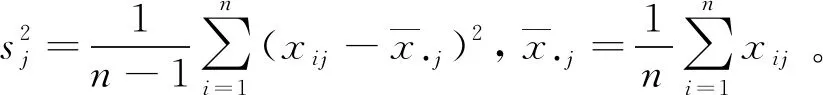
2.2 N-W估计

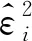
(6)

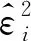
2.3 M-OR1估计

1)对于已有数据(yi,xi1,xi2,xi3),i=1,2,…n,先假设各随机误差项方差相同，由OLS估计得到如下回归模型：

(7)

2)借助正交表

(8)

将原始数据展开，使得每一个样本观测值(xi1,xi2,xi3,yi)(i=1,2,…,n)变为9个观测值：

(9)

其中，每个因子xij(j=1,2,3)的容差Δj按照OR1方法改进后的容差形式(即(5)式)进行选取。

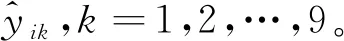
(10)

(11)

2.4 评价指标

方差的估计效果采用以下2个指标进行评价，即方差的平均绝对误差值：

(12)

与因变量的平均绝对预测误差：

(13)

3 随机模拟及实例研究

本节从随机模拟和案例分析两个方面，将M-OR1方法与之前的方法包括HC0，HC4，HC5，OR，OR1方法进行对比分析。

3.1 随机模拟

表1 5个自变量模型的方差平均绝对误差值

从表1可以看出对于自变量的不同取值分布以及样本容量的变化，M-OR1方法的MAEΣ值总小于HC0，HC4，HC5，OR和OR1方法。在样本容量不是很大的时候，M-OR1方法总能给出协方差阵较好的估计。其次，M-OR1方法的MAEy值与先前的方法非常接近。更清晰的对比见图1～图4。

图1 真实方差与基于HC0，HC4，OR与M-OR1估计得出的方差估计值的对比

图2 真实方差与基于上述3种方法及M-OR1估计得出的方差之差的绝对值对比

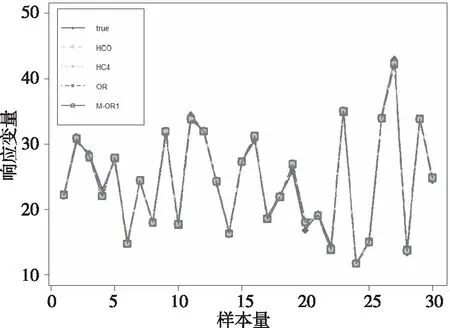
图3 真实因变量与基于HC0，HC4，OR与M-OR1估计的因变量估计值对比

图4 真实因变量与上述3种方法及M-OR1估计的因变量估计值之差的绝对值对比

从表1可以看出，不论模拟实验中自变量的取值分布如何变化，样本容量作何改变，M-OR1方法的MAEΣ值总小于HC0，HC4，HC5，OR和OR1方法。在样本容量不是很大的时候，M-OR1方法总能给出协方差阵较好的估计。其次，M-OR1方法的MAEy值与先前的方法非常接近。

3.2 案例分析

采用本文提出的M-OR1方法对文献[24]中的三大产业的实际案例进行分析。通过异方差检验确定该数据具有异方差性，采用M-OR1方法与HC4和OR1方法对方差进行估计，OR1方法和M-OR1方法均借助正交表L9(34)对观测值进行展开并且采用改进后的容差(即式(5))，本例数据和分析结果见表3。

表3 实例分析数据及比较结果

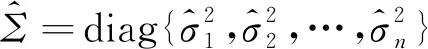
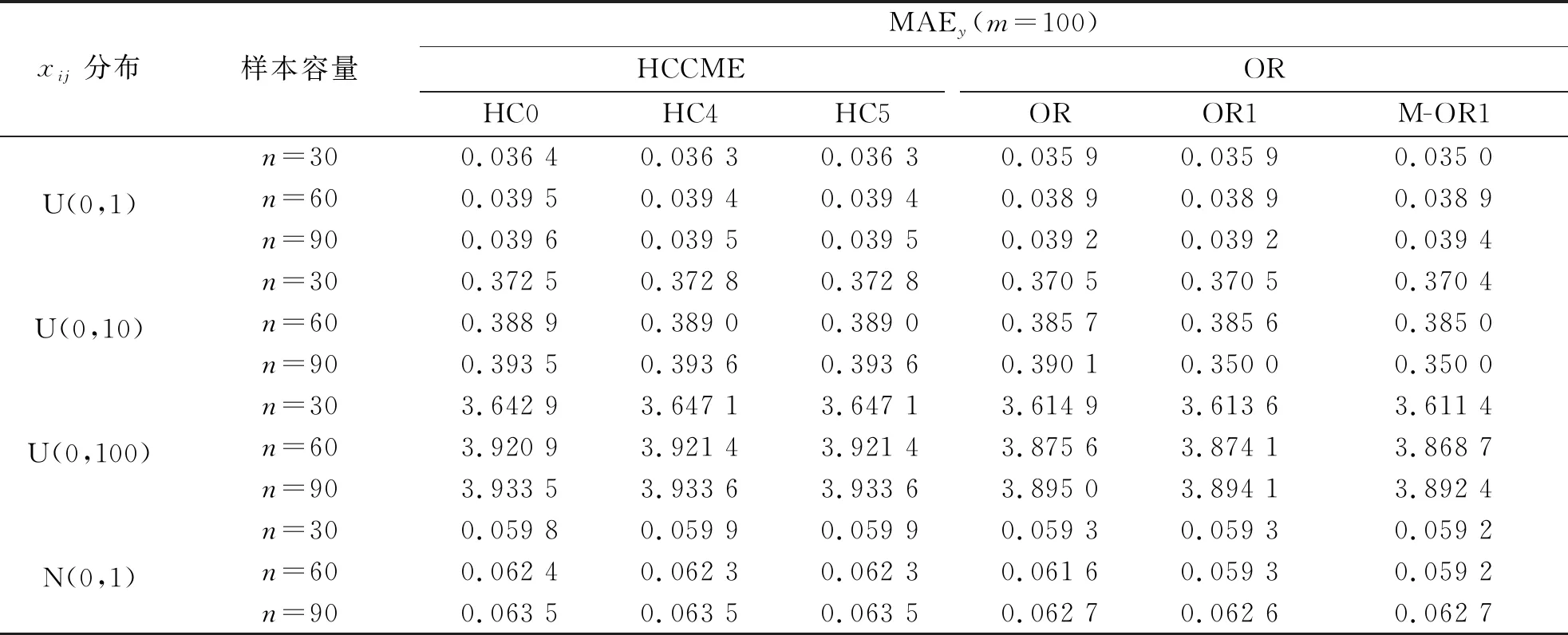
表2 5个自变量模型的因变量平均绝对误差值

续表3

4 结论

基于正交表估计协方差阵的方法是近年来提出的新方法。在异方差形式未知的情况下，本文在已有的正交表方法中引入了非参数估计，即在利用正交表扩展后的模型中，用非参数的方法对各项方差给出了估计，在随机模拟中，通过样本容量以及自变量分布的变化说明了该方法的优越性，同时实例分析也表明，本文所提出的方法比原有的估计方法对于协方差阵的估计更加准确。不过，基于正交表进行异方差估计的相关方法在自变量的维数较低时比较有效，还可以对多个自变量的情况进行进一步的讨论。