矩阵最小奇异值的下界

廖 平

(四川职业技术学院，四川 遂宁 629000)

0 引言

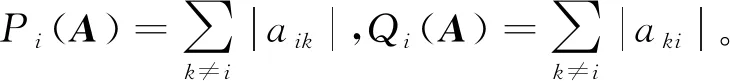
(1)

(2)

文[4]利用G-函数与矩阵非奇异的关系推广了文献[3]的结果，得到如下估计：

设A为n阶复矩阵，f=为G-函数，则

(3)

但显然不论(2)或(3)，对Reaii≤0,i=1,2,…,n所得下界都是平凡的。与此同时，其它的一些特征值包含定理也被应用于最小奇异值估计中，得到一些其他结果[5-9]，在文献[10]中还利用矩阵的行列式得到最小奇异值的一些新下界，然而对一般高阶矩阵而言，行列式的计算也极为不易。

本文在现有结果的基础上，结合奇异值的自身特点，首先得到矩阵最小奇异值下界的一个新估计，然后利用该估计进一步改进了文献[4]和[7]的结果。

1 主要结果

首先，我们给出文中用到的一些定义和引理。

定义[4]f=称为一个G-函数，如果0≤fi(A)<∞,i=1,2,…,n，fi(A)仅依赖于A的非对角元的模，且对于任意满足|aii|>fi(A),i=1,2,…,n的矩阵A，A都非奇异。

根据G-函数的定义，我们可以得到关于矩阵半正定或半负定的一个判定准则。

引理1 设A为n阶Hermite矩阵，为G-函数，

(a)若aii-fi(A)≥0，i=1,…,n，则A半正定；

(b)若aii+fi(A)≤0，i=1,…,n，则A半负定。

证明由G-函数的定义，A的任意特征值包含在以下集合的并集中：

Ωi={λ∈C:|λ-aii|≤fi(A)}，i=1,2,…,n。

设矩阵A的特征值按大小顺序依次为λ1(A)≥λ2(A)≥…≥λn(A)。当所有对角元aii满足aii-fi(A)≥0时，λn(A)≥aii-fi(A)≥0，从而半正定。当所有对角元aii满足aii+fi(A)≤0时，λ1(A)≤aii+fi(A)≤0，从而半负定。

下面我们给出关于矩阵最小奇异值下界的一些估计结果。

证明对任意实数t，令M=A-tI，则MM*=AA*-t(A+A*)+t2I，从而AA*=MM*+t(A+A*)-t2I，又因x为σn(A)对应右单位特征向量且MM*半正定，从而有

由引理2我们立即得到如下定理

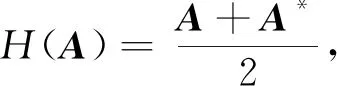
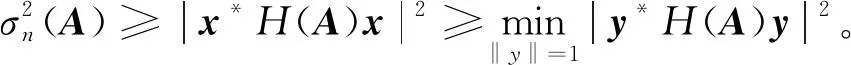
推论1 设A为n阶矩阵，若H(A)半正定或半负定，设H(A)的特征值按绝对值大小依次为|λ1(H)|≥|λ2(H)|≥…≥|λn(H)|≥0，则σn(A)≥|λn(H(A))|。

同时，也可以利用对角矩阵D=diag(eiθ1,eiθ2,…,eiθn)将矩阵A的对角元素全变为非负，且不改变其奇异值，故又可得如下结果。

证明由DA与A有相同奇异值，对DA用定理1即得。

若H(DA)半正定或半负定，同样可得如下推论。

推论2 设A为n阶矩阵，D=diag(eiθ1,eiθ2,…,eiθn)使DA的对角元为|aii|，i=1,2,…,n。若H(DA)半正定或半负定，且H(DA)的特征值按绝对值大小依次为|λ1(H(DA))|≥|λ2(H(DA))|≥…≥|λn(H(DA))|≥0，则σn(A)≥|λn(H(DA))|。

下面结合G-函数的定义和上文的结论，我们得到只依赖矩阵元素的最小奇异值下界估计。

定理3 设A为n阶矩阵，为一个G-函数，

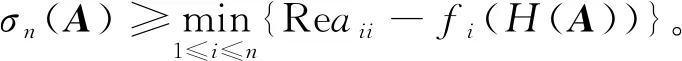
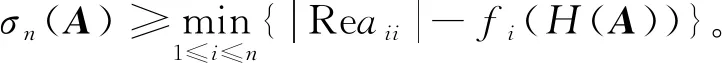
注1 当Reaii≥0时(i=1,2,…,n)，由推论3之(a)即得文献[4]的结论，但对Reaii≤0的情况，文[4]得到的下界是平凡的，但本文定理3则可能得到非负的下界。

类似地，由推论2又可得如下结果

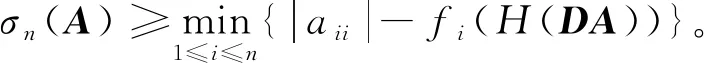
注2 利用矩阵D=diag(eiθ1,eiθ2,…,eiθn)使DA的对角元为|aii|后再进行估计不一定比直接对矩阵A进行估计效果好。比如考虑如下矩阵

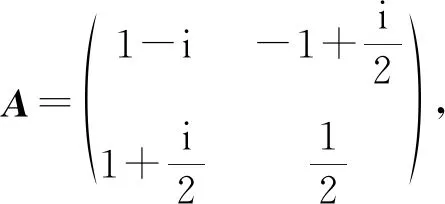
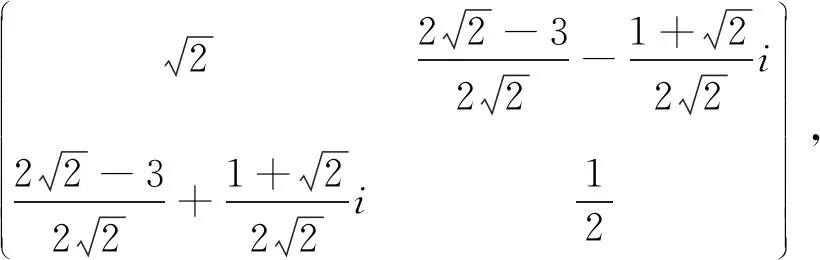
下面我们给出矩阵半正定或半负定的另一判定，从而给出奇异值下界的另一改进估计。

引理3 设A为n阶Hermite矩阵，

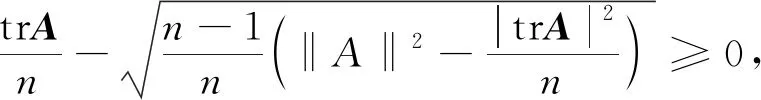
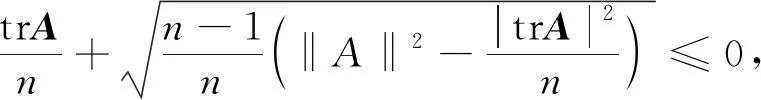
证明由文[5]知，矩阵A的任意特征值λ包含在以下区域内

设其特征值按大小顺序依次为λ1(A)≥λ2(A)≥…≥λn(A)。

由此，我们又可得以下关于最小奇异值的下界估计

定理4 设A为n阶矩阵，则

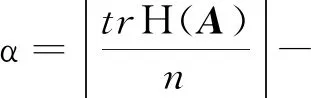
注3 显然定理4改进了文献[7]的相关结论。

[34]CHEN M,CHANG L,ZHANG J,et al.Global nitrogen input on wetland ecosystem:the driving mechanism of soil labile carbon and nitrogen on greenhouse gas emissions[J].Environmental Science and Ecotechnology,2020,4:26-38.

[35]TONG X,WANG K,BRANDT M,et al.Assessing future vegetation trends and restoration prospects in the Karst regions of southwest China[J].Remote Sensing,2016,8(5):357-374.

[36]HUNGATE B A,DUVAL B D,DIJKSTRA P,et al.Nitrogen inputs and losses in response to chronic CO2exposure in a subtropical oak woodland[J].Biogeosciences,2014,11(12):3323-3337.

[37]SHAHZAD H,IQBAL M,JAVED A,et al.Nitrification dynamics in soil due to variation in CO2level[J].Russian Journal of Agricultural and Socio-Economic Sciences,2015,38(2):15-19.

[38]WEHRLE R,WELP G,PATZOLD S.Total and hot-water extractable organic carbon and nitrogen in organic soil amendments:their prediction using portable mid-infrared spectroscopy with support vector machines[J].Agronomy,2021,11(4):659-676.

[39]CHRISTENSEN S,SIMKINS S,TIEDJE J M.Temporal patterns of soil denitrification:their stability and causes[J].Soil Science Society of America Journal,1990,54(6):1614-1618.

[40]GOODALE C L,FREDRIKSEN G,WEISS M S,et al.Soil processes drive seasonal variation in retention of15N tracers in a deciduous forest catchment[J].Ecology,2015,96(10):2653-2668.

[41]KRAL J,VACEK S,VACEK Z,et al.Structure,development and health status of spruce forests affected by air pollution in the western Krkonoe Mts.in 1979—2014[J].Forestry Journal,2015,61(3):175-187.