交错磁极混合励磁电机漏磁系数计算与分析

吴胜男，王玉坤，佟文明，李世奇

(1.沈阳工业大学 电气工程学院，辽宁 沈阳 110870； 2.沈阳工业大学 国家稀土永磁电机工程技术研究中心，辽宁 沈阳 110870)

0 引 言

混合励磁电机是永磁电机和电励磁电机的结合，具有功率密度高和气隙磁场调节灵活的特点。应用于风力发电机当中，在转速变化时调节电励磁电流的大小和方向可以稳定输出电压。本文所研究的交错磁极轴向/径向磁路混合励磁同步发电机最早由日本学者 T.Mizuno博士提出，该电机将电励磁绕组居中放置于定子圆周上，转子采用交错磁极结构，通过控制电励磁绕组的电流大小和方向，可以灵活地调节和控制电机的气隙磁场大小[1-2]。后来，美国学者T.A.Lipo对该电机进行了深入的研究，提出轴向磁场盘式结构的混合励磁电机，其工作原理和日本学者T.Mizuno博士提出的结构相似。文献[3-4]采用三维有限元的方法分析了一台功率为3 kW的交错磁极混合励磁电机的电磁场，并探究了不同电励磁电流下的磁场分布和反电势波形。沈阳工业大学特种电机研究所的张宏杰和金万兵也对日本学者的这一电机结构进行了研究，并在此基础上提出增加永磁电机部分体份额的方案，研究了电压调整率和正弦畸变率，但都未对该类电机的空载漏磁系数进行深入研究[5-6]。文献[7]采用三维电磁场有限元分析了一台100 kW增加永磁体份额的交错磁极混合励磁电机在不同电励磁条件下的三维磁场分布。文献[8]采用三维有限元分析了一台混合励磁爪极同步发电机的漏磁系数随电机尺寸参数变化的规律。文献[9]采用三维有限元修正等效磁路法的等效磁阻方法对一台永磁外转子发电机的漏磁系数进行计算。文献[10]采用解析计算的方法对表贴式轴向磁通永磁同步电机的齿顶漏磁和漏磁系数进行计算。文献[11]采用等效磁路的方法对一台轴向磁通永磁同步电机的气隙漏磁进行计算。文献[12]研究了常规永磁同步径向电机在近极槽配合下的齿顶漏磁变化规律。文献[13]采用等效磁路法研究了一台内置式永磁同步电机的漏磁系数。文献[14-15]针对表贴式永磁同步电机的漏磁导进行了解析计算。

本文提出一种采用二维电磁场有限元和三维电磁场有限元相结合的混合计算方法，并针对一台额定功率10 kW的增加永磁体份额的交错磁极混合励磁恒压风力发电机样机的漏磁系数进行计算。通过分析增加永磁体份额的交错磁极混合励磁电机发电机的结构特点，将该电机分为永磁电机部分和混合励磁电机部分。在永磁电机部分采用二维有限元进行计算，在混合励磁部分采用三维电磁场进行计算，避免整体采用三维有限元计算对计算机资源和计算时间的巨大消耗，也可以探究永磁电机部分和混合励磁电机设计部分的漏磁差异和规律。最后，将有限元分析得到的漏磁系数与实验得出的漏磁系数进行对照，验证有限元计算结果的准确性，对该类电机的设计提供一定的理论参考。

1 交错磁极混合励磁电机结构

本文研究的混合励磁电机磁路既有径向磁路又有轴向磁路，磁通路径复杂。图1为一个8极9槽单元电机结构。从定子上看，最外层是导磁背轭，其目的是为混合励磁部分提供轴向导磁路径。电枢绕组采用的是集中绕组，缠绕在模块化的定子上，最后进行组装。直流励磁绕组居中放置在定子圆周上，针对混合励磁部分磁场进行调节。图2为电机转子结构，转子沿轴向分成了3段，依次为永磁电机部分、混合励磁电机部分、永磁电机部分。永磁体采用矩形结构，嵌套在叠压的硅钢片极靴中，采用该结构的永磁体加工成本较低。混合励磁部分的转子采用交错磁极结构。

2 混合励磁电机漏磁分析

2.1 永磁电机部分漏磁分析

该混合励磁电机的永磁电机部分磁通仅沿径向分布，故可采用二维电磁场有限元进行分析。由于近极槽电机的漏磁规律呈现周期分布的特点，重复的周期数是定子槽数Q与极对数2p的最大公约数(greatest common divisor,GCD)。对于本文27槽24极的电机，其重复周期为3,每个重复单元为8极9槽。针对该单元电机进行二维电磁场分析，结果如图3所示，展示了该电机永磁电机部分一个单元电机的磁力线走向，不同于整数槽电机每极下的磁通路径相同。在近极槽数的8极9槽极槽配合下，每一极对应的磁通路径都不尽相同，存在大量齿顶漏磁。不同定转子相对位置的齿顶漏磁如图4所示，展示了两种典型的定转子相对位置，图4(a)为典型的齿顶漏磁情况，磁力线从永磁体出发后，虽经过气隙，但经由定子齿直接回到另一极永磁体，未与电枢绕组交链，因此也归属于漏磁通。 图4(b)为典型的定子齿尖处的齿顶漏磁路径，由于齿尖漏磁要经过槽口处磁阻较大的空气，齿尖处的齿顶漏磁占比非常小。

为更好地展示每个定子齿上的磁通分布，采用仿真后处理中的场计算器工具，对磁密进行线积分的方法进行准确计算，并研究一个单元电机下的各部分磁通分布情况，如图5所示。在单元电机为8极9槽时，9个定子齿上与电枢绕组交链的磁通为主磁通，其中定子齿的序号在图3中进行了标注。由仿真数据可知，一个周期内的9个定子齿主磁通量呈对称分布，定子齿上的磁通量先减小后增加。其中第5个定子齿的磁通量接近于0，这是由于该定子齿和永磁体的相对位置处在图4(a)所示的情况，此时发生了严重的齿顶漏磁，该齿上不存在主磁通。

在单元电机为8极9槽的分数槽集中绕组下，由于定子齿与永磁体的相对位置不同，两个定子齿之间的齿顶漏磁也随之变化。图6为8个定子齿间的齿顶漏磁仿真结果，齿顶间的漏磁通先增大后减少。在第4个齿间的齿顶漏磁达到最大，此时对应第5个定子齿上的主磁通接近于0。

由于采用8极9槽的近极槽配合，每极磁通的情况按一定规律变化，因此，以一个单元电机的磁通量总和进行漏磁计算更为简便和准确，参照漏磁系数的定义，该交错磁极混合励磁同步电机的永磁部分漏磁系数可以表示为单元电机下永磁体总磁通与电枢绕组相交链总磁通的比值，表达式为

(1)

式中：Φr(i)为永磁电机部分第i个永磁体提供的磁通量；Φam(j)为永磁电机部分第j个定子齿上的有效磁通量。

该交错磁极混合励磁同步电机单元电机下永磁部分主磁通总量为0.127 7 Wb, 永磁体磁通总量为0.228 6 Wb。漏磁系数采用式(1)进行计算，永磁电机部分的漏磁系数为1.79，其中齿顶漏磁占总漏磁的比例可达27.5%，齿顶漏磁占据了较大比例，降低了永磁体的利用率。

2.2 混合励磁部分漏磁分析

该电机的混合励磁部分磁通呈现三维特性，二维电磁场仿真已经无法求解，因此针对混合励磁部分的漏磁分析将采用三维电磁场进行研究。首先，搭建混合励磁电机部分的三维模型，进行模型的前处理和剖分，剖分示意图如图7所示。

针对求解后的结果进行后处理分析。仅永磁体作用时的单元电机的磁密分布云图如图8所示，其中永磁N极和永磁S极构成主磁路，因此，永磁极处的定子和转子轭部的磁密较铁心极处高。永磁极上极靴两端隔磁桥处的磁通为永磁体的自身漏磁，隔磁桥处较为饱和可以限制漏磁。铁心极仅与圆周方向相邻的永磁极构成部分漏磁通，在磁密云图中进行局部放大展示，铁心极在圆周方向上的两端略有磁密，而内部基本无磁密。

图9为半对极下的磁密矢量云图，较为清楚地看出仅永磁体作用下的磁通路径，主磁通路径为永磁N极-定子齿-定子轭-定子背轭-定子轭-定子齿-永磁S极-转子轭。定子背轭具有明显的轴向磁通特性，因此，该电机的背轭必须采用实心结构以提供轴向磁通路径。

对混合励磁部分的漏磁进行分析，对仿真结果进行后处理。以8极9槽单元电机为一个重复周期，对所研究的主磁通和漏磁通的磁密进行面积分处理。其中定子齿上的主磁通分布结果如图10所示。定子齿序号对应图8中的序号，考虑到轴向前后的定子齿磁通并不相同，因此分别计算轴向前后定子齿的磁通量。在图8的定转子相对位置下，第一个永磁极和定子1号齿正对，此时主磁通为轴向前半部分定子齿1号流向轴向后半段定子齿2号。而从第2～7个永磁极开始，永磁极将对应两个定子齿，第8个永磁极再次对应一个定子齿，在一个单元电机内形成交错对称分布，具体分布结果如图10所示。

混合励磁电机部分漏磁系数仍为永磁体总磁通与定子齿上和电枢绕组相交链的总磁通比值。与永磁电机部分不同的是，此时轴向前后两个定子齿的磁通量已经不再一致。此时的漏磁系数为

(2)

其中：永磁体总磁通量为0.030 844 Wb；主磁通为0.024 38 Wb；漏磁系数为1.265。相较于永磁电机部分，混合励磁电机部分的齿尖漏磁较小，漏磁系数降低，永磁体利用率得到提升。

2.3 混合励磁电机整体漏磁系数研究

上文将一台增加永磁电机部分配比型混合励磁电机分成了永磁电机部分和混合励磁电机部分。针对各自磁路特点分别采用二维有限元和三维有限元对磁通部分和漏磁系数进行计算分析，避免了整机全部采用三维有限元分析而忽略了内部两部分不同漏磁特性的问题，并解决了整体采用三维电磁场计算时带来的耗时严重问题。而对整机的漏磁系数进行分析时，需要将两部分的永磁磁通和主磁通分别求和，整机的漏磁系数表达式为

(3)

以一台10 kW交错磁极混合励磁风力发电机样机为例，永磁电机部分轴向长度520 mm，混合励磁部分轴向长度140 mm，计算其漏磁系数，比较整体采用三维有限元方法和二维三维混合有限元方法的计算耗时，具体数据如表1所示。处理器采用Intel(R) Core(TM) i7-10700。

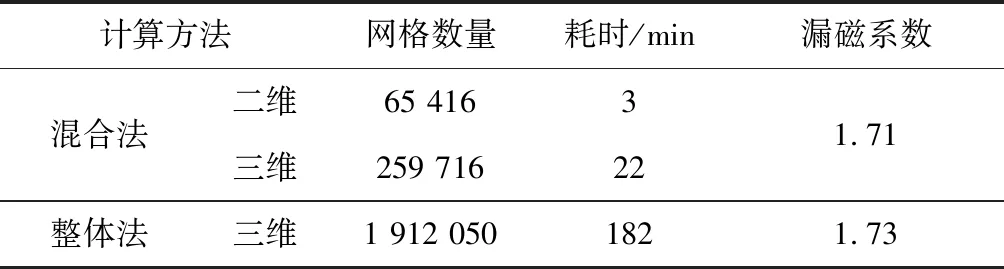
表1 两种漏磁系数计算方法比较

对于漏磁系数的计算，分别采用本文提出的二维三维混合有限元与整体三维有限元的方法进行计算，从漏磁系数的计算结果来看，两种方法的计算结果接近，误差仅有1.9%。但本文采用的混合有限元方法网格数量比采用整体三维有限元法减少了98.3%，计算耗时比整体有限元法减少了86.3%。因此，该方法能够在保证精度的前提下，极大地压缩仿真计算时间，节约硬件资源，提升计算效率。

由于本文采用的混合有限元法将该混合励磁电机在轴向上分成了永磁电机和混合励磁电机两部分，分别对主磁通和永磁磁通进行计算。这种计算方法可以仅通过一次计算便得到永磁电机部分和混合励磁电机部分不同轴向长度配比时的漏磁系数，解决了整体三维有限元法无法分离出永磁电机部分磁通和混合励磁电机部分磁通，不同配比方案时需要反复进行耗时计算的问题。下面针对不同配比问题采用混合有限元法进行计算，该方法可以一次计算得到不同配比下的漏磁系数。在总轴向长度不变的基础上，调整两部分长度，研究漏磁系数变化规律，如表2所示。可以看出，随着混合励磁电机部分的占比增大，漏磁系数随之减少，永磁体利用率提高。全部为混合励磁部分时的漏磁系数达到最小，但此时该电机的功率密度将大幅减少，因此，在选择配比时需要综合考虑，参照实际需求对其进行选取。

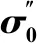
表2 永磁电机部分与混合励磁电机部分配比对漏磁 系数影响

3 实验验证

由于样机的空载漏磁系数无法通过实验直接测量，因此通过实验测量空载反电势并与有限元法得到的空载反电势对照，实验结果如表3所示。若实验测量与有限元法得到的空载反电势接近，可以验证有限元法仿真的正确性，进而认为漏磁系数计算准确。实验装置如图11所示，采用直流电机作为原动机，配合减速齿轮箱拖动样机到额定转速，测试其空载反电势。

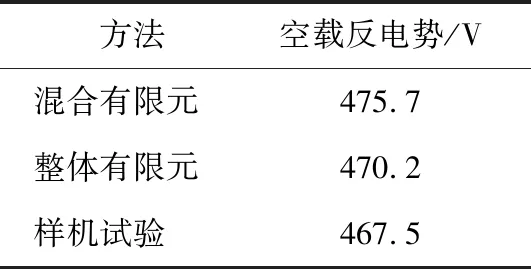
表3 仿真与实验得到的空载反电势

实验结果表明，经过实验实测的空载反电势为467.5 V，与整体有限元法和混合有限元法结果相接近，误差在1.16%。本文提出的混合有限元法计算值与实验值误差在1.75%，误差较小，可以认为混合有限元法与实际模型相符，漏磁系数与实际一致。

4 结 论

本文提出一种将交错磁极混合励磁电机沿轴向分为永磁电机和混合励磁电机两部分的方式对漏磁进行分析，并采用二维和三维有限元混合计算的方法分别对两部分磁通量进行分析并计算。该方法既可以研究两部分不同的漏磁规律又解决了整体采用三维有限元的耗时严重问题。最后，采用混合有限元法计算永磁电机部分和混合励磁电机部分不同配比情况下的漏磁系数变化情况。将整体有限元法、混合有限元法和实验结果对照，结果非常接近，证明了该混合有限元法计算的准确性。整个研究过程得出以下结论：

1)针对交错磁极混合励磁电机采用三维电磁场求解耗时严重的问题，本文提出采用二维和三维有限元混合计算的方法。在计算精度只相差1.9%的前提下，节约了86.3%的计算时间，该方法具有优越性。

2)通过混合计算法对磁通分布进行研究。在主磁通方面，该电机的永磁电机部分呈现周期分布，混合励磁电机部分则呈现交错对称分布。在漏磁方面，混合励磁部分的漏磁系数比永磁电机部分的漏磁系数小。

3)随着该电机的混合励磁电机部分与永磁电机部分的轴向长度配比提升，漏磁系数可降低。因此，在满足功率密度的前提下，可以通过增加混合励磁电机部分的占比来提高永磁体的利用率。