基于振动特征值的动车组齿轮箱故障检测

林新海 ， 董 婷 ， 许 行

（中车戚墅堰机车车辆工艺研究所有限公司，江苏 常州 213001）

0 引言

齿轮箱是动车组转向架的关键部件，其主要作用是将牵引电机的转速扭矩转化为轮对走行的转速扭矩。齿轮箱的加工制造及安装误差，以及服役过程中的疲劳、磨损、腐蚀等，都会导致齿轮箱轴承产生振动，直接影响整个传动系统的转动精度与平稳性，甚至会引发严重的安全事故。由于齿轮箱的性能和可靠性与动车组的安全运行直接相关，因此，通过试验方法检测齿轮箱性能及判定其健康状态，是一项至关重要的研究内容[1-2]。

振动是一切运动机械以及承受动态载荷的工程结构所具有的运动现象。振动信号中包含着机械及结构的内在特性和运行状况信息。经验表明，齿轮箱由一种或多种上述情况引起的故障损坏可通过振动水平的提高而显现出来，通过振动信号的采集与处理来研究齿轮箱的状态是一种非常有效的检测、诊断方法[3-7]。齿轮箱振动的分析方法主要包括时域、频域和时频域3 类。丁保华等[8]针对齿轮箱故障振动信号传统的时域、频域分析方法，列举了一些不同故障所应用的分析方法，并介绍了一些基于非平稳信号处理的方法特点及应用，指出了齿轮箱故障诊断的发展趋势。候有忠[9]对CRH2 型动车组齿轮箱的跑合试验振动数据进行了分析，通过不同工况下的频谱、峭度、偏度等指标，对比分析了齿轮箱的运行状态。赵春等[10]对动车组齿轮箱在振动分析的基础上进行了模态试验和线路跟踪测试，通过频谱分析发现振动主频介于500～600 Hz 之间，研究确定齿轮箱的异常振动来源于轮轨的高频激扰所引起的结构共振。

目前动车组齿轮箱的型式试验主要是依据TB/T 3134—2013 规定的振动速度有效值进行测试评价[11]。为进一步提升齿轮箱故障的监测与评估，本研究通过提取动车组齿轮箱试验中振动信号的特征值，将不同运行速度、不同故障模式下的各类特征值与正常状态的齿轮箱振动特征值进行对比，筛选出具有良好敏感性的特征值，为动车组齿轮箱故障检测与诊断提供理论与技术基础。

1 齿轮箱振动特征值

当机器零件类型不同、具体故障不同以及损伤程度不同时，其损伤特征的类型各不相同。因此，基于不同的特征值，就可能定位有缺陷的零件（如轴承或齿轮）和隔离零件中的具体故障，并确定其损伤程度。

时域分析是根据信号的时间历程记录波形，分析信号的组成和特征量，从而在时间坐标轴上显示出振动信息的方法。根据齿轮箱的振动特点，以时域振动信号的统计量作为损伤（或故障）的敏感性特征，通过在齿轮箱表面安装的振动加速度传感器获取时域信号。当齿轮箱发生故障时，信号本身会出现能量的变化，对于一组离散测试信号[X1,X2,…,Xn]，可用不同统计量捕获原始信号的不同特性[12-13]。

1）有效值XRMS描述振动信号的能量，是机械故障诊断系统中用于判断是否存在故障的重要指标，它反应振动对时间变化的过程。

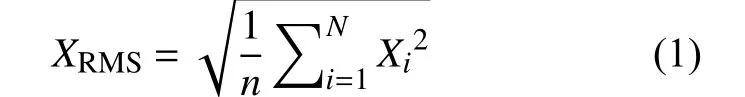
2）峰值Xp是描述波形与零线的最大偏离度，是在一个周期中的最大瞬时值。产品的结构强度性破坏直接与峰值有关。

3）标准差σ度量时间序列幅值关于均值的离散程度。当零件从初始损伤状态发展到下一更高程度损伤时，标准差会显著增加。

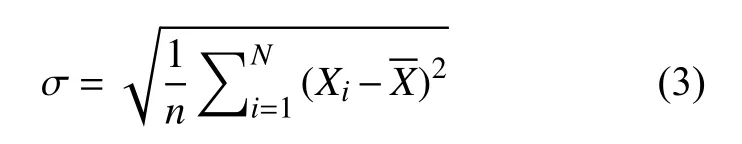
4）偏度Cw反映振动信号的非对称性。当机械结构存在某一方向的摩擦或者碰撞时，会造成振动波形的不对称，偏度会增大。

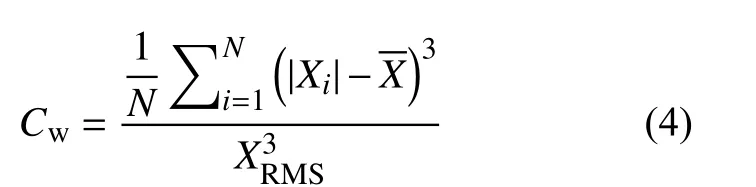
5）峭度Cp反映波形的平缓程度，用于描述变量的分布。在高斯振动下的峭度为3。在峭度大于3 的随机振动中，会有一部分极大值超过3 倍标准差，引起产品的疲劳和损伤。

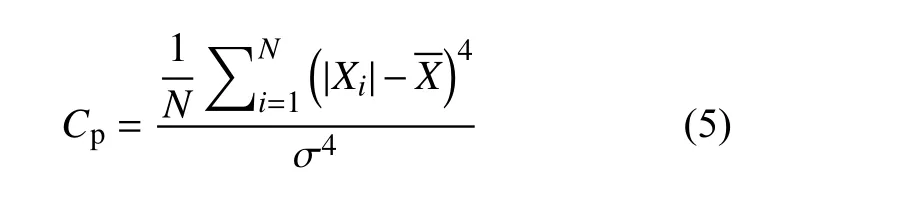
6）波形系数K用于检测机械设备的磨损情况。若波形系数指标增大，说明有效值XRMS比平均值X增大快，即磨损导致的间隙增大。

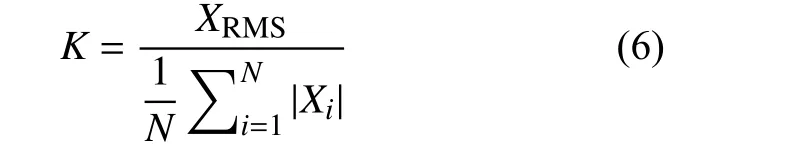
7）峰值系数C是和波形有关的无因次量，是信号峰值与有效值（RMS）的比值，代表的是峰值在波形中的极端程度。

8）冲击系数I是信号峰值与整流平均值（绝对值的平均值）的比值。冲击系数和峰值系数的区别在分母上，由于对于同一组数据整流平均值小于有效值，所以冲击系数大于峰值系数。

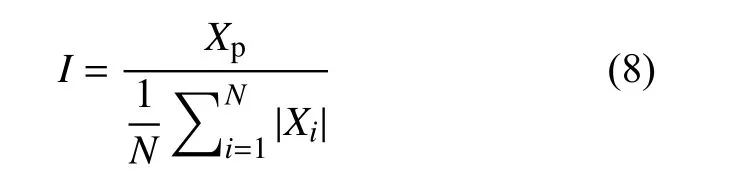
2 试验方法

齿轮箱空载试验如图1 所示。试验对象为动车组齿轮箱，齿轮箱速比为2.379，输入端与输出端均为圆锥滚子轴承。试验最高转速可达6070 r/min。在齿轮箱输入端轴承座安装一个三向加速度传感器，采样率为10 240 Hz，高于齿轮的一般工作频率（0～2000 Hz）。在测试期间，通过驱动电机驱动齿轮箱运转，在500～6070 r/min 选择8 种转速以模拟动车组齿轮箱在运行期间经历的各种转速状态，正反转分别运行。

图1 齿轮箱空载试验台Fig.1 No-load test bed for gearboxes

被试齿轮箱分别安装正常轴承与故障模拟轴承。故障模拟轴承是对主动齿轮的轴承进行人为破坏。图2 为滚道裂纹故障轴承。

图2 故障模拟轴承Fig.2 Fault simulation bearing

3 试验结果

为了对比不同轴承故障模式下振动特征值的变化规律，分别截取齿轮箱在不同转速稳态下的加速度信号进行分析。时域信号特征值分为有量纲特征值和无量纲特征值两类，其中，有量纲特征值包括有效值XRMS、峰值Xp、标准差σ等，无量纲特征值包括偏度Cw、峭度Cp、波形系数K、峰值系数C和冲击系数I等。因此，按照振动时域信号特征值分类进行试验数据对比。

3.1 有量纲特征值对比分析

振动有量纲特征值的数值大小常因外界试验条件的变化而变化，从有量纲特征值中选取振动加速度有效值进行对比分析。图3、图4 分别为不同转速下无故障轴承和滚道裂纹轴承的齿轮箱振动加速度有效值变化曲线，其中PWX、PWY、PWZ分别表示轴承振动的3 个方向（下同）。通过对比可知，随着转速增加，3 个方向的振动加速度有效值随转速变化明显；在相同转速下，故障轴承的振动加速度有效值相对于无故障轴承都有一定的增大，且转速越高，增幅越明显。

图3 无故障轴承振动加速度有效值曲线Fig.3 RMS curves of vibration acceleration of vault-free bearing

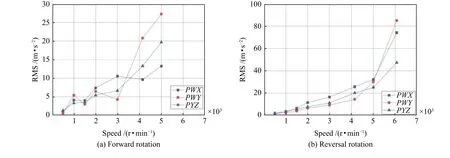
图4 滚道裂纹轴承振动加速度有效值曲线Fig.4 RMS curves of vibration acceleration of raceway cracking bearing

3.2 无量纲特征值对比分析

无量纲特征能够排除工作条件的扰动影响，因此，不同运行速度下的特征值可以直接对比。从无量纲特征值中选取振动加速度峭度为典型特征值进行分析。图5、图6 分别为不同转速下无故障轴承和滚道裂纹轴承的齿轮箱振动加速度峭度变化曲线。从图中可以看出，在同一轴承状态下，峭度特征值不随运行转速的变化而变化；但对于不同的轴承来说，轴承损坏越严重，峭度越大越离散，这也说明试验运行过程中具有较大的振动冲击。

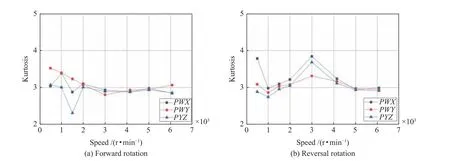
图5 无故障轴承振动加速度峭度曲线Fig.5 Kurtosis curves of vibration acceleration of fault-free bearing

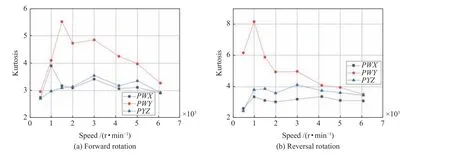
图6 滚道裂纹轴承振动加速度峭度曲线Fig.6 Kurtosis curves of vibration acceleration of raceway cracking bearing

3.3 敏感度分析

为分析7 个特征值指标在各种状态下的评价敏感性，将正常轴承在各工况下的特征值计为X1，损坏轴承在各工况的特征值计为X2，X2与X1相除所得敏感系数计为Z。Z越大，说明该特征值分类距离感越强，特征值指标越敏感。

以等比系数1.25 来区分各特征值敏感度，分为4 级：1）Z＜1.25，代表此特征值不敏感；2）1.25≤Z≤1.56，代表轻微敏感；3）1.56＜Z≤1.95，代表中度敏感；4）Z＞1.95，代表高度敏感。各特征值在所有转速工况下各级敏感性的占比见图7。

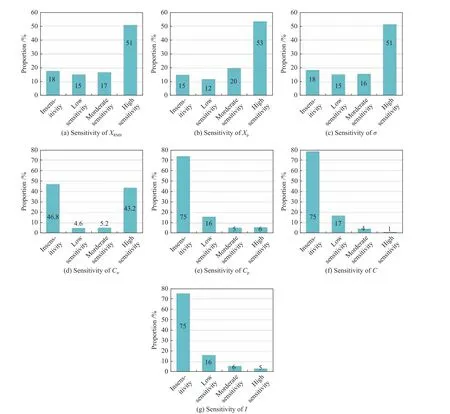
图7 振动特征值敏感度分布Fig.7 Vibration eigenvalue sensitivity distribution

从图7 可知，有量纲特征值的敏感度整体上高于无量纲特征值的敏感度。特征值指标按其敏感度从高到底的排序为峰值、有效值、标准差、偏度、峭度、冲击系数、峰值系数。

4 结论

1）动车组齿轮箱不同的故障模式将直接影响振动特征值。

2）有量纲振动特征值受运行转速影响较明显，运行转速越高，相应特征值变化越明显。

3）无量纲振动特征值受轴承故障模拟形式影响较大，与运行转速关系较小。

4）通过对比故障状态下振动特征值的敏感度，有量纲特征值比无量纲特征值对故障更加敏感。