一类时滞项含区间系数的2-D离散系统的稳定性*
2010-01-08高存臣张筱蓉
高存臣,张筱蓉
(中国海洋大学数学科学学院,山东青岛266100)
一类时滞项含区间系数的2-D离散系统的稳定性*
高存臣,张筱蓉
研究时滞项含区间系数的2-D离散系统的稳定性问题,应用不等式技术,通过对区间系数分3种情况讨论,得到了一类时滞项含区间系数的2-D离散系统渐近稳定的一个充分条件。所给的数值例子说明了该方法的有效性。
区间系数;时滞;2-D离散系统;稳定性
2-D(二维)离散系统自Roesser[1]于1974年创建基本理论以来,已有30多年了,由于它特有的深刻工程物理背景以及模型的工程实现及一些工程实际问题中的应用,使它成为控制系统理论的一个具有强大生命力和发展前景的学科分支,它在数字滤波器、图像加强、图像清晰化、信号处理等领域的广泛应用,己引起了许多学者的兴趣,目前已有了一些结论[1-4],但在具有时间滞后(简称时滞)的2-D离散系统中还存在着大量亟待解决的问题。实际的工程应用中存在各种各样的不确定性,二维系统具有区间系数的情况也是实际工程当中会遇到的。文献[1]用不等式分析方法给出了具有时滞的2-D离散系统稳定的充分条件。在一维离散系统中,具有区间系数的情况可以通过构造辅助系统得到系统稳定互相蕴涵的一些条件[5-6]。而对具有区间系数的时滞2-D离散系统的稳定性研究还未见到报道。本文在前人的基础上,采用不等式技术,对具有区间系数的时滞2-D离散系统的稳定性问题进行了分析,通过对区间系数分3种情况的讨论,最后得到了时滞项具有区间系数的2-D离散系统渐近稳定的一个充分条件。
(中国海洋大学数学科学学院,山东青岛266100)
1 问题的提出
考虑如下的时滞项含区间系数的2-D离散系统

其中1≤i≤n;j>0,且i;j∈N,时滞σ为非负常数,都是实数序列。而
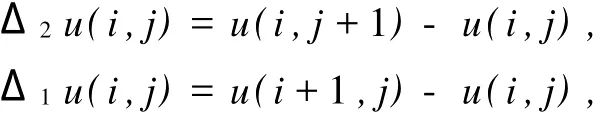
对(1)考虑相应的边界条件
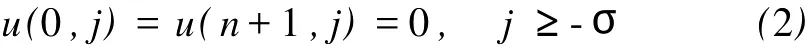
及初始条件

2 有关引理
为了对滞后项含区间系数的2-D离散系统的稳定性进行分析,先给出已有的关于时滞2-D离散系统稳定性的有关引理。
考虑如下时滞2-D离散系统
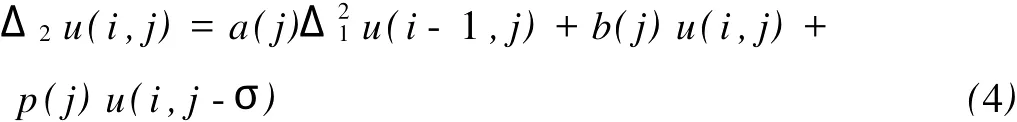
引理1[1][时滞2-D离散系统的渐近稳定性定理]若对j≥0,有a(j)>0,且存在正数δ,η使得

与

成立,则存在常数M>0和ζ>1,使得系统(4)(2)(3)的所有解u(i,j)均满足
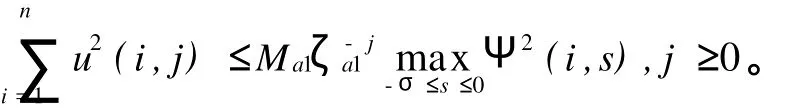
3 对区间系数的讨论
对具有区间系数的情况,因c (j)≤c(j)≤?c(j),可
取
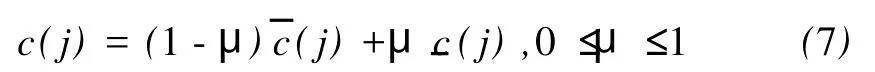
如果对j≥0,有a(j)>0,存在正数δ?,η?,使得

成立,且存在正数δ,η,使得
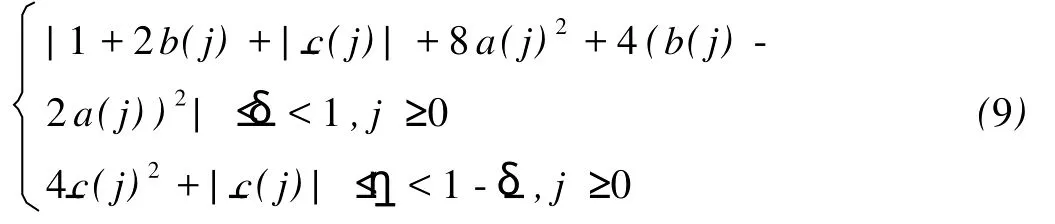
以下分3种情况讨论。
显然有|?c(j)|=?c(j),|c (j)|=c(j),根据(8)式则有

同样根据(9)式有

由(7)式易知c(j)>0,将(10)中第一式两边同时乘以1-μ,(11)中第一式两边同时乘以μ,然后相加,可以得到,

于是可取δ=(1-μ)δ?+μ δ,因为0<δ?<1,0<δ<1,易知0<δ<1。则(12)式可以化为
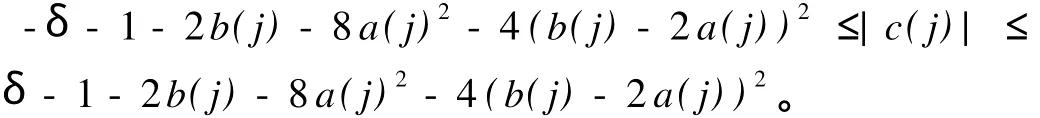
通过移项整理得
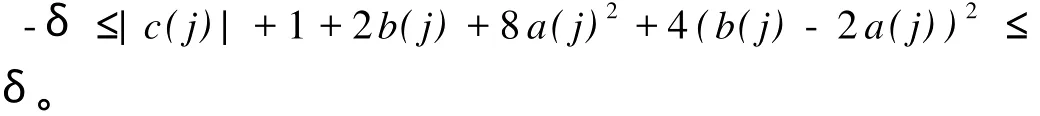
也即
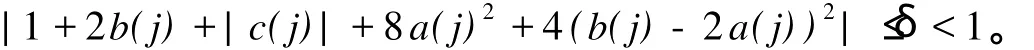
将(10)中第二式两边同时乘以1-μ,(11)中第二式两边同时乘以μ,然后相加,可以得到

因为0≤μ≤1,所以
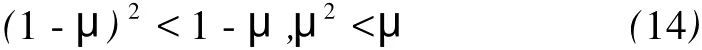
根据(13)和(14)有

因为?c(j)>0,c(j)>0,则有

故不能绝对保证对任意的j≥0,一定存在正数η使得

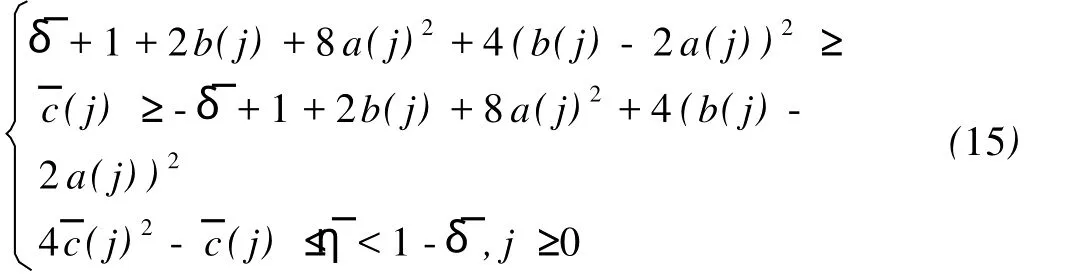
同样根据(9)式有


可使下式成立

但不能绝对保证一定存在正数η使得

成立。
类似前2种情况的讨论,有(10)式和(16)式成立。再由(7)式有对于不等式(17)的右边
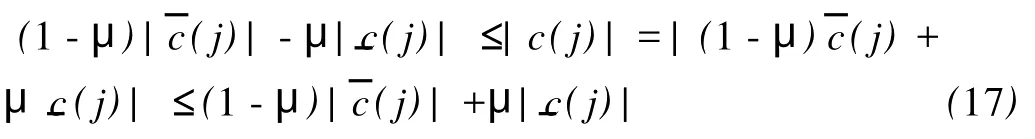

对于不等式(17)的左边,由于0≤μ≤1,所以

则有

综合(18)与(20)两式则有

也即
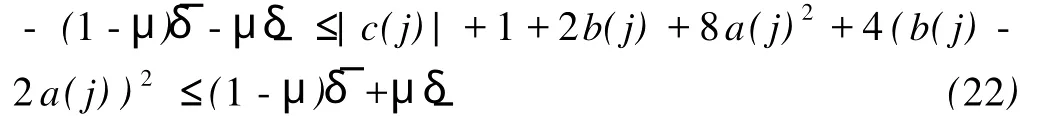
仍取δ=(1-μ)δ?+μ δ,则(22)式可以化为
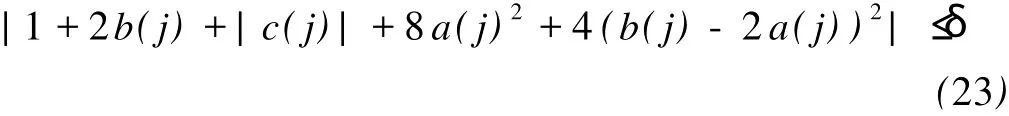
根据(14)式


那么根据(24)式,必有

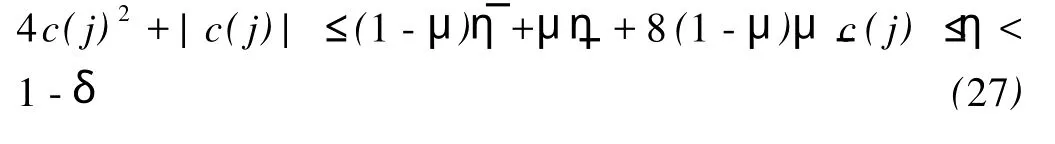
4 主要定理
根据以上3种情况的讨论,可以得到以下关于时滞项含区间系数的2-D离散系统的渐近稳定性定理。定理1 [时滞项含区间系数的2-D离散系统的渐近稳定性定理]



使得(23)与(27)两式成立。再根据引理1,可知结论成立。
至此,本文得到了时滞项含区间系数的2-D离散系统渐近稳定的充分条件。
5 例子
下面利用1个例子来说明本文主要定理的可行性。考虑如下的时滞项具有区间系数2-D离散系统
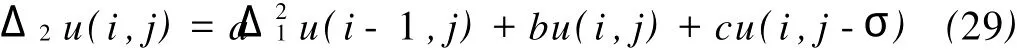

与

取

显然有

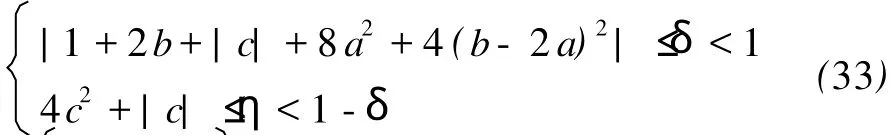
综上所述,对系统(29),有a>0,且存在正数δ,η使得(33)成立,根据引理1,可知系统(29)稳定。
也可根据定理1,此时取

容易得到,系统(29)的系数满足定理1的条件,同样可以得到系统(29)稳定。
6 结论
本文在前人的对时滞2-D离散系统稳定性问题分析的基础上,研究了时滞项含区间系数的2-D离散系统稳定性问题,采用不等式技术,得到了一类时滞项含区间系数的2-D离散系统渐近稳定的1个充分条件,所给的例子说明了结论的可行性。在对区间系数的讨论过程中,对于区间系数的上限和下限同时为正和同时为负的情况,也还可继续讨论该类2-D离散系统的稳定性,将在后文继续研究。
[1] 刘永清,谢胜利.滞后分布参数系统的稳定与变结构控制[M].广州:华南理工大学出版社.1998:134-142.
[2] 杨成梧,陈雪如.2-D奇异线性离散系统渐近稳定性的一类Lyapunov方法[J].控制与决策,2001,16(04):497-49.
[3] 赵胜民,唐万生,李光泉.2-D系统的稳定性[J].自动化学报,2002,28(04):620-624.
[4] Mzrszalek W.Two-Dimensional Discrete Model with Varying Coefficients[J].IEEE Proc,1986,130(40):177-183.
[5] 廖晓昕.稳定性的理论方法和应用[M].武汉:华中理工大学出版社,1998:89-95.
[6] Liu Yongqing.Comparison principle of multi delay neutral difference systems[J].Advance in Modeling and Analysis,1992,36(3):37-50.
Stability of a Class of Discrete 2-D Time-Delays Systems with Interval Coefficients
GAO Cun-Chen,ZHANG Xiao-Rong
(School of Mathematical Sciences,Ocean University of China,Qingdao 266100,China)
The stability is analyzed for a class of discrete 2-D time-delays systems with interval coefficients in this paper.A sufficient condition of asymptotical stability is obtained for the systems by using the technique of inequality to discuss three cases of the interval coefficients.The effectiveness of the proposed method is illustrated by a numerical example.
interval coefficient;time-delay;2-D discrete system;stability AMS Subject Classification: 93C55,93D99
TP13
A
1672-5174(2010)09-159-04
国家自然科学基金项目(60974025);山东省自然科学重点基金(Z2006G11)资助。
2009-06-08;
2010-04-23
高存臣(1956-),男,教授,博导。Email:ccgao@ouc.edu.cn
责任编辑 朱宝象
