基于SPSS的弹簧振子实验数据处理研究

张 燕

(运城学院 工科实验实训中心,山西 运城 044000)

“弹簧振子实验”是大学物理实验课程中的重要实验之一。通过对该实验的研究，学生可以掌握弹簧振子做简谐运动的规律，又加深对胡克定律的理解。该实验在数据处理时，常用的数据处理方法有逐差法和作图法，以往文献物理实验教学和科研工作者也有借助数据处理软件的，如EXCEL、ORIGIN等[1,2]。本文的研究是借助数理统计的实验数据处理方法，这种实验数据处理的方法在大学物理实验数据处理中也有应用[3,4]。利用SPSS软件对测量数据进行回归分析，得到回归模型，利用回归直线的斜率即回归系数，测得弹簧的劲度系数。

1 原 理

1.1 胡克定律

弹簧在受到外力作用下会产生形变。根据胡克定律：在弹性限度内，弹簧所受应力ΔF与单位变形量Δh呈线性关系[5,6]，即

Δf=kΔh

(1)

式(1)中，k为弹簧的劲度系数，ΔF的值为弹簧负载砝码所受的重力mg。通过依次测量出ΔF所对应的Δh值，利用式(1)可以推算出k值。

1.2 简谐振动

设弹簧的劲度系数为k，悬挂负载质量为m负，由于弹簧本身的质量对振动周期有影响，在不可忽略弹簧质量的情况下，其振动周期为

(2)

式(2)中，m0为弹簧本身的质量，c为折合系数(c<0)，cm0为弹簧的折合质量，由上式得：

(3)

由于实验用弹簧选定不变，那么弹簧质量和折合系数一定，由此可见T2与负载质量m负呈线性关系[2,3]，本实验测出不同负载质量时的对应周期，从式(3)的斜率和截距中可求出弹簧的劲度系数k和折合系数c。

2 实验数据处理

2.1 原始数据

原始数据见表1～3。

续表

表2 弹簧及初始砝码质量

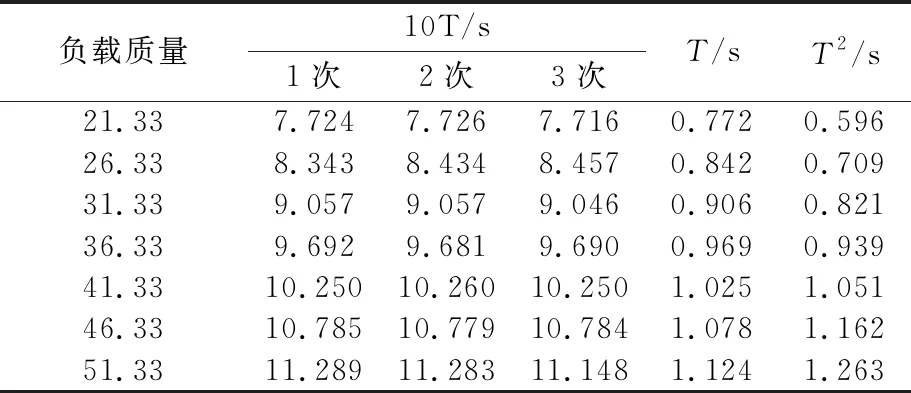
表3 负载质量m负和对应振动周期T

2.2 逐差法

用逐差法对Ai(1,2，……17)的平均值进行处理(见表1)，计算Δh的值：

=28.58 mm

2.3 图解法

2.4 SPSS模型预测法

将表1中的数据带入SPSS，对弹簧所受应力ΔF和伸长量Δh进行一元线性回归分析，分析结果如表4所示：

表4 模型拟合度

从表4的输出结果可以看出，复相关系数R=1.000，决定系数R2=1.000，经调整的判定系数AdjustedR2=1.000，判定系数的取值在[0,1]范围内[7,8]，说明弹簧的形变是由弹簧所受应力的变化引起的，而且预测模型拟合度良好。

从表5方差分析结果可以看出，模型的F统计量的观察值为8.475E5，统计检验的相伴性概率Sig趋于0，置信度远远小于0.01，所以回归是高度显著，即弹簧应变量因所受应力变化的影响显著，可以由弹簧所受的不同大小的应力来预测弹簧的应变，它们所建立的线性关系回归系数存在，且表明预测回归模型较好，具有统计学意义[4,5]。

表5 方差分析

a.Dependent Variable：砝码质量

从表6预测模型系数可以看出，预测模型自变量系数为0.175，常数为0.000[9，10].可以得到预测回归模型为：Y=0.175X以上回归分析中因变量为砝码质量，所以预测回归模型两边同时乘以重力加速度得到弹簧所受应力与弹簧应变的表达式：

表6 预测模型相关分析

Δf=0.175×9.8Δh

由上式可测算得弹簧劲度系数k=1.715 N/m。

3 总 结

利用SPSS数理统计测得的弹簧劲度系数与逐差法和图解法测得的劲度系数百分误差为0.1%。结果表明：逐差法与图解法过程复杂，效率低，容易产生误差，利用SPSS软件对测量数据进行回归分析，求出回归模型，利用回归直线的斜率即回归系数求解弹簧劲度系数，使实验数据处理更加简便和直观。最后，任何实验数据处理的方法都要建立在精确地测量数据之上，实验者的正确的操作步骤、操作技巧和精确地实验方法同样很重要。