运载火箭飞行载荷联合优化控制技术

袁 赫，李静琳，宋征宇，赵永志，徐姗姝，曾耀祥

(1. 北京宇航系统工程研究所，北京 100076；2. 中国运载火箭技术研究院，北京 100076)

0 引 言

长征八号运载火箭(以下简称CZ-8)采用模块化设计思路，即利用现役火箭的成熟箭体模块(芯级或助推)组合成新构型火箭，使其具有良好的继承性、经济性、先进性和适应性。但同时也带来了新的问题，即成熟箭体模块的承载能力与新构型火箭的实际飞行剖面载荷不匹配，导致发射概率过低。

传统运载火箭结构设计一般采用正向设计[1-2]，在目标轨道、运载能力顶层指标及约束条件下，箭体经历初步设计迭代后，总体、气动、弹道、姿态控制多专业协同迭代给出准静态载荷计算所需的计算参数，例如气动力系数分布、发动机推力、qα值(气动载荷因子qα=动压q·攻角α)等，据此开展全箭准静态载荷计算，结合专业综合准静态载荷和动态载荷水平开展箭体结构迭代设计，使其满足结构强度要求的同时保证运载能力指标要求。整个流程正向迭代，箭体结构基于飞行剖面载荷设计，其结构强度必然满足要求。

模块化研制的运载火箭箭体结构强度已确定，不再基于飞行剖面载荷进行设计，已有箭体结构承载能力可能与飞行剖面载荷严重不匹配。CZ-8火箭是模块化研制的代表，在设计初期遇到了这种问题。如果不采取任何载荷控制技术，其飞行剖面载荷结果严重超出了已有箭体的承载能力。直接的解决方案有两个：(1)更改结构，对箭体进行适应性加强，使其能够满足飞行剖面载荷要求，但无疑增加了结构重量，甚至严重影响运载能力，也违背了模块化研制的初衷；(2)牺牲发射概率，如果不加强结构，只能将希望寄托于发射日窗口预报风速远小于设计阶段所采用的统计风场，可能会导致频繁推迟发射。无论哪种解决方案都需要付出沉重的代价。

为了摆脱这一困境，需采取有效的飞行载荷控制技术，目前国内外采取的主要手段有弹道风修、主动减载、发动机节流等。在弹道风修正方面，余梦伦[3]介绍了高空风弹道风修正的原理方法和相关的计算模型，并成功应用在CZ-2E运载火箭上，减载效果显著。Blanchet等[4]介绍了德尔塔运载火箭发射日的风修弹道方案，根据风的变化调整弹道方案，提高发射概率。Chen等[5]给出了无控火箭的风修方法，并定制了相关软件。在主动减载方面，宋征宇团队[6-7]介绍了主动减载在长征系列运载火箭上的应用，并与弹道风修方法进行了比对。韦常柱等[8]为运载火箭设计了主动减载控制器，经过大动压时控制攻角与侧滑角，有效降低气动载荷。Oh等[9]提出了一种带气动攻角反馈的反演滑模控制方案，是一种非线性闭环减载措施。在发动机节流方面，周锡文[10]介绍了一种电磁阀控制的可变喷注器截面双组元变推力液体火箭发动机的组成部分、工作原理和调节过程。Casiano等[11]以美国发动机为中心，对液体推进剂火箭发动机节流进行了详细的调查，比较了不同推力调节方法的优缺点，并对推力调节的应用进行了展望。Betts等[12]讨论了三种成功的节流发动机，并给出应用场景，在减载方面起到了重要作用。

这些成熟技术面向火箭的正向设计，可部分降低飞行载荷。对于CZ-8火箭，经评估各项减载技术减载能力均小于20%，而火箭需减载60%以上，因此这些技术手段单一使用不能达到减载需求，CZ-8火箭的研制需要一种新的设计理念来摆脱这一困境。

在上述背景下，本文开展了基于横向动载荷精细化、弹道风修、发动机节流、主动减载的飞行载荷联合优化控制技术研究，并提出了一种以箭体承载能力为约束，提高发射概率为目标，多种载荷控制技术联合为手段的逆向设计流程。大幅度减载，在不改变箭体结构的前提下提高发射概率，并在CZ-8运载火箭首飞上成功应用。

1 基于飞行载荷联合优化控制技术的逆向设计流程

运载火箭飞行剖面载荷分为准静态载荷和动态载荷，其中准静态载荷主要指由作用时间较长、分布特性相对稳定、幅度及加速度变化平缓的外力引起的箭体截面轴力和弯矩[13]，例如发动机额定推力、平稳风等引起的内力；动态载荷是将运载火箭视为弹性体，在非定常外力下得到的响应结果，例如发动机点火、关机、级间分离引起的轴向冲击载荷，阵风和脉动压力引起的横向弯矩[1]。其中，轴力载荷的大小在整个飞行方案中较为固定，下降空间较小，减载的关键是弯矩，因此本文重点围绕弯矩载荷进行分析研究。

准静态弯矩载荷大小取决于弹道、姿态控制等上游专业的输出参数，主要与气动载荷因子qα值呈正相关。该值在设计阶段由弹道和姿态控制专业根据统计风场进行设计，可以在一定程度上代表运载火箭准静态弯矩载荷的大小，减载可通过降低飞行qα设计值解决。动态弯矩载荷只与火箭本身动力学特性及动态外激励有关，根据火箭本身不同的特性，一般占总弯矩载荷的30%～50%。如果能设法降低动态弯矩载荷，一方面可以降低总载荷，另外一方面可为准静态弯矩载荷“让出空间”，使箭体能够承受更大的qα值，减载效果如图1所示。

图1 减载效果示意图Fig.1 Schematic diagram of load reduction

基于上述分析，CZ-8火箭的弹道、姿态控制、载荷专业提出横向动载荷精细化、弹道风修、发动机节流、主动减载四项技术实现飞行载荷控制。其中，横向动载荷精细化通过优化阵风载荷计算输入降低动态弯矩载荷；弹道风修根据高空风速风向与火箭射向的关系，通过预先调整飞行姿态降低飞行中的攻角，达到降低qα值的目的；发动机节流可令火箭在进入大风区之前降低加速能力降低飞行动压，达到降低qα值的目的；主动减载通过将火箭的横、法向加速度引入控制回路，降低飞行中的攻角，达到降低qα值的目的。

基于上述四项减载技术，CZ-8火箭在研制过程中探索出适用于模块化研制的逆向设计流程，如图2所示，该流程的核心是将运载火箭承载能力引入设计流程的顶层指标及约束条件中，根据初步方案论证结果确定箭体能承担的最大qα值。在该过程中结构系统依据各部段结构的极限承载能力，以及依据初步弹道计算出的轴向载荷反算出各部段能承受的最大弯矩，评估其对应的qα值，该值即为箭体结构能够承受的最大qα，可记为qαs。对弹道、姿态控制上游专业反提出要求，四项减载技术贯穿整个设计流程以达到qαs的要求。

图2 基于飞行载荷联合控制优化技术的运载火箭逆向设计流程Fig.2 Reverse design process based on flight load joint control optimization technology

2 飞行载荷联合优化控制技术

2.1 横向动载荷精细化设计

火箭飞行中的横向动载荷主要考虑火箭飞行运动方程组所组成的闭环系统在外界随机干扰激励下的动响应，体现在箭体结构上为动态弯矩载荷。这些干扰主要有阵风、跨音速区的脉动压力等，采用概率统计的方法在频域进行分析获得输出的统计量，本节对阵风载荷计算进行精细化设计。

2.1.1阵风载荷计算方法

阵风作为随机变量，假定是平稳的、各态历经的随机函数，并且空间各向同性，运载火箭的飞行状态使得阵风各向同性的性质变成了与火箭速度方向垂直和平行两种状态，其功率谱密度也随即有纵向谱Φ1(Ω)和横向谱Φ2(Ω)，在阵风载荷分析中，一般关心横向功率谱密度。阵风扰动在运载火箭各截面均不相同，产生了非定常气动力，为了简便计算将其做准定常处理，同时假设：运载火箭纵轴线与阵风速度W(x,t)在同一平面内；固定坐标系坐标原点位置位于特征时间零秒时火箭质心xT处；运载火箭的xk(箭体坐标系下)截面，从特征时间零秒算起，经过t秒的位置为

xt=Vt+(xT-xk)

(1)

经过t秒后，作用于运载火箭xk截面的阵风速度为

W(xk,t)=W(xk)W(t)=W(t)exp(iΩj(xT-xk))

(2)

则阵风在第xk截面上产生的攻角为

(3)

式中：V为运载火箭飞行速度；Ωj=ωj/V为减缩频率，ωj为箭体结构弹性振动频率。

考虑箭体的弹性振动方程

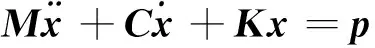
(4)

式中：M为质量矩阵；C为阻尼阵；K为刚度阵；x为箭体站点位移向量；p为阵风作用于箭体的力形成的等效节点力向量。

在已知火箭模态参数的情况下将式(4)投射到模态域得到第j阶振动方程

(5)

式中：qj为第j阶广义位移；ωj为结构第j阶固有频率；ζj为第j阶模态阻尼比；Fj(t)为阵风引起的第j阶广义干扰力，表达式为

(6)

对式(5)进行拉普拉斯变换，并将式(6)代入，得到解耦后的动力学方程在频域内的表征为

(7)

式中：s为拉普拉斯算子；Zj的表达式为

(8)

则该系统的传递函数为

(9)

以阵风横向谱Φ2(Ω)作为系统的输入，在全频域积分，可以得到第j阶广义位移的均方值

(10)

式中：Φ2(Ω)选用火箭常用的阵风功率谱密度Dryden谱[16]，其表达式为

(11)

(12)

利用模态分析得到的模态剪力、弯矩，得到相同概率下箭体截面剪力和弯矩的最大值为

(13)

2.1.2精细化方案

根据阵风载荷计算公式，影响其结果的因素较多，可以分为两类，一类是火箭本身特性参数，另一类是阵风特性参数。其中，火箭本身的特性参数由结构特性确定，无法改变；阵风特性参数具有一定的统计特征，其数值的选取具有一定的经验性，可根据需求进行精细化设计。

图3 阵风载荷随阵风功率谱密度参数变化情况Fig.3 Variation of gust load with gust power spectral density parameters

图4 不同海拔高度阵风风速均方根值Fig.4 Root mean square value of gust wind speed at different altitudes

2.2 弹道优化设计

2.2.1风修正弹道动力学模型

运载火箭在飞行过程中，受到包括发动机推力、气动力、重力等综合作用。对运载火箭上升段弹道来说，由于射程相对较短，地球曲率变化和自转对重力加速度的影响可以忽略，从而简化动力学模型。

(14)

发惯系视加速度为

(15)

式中：φa,ψa分别为发射惯性系下的俯仰角和偏航角。

箭体气动力为

(16)

式中：α,β分别为攻角和侧滑角。

运载火箭在穿过稠密大气时，由于高空风的存在，会产生附加气流攻角，对飞行中的气动载荷产生不利影响。为改善火箭的飞行条件，弹道根据高空风速风向与火箭射向的关系，预先调整飞行姿态，降低飞行中气流攻角，实现降低飞行qα的效果。

如图5所示，在无风情况下，地速VK与空速VA重合，火箭纵轴xb与地速VK的夹角αk即为火箭的攻角α,qα=qαk。当存在高空风时，由于风速VW的影响，VK=VW+VA。此时攻角α即火箭纵轴xb与空速VA的夹角增大为αk+αw，相当于附加了一个风攻角αw,qα=q(αk+αw)=qαk+qαw。

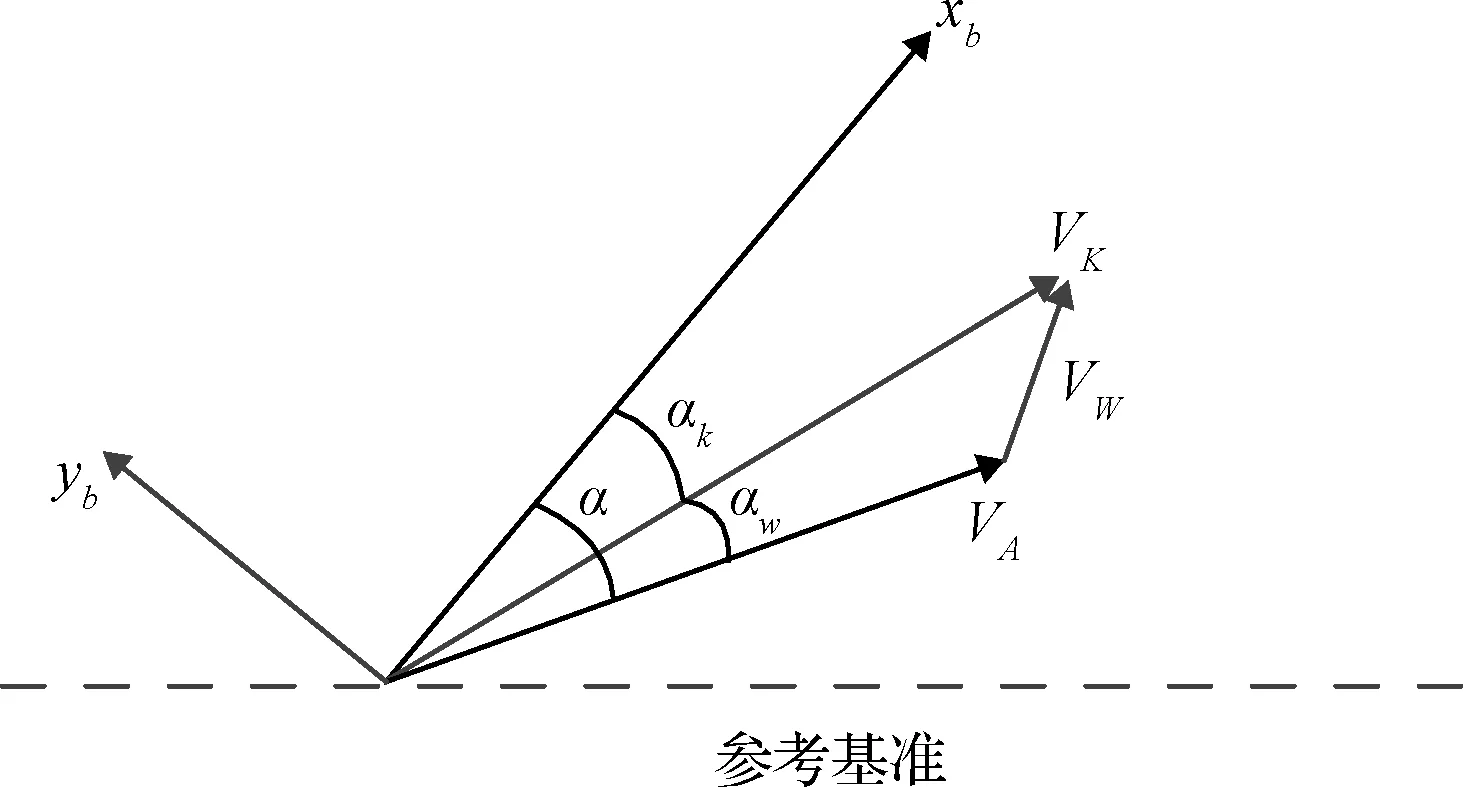
图5 风干扰下俯仰平面矢量关系图Fig.5 Vector diagram of the pitch plane under wind interference

图6 俯仰平面风修正矢量关系图Fig.6 Wind correction vector diagram in the pitch plane

以俯仰通道为例，如图6所示，弹道风修正通过调整火箭姿态角φ，减小箭体纵轴xb与空速VA之间的夹角，从而消除附加风攻角αw产生的附加载荷qαw的影响，以降低飞行qα。风修正俯仰姿态角如下

φp=θvk+αk-αw

(17)

式中：θvk为弹道倾角。

2.2.2发动机节流模型

额定状态下，发动机推力计算方式如下

P=Ispdm

(18)

式中：Isp为比冲。

在节流工作状态下，Isp和dm均会下降，节流状态下，发动机的推力可表示如下

(19)

式中：Ksp,Kdm分别为节流工况下的比冲系数和流量系数。

不同节流比例下的节流系数不同，根据节流的起始时间、节流持续时长和节流比例的不同，各级飞行段的发动机推力可以表示为

(20)

式中：tJL为节流起始时间；ΔtJL为节流持续时间。

2.2.3常规约束条件

(1)初始终端条件

火箭起飞时刻的速度、位置和起飞质量须满足如下约束

(21)

式中：m0为火箭的起飞质量。

为了满足入轨要求，星箭分离时刻的轨道根数须满足卫星对入轨轨道根数的要求

(22)

式中：af为轨道半长轴；ef为偏心率；if为轨道倾角；Ωf为升交点经度；ωf为近地点幅角；ff为真近点角。

进一步考虑子级残骸的落区要求，火箭助推段和一级飞行段关机点的速度位置需满足如下约束

(23)

(2)分级约束

对于多级运载火箭，由于火箭级间分离会导致质量、推力等状态量的不连续。因此，运载火箭上升段弹道优化是一种多段优化问题。在弹道设计中，为了充分利用火箭的推进剂同时确保火箭飞行安全，按照各级可用推进剂量对各级飞行段进行分段，分段约束如下

(24)

同时，各级飞行段之间的状态量需保持连续性，飞行位置和速度需满足约束

(25)

(3)轴向过载

为了满足卫星等有效载荷的力学环境条件，确保卫星安全和正常工作，火箭飞行过程中的轴向过载须满足

(26)

(4)热流约束

为了满足卫星和火箭整流罩等的热力学环境条件，确保卫星和火箭的安全和正常工作，火箭飞行过程中的热流须满足

(27)

(5)控制变量约束

考虑控制系统的控制能力，对火箭的姿态角及姿态角速度进行限制。

(28)

2.2.4目标函数

为了有效降低火箭的飞行载荷，提高发射概率，以火箭飞行过程中的qα为目标函数

J=min(qα)

(29)

2.2.5工程设计

考虑节流、风修正、落区等约束的运载火箭弹道优化设计,是一种多段、多约束的复杂优化问题，求解困难。在工程实践中，通常会将某些约束抽象简化，或者根据工程设计经验，对某些优化参数进行预先设计和确定，使其预先满足某些约束要求，从而有效减少优化问题需要考虑的设计约束，简化求解过程。

2.3 攻摆角优化设计

2.3.1主动减载方法

主动减载是一种通过改变飞行控制结构来降低全箭载荷的技术。具体实现方法是，箭上安装横法向加表，加表测量横法向加速度并引入控制回路，改变发动机摆角以降低气动干扰产生的载荷攻角，从而降低全箭载荷。此时的姿态闭环控制回路变为姿态回路和减载回路两个回路，如图7所示。

主动减载减小载荷攻角的原理如图8所示，当控制结构引入减载回路时，箭机输出的控制摆角改变，导致箭体姿态改变，使得箭体轴由x1变为x′1，弹道攻角由α减小到α′(α′<α)，从而载荷攻角由α+αw减小为α′+αw。

图7 考虑主动减载的姿态闭环控制回路Fig.7 Attitude closed-loop control loop considering active load shedding

图8 主动减载作用下风攻角与弹道攻角的关系Fig.8 Relationship between wind angle of attack and ballistic angle of attack under active load shedding

2.3.2主动减载下的攻摆角计算

以俯仰通道为例说明主动减载下的攻摆角计算方法。俯仰通道的姿态动力学方程可简化考虑为

(30)

式中：Δφ为俯仰姿态角偏差；Δθ为弹道倾角偏差；Δα为弹道攻角；Δδφ为俯仰通道摆角；αwp为平稳风攻角；αwq为切变风攻角，其余为方程系数。

控制方程为

(31)

(32)

式中：lax=xa-xz为加速度表到全箭质心的距离；xa为加速度表安装位置坐标；xz为全箭质心位置坐标。

(33)

由于切变风的变化比箭体质心运动快，可以近似认为在切变风作用下质心的运动可以忽略，忽略箭体运动方程和控制方程的动态项，联立方程可得切变风载荷攻角为：

(34)

3 CZ-8运载火箭应用实例

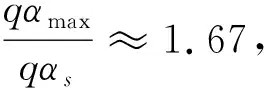
针对该情况，CZ-8运载火箭采用基于飞行载荷联合优化控制技术的逆向设计流程，尽可能提高qαs，减小qαmax，提高发射概率。

3.1 横向动载荷精细化

CZ-8运载火箭阵风载荷设计时充分考虑阵风功率谱计算参数的精细化选取，根据飞行高度进行取值，相比于保守取值方案，整箭弯矩减载效果约11%，以跨音速工况为例展示了精细化减载效果,如图9所示。在箭体承载能力不变的情况下，横向动载荷降低后给准静态弯矩载荷“让出空间”，使得qas提高了约16%。

图9 跨声速工况横向动载荷精细化前后对比Fig.9 Comparison before and after refinement of transverse load under transonic condition

3.2 弹道优化设计

在满足入轨能力的前提下，分别对发动机节流、风修正弹道设计两项减载措施降低飞行qαmax的效果进行评估。仿真中采用的风场为海南冬季风场，并考虑大气偏差、质量偏差、压心位置等偏差的影响，分别对三种工况：无发动机节流+无弹道风修、发动机节流、发动机节流+弹道风修分别进行仿真，结果如图10所示。结果显示发动机节流有效降低qαmax约10.95%，在此基础上弹道风修可再降约5.41%。

图10 统计风场下qα值仿真结果对比Fig.10 Comparison of qα values in statistical wind field

3.3 攻摆角优化设计

在风修节流弹道的基础上进行主动减载，考虑了a0,ag,b2,b3,c3和k3的偏差，上极限和下极限状态参数偏差组合见表1，其中b2取绝对偏差。

表1 参数偏差取值Table 1 Parameter deviation value

(35)

式中：ξ为服从[0, 1]均匀分布的随机变量。

按照上述偏差选取原则进行蒙特卡洛打靶计算，得到俯仰和偏航通道的减载效能系数μφ,ψ，在“大风区”(40～90 s)μφ大致分布在0.8～1.0，μψ大致分布在0.6～0.8，意味着俯仰通道能减小0%～20%的载荷攻角，偏航通道能减小20%～40%的载荷攻角，俯仰通道的减载效能比偏航通道差一些。减载效能具体水平与参数偏差水平、切变风出现高度、风攻角在俯仰和偏航通道的分配比例都有关，而风攻角在俯仰和偏航通道的分配比例由风向和弹道射向的相对关系决定，综合CZ-8火箭的风向和弹道射向，qαmax降低了约18.6%。

综上，横向动载荷精细化将qαs提高了16%，在海南统计风场下弹道优化将qαmax减小16.36%，攻摆角优化将qαmax减小18.6%，qαmax与qαs的比值由1.67下降为0.98，即在统计风场下箭体能够承担的最大qα能力大于飞行过程中历经的最大qα值，由于统计风场可包络绝大部分实测风场情况，在发射月每日实测风场下，qαmax小于qαs的概率大大提高。图11给出了海南发射月每日实测风场下的qαmax的统计结果，30天内有25天的qαmax小于qαs，放行概率可达83%。

图11 海南某年发射当月每日实测风场下qαmax与qαs对比情况Fig.11 Comparison of qαmax and qαs under daily measured wind field through a month in Hainan

4 结 论

本文针对运载火箭模块化研制中面临的结构承载能力与飞行载荷不匹配的弊端，提出了一种基于横向动载荷精细化、弹道风修、发动机节流、主动减载的飞行载荷联合优化控制技术，并建立了以提高放行概率为目标，箭体承载能力为约束，四项减载技术联合控制技术为手段的逆向设计流程。该流程在总体设计阶段引入发射概率作为设计指标，在不改变箭体结构的前提下最大化发射概率。上述方法在CZ-8首飞中成功应用，将方案设计阶段的发射概率从33%提高到了发射日的83%，具有很强的工程应用价值，为运载火箭模块化研制提供了新思路。