空间站和GNSS共视的差别及精度对比分析

2022-11-17刘音华陈瑞琼李孝辉张首刚

宇航学报 2022年10期

刘音华，陈瑞琼，刘娅，李孝辉，张首刚

(1. 中国科学院国家授时中心，西安 710600；2. 中国科学院大学，北京 100049)

0 引言

共视比对技术是目前使用最多的一种时间比对方法，该技术的出现距今已有上千年历史，从古代以月食、流星等作为共视比对参考源的分钟级精度的时间比对[1]，到以罗兰导航信号作为共视参考源的微秒级时间比对[2]，再到以导航卫星作为共视参考源的纳秒级时间比对[3]，共视时间比对的精度一直在提高。

导航卫星共视时间比对技术的出现已有30多年，随着导航系统的建设和关键技术的发展,其时间比对精度一直在提高，导航卫星共视是现阶段用于远距离高精度时间比对领域的主要方法[3-5]。科技的进步日新月异，现阶段许多基础前沿领域对时间比对精度提出了更高的要求[6-8]。中国正在建设的载人航天空间站和欧洲空间原子钟组(Atomic clock ensemble in space，ACES)计划，本文把两个系统统称为空间站，在空间站上均搭载高精度原子钟组，空间原子钟在近地微重力环境下具有比地面原子钟更优的性能[9-11]。利用空间站对地的高性能微波时间比对链路，理论上可以实现比导航卫星更高的共视时间比对精度[12-16]。

但是空间站轨道特征和导航卫星差异很大，空间站在低轨运行，共视时间比对误差的相关性远低于导航卫星共视，特别是轨道误差的影响，会超过导航卫星。另一方面，低轨特性还限制了空间站的覆盖区域，会造成共视时间比对的盲区。近年来低轨卫星的应用成为定位导航授时(PNT)领域的热点，但国内外学者大多都利用其进行全球导航卫星系统(GNSS)星座的补充增强，用以提升PNT服务性能[17-20]。低轨卫星共视技术方面的研究文献较少，有国内学者把低轨卫星空间碎片当成共视参考源，其目的是利用光学原理确定该空间碎片的位置[21]，而不是时间比对。本文率先研究低轨空间站共视比对技术，对空间站和导航卫星共视技术进行深入的对比分析，研究两者的误差分布特性和能达到的共视时间比对性能，为利用空间站和其他低轨卫星进行共视时间比对提供技术基础。

本文首先介绍了共视时间比对的基本原理，接着针对共视技术的需求，分析了空间站和导航卫星在系统设计方面的差异，分别结合导航卫星和空间站共视所能达到的精度分析了两个系统共视所需要考虑的误差源。最后，通过实际测试和仿真实验相结合的方式，对比了空间站和导航卫星的共视性能。对比实验表明，轨道误差是影响空间站共视比对精度的主要误差源，在不增加其他修正手段的情况下，单纯的空间站共视精度在百皮秒量级，比导航卫星共视高一个数量级。

1 共视时间比对的基本原理

导航卫星共视实现的是纳秒级的时间比对，空间站共视的目标精度至少要高一个数量级。为了同时满足空间站和导航卫星共视时间比对精度要求，以高精度的广义相对论的时间比对理论作为基础来建立数学模型，充分考虑地球引力时延等精细误差的影响[11,22-24]。在广义相对论地心非旋转坐标系(Geocentric celestial reference system，GCRS)中，介绍共视时间比对原理。

共视时间比对的基本原理如图1所示，利用空间原子钟S作为参考源，实现两地面站间的高精度共视时间比对。A, B两站分别观测本地时间与空间原子钟的钟差，通过数据交互网络交换测量数据，求差后可以得到A, B两站的时间偏差为ΔTAB=TA-TB，所求结果包含两站的传输链路时延测量误差ε(dSA)-ε(dSB)。

图1 共视时间比对基本原理Fig.1 Principle of common-view time comparison

假设地面站A, B在t0时刻接收到空间参考源(空间站或导航卫星)的时间比对信号，两站与空间参考源的钟差可以表示为式(1)和式(2)。

(1)

(2)

式(1)和式(2)相减，可以得到共视时间比对的计算公式：

(3)

综合式(1)至(3)可以看出，共视时间比对其实是两站各项延迟分量之间的差分运算。由于空间载荷下行发射通道的硬件时延和周期性相对论效应引起的时延在同一时刻与地面站无关，因此通过共视差分运算可以抵消这部分时延。通过共视差分还可以抵消两站其他延迟分量之间的共有误差，改善时间比对的精度。

2 空间站和导航卫星系统设计方面的差异

空间站和导航卫星在系统设计层面产生的并对共视时间比对造成影响的差异特性主要体现在以下三个方面：轨道特性的差异、搭载原子钟性能的差异、下行信号体制的差异。

1) 对比两大系统的轨道差异。空间站(包括ACES和中国空间站)运行在近地环境下，轨道高度大约为400 km，运行速度远快于导航卫星，平均轨道周期大约为1.5 h，一天可视的飞行周期大约为9个，每个轨道周期对于单个地面站的平均可视时间也非常短，高度角截止角为0°时大约在400 s左右[9,15-16]。因此每天只能在极少数的时间内利用空间站进行共视时间比对。还有些地区属于空间站共视的盲区，不能同时可视空间站，例如喀什和三亚、长春和昆明。

而GNSS多为中高轨道卫星，且卫星数目多，可以利用GNSS卫星进行不间断的共视时间比对[25-27]。例如，GPS系统有20多颗中轨卫星，轨道高度大约为20000 km，轨道周期为11 h 58 min，可以为全球用户提供不间断的时间服务；北斗系统，既有高轨卫星，还有倾斜轨道和中轨卫星，也可以利用北斗卫星进行实时的共视时间比对。

2) 对比分析空间站原子钟和导航卫星星载原子钟的差异。空间站上搭载的原子钟比导航卫星星载原子钟性能更优，一方面空间站的近地微重力环境使原子钟具有比地面原子钟更好的稳定性，另一方面空间站原子钟比导航卫星原子钟性能级别更高。ACES系统空间载荷搭载两台高精度原子钟，一台为激光冷原子铯钟(PHARAO)，另一台为空间主动型氢钟(SHM)。PHARAO预期频率稳定度达到10-13×τ-1/2(τ为平滑时间)，频率准确度达到3×10-16。SHM秒稳优于1.5×10-13，天稳优于1.5×10-15。ACES空间时频信号将兼顾两个原子钟的性能，秒稳优于1×10-13，天稳优于1×10-15。中国空间站将搭载超高性能的光钟，综合时频信号的稳定度至少比ACES高一个数量级。而导航卫星星载原子钟多为铷钟和铯钟，Galileo卫星上还有被动型氢钟，但星载原子钟输出时频信号天稳定度仅在10-14量级，较空间站原子钟稳定性至少低一个数量级。空间站和导航卫星原子钟是共视时间比对的参考源，尽管从理论上分析共视原理抵消了空间原子钟的影响，但由于两个共视站点之间的时钟基准不同、信号传输路径不同，不可能做到绝对的同时共视，因此也不能完全抵消空间原子钟的影响。高稳定性的空间站原子钟组是持续优化空间站共视的一个有利的基础条件。

3) 对比分析两者的信号体制差异。空间站下行信号码速率比导航卫星要大，频率较导航卫星要高。空间站下行信号码速率为100 MHz，是导航卫星P码速率的10倍，因此空间站下行信号伪码测距精度比导航卫星要高。导航卫星下行信号一般在L频段，空间站下行信号工作频点在Ku和Ka波段，空间站下行信号载波相位观测量的精度比导航卫星要高。由于电离层延迟与工作频点的平方成反比，空间站下行链路的电离层延迟至少比导航卫星小两个数量级。电离层延迟是导航卫星共视的主要误差源，而对于空间站共视来说，只需要采用双频修正法即可获得皮秒量级的电离层延迟计算精度，电离层延迟误差修正将在下文进行详细的对比分析。因此，导航卫星系统的信号体制限定了其共视比对精度在纳秒量级，而空间站的下行比对链路比导航卫星性能更优，可以支持实现更高精度的共视比对。

3 空间站和导航卫星共视关键误差源影响差异

由于空间站共视和导航卫星共视的目标精度不一致，前者至少在百皮秒量级甚至更高，后者在纳秒量级。基于式(3)的共视基本原理，空间站共视和导航卫星共视在各项时延分量误差的处理策略上也不相同。

3.1 星地几何距离

几何距离利用空间站或导航卫星下行信号发射天线相位中心坐标和地面站接收天线相位中心坐标进行计算，以A站为例，计算公式如式(4)所示。

ρSA=S(tsnd)-A(trcv)

(4)

式中:S(tsnd)表示空间参考源在下行信号发射时刻tsnd的位置矢量，A(trcv)表示地面站A在下行信号接收时刻trcv的位置矢量。因此，几何距离计算精度主要受空间站或导航卫星位置精度以及地面观测站位置精度的影响。地面观测站的坐标一般都会进行高精度的标校，本文重点考虑空间站和导航卫星位置的影响。

式(3)中忽略其他项的影响，等号两边对空间参考源的位置求导，可得到式(5)，其中，dXS为空间参考源位置的导数,ρSA和ρSB为空间参考源到两个地面站之间的距离矢量。

(5)

假设地面站A与地面站B到空间参考源的几何距离均近似为轨道高度h,ρAB为两个地面站之间的基线向量，则可以得到以下关系式。

(6)

由式(6)可知，空间参考源位置误差对共视时间比对的影响与参考源轨道高度、两地面站之间的基线长度和位置误差本身的大小有关。

对于导航卫星共视，卫星的轨道高度一般在20000 km左右，地面基线最长也就上千公里，按照2000 km估计，卫星位置误差按1 m估计，则卫星位置误差对共视时间比对的影响小于0.3 ns。对于纳秒量级的导航卫星共视比对目标精度，仅通过共视的差分原理就可以抵消卫星位置误差的影响，满足目标精度要求。

空间站的轨道高度大约为400 km，如果两地面站之间的基线长度大于轨道高度，空间站位置误差对共视的影响可能会得到放大。空间站位置误差对共视的影响与位置误差矢量大小、方向以及空间站与两地面站之间的视线方向有关，下文通过仿真来进行分析。

由于空间站定轨数据提供的是空间站质心的位置坐标，相对于下行信号发射天线相位中心坐标有一定的距离偏差，需要将质心坐标修正到下行天线相位中心。因此，空间站位置误差主要由轨道误差、空间站姿态误差、相位中心标定误差、运动轨道修正误差等因素共同导致，下面通过仿真逐一分析各误差源通过几何距离对空间站共视比对的影响。

3.1.1轨道误差

空间站上搭载高性能GNSS接收机，提供优于10 cm的轨道位置服务。把轨道误差分解到R,T,N三个维度，以轨道误差分别为[0.100] m,[00.10] m和[000.1] m进行仿真，地面站位置分别设置为西安、北京和上海，仿真时长为1 d，空间站轨道误差对几何距离的影响如图2所示,统计结果如表1所示，表中单位为皮秒。

图2 轨道误差对几何距离的影响Fig.2 Effect of orbital error on geometric distance

表1 轨道误差对几何距离的影响Table 1 Effect of orbital error on geometric distance

从图2可以看出，空间站轨道误差对几何距离的影响与轨道误差矢量的方向和幅值相关，不同误差矢量对不同地面站间的共视时间比对的影响不同。从图2(a)可知，径向方向的轨道误差对共视比对的影响较小，此时轨道误差对两站的空间相关性高，共视差分能抵消部分轨道误差的影响，10 cm幅值的轨道误差产生的几何距离误差不超过200 ps。从图2(b)和图2(c)可知，切向和法向的轨道误差对共视影响呈现出放大效应，10 cm幅值的轨道误差对共视的影响最大接近500 ps。但是，不管轨道误差是图2中的哪种情况，大多数情况下，共视差分运算都能削弱轨道误差对时间比对的影响。表1的统计数据也证明了该观点，10 cm幅值的轨道误差在一天的可视周期内对通过几何距离导致的共视均方根误差不超过150 ps。因此，部分时刻轨道误差对空间站共视的影响会被放大，但大多数时候共视差分作用能削弱轨道误差的影响。

上述是以轨道误差分布在R, T, N三个方向为例进行分析的，对于轨道误差分布在其他方向的情况也有类似的结论，因为任何方向的轨道误差都可以分解到R, T, N三个方向。

3.1.2姿态误差

不同的姿态角会有不同的空间坐标转换矩阵，空间站姿态误差会导致下行天线相位中心坐标误差，对几何距离的修正产生影响从而影响共视比对精度，但姿态误差的影响量级小于轨道误差的影响。对导航卫星纳秒量级共视精度来说，姿态误差的影响可以忽略不计，但空间站共视需要考虑这部分的影响。

设置如表2所示的姿态误差，表中单位为角秒。仿真分析空间站姿态误差通过几何距离对共视比对的影响，统计结果如表3所示，表中单位为皮秒。

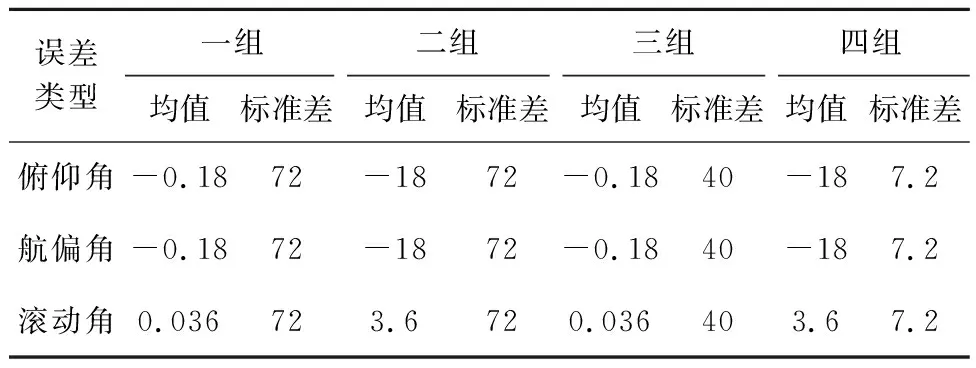
表2 姿态误差仿真参数Table 2 Simulation parameters of posture error

同时给出了标准差和均方根误差,两者的计算公式分别如式(7)和式(8)所示。

(7)

(8)

式(7)和式(8)中，xi为姿态误差产生的几何距离误差，μ为xi的统计平均值，N为样本数目。

对表2设置的姿态误差进行两两比对分析。第一组和第二组姿态误差均值不同，标准差相同，通过表3的对比可以看出，两组姿态误差的标准差相同，引入的共视误差标准差也几乎相当。第二组和第四组、第一组和第三组属于姿态误差均值相同，标准差不同的情况，通过表3的对比可以看出，姿态误差的恒定分量相同，几何距离误差的均值也几乎相当。

由此可知姿态误差的恒定分量主要影响共视比对误差的均值，姿态误差的随机分量主要影响共视比对误差的标准偏差。在姿态误差的随机分量相同的情况下，对共视误差的标准偏差影响基本相同。在姿态误差的恒定分量相同的情况下，对共视误差的统计均值影响基本相同。十几个角秒的姿态恒定误差通过几何距离对共视准确性的影响为几个皮秒，角秒量级的姿态恒定误差对空间站共视准确性的影响可以忽略。70″的姿态随机误差对共视的影响达到近20 ps，40″和7″的姿态随机误差对共视的影响均为几个皮秒。

表3 姿态误差对共视影响Table 3 Effect of posture error on CV

3.1.3相位中心标定误差

星载天线相位中心标定误差一般在毫米量级，对导航卫星共视的影响完全可以忽略不计，但空间站共视目标精度更高，需要进行深入分析。

把空间站下行天线相位中心标定误差分别设置为0.5 mm, 1 mm, 3 mm和5 mm，其对几何距离均方根误差的影响统计结果如表4所示。

由表4可知，相位中心标定误差增加，对空间站共视的影响也增大。5 mm标定误差，西安-北京的共视统计误差最大，约为12 ps。

表4 相位中心标定误差对共视影响Table 4 Effect of antenna phase center error on CV

3.1.4运动轨道修正误差

在星地链路时间比对解算过程中，一般以地面站时钟作为参考基准，式(3)的参考时间为地面站的接收时刻trcv,由于空间站和导航卫星处在不断运动状态，需要对其运动轨道进行修正，也就是需要得到它们在发射时刻tsnd的位置坐标。利用卫星在信号接收时刻的位置矢量S(trcv)对下行信号传播时间t′进行估计，对卫星的位置矢量进行建模，通过模型内插得到空间站或导航卫星在发射时刻的位置坐标S(tsnd)，该位置坐标和真实坐标存在一定的偏差，为运动轨道修正误差。

对导航卫星纳秒量级的共视目标精度来说，可以忽略运动轨道修正误差，本文重点分析空间站共视中这部分误差的影响。利用二次多项式对空间站在信号发射时刻附近的坐标进行建模，内插得到发射时刻的坐标S′(tsnd)，再结合真实坐标S(tsnd)，仿真分析运动轨道修正误差通过几何距离对共视时间比对均方根误差的影响。仿真统计结果表明，运动轨道修正造成的空间站共视时间比对误差在皮秒量级，对西安-上海共视影响约为8 ps，对西安-北京、北京-上海共视影响约为5 ps。

综合上述分析可知，在10 cm的轨道误差、70″的姿态误差、5 mm的相位中心标定误差下，由于几何距离计算误差引入的空间站共视时间比对误差大约为180 ps。而对于纳秒量级的导航卫星共视比对来说，可以忽略这些误差项的影响。

3.2 电离层延迟

空间站和导航卫星信号传输过程中均要经过电离层，需要修正电离层延迟。由于电离层延迟数量与信号频率的平方成反比，电离层延迟对空间站和导航卫星共视的影响并不相同。以IGS发布的垂直电子含量文件作为基础数据来分析空间站和导航卫星信号的电离层延迟，图3为空间站20 GHz下行信号的垂向电离层延迟，图4为GPS卫星1.2 GHz下行信号的垂向电离层延迟。

图3 空间站垂向电离层延迟(20 GHz)Fig.3 Vertical ionosphere delay of the space station (20 GHz)

图4 GPS垂向电离层延迟(1.2 GHz)Fig.4 Vertical ionosphere delay of GPS (1.2 GHz)

从图3和图4可以看出，在同样的电离层穿刺点电子含量的情况下，空间站垂向电离层延迟最大在210 ps左右，而GPS系统的电离层延迟在几十纳秒量级。

电离层延迟一般通过双频伪距观测量的组合方法进行计算，忽略硬件时延标定精度的影响，电离层延迟的解算精度受伪距观测量的影响。式(9)为空间站20.8 GHz和26.8 GHz频点的下行信号组合计算电离层延迟的公式，式(10)为GPS L2和L5频点的下行信号组合计算L5频点电离层延迟的公式。

(9)

(10)

空间站下行伪码观测量的精度优于1 ps，式(9)经过了一次伪距观测量的组合，可以估算出电离层延迟的计算精度大约为4 ps，共视差分作用相当于再进行了一次噪声组合，由此可以估计由于伪码观测量噪声导致的电离层延迟误差引入的共视误差大约是6 ps。导航卫星系统的伪码观测量的精度大约为0.5 ns，由式(10)可以估算出导航卫星系统电离层延迟误差引入的共视误差大约是3 ns。

由电离层延迟误差对共视的影响分析可知，受限于信号频点和观测量的精度，导航卫星系统实现的共视精度为纳秒量级。受益于空间站下行信号的高频点优势，电离层延迟的计算精度在皮秒量级，电离层延迟对共视比对的影响较小，也为皮秒量级。

3.3 引力时延

在欧几里德空间，光的传播速度为常数C。但在引力场中，光传播速度不是常数，因此产生引力时延，计算公式如式(11)所示。

(11)

式中：G为牛顿引力常数；M为地球质量；rS和rA分别为卫星和地面站到地心的距离。

引力时延的量级很小，导航卫星共视不需要考虑。对空间站的引力时延进行仿真，地面站选取西安，一天的仿真结果如图5所示。

由图5可见，空间站下行信号受地球皮秒量级的引力时延影响，对于百皮秒或者几十皮秒量级的空间站共视需要修正引力时延。结合式(11)可知，引力时延计算时用到空间站质心坐标，因此需要考虑空间站位置误差的影响。但由于引力时延本身的量级就小，轨道误差和空间站运动引入的引力时延计算误差更小，通过仿真可知，空间站位置误差通过引力时延对共视的影响在1×10-7皮秒量级，完全可以忽略不计。

对于流层延迟和地面接收设备的硬件时延，它们对空间站和导航卫星共视的影响相同。但空间站共视的目标精度比导航卫星共视要高，对气象参数的观测精度要求更高，对流层延迟的计算方法也更复杂。现有技术表明，利用微波辐射计反演大气水汽含量的方法，对流层延迟的计算精度可以达到十皮秒量级甚至更高。同理，空间站共视对地面观测设备硬件时延的稳定性和标定精度要求比导航卫星接收机也要高。

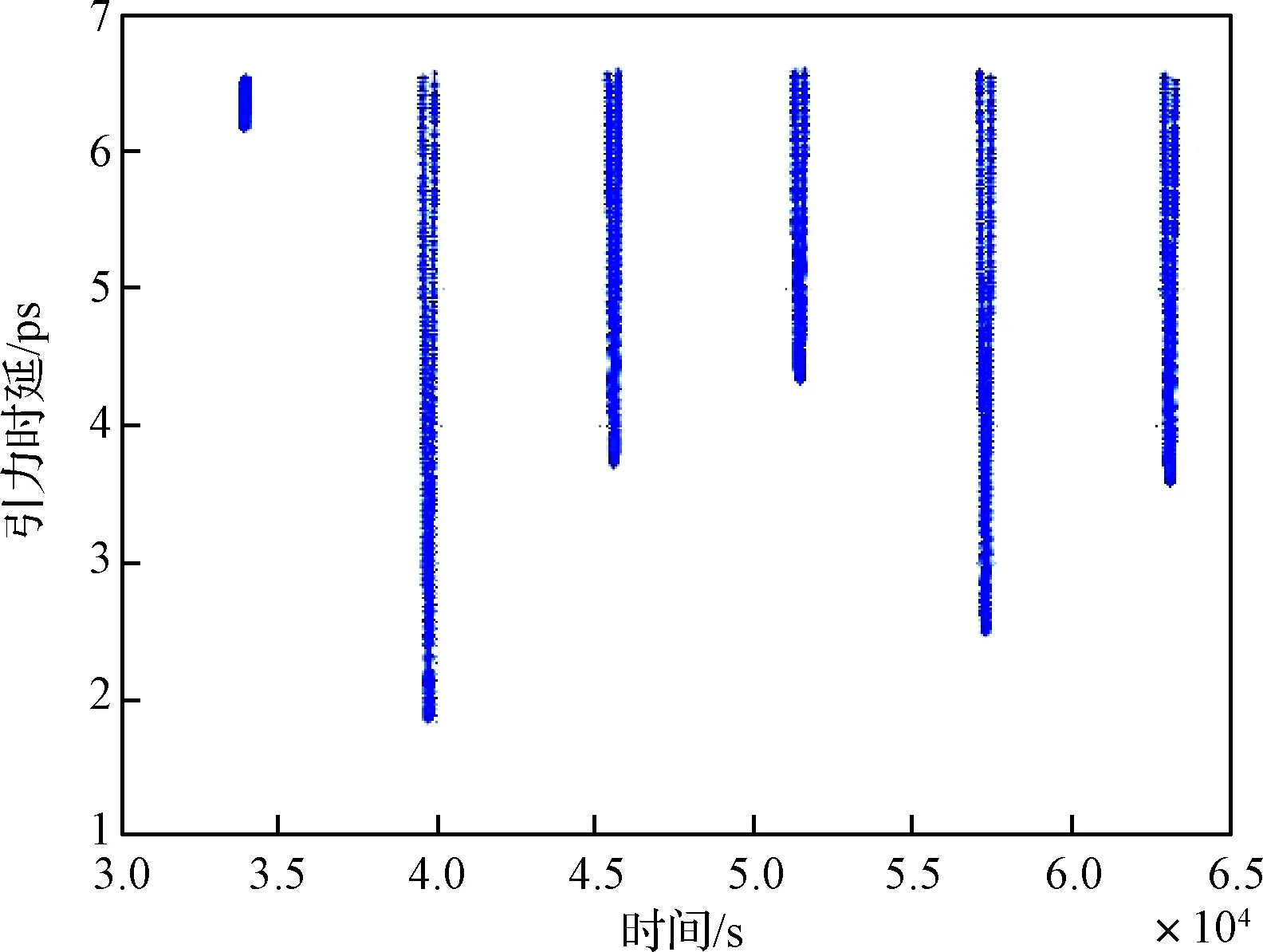
图5 空间站引力时延Fig.5 Gravitation delay of the space station

通过上述对关键误差源影响的对比分析可知，空间站和导航卫星共视在误差处理方面的差异主要体现在几何距离、电离层延迟和引力时延方面。只有几何距离误差对空间站共视的影响达到百皮秒量级，其余误差项的影响都在十皮秒量级甚至更小。其中，轨道误差是影响几何距离误差、限制空间站共视精度进一步提升的主要因素。电离层延迟修正方面，空间站共视比导航卫星优势要大，修正精度更高。此外，空间站共视瞄准百皮秒甚至十皮秒的目标精度，还需要考虑其他精细误差的修正，例如地球引力时延。

4 空间站和导航卫星共视性能对比

在上述空间站和导航卫星各项关键误差对比研究的基础上，利用仿真平台开展时间比对站点位于西安、天津的空间站共视仿真实验，利用GNSS接收机开展西安、天津的导航卫星共视实测实验，对两者的性能进行对比分析。

4.1 空间站共视仿真结果

西安-天津共视仿真实验中，姿态误差<72″，相位中心标定误差<1 mm，轨道误差<10 cm，伪距观测量噪声1 ps，高度角截止角10°，两路下行信号频点分别为20.8 GHz和26.8 GHz。西安原子钟的秒级稳定度设为5×10-12，天稳定度设为3×10-14;天津原子钟的秒级稳定度设为6×10-13，天稳定度设为1×10-14。电离层延迟利用国际GPS服务中心提供的电离层穿刺点电子含量文件进行仿真，双频伪距观测量法进行解算。在仿真中没有考虑对流层延迟误差。

西安-天津空间站共视时间比对的误差如图6所示，横坐标为一天的秒累积数，纵坐标为空间站共视误差。由图可知，西安和天津利用空间站下行信号进行共视时间比对，一天的共视周期为5个，在不考虑对流层延迟误差的情况下，最大共视误差约为500 ps，误差波动范围约为500 ps。对图6中的误差进行统计，均值为188.6 ps，标准偏差为113.2 ps，均方根误差为220 ps。

图6 西安-天津空间站共视仿真结果Fig.6 Space station common-view simulation result between Xi’an and Tianjin

4.2 导航卫星共视实测结果

为了更好地和空间站共视进行性能对比，进行了两组导航卫星共视实验。第一组为零基线共钟共视实验，第二组为西安-天津导航卫星共视实验。

零基线共钟共视实验中，两台GNSS接收机均放置在临潼，共用一个接收天线，利用功分器进行卫星信号的分发。两台接收机采用同源的参考时钟信号，时钟电缆等长。因此从理论上分析可知，该共视比对的结果应该在零值附近，共视数据的波动反映了两台接收机接收通道的噪声起伏。共视比对软件对每秒的观测数据进行平滑滤波，每分钟产生一组共视比对结果，一天的零基线共视数据如图7所示。

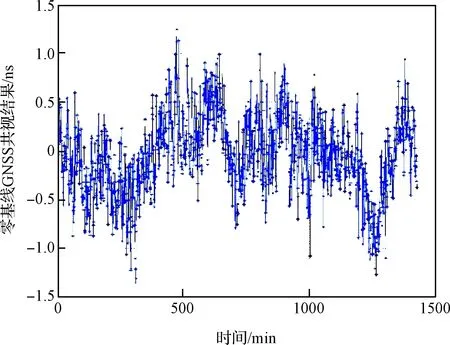
图7 零基线导航卫星共视结果Fig.7 Zero-baseline common-view results of GNSS

由图7可知，零基线共视结果在零值附近波动，波动范围约为3 ns。对图中数据进行统计，均值为-0.051 ns，标准偏差为0.41 ns，统计结果和理论预期一致。

西安-天津导航卫星共视实验中，一台GNSS接收机位于西安临潼，时钟参考信号为UTC(NTSC)，另一台接收机位于天津武清，时钟参考信号来源于铷原子钟，该铷原子钟受共视数据的驾驭，与西安的参考时钟信号UTC(NTSC)同步。一天的共视结果如图8所示。

从图8可以看出，西安-天津的导航卫星共视结果波动范围约为8 ns，明显大于零基线共视时的波动范围。对图中数据进行统计，均值为0.048 ns，标准偏差为1.136 ns。

对比图6和图8可知，空间站共视误差的波动范围只有500 ps，标准偏差为113.2 ps，而导航卫星共视结果波动范围达到了8 ns，标准偏差为1.136 ns。而且导航卫星共视的数据经过滤波处理，噪声被进一步降低。由此可知，空间站共视比对的精度至少比导航卫星共视高一个数量级。空间站共视性能主要受限于轨道误差，在空间站共视的轨道误差精密修正技术得到突破以后，空间站共视精度有望达到几十皮秒量级。