带有控制变量变化率约束的伪谱轨迹优化方法
2022-11-17赵吉松张金明程晓明刘蛟龙
赵吉松,尚 腾,张金明,程晓明,刘蛟龙
(1. 南京航空航天大学航天学院,南京 210016;2. 北京航天自动控制研究所,北京 100854)
0 引 言
轨迹优化对于导弹等飞行器的制导控制系统设计和总体设计具有重要意义[1-4]。轨迹优化问题本质上属于最优控制问题,其求解方法主要分为间接法和直接法[5]。间接法借助变分法或者最大值原理,把泛函优化问题转化为两点边值问题求解;直接法通过对控制变量和/或状态变量进行离散把泛函优化转化为非线性规划(Non-linear programming,NLP)问题,然后采用各种非线性规划算法求解,比如基于序列二次规划(Sequential quadratic progra-mming,SQP)算法的SNOPT[6]和基于内点法的IPOPT[7]。直接法中的配点法[5]由于不需要推导最优性必要条件,并且对初值的敏感性较低,容易收敛,近年来得到广泛研究和应用。特别是其中的伪谱法[8-11]由于具有快速收敛性和较高优化精度,近年来成为轨迹优化和最优控制领域一种非常常用的数值优化方法。其中,开源软件GPOPS[11]更是推动了伪谱法的发展和应用,逐渐发展为行业标准。
对于轨迹优化而言,控制变量的变化率约束和端点约束具有重要工程价值,甚至影响轨迹方案的可行性。以导弹为例,初始攻角通常由发射条件给定,有时为了达到更好的攻击效果对末端攻角也有限制。在实际飞行过程中,还需要对攻角变化率进行限制。对于流量可调的超燃冲压发动机,不仅攻角变化率有约束要求,发动机的流量变化率也有严格的约束要求[12]。在轨迹优化时如果不考虑这些约束可能会导致优化的控制变量变化率过大甚至发生突变,制导控制系统难以对其进行跟踪。为了考虑控制变量的变化率约束和端点约束,目前常用的处理方式是引入控制变量的导数作为虚拟控制变量,将实际控制变量转换为状态变量[12-14]。这种处理方式的优点是形式简单,只需要增加1个状态变量和1个状态方程,对轨迹优化方法的继承性比较好,几乎不需要对轨迹优化方法进行改动。但是,这种引入控制变量导数作为虚拟控制变量的处理方法会带来一些问题[5]。一方面,引入新的状态变量显然增加了状态变量和状态方程的个数,进而增加了离散后的NLP的约束和优化变量的个数。另一方面,增加的控制变量微分方程为线性微分方程,很可能会产生奇异弧进而引起虚拟控制变量振荡甚至发散。这两方面原因都会增加NLP的求解难度(需要更多的迭代次数才能收敛,甚至不收敛)。
最优控制领域的著名学者Betts[5]在研究局部配点法时提出一种直接施加控制变量变化率约束的方法,其思路是采用有限差分法逼近控制变量的变化率,从而将控制变量变化率约束转化为相邻离散节点的控制变量的线性约束。Betts将该方法成功用于局部配点法的梯形离散格式(二阶格式)和Hermite-Simpson格式(四阶格式),避免了传统方法在处理控制变量变化率约束时需要引入虚拟控制变量以及由此导致的虚拟控制变量振荡问题,容易收敛。该方法能够方便地施加控制变量变化率约束,并且添加的控制变量变化率约束全部为线性约束,计算量比较小。与局部配点法相比,伪谱轨迹优化方法[8-11]在计算效率和精度方面具有更好的综合性能,近年来得到了快速发展和广泛应用,但是目前公开文献中还没有基于伪谱法开展直接施加控制变量变化率约束的研究。如果将Betts针对局部配点法提出的直接施加控制变量变化率约束的方法与伪谱法相结合,有可能使伪谱法能够方便、快速地求解带有控制变量变化率约束的轨迹优化问题,这对于拓展伪谱法的功能和性能显然具有重要意义。
本文在传统多区间伪谱法的基础上,引入一种控制变量变化率约束和端点约束的处理方法,以空空导弹轨迹优化问题和临近空间高超声速滑翔轨迹优化问题为例,通过数值仿真和对比验证了所建立的控制变量变化率约束处理方法的有效性。
1 带有控制变量变化率约束的轨迹优化方法
1.1 多区间Radau伪谱法
与全局伪谱法相比,多区间伪谱法[11]具有更高的计算效率。轨迹优化本质上是最优控制问题。为了便于描述,本节以一般形式的Bolza型最优控制问题为例,介绍多区间Radau伪谱法。
一般形式的Bolza型问题可描述为:求解控制变量u(t)∈Rm,使得如下目标函数最小化

(1)
式中:M:Rn×R×Rn×R→R,L:Rn×Rm×R→R,x∈Rn,u∈Rm,t∈[t0,tf]⊆R。
状态方程为
(2)
端点条件为
E(x(t0),t0,x(tf),tf)=0
(3)
路径约束为
C(x(t),u(t),t)≤0,t∈[t0,tf]
(4)
式中:f:Rn×Rm×R→Rn;E:Rn×R×Rn×R→Re;C:Rn×Rm×R→Rc。方程(1)~(4)所描述的连续最优控制问题称为Bolza型最优控制问题。
为了便于应用伪谱法对上述一般形式的最优控制问题进行离散,需要将最优控制问题的时间区间t∈[t0,tf]变换至τ∈[-1,+1],变换方式如下:
(5)
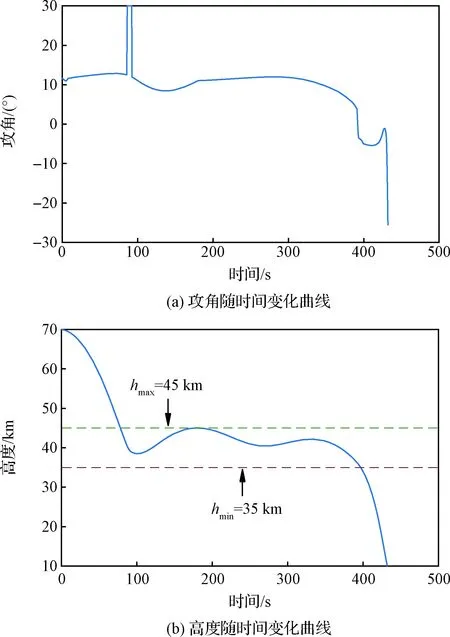
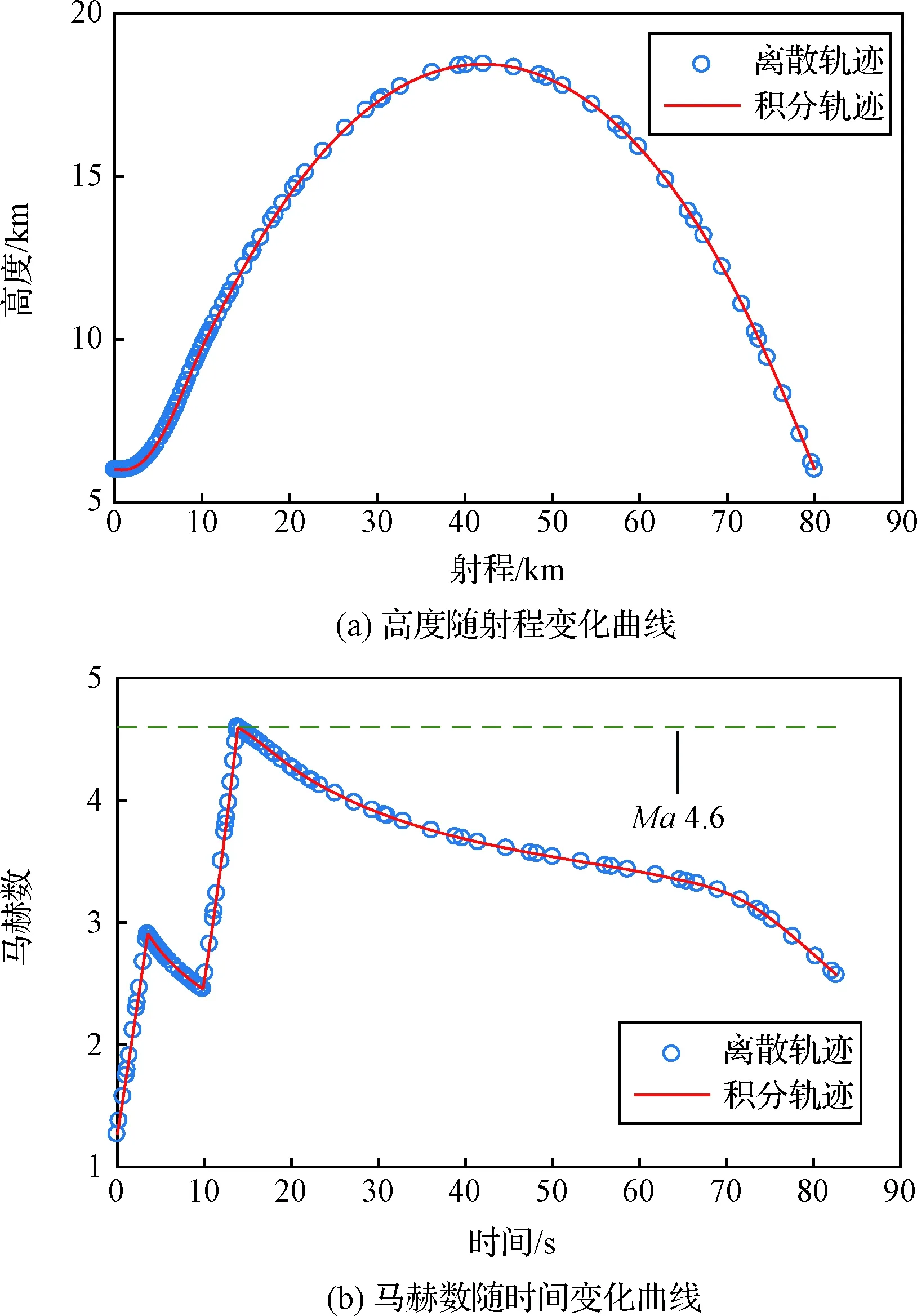
多区间伪谱法将时间区间τ∈[-1,+1]划分为K个子区间Ik=[Tk-1,Tk],k=1,…,K,其中-1=T0 (6) (7) 将方程(6)中X(k)(τ)关于τ求微分得到 (8) 将方程(2)和(8)相结合,可以得到状态方程在区间Ik(k=1,…,K)上的离散形式为 i=1,…,Nk (9) 目标函数(1)的离散形式为 (10) 端点条件(3)的离散形式为 (11) 路径约束(4)的离散形式为 (12) (13) 作为多区间伪谱法的特例,全局配点法可以看作只包含1个子区间的多区间伪谱法,并且在该子区间应用高阶多项式离散最优控制问题。 为了提高计算效率和优化精度,本文应用文献[10]给出的hp自适应节点细化技术在优化过程中调整子区间分布以及每个子区间内的节点数量。 假设一般形式的控制变量变化率约束为 (14) 式中:u(t)表示原始轨迹优化问题的控制变量;rL和rU分别为控制变量变化率的下限和上限。 目前常用的处理方法是引入实际控制变量的导数作为虚拟控制变量,从而将原始控制变量转换为状态变量,其变化规律满足以下状态方程 (15) 式中:σ(t)为引入的虚拟控制变量。方程(15)与原始动力学方程(2)组成扩展形式的微分方程组。 虚拟控制变量的边界约束如下 rL≤σ(t)≤rU (16) 如果实际控制变量存在初始约束和终端约束,可以直接通过如下方式施加约束 u(t0)=u0,u(tf)=uf (17) 式中:u0和uf分别为控制变量的初值和终值。 这种引入控制变量导数作为虚拟控制变量的处理方法虽然简单,但是会带来一些问题。一方面,引入了新状态变量,显然增加了状态变量和状态方程的个数,进而增加了NLP的约束和优化变量的个数。尽管方程是线性微分方程,但是其离散形式是非线性的(与初始时间t0和终端时间tf存在耦合)。另一方面,方程为线性微分方程,容易产生奇异弧进而引起虚拟控制变量振荡甚至发散。这两方面原因都会增加NLP的求解难度和计算量。 为了克服上述控制变量斜率约束处理方法的弊端,本文引入有限差分法对约束进行离散 (18) 式中:uk=u(τk); Δτk=τk+1-τk。对其进行变换和整理,可以得到如下两个不等式约束 0≤uk+1-uk-[Δτk(tf-t0)]rL (19) 0≥uk+1-uk-[Δτk(tf-t0)]rU (20) 将其进一步整理成标准形式得到 uk-uk+1-ΔτkrLt0+ΔτkrLt0≤0 (21) -uk+uk+1+ΔτkrUt0-ΔτkrUtf≤0 (22) 对于控制变量的初始约束和终端约束,可以直接通过以下方式进行限制 u(τ0)=u0,u(τf)=uf (23) 式中:u0和uf分别为控制变量的初值和终值。 方程(21)、(22)和(23)全部为线性约束(离散控制变量、初始时间和终端时间的线性函数),其特点是一阶偏导数为常数、二阶偏导数为零,在求解NLP时不需要在每步迭代中反复计算偏导数,因而不会明显增加计算量。在方程(9)-(13)描述的传统伪谱轨迹法的基础上,增加方程(21)、(22)和(23)描述的控制变量变化率约束,即可得到考虑控制变量变化率约束的轨迹优化方法。图1给出该方法的流程图。相对于传统伪谱法,在非线性规划、归一化处理和求解器模块需要扩展以考虑控制变量变化率约束,在稀疏型分析和偏导数计算模块需要考虑控制变量变化率约束的常值偏导数,其它模块相同。 图1 带有控制量变化率约束的轨迹优化方法流程图Fig.1 Procedure of trajectory optimization method with the constraint on the change rate of control variables 本节采用两个轨迹优化算例展示本文方法的有效性,并与GPOPS软件进行了对比。其中,计算平台为桌面计算机,处理器为Intel Core i3-12100 3.3 GHz,内存为DDR4 8 GB,操作系统为Windows 11,编程语言为MATLAB 2017a。采用SNOPT求解NLP,采用稀疏有限差分法[15]提供一阶偏导数。文中给出的优化耗时为10次运行的平均耗时。 本算例优化空空导弹的攻角和推力脉冲时间间隔,使得导弹飞行时间最短或者射程最大。在纵向剖面内,描述导弹质心运行的微分方程组为 (24) 式中:x为水平位置;h为飞行高度;v为飞行速度;γ为航迹角;m为质量;T为发动机推力,Isp为燃料比冲,g0为海平面重力加速度;L和D分别为升力和阻力;α为攻角,为需要优化的控制变量。 升力和阻力表达式如下: (25) 式中:ρ为大气密度;Sref为气动参考面积;CL和CD分别为升力系数和阻力系数;Ma为马赫数。表1给出升力系数和阻力系数随马赫数和攻角的变化特性,其中参考面积Sref=0.02488 m2。该气动力数据是通过对美国空空导弹AIM-120C进行气动外形建模,然后采用CFD方法计算得出。与解析形式的气动数据相比,离散表格形式的气动数据在实际工程应用中更为常见,更具有代表性。 导弹采用双脉冲发动机提供推力,推力剖面如图2所示。其中,两个脉冲推力的大小和持续时间均为已知量,两个脉冲之间的时间间隔为设计变量,本文通过轨迹优化确定最优的时间间隔。 状态变量的初始条件为 (26) 表1 导弹的气动力系数Table 1 Aerodynamic coefficients of the missile 式中:r0,h0,v0,γ0和m0分别为状态变量的初值。 图2 双脉冲发动机推力剖面Fig.2 Thrust profile of the dual pulse engine 控制变量的初始条件为 α(t0)=α0 (27) 式中:α0为控制变量的初值。 为了充分发挥导弹的攻击效果,导弹命中目标时刻的速度需要满足如下约束 v(tf)≥vf (28) 式中:tf为终端时刻;vf为最低攻击速度。 导弹的终端高度为目标高度,即 h(tf)=hf (29) 式中:hf为命中点处导弹的高度要求。 控制变量攻角的变化范围约束如下: αmin≤α(t)≤αmax (30) 式中:αmin和αmax分别为攻角的下限和上限。 攻角的变化率需要满足如下约束 (31) 式中:umin和umax分别为攻角变化率的下限和上限。 为了防止导弹速度过大带来严重的气动加热问题,需要对导弹的飞行速度进行约束,即 Ma(t)≤Mamax (32) 式中:Mamax为允许的最大飞行马赫数。 本节研究两类不同目标函数的轨迹优化问题。第一类为最短时间轨迹优化问题(简记为P1),即导弹飞行的时间最短,目标函数为 minJ2=tf (33) 对于P1问题,通常还需要限定射程,即 x(tf)=xf (34) 式中:xf为导弹的射程要求。 本节研究的第二类轨迹优化问题为最大射程问题(简记为P2),目标函数为 minJ2=-x(tf) (35) 该轨迹优化问题描述为:确定最优攻角α(t)和脉冲时间间隔tg,使得目标函数(33)或者(35)最小化,并且满足动力学方程组(24),初始条件(26)和(27),终端约束(28)和(29),路径约束(30)~(32)。 在射程给定的情况下,飞行时间更短意味着能够更快地击中目标,因而P1问题具有工程实际价值。本文首先对P1问题进行仿真。根据双脉冲发动机的工作特性,空空导弹轨迹优化问题分为4段,分别为:第1脉冲工作段,脉冲间隔段,第2脉冲工作段,以及无动力滑翔段。采用的仿真参数为:r0=0 m,h0=6000 m,v0=400 m/s,γ0=0,m0=157 kg,α0=0,αmin=-15°,αmax=15°,umin=-2 (°)/s,umax=2 (°)/s,Mαmax=4.6,hf=6000 m,vf=600 m/s,xf=80000 m,T1=22775 N,T2=18980 N,t1=3.5 s,t2=4.0 s,Isp=247.23 s,g0=9.80665 m/s2。其中,攻角变化率参照文献[13]设置(文献[13]给出的攻角变化率为1 (°)/s,本文将其适当放大至2 (°)/s。虽然目前工程上允许设置更大的攻角变化率,但是变化缓和的攻角显然更容易跟踪。攻角变化率约束值越大,意味着攻角变化率约束越宽松(在极限情况下,攻角变化率为无穷大意味着攻角变化率实际上不受约束);攻角变化率约束值越小,更能体现出攻角变化率约束的影响。对于本文方法,不同的攻角变化率约束值对于展示方法的功能没有本质影响。 作为对比,本文首先采用开源软件GPOPS求解该问题。由于GPOPS不能直接施加控制变量初值和变化率约束,需要引入攻角导数作为虚拟控制变量,将攻角转换为状态变量。图3给出GPOPS优化的虚拟控制变量(攻角导数)和作为状态变量解算出的攻角随时间变化曲线。其中h方法为多区间伪谱法(采用均匀分布的子区间,每个子区间包含4个离散节点),p方法为全局伪谱法,即单区间伪谱法,hp方法为采用hp节点自适应方法调整节点分布的多区间伪谱法。对于h方法和p方法,各段轨迹采用的配点数目依次为12, 12, 12和32。对于hp方法,节点数目由节点细化算法迭代确定。可见,无论采用何种离散节点分布方式,GPOPS优化的虚拟控制变量(攻角导数)都发生了明显的振荡,并且在轨迹最右端的值超出了允许的变化范围,不是可行解。尽管如此,在GPOPS中作为状态变量的攻角没有表现出明显振荡,只是在轨迹最右端存在一定程度的振荡。但是对于GPOPS而言,虚拟控制变量在求解过程中被当作实际控制变量,是需要优化算法通过迭代求解的控制变量,该变量振荡会导致NLP收敛缓慢,甚至收敛困难乃至不收敛,由此带来的影响是增加优化耗时,降低了方法的可靠性。 图3 GPOPS优化的P1问题的控制变量Fig.3 Control solution to P1 using GPOPS 图4给出采用本文方法处理斜率约束时优化的攻角随时间变化曲线。其中,h方法和p方法的离散点分布方式和数量与GPOPS相同,hp方法的离散点数量和分布方式由节点细化算法[10]确定。可见,无论采用何种离散点分布方式,本文方法优化的攻角都不发生振荡。图5给出本文优化的离散轨迹和数值积分轨迹的对比,采用的离散点为hp自适应节点。可见,离散轨迹和数值积分轨迹非常一致,说明了优化精度高。从图5还可以看出,本文方法优化的终端高度、射程和飞行马赫数都严格满足约束要求。导弹飞行80 km需要的最短飞行时间为82.67 s,双脉冲推力的最佳时间间隔为6.35 s。 对比本文方法和GPOPS软件可知:GPOPS软件为了施加控制变量变化率约束,需要引入虚拟控制变量作为控制变量,而且在迭代求解过程中虚拟控制变量会振荡;本文方法不需要引入虚拟控制变量,因而避免了虚拟控制变量振荡问题,更容易收敛,能够减少优化耗时,可靠性更高(因为振荡有可能会导致不收敛)。表2给出本文方法与GPOPS的优化结果对比。可见,本文方法优化耗时明显少于GPOPS,对于不同的离散点分布方式,本文方法的优化耗时约为GPOPS的1/4~1/5。在目标函数和终端误差方面,本文方法和GPOPS没有明显差异。其中,终端误差定义为离散轨迹与积分轨迹在终端时刻的差异,Δr表示位置误差。在评估GPOPS结果的终端误差时,由于图3(a)所示的攻角导数振荡严重,据此积分带有方程(15)的扩展动力学系统会导致终端误差过大。考虑到方程(15)只与攻角直接相关,与其它方程的关系是通过攻角间接联系的,本文直接采用图3(b)所示的GPOPS优化的攻角作为控制输入,积分方程(24)所示的动力学方程组评估GPOPS结果的终端误差。对于该算例,GPOPS结果的攻角导数振荡并没有引起明显的攻角振荡,因而不影响其它状态方程的离散误差。对于求解器而言,控制变量振荡意味着收敛性差,增加了优化耗时。 图4 本文方法优化的P1问题的控制变量Fig.4 Control solution to P1using the proposed method 图5 本文方法优化的P1问题的状态变量Fig.5 State solution to P1 using the proposed method 表2 本文方法与GPOPS的优化结果对比Table 2 Comparison of results obtained using GPOPS and the proposed method 在导弹概念设计和方案论证阶段,最大射程是一个重要性能指标。对于P2问题,仿真条件与P1问题相同(需要移除射程约束)。同样为了对比,本文首先采用GPOPS软件求解该问题。为了施加攻角变化率约束,GPOPS需要引入虚拟控制变量(攻角导数)作为控制变量。图6给出采用不同分布方式的离散点时GPOPS优化的攻角导数和攻角随时间变化曲线。可见,无论采用何种离散点分布方式,虚拟控制变量(攻角导数)都发生了明显振荡,并且在轨迹最右端超出了限定的变化率约束范围。这些特性与求解P1问题时相同,进一步验证了GPOPS通过引入虚拟控制变量施加斜率约束容易发生振荡是一种普遍现象而非特例。因为描述攻角变化率的微分方程是线性微分方程,从最优控制的角度而言容易产生奇异弧进而引起攻角振荡甚至发散,Betts[5]在其专著中对于这一问题进行了论述。 图7为在不同离散节点分布情况下采用本文方法求解该问题得到的最优攻角随时间变化曲线。以其中的hp节点为例,导弹的最大射程为100.24 km,双脉冲推力的最佳时间间隔为6.63 s。 对比图6和图7可知,本文方法优化的攻角随时间变化更加光滑,其变化率严格满足约束要求,在轨迹末端也不发生突变。更重要的是,本文方法直接以攻角作为控制变量,能够直接施加攻角变化率约束,而GPOPS为了施加攻角变化率约束,需要引入虚拟控制变量(攻角导数)作为控制变量,在迭代求解过程中面临着虚拟控制变量振荡问题。这些因素使得本文方法得到的NLP规模更小,而且避免了GPOPS面临的虚拟控制变量振荡问题,计算量更小,收敛速度更快,可靠性更高。以采用hp节点为例,GPOPS求解P2问题耗时11.65 s,本文方法求解该问题耗时2.24 s,约为GPOPS的1/5。在轨迹终端精度方面,本文方法与GPOPS没有明显差异。这些特性与求解P1问题时类似。 图6 GPOPS优化的P2问题的控制变量Fig.6 Control solution to P2 using GPOPS 图7 本文方法求解的P2问题的控制变量Fig.7 Control solution to P2 using the proposed method 临近空间高超声速滑翔飞行器[16]在快速打击领域具有重要应用价值。参数化剖面控制由于简单、工程上容易实现,近年来逐渐受到重视[17]。本节研究基于参数化剖面控制的滑翔轨迹优化问题。 如图1所示,临近空间高超声速滑翔轨迹的飞行剖面可分成3段:第1段从起始点G0下滑到G1点,第2段从G1点持续滑翔到G2点(滑翔高度在hmin和hmax之间),第3段从G2点持续到G3点。假设每段攻角为常值参数,那么总共有3个参数。本文的参数化剖面优化就是对每段轨迹的攻角进行优化。由于攻角为常数意味着攻角变化率为0,因而本文建立的带有控制变量变化率约束的轨迹优化方法通过施加攻角变化率约束可以求解该问题。 图8 分段常值攻角飞行剖面示意图Fig.8 Sketch of sectional constant angle of attack profile 在二维纵向平面内,描述临近空间高超声速滑翔飞行器质心运动的微分方程组为 (36) 式中:r是飞行器距地心距离;θ是射程角;v是飞行器速度;γ是航迹角;m是飞行器的质量;g是重力加速度,g=μ/r2,μ是地球引力常数;L和D分别为升力和阻力,定义与前述P1问题中相同。 再入滑翔轨迹的初始条件为 (37) 式中:t0为初始时间;h0,θ0,v0,γ0和m0分别为状态变量的初值;高度h=r-Re,Re为地球半径。 为了命中定点目标,终端条件为 h(tf)=hf,θ(tf)=θf (38) 式中:tf为终端时间;hf和θf分为目标位置坐标。 为了充分发挥武器的打击效果,命中点的速度大小和方向需要满足如下约束条件 v(tf)≥vf,γ(tf)≤γf (39) 式中:vf为和γf为终端速度大小和方向约束边界。 在轨迹的第2段,轨迹跳跃的高度范围需要满足如下约束(不包括初始段和末端下压段) hmin≤h(t)≤hmax (40) 由于每段轨迹的攻角参数均为常数,因而在每段内,攻角变化率需要满足如下约束 (41) 在最短时间内击中给定的目标显然具有重要实战意义。本文以时间最短为目标函数,即 J=tf (42) 临近空间高超声速滑翔轨迹优化问题(简记为P3)可描述为:求解3个常值攻角,使得目标函数(42)最小化,并且满足状态方程(36),初始条件(37),终端条件(38)和(39),路径约束(40)和(41)。 对于P3问题,仿真参数为:h0=70000 m,θ0=0,v0=2835.9 m/s,γ0=0,m0=907.2 kg,hf=1000 m,θf=0.1570 rad,vf=1000 m/s,γf=-1.40 rad,hmin=35 km,hmax=45 km。飞行器的气动数据采用文献[16]给出的CAV气动数据插值计算,大气密度模型采用美国1976版本标准大气模型插值计算。 图9给出本文方法优化的3段常值攻角,图10给出以常值攻角作为输入控制,采用数值积分方法得到的轨迹状态变量曲线。其中,终端射程、终端速度、终端航迹角以及第2段轨迹的飞行高度范围全部满足约束要求。可见,本文方法通过限制控制变量的变化率为0,实现了对攻角参数的优化。本算例优化耗时为0.31 s,最优目标函数即飞行器滑翔给定射程需要的最短时间为444.26 s。与连续变化的攻角相比,分段常值攻角方案的优势是更容易跟踪(实际工程应用时还需要考虑相邻常值攻角之间的连续过渡,本文暂未考虑这一细节)。 图11给出采用连续变化攻角方案优化的攻角和滑翔轨迹曲线。其中,最短飞行时间为432.09 s,比分段常值攻角方案减少12.17 s(2.74%)。由图11(a)可知,连续变化攻角方案的最优攻角曲线比较复杂,显然会增加制导跟踪的难度。由图11(b)可知,连续变化攻角方案的飞行轨迹与常值攻角方案的轨迹比较接近,说明了常值攻角方案的合理性。 图9 本文方法优化的P3问题的控制变量Fig.9 Control solution to P3 using the proposed method 图10 本文方法优化的P3问题的状态变量Fig.10 State solution to P3 using the proposed method 本文提出一种考虑控制变量变化率约束的轨迹优化方法。该方法在传统伪谱法的基础上,引入有限差分法将控制变量变化率约束转化为计算量较小的线性约束,然后采用非线性规划算法求解。该方法能够方便地施加控制变量变化率约束,避免了传统伪谱法为了施加控制变量变化率约束需要引入虚拟控制变量以及由此导致的虚拟控制变量振荡问题,因而该方法具有更好的性能。采用带有控制变量变化率约束的空空导弹轨迹优化问题和临近空间高超声速飞行器滑翔轨迹优化问题验证了方法的有效性。仿真结果表明,与引入控制量导数作为虚拟控制量的控制变量变化率约束处理方法相比,本文方法能够将轨迹优化效率提高大约5倍。在可靠性方面,该方法由于避免了传统方法引入虚拟控制变量导致的虚拟控制量振荡问题,更容易收敛,更加可靠。本文的研究工作拓展了伪谱法的功能。 图11 连续变化攻角剖面情况下P3问题的最优解Fig.11 Optimal solution to P3 using continuously varying control profile

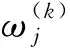

1.2 控制变量斜率约束


2 仿真算例与结果
2.1 双脉冲空空弹轨迹优化







2.2 临近空间滑翔轨迹优化

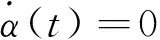


3 结 论