高考立体几何全国卷与浙江卷对比研究

朱成万 (浙江省杭州第十四中学 310006)

浙江省自2004年自主命题以来形成了自己的独特风格，浙江省教师的教学也形成了与之相应的思维定式和教学套路.2023年浙江高考将使用全国卷，全国卷与浙江卷相差很大，包括命题风格、题型、考查知识点的侧重等.因此，研究高考全国卷的特点对迎考复习具有现实意义.本文研究近10年(2012—2021年)高考立体几何部分试题(仅研究理科卷或文理合卷，其中全国卷共30份，浙江卷10份)，分析它们的异同，以期对教学有启发作用.

1 题量与分值对比分析

1.1 题量、分值统计表

1.2 题量、分值分析

从表1可以看到，两卷的题量与分值差别不大.全国卷中立体几何的分值以22分为主，约占总分(150分)的14%；题量以3题为主，都有1道大题和2道小题(选择或者填空题).浙江卷中立体几何的分值均为23分，约占总分(150分)的15%；题量为3题(1大题2小题).无论是浙江卷还是全国卷，立体几何均是高考必考内容，也是重点考查内容，在试卷中占有较大的比重，处于重要地位.

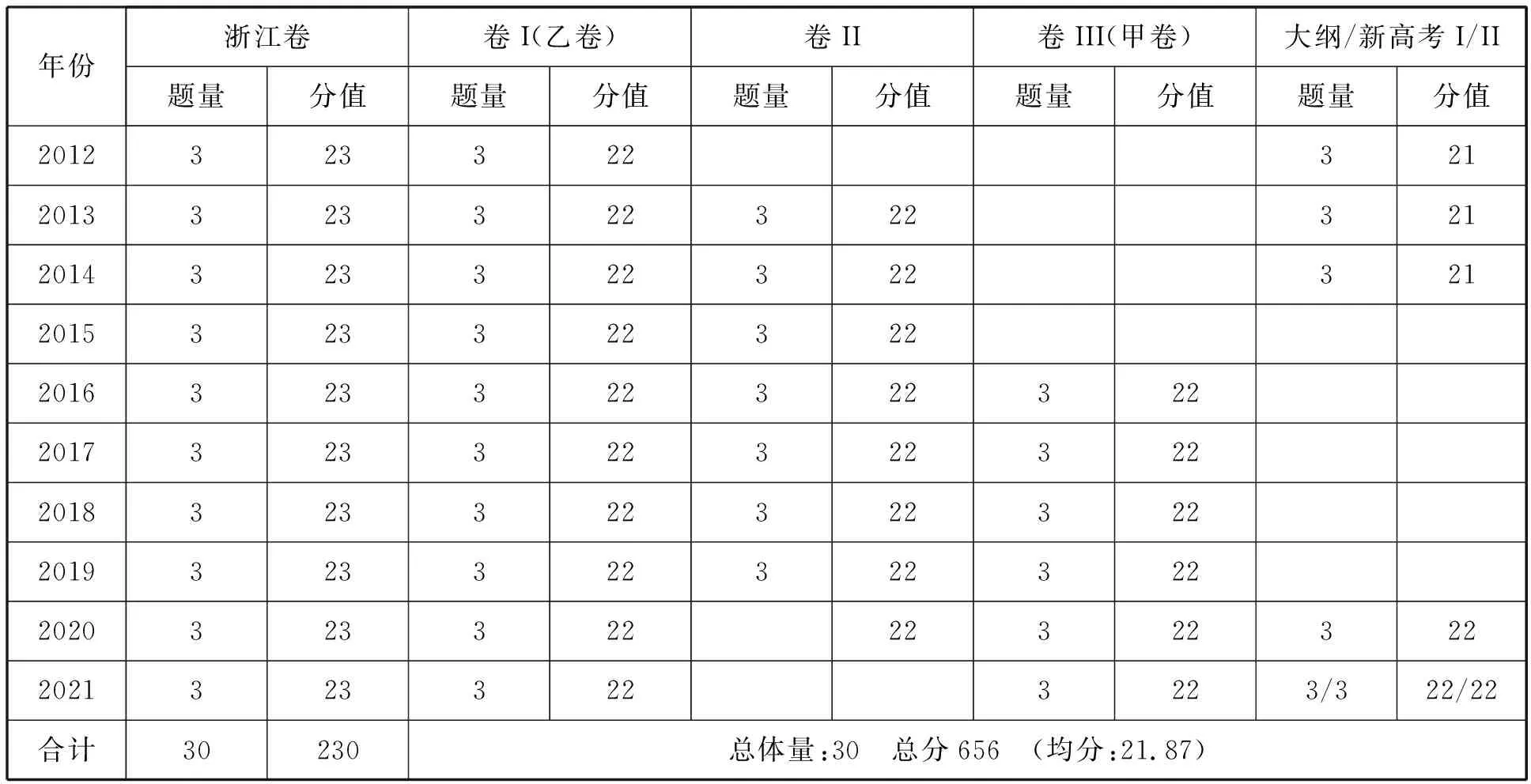
表1 2012—2021年高考浙江卷、全国卷立体几何题量、分值

2 考查内容对比与分析

2.1 考查内容统计

为了直观显示两卷的异同，根据表2画出相应的频率分布直方图(图1).

表2 2012—2021年高考全国卷、浙江卷立体几何知识点的考查次数

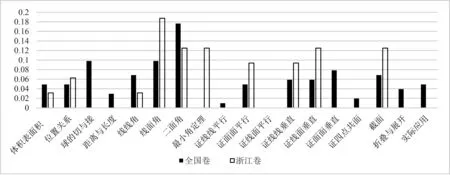
图1 2012—2021年高考全国卷、浙江卷立体几何考查内容频率分布直方图

2.2 考查内容对比分析

从表2和图1可以看出，对立体几何内容的考查，浙江卷与全国卷相差很大，主要体现在四个方面：

第一，浙江卷考点集中，全国卷考点分散.全国卷对内容的考查相对分散，几乎涉及立体几何的所有知识：几何体的体积与表面积、长度与距离、三类角度、平行与垂直关系、球的切与接、折叠与展开、数学文化与数学应用等.除了二面角及球的切与接，其他知识点分布比较均衡．相比而言，浙江卷中立体几何的考点相对集中，主要集中在线面角、二面角，线面垂直的判定，以及折叠与展开等几个问题．可见全国卷中立体几何的试题比浙江卷的试题视角更宽、层次更多．

第二，两卷同时反复考查的知识点较少.全国卷与浙江卷同时反复考查的知识点不多，只有线面角、二面角，线面平行、线线垂直、线面垂直等几个知识点.有许多内容是全国卷反复考查而浙江卷从不考，或者浙江卷反复考查而全国卷从不考.比如球的切与接，全国卷10年考查了10次，而浙江卷从未考查；再如最小角定理，浙江卷考查4次，而全国卷从未考查.

第三，“全国爱考二面角，浙江爱考线面角.”空间三类角(两异面直线夹角、线面角、二面角)是立体几何的核心内容，两卷对它们的考查差别很大.先看线面角，浙江卷考查了6次，而且连续6年(2016—2021年)浙江卷立体几何大题都是考查线面角，可见对浙江考生来说“线面角的地位比二面角更高”；再看二面角，浙江卷考查了4次(2012—2015年)，全国卷考查了18次，远远多于浙江卷.故称：“全国爱考二面角，浙江爱考线面角.”

第四，全国卷的创新力度比浙江卷强.浙江卷的题型基本固定，考查内容也基本固定，试题的创新主要体现在几何体结构上的变化.全国卷试题则不仅在几何体的结构上创新，在考点和题型上也不断出现新题，比如考查截面问题、证明四点共面以及数学文化与应用问题，而且还出现“多选题和结构不良试题”等.特别是2015年全国卷II第19题，需要画出截面四边形，该题无论是考查内容还是考查形式都让人耳目一新.

3 考查内容的理解

全国高考卷本着一核、四层、四翼的评价理念，注重学科特点，从学科思维价值和整体高度的角度出发，突出了数学知识的基础性和综合性[1]，以立体几何的重点知识和主干知识为主体，着意于数学知识运用的灵活性与创新性，将能力与素质融为一体，全面检测了学生的数学学科核心素养．下面分析全国高考卷是如何以立体几何为载体，通过“四翼”实现对学生“四层”的有效考查.

3.1 关注基础

全国卷注重对立体几何的基本概念和基本性质的考查，体现了知识立意，旨在检测学生的“学习掌握”情况．

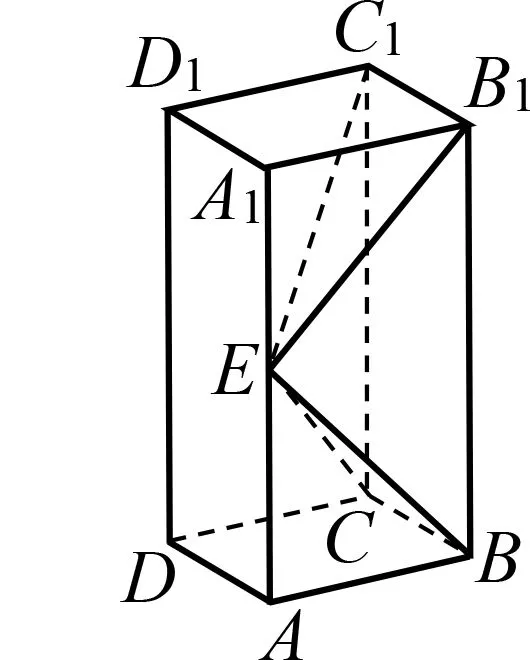
图2

例1(2019全国卷II理科题17)如图2，长方体ABCD-A1B1C1D1的底面ABCD是正方形，点E在棱AA1上，BE⊥EC1．

(1)证明：BE⊥平面EB1C1；

(2)若AE=A1E，求二面角B-EC-C1的正弦值．

评注 该题以长方体为载体，考查线面垂直关系和二面角的大小.该题给出了图形，考生可以用综合法求解，也可以直接建立空间直角坐标系，通过向量运算求解.该题背景常规、设问常规，解题方法也常规，只需掌握立体几何的基本知识就可以解答.高考通过该题检测学生对于立体几何基础知识的掌握情况，体现基础性.

3.2 强调综合

全国卷注重知识的综合，强调对知识的灵活应用．从学科内容选择的角度看，综合性要求以多项相互关联的活动组成的复杂情境作为载体，能够反映学科知识、能力内部的整合及其综合运用.[2]全国卷以基本知识为载体，考查基本能力，体现了能力立意，旨在检测学生灵活运用知识的能力．

例2(2019年全国卷I理科题12)已知三棱锥P-ABC的四个顶点在球O的球面上，PA=PB=PC，△ABC是边长为2的正三角形，E，F分别是PA，AB的中点，∠CEF=90°，则球O的体积为( ).

评注 该题以三棱锥的外接球问题为载体，主要考查了球的基本概念、三棱锥中元素的几何度量与位置关系判定，突出考查了球与三棱锥组合情境下的空间想象能力，同时着重考查学生的运算求解能力和应用能力.该题并未给出图形，如果考生画出图3，设PA=PB=PC=x，根据题中的位置关系和数量关系，用x表示△AEC各边长，然后运用余弦定理，则运算非常繁琐.如果能将三棱锥的外接球等价于正方体的外接球，画出图4，则问题迎刃而解.该题突出了对学生综合、灵活运用知识解决问题的能力的考查，对中学数学教学有积极的引导作用和很好的指导意义.

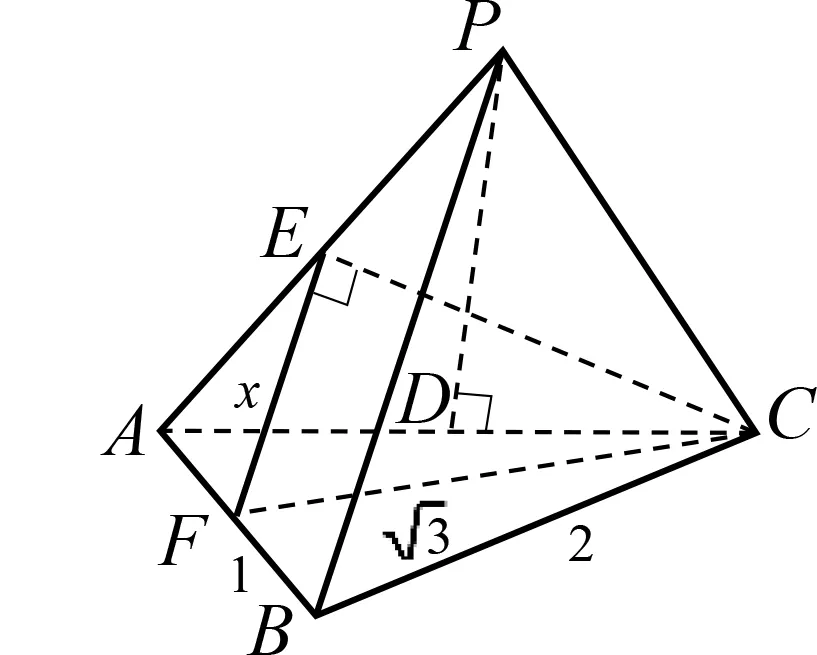
图3

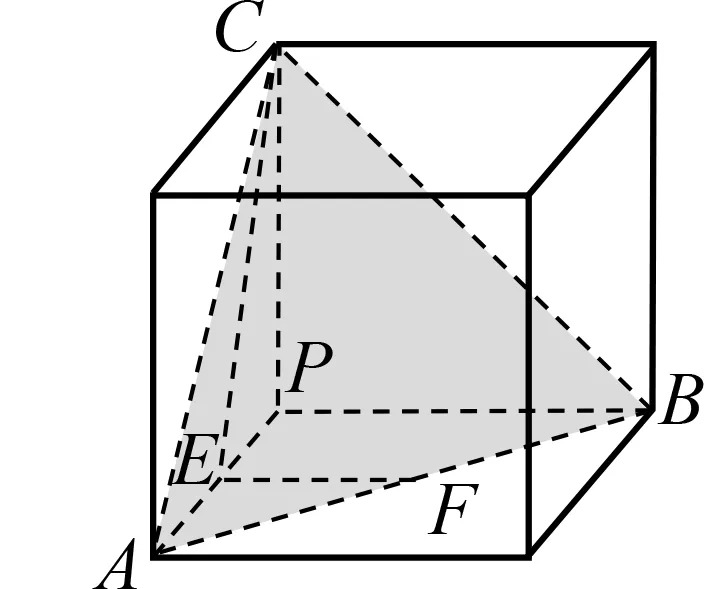
图4

3.3 重视应用

全国卷重视学以致用，试题联系生产生活中的实际问题，要求学生运用立体几何知识对实际问题进行分析与研究，进而解决问题，即强调立体几何在数学外部的综合应用．

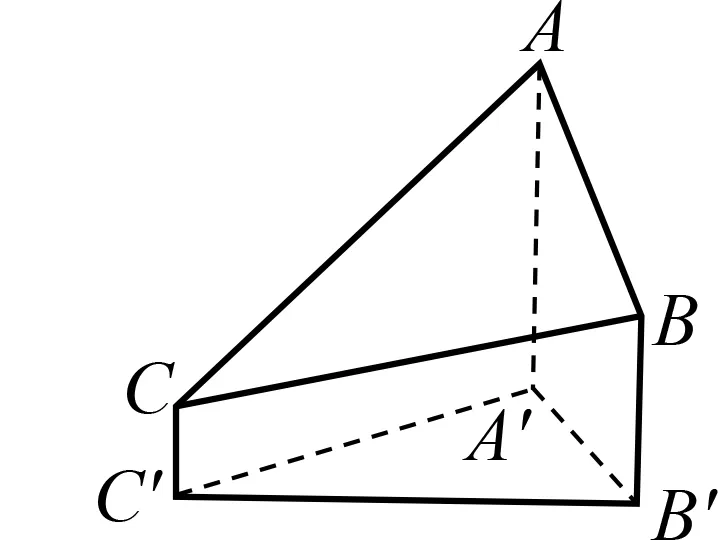
图5

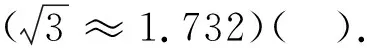
A.346 B.373 C.446 D.473

评注 本题以“三角高程测量法测量珠穆朗玛峰高程”为背景设计问题，要求学生利用立体几何的线面关系等构建模型，通过计算得出结论.这种试题情境真实，有利于培养学生的数学抽象、逻辑推理、直观想象等核心素养，同时渗透数学建模素养及数学思想方法的应用.

3.4 适度创新

全国卷注重适度创新，通过创设合理情境，设置新颖的试题呈现方式和设问方式，要求考生在新颖或陌生的情境中主动思考，完成开放性或探究性的任务，发现新问题、找到新规律、得出新结论，以检测考生的关键能力和必备品格．

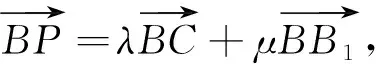
A.当λ=1时，△AB1P的周长为定值

B.当μ=1时，三棱锥P-A1BC的体积为定值

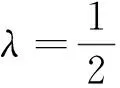
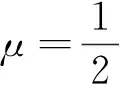
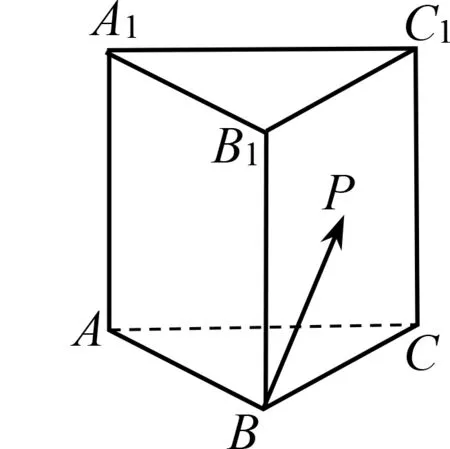
图6

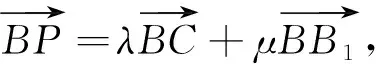
4 教学建议

4.1 聚焦全国卷，改变教学思维定式

从以上分析可知，浙江卷与全国卷差别很大.浙江教师如果仍以浙江卷命题规律组织教学，那就很难应对将来全国卷高考.比如浙江卷反复考查最小角定理，这类题目难度较大，学生需要较多的时间才能掌握，但是全国卷从不考，如果教师按照以往的思维定式，仍在该问题上花大力气，那是费时、费力且效果不佳.再比如，“球的切与接”也是一个较难的问题，学生需要一定的训练才能掌握.该内容全国卷年年考，但浙江卷从不考.如果教师还是按照之前应对浙江卷的思路，不涉及该内容，那么学生在未来高考遇到该问题，一定会手足无措.因此，浙江教师要以全国卷为导向，教学与复习才有针对性，才能在未来的高考中取得好成绩.

4.2 聚焦核心知识，形成空间观念

高考对基础知识的考查既全面又突出重点.对支撑学科知识的重要内容，占有较大的比例，构成试卷的主体.[3]立体几何是高中数学课程中的重要内容，在全国卷或浙江卷中都占有较高的分值.立体几何考查的核心是线面关系(特别是平行与垂直关系)和几何量计算(特别是空间三类角).对平行关系而言，线面平行的判定定理与性质定理是考查的重点，对垂直关系而言，线面垂直与面面垂直也是考查的重点，需要花大力气去训练.三类角的计算(特别是线面角与二面角)，无论是浙江卷还是全国卷都是重要考查内容.教学时在这些内容上下功夫，既是掌握立体几何核心内容、高考取得好成绩的必要条件，也是帮助学生形成空间观念、培养直观想象核心素养的良好载体.

4.3 不忘冷门知识点，复习要系统全面

高考要求“全面考查基础知识”，所以教学不仅要关注重点内容、关注热点问题，对冷门知识也不能遗漏.从表2可以看到，浙江卷考查的知识点相对集中，近10年集中在11个知识点上.对浙江卷而言，有许多知识是冷门(比如证明四点共面)，教师教学不重视，也很少给学生训练，将来使用全国卷，这些以往不重视、不关注的知识点都要重新重视起来.所以，对知识的复习要系统全面，到边到角，不留死角.

4.4 兼顾应用与创新，培养思维品质

素养导向的数学高考命题不断创新，其主要特点表现为人文性、趣味性、新颖性、生活性、开放性等.教学要适应高考的变化，在巩固基础知识的前提下要加强综合性、应用性问题的训练，增强对多选题、开放题的研究和训练.在核心素养统领下组织复习材料，侧重对立体几何知识的理解和应用，减少机械训练.通过掌握知识，提升思维品质，发展数学核心素养，才能以不变应万变，在高考中立于不败之地.