一道课本习题的溯源、破解与思考

张志刚 (山东省宁阳县复圣中学 271400)

徐章韬教授提出，理想的课堂是“学术”“技术”“艺术”三“术”交织的课堂．作为教师，其修为要能“上通数学、下达课堂”，能做“顶天立地”之事．然三“术”的发展具有序列性，先要解决一些“技术”问题，首先表现在教师能深刻研读教材，能看到教材背后的“微言要义”．课程教材承载的是传统成熟内容，是数学工作者集体智慧的结晶，不仅具备完整的学科知识体系，同时也是教师实施教学和学生学习的重要材料，而作为教材重要组成部分的习题理应置于显著的位置上．众多高考试题和竞赛试题都是从课本例题或习题出发，经过改编、综合、拓展、嫁接而来，具体表现为：课本例题、习题数据的变更，课本例题、习题条件的拓展，课本例题、习题背景的变换，课本例题、习题的应用等[1]．对典型习题的深度挖掘有利于我们发现问题的内涵和本质，“揭秘”题目背后的故事与历史渊源，概括归纳深藏其中的思维主线，以此为中心推而广之，可以收到以一敌百的良好成效．事实上，“小题深挖”“一题多法”“一题多变”“多题一法”充分体现了教学的简约性功能，能在尽可能短的时间内传播尽可能多的数学思想，对题海战术也是一种“反制”，历来都是我国习题课教学的宝贵经验，在继承与发展的道路上，我们应使其焕发新的生机．下面举例说明．

1 题目再现

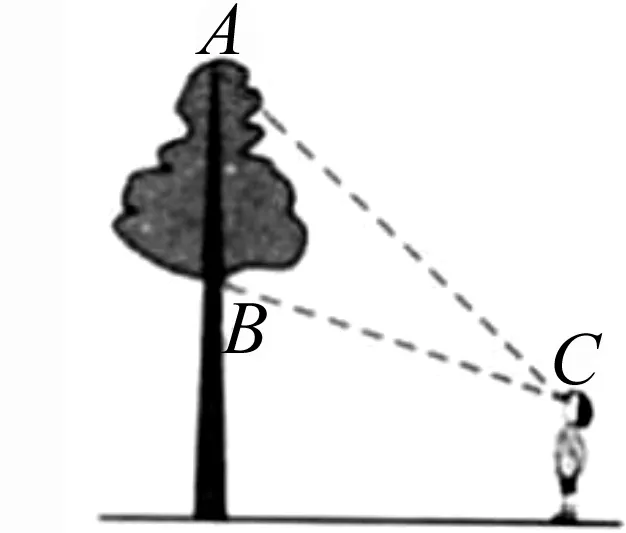
图1

普通高中课程标准试验教科书必修《数学5》(人教版2007年1月第3版，A版)第101页习题3.4B组第2题：如图1，树顶A离地面am，树上另一点B离地面bm，在离地面cm的C处看此树，离此树多远时视角最大？

2 问题剖析

2.1 问题探源

本题源于历史上经典的米勒问题．1471年，德国数学家、天文学家米勒(Johannes Miller)向诺德尔(Christian Roder)教授提出了一个有趣的问题：在地球表面的什么部位，一根垂直的悬杆呈现最长(即可视角最大)？上述最大视角问题因是米勒首先提出的，故被称为“米勒问题”．米勒问题广泛存在于各种实际问题中，例如探求欣赏一幅画的最佳角度、足球比赛最佳射门点等．

2.2 数学模型

历史上的米勒问题涉及的范围是三维空间．作为实际问题，我们首先要做的是根据实物背景抽象出简化的数学模型．相对于悬杆而言，地球的体积是相当大的，我们可视地球表面为平面，为了简化模型，同时忽略观察者身高对答案的影响，可以设观察者的身高为0，且悬杆在地面上的投影也为0，因为悬杆垂直于地面，所以距点O相同距离的点所得可视角是相同的(图2)．

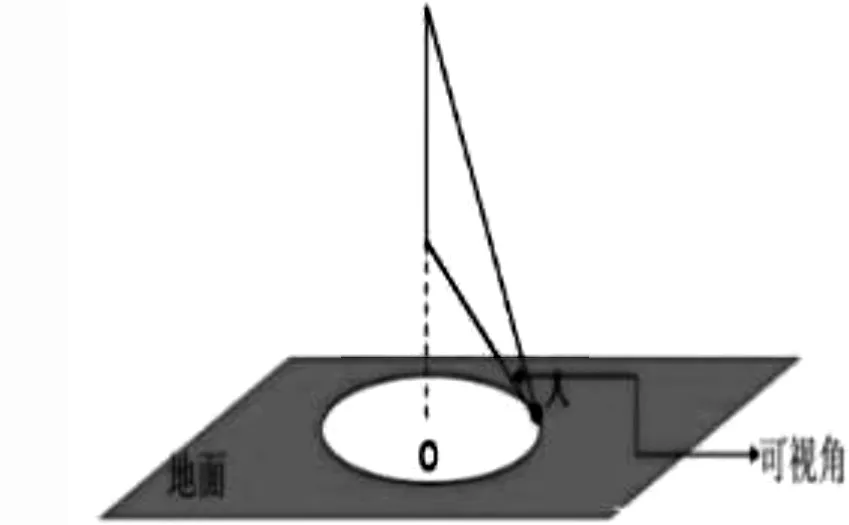
图2

2.3 问题转化

将上述模型一般化，可得到如下数学问题：如图3，设M,N是锐角∠AOB的一边OA上的两点，试在边OB上找一点P，使∠MPN最大．

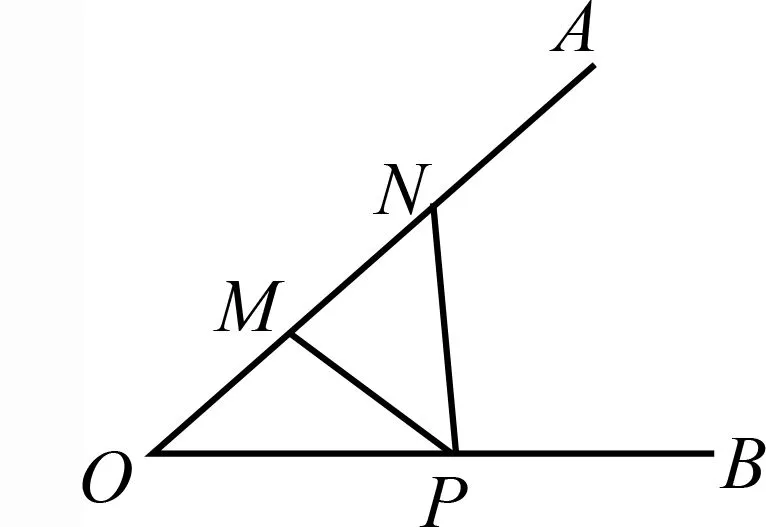
图3

对上述米勒问题，我们有如下重要结论，不妨称之为米勒定理：

米勒定理 设M,N是锐角∠AOB的一边OA上的两点，点P是射线OB上异于点O的一个动点，则当且仅当△MNP的外接圆与射线OB相切于点P时，∠MPN最大．

证明如图4，在射线OB上任取异于P的一点P′，连结MP′,NP′,NP′与圆相交于点C，易知∠MCN>∠NP′M．又因为∠MCN=∠MPN,所以∠MPN>∠MP′N.得证．

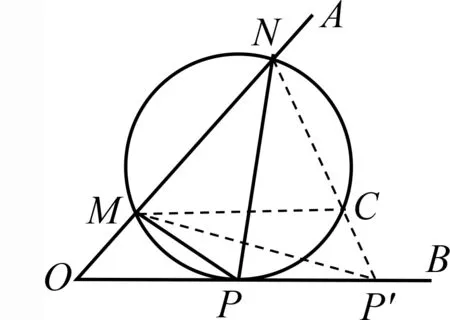
图4

3 问题解答

3.1 几何视角

解法1由圆的几何性质探求张角最大值.

如图5，DE是过点C且垂直于AB的直线，D为垂足．当DE与过点A,B的圆相切时，切点记为C，此时∠ACB=α最大．

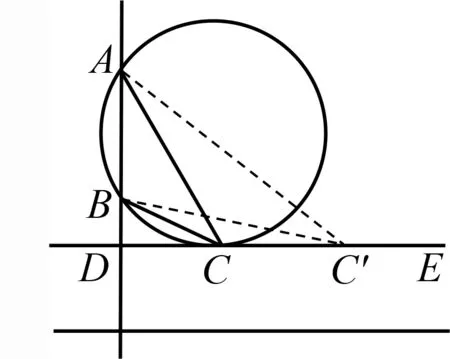
图5

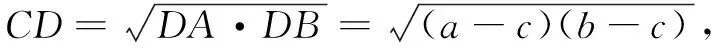
3.2 代数视角

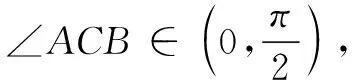
解法2探索锐角∠ACB正切的最大值.

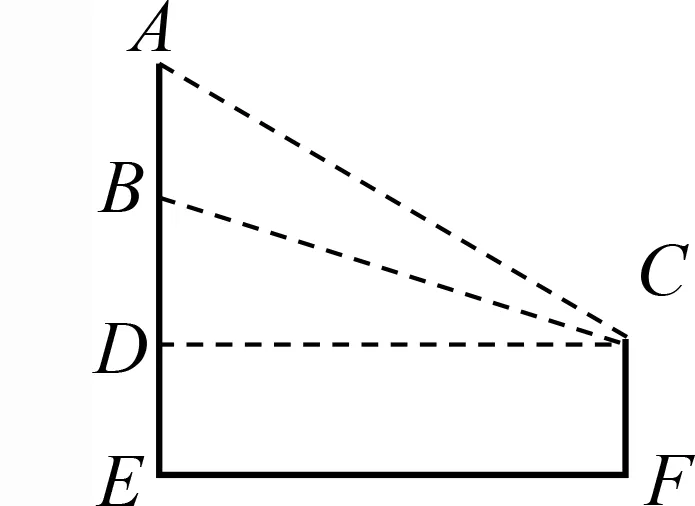
图6

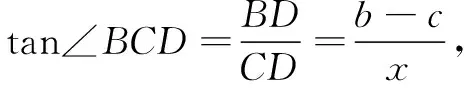
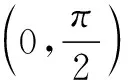
4 定理应用

以米勒问题为背景的最大张角问题在历年高考试题中屡见不鲜而又经久不衰，如1986年高考全国卷理科第5题、2005年高考浙江卷理科第17题、2010年高考江苏卷第17题等，若能从题设中挖掘、识别出隐含的米勒问题模型，将有效地突破思维瓶颈，大幅减少运算量，降低思维难度，从而使问题顺利获解．倘若无法及时提取该模型，很容易成为考生难以逾越的一道鸿沟．值得关注的是，米勒问题在竞赛数学中也频频亮相，需要引起足够的重视.下面列举几例．

题1(2004年全国高中数学联赛第12题)在平面直角坐标系xOy中，给定点M(-1,2),N(1,4)，点P在x轴上移动，当∠MPN取最大值时，点P的横坐标为．(参考答案：1)

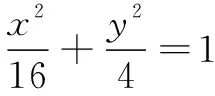
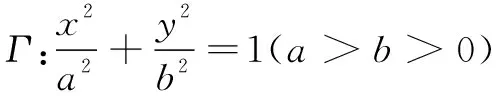
5 核心素养价值思考

从以上分析可以看出，米勒问题内蕴丰富，其解决过程需要直观想象、数学建模、数学运算、逻辑推理等核心素养，具有较高的挖掘价值．而直观想象素养是借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形来理解和解决数学问题的素养．主要包括：借助空间形式认识事物的位置关系、形态与运动规律；利用图形描述、分析问题；建立数与形的联系，构建数学问题的直观模型，探索解决问题的思路．[2]直观想象是发现和提出问题、分析和解决问题的重要手段．在数学研究的探索中，通过运用直观手段以及借助直观展开想象从而发现结论、作出猜想的例子比比皆是．直观想象在数学活动中是探索和形成论证思路、进行数学推理、构建抽象结构的思维基础．史宁中教授在《普通高中数学课程标准(2017年版2020年修订)解读》中提出的案例5-9本质上也是典型的米勒问题，他还以此为例说明了直观想象素养的三个水平．

案例5-9足球场上竖立一个电影屏幕，屏幕高为L，底部距离地面为H．设一人站在足球场上，眼睛距离地面高度为h，r=H-h>0．问：此人应该站在足球场上何处观看电影，眼睛观察屏幕上下沿形成的视角最大？

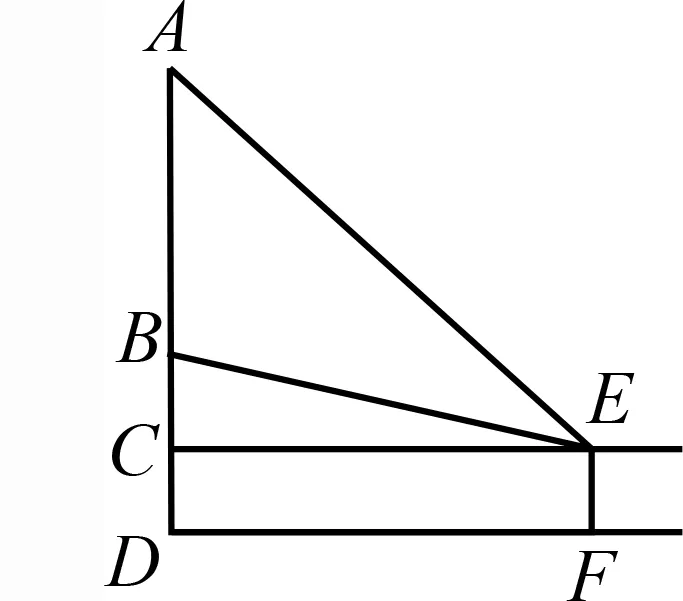
图7

用竖直的线段AB表示屏幕,用EF表示站立的人,E点为眼睛的位置，观察屏幕的上、下沿，形成视角θ=∠AEB，画出平面图(图7)．学生能描述和表达数学问题：设AB=L,BD=H,CD=EF=h，求点F的位置，使得视角θ最大．如此，学生能够建立事物的几何图形，体会图形和数量的关系，即达到了水平一的标准．

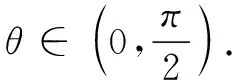
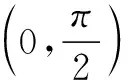
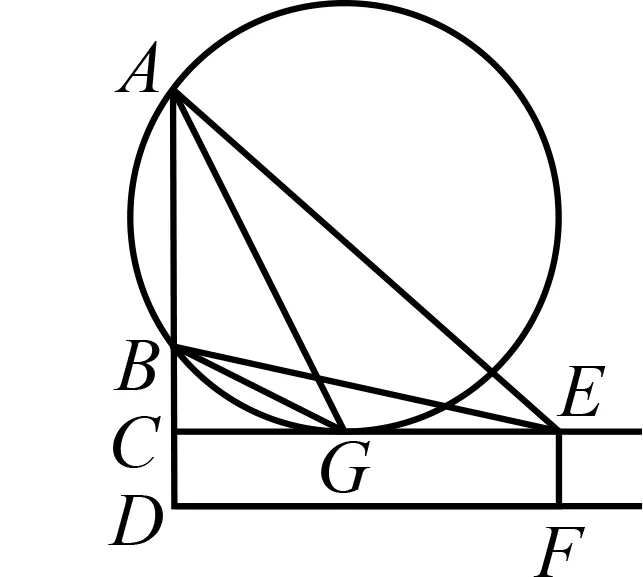
图8

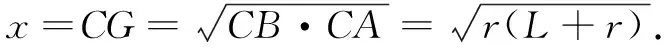
课程标准指出，直观想象主要表现为以下四点：建立数与形的联系，利用几何图形描述问题，借助几何直观理解问题，运用空间想象认识事物．米勒问题的解决过程是直观想象素养的完美演绎，是数形结合、转化与化归、函数与方程等数学思想应用的集中体现，是不可多得的训练素材和载体，极具教育价值．