基于SSA-RELM的S Zorb装置在线产品预测及多目标操作优化分析

邵珠林， 曹萃文

(华东理工大学 能源化工过程智能制造教育部重点实验室，上海 200237)

随着时代的进步，各国越来越重视经济发展与环境保护之间的平衡。汽车尾气的排放是环境污染的一大关键因素，汽车尾气中含有的硫氧化物和氮氧化物等有害成分进一步加剧了大气污染[1],这对汽油生产工艺提出了更高的要求，汽油吸附脱硫(S Zorb)技术能够有效脱除汽油中的硫化物，可使成品油的硫质量分数控制在10 μg/g以内。因此，对S Zorb装置进行全流程机理建模和多个产品指标操作优化，对指导工业生产和环境保护具有重要的意义。

S Zorb技术作为一种成熟的脱硫工艺，具有氢耗少、脱硫深度高和辛烷值损失低的优点，已在中国多个炼油厂使用。一方面，S Zorb装置的研究集中于故障的诊断分析：朱云霞等[2]提出了FCC汽油直进装置、再生风线改造和增加闭锁料斗的辅助硫化等措施，解决了中国石化燕山石化分公司S Zorb装置运行初期出现的换热器积垢和吸附剂结块问题。另一方面集中在吸附脱硫反应的机理研究：Bezverkhyy等[3]采用热重分析法对噻吩与Ni/ZnO的吸附脱硫反应进行了反应动力学的描述；邹亢等[4]研究了吸附剂对汽油辛烷值及脱硫能力的影响，并通过分子表征技术对吸附剂的物理性质和化学性质进行了考察。

化工过程建模方法主要分为机理建模和数据驱动建模。S Zorb装置机理建模的研究得到了广泛的开展。孟锐[5]针对镇海炼化S Zorb装置中低温热的利用问题，提出了新的换热网络，并利用Petro-Sim流程模拟软件进行测算，验证了该换热网络的有效性。蒋伟等[6]将构建了汽油辛烷值辛烷值损失预测模型，有效地预测了脱硫率和辛烷值等关键指标。李海明[7]建立了S Zorb装置中反应器和稳定塔的动力学模型、物料衡算模型和能量衡算模型，预测误差达到了5%。机器学习和人工智能技术的不断发展为化工过程建模提供了新的方法[8]。神经网络模型基于输入输出数据能够对非线性过程进行表征，同时基于BP算法的网络训练方法使得神经网络模型易于实现。但BP算法存在一定缺陷，会导致训练速率较慢且容易陷入局部最优，针对此问题，Huang等[9]提出了极限学习机(Extreme learning machine，ELM)模型，该模型具有单隐含层，随机产生输入层和隐含层的连接权重和阈值，在提高训练速率的同时保证了一定的预测精度。Deng等[10]针对ELM只考虑经验风险最小化和模型过拟合的问题，引入L2正则化项对ELM模型进行改进，提出了正则化极限学习机(Regularized extreme learning machine, RELM)模型。王改堂等[11]提出ELM岭回归的建模方法来预测延迟焦化粗汽油干点，当隐层节点为20时达到最优预测精度，预测均方误差为3.6729。与此同时，智能优化算法的引入对网络模型进一步优化，Cai等[12]提出基于粒子群优化算法的ELM模型对短期交通流量进行预测，通过引入粒子群搜索算法对网络权值和阈值进行优化，提升了预测精度。目前针对S Zorb装置数据驱动建模的研究还十分有限，笔者引入了一种新型的群智能算法——麻雀搜索算法[13]，该算法与现有的群智能算法相比具有很好的全局搜索能力和局部搜索能力，笔者基于该算法对正则化极限学习机进行改进，建立了高精度的产品指标预测模型。

在实际的生产过程中，炼油厂通常要兼顾多个工艺指标以保证产品质量，工艺指标之间往往是相互影响的，不同的操作变量对不同的指标影响程度也不尽相同。于晓栋等[14]利用Aspen Hysys进行常压塔静态模拟，以最大化产品收益和最小化装置能耗为优化目标，利用非支配排序遗传算法找到Pareto解集。焦云强[15]提出了炼油企业氢气系统的多目标设计策略，利用变权系数的加权法将多目标优化问题转化为单目标优化问题，根据Pareto最优前沿权衡投资成本和操作成本，给出优化后的设计方案。

为实现S Zorb装置产品指标的在线预测和多目标优化分析，笔者根据某炼油厂S Zorb装置的生产工艺和有限的过程数据，通过相关性分析选取得到10个操作变量。结合实际的工艺参数，建立了Aspen Plus的生产过程机理模型。然后对机理模型进行有效性检验和灵敏度分析，并建立SSA-RELM产品预测模型。最后将精制汽油流量、硫含量和氮含量作为优化目标，给出了不同分区下多目标在线操作优化方案。

1 S Zorb装置机理建模与数据采集

1.1 基于GBDT融合特征贡献度的相关性分析

在实际的化工过程当中，各变量之间具有高度的非线性和强耦合性，分析不同变量之间的相关性就变得十分复杂。梯度提升决策树(Gradient boosting decision tree, GBDT)是基于决策树模型的集成学习算法，因其具有较高精度，常被用于回归预测当中。Friedman[16]提出通过计算特征在每棵树上的平均贡献度来衡量特征的全局贡献度，结点在分裂时的均方误差损失值越大，特征的重要性越高。节点信息可以很好地反映操作变量对目标变量的贡献度，通过计算分裂节点的均方误差损失值就可以得到相应特征的贡献度，该计算方法能够充分地表征操作变量和目标变量之间的相关性。

某炼油厂DCS系统每隔6 min采样一次，共得到现场数据6720组，去除原始数据中的缺失值和错误值，处理后得到6527组数据。根据工艺手册，对24个主要操作变量进行相关性分析，分别建立24个操作变量与精制汽油产品流量和硫含量的GBDT模型，并根据节点信息计算各个特征对应的特征贡献度，通过等比例加权融合方法得到融合特征贡献度，融合特征度的大小反映了相关性的大小。各操作变量的融合特征贡献度如图1所示。

F1—3# Feed flowrate; F2—Hydronaphtha flowrate;T1—Heating furnace inlet temperature;T2—Hot separator temperature;p1—Reactor pressure; T3—Gasoline temperature;F10—Steam flowrate; T4—Cold separator temperature;T5—Gas outlet temperature; p2—Hot separator pressure;T6—Regeneration temperature; F4—Deoxygenated water flowrate;F5—Gas flowrate; L1—Hot separator liquid level;F6—Regenerator N2 flow; p3—Cold separator pressure;T7—Reactor temperature; F7—H2S flow;p4—Regeneration pressure; s1—Capacity of regenerator;p5—Tower top pressure; L2—Cold separator liquid level;F8—N2 flowrate; F9—2# Feed flowrate图1 基于GBDT融合特征贡献度Fig.1 Fusion feature contribution based on GBDT

在图1中,将24个操作变量的融合特征度按由大到小的顺序进行排序，从中选取10个具有较高特征贡献度的操作变量：3#进料流量(F1)、加氢石脑油进料(F2)、加热炉进口温度(T1)、热分温度(T2)、吸附脱硫反应器压力(p1)、产品汽油出装置温度(T3)、蒸汽进装置流量(F10)、冷分温度(T4)、干气出装置温度(T5)和热分压力(p2)。经计算，这10个操作变量的特征贡献度之和为0.975，所选操作变量能够充分反映对目标变量的贡献度。

1.2 基于Aspen Plus的S Zorb装置机理建模

S Zorb吸附脱硫工艺以催化裂化(FCC)汽油为原料，FCC汽油中的硫化物与Ni和ZnO所组成的吸附剂发生吸附脱硫反应，噻吩类化合物中的硫原子直接被吸附剂所吸收形成金属硫化物，反应后的吸附剂通过后续的吸附再生反应实现吸附剂的再生。王连山等[17]提出了38集总组分对物料进行表征，建立了可靠的连续重整装置的集总动力学模型。在此基础上，针对Aspen Plus机理模型，笔者采用42集总模型(烷烃19集总、烯烃10集总、芳烃5集总、硫化物6集总、氮化物2集总)对原料进行表征[18]，其中硫化物用噻吩硫、硫醚和硫醇进行表征，氮化物用喹啉和吡啶进行表征[19]。S Zorb装置主要分为3个单元：吸附脱硫单元、吸附剂再生单元和产品稳定单元。下面将结合图2依次对3个主要单元进行介绍。

(1)吸附脱硫单元：该单元的进料包括新氢进料(H2)、罐区补充进料(FCC-1)、2号罐区进料(FCC-2)、3号罐区进料(FCC-3)，以上进料经过加热炉预热进入到吸附脱硫反应器(Reactor)中，与吸附剂(Adsorb)发生吸附脱硫反应，同时反应器内还包含一定程度的烯烃加氢反应和烯烃加氢异构化反应。反应完成后，含硫吸附剂经阀门(V-1)进入到吸附剂再生单元。而气相物流经冷却器(COOL-1)进入热分罐(SEP-1)进行初次气-液两相的分离，液相进入产品稳定单元进行精馏，而气相物流经冷却器(COOL-2)再次换热后进入冷分罐(SEP-2)，进行第二次气-液分离，分离后的气相作为循环氢进行循环利用，液相经分离罐(B-2)脱水后进入产品稳定单元。

(2)吸附剂再生单元：在实际的生产过程中，吸附剂再生单元通过步序控制使脱硫反应器(Reactor)中的吸附剂保持一定活性，笔者建模时暂未考虑吸附剂活性变化的影响。吸附脱硫反应结束后，待生吸附剂中被吸附的硫原子主要以ZnS的形式存在，通过再生反应器中氧化反应重新得到具有吸附活性的ZnO，反应产生的烟气进入SRU硫磺回收系统进行处理。反应后的固体吸附剂中含有一定成分的NiO，继续在还原反应器(CONV-2)中完成Ni的还原，最终得到再生的吸附剂。

H2—New hydrogen feed; FCC-1, FCC-2, FCC-3—1#, 2#, 3# Fluid catalytic cracking gasoline; Adsorb—Adsorbent feed; Air—Air feed;CIR-H2, RE-H2—Circulating hydrogen; Naphtha—Hydrogenated naphtha; WW-1, WW-2—Waste water; Fuel-Gas—Emission of fuel gas;New-Adsorb—Regenerative adsorbent; Gas—Dry gas; Product—Refined gasoline; MIX-1, MIX-2, MIX-3, MIX-4, MIX-5, MIX-6—Mixer;HEAT-1—Heater; COOL-1, COOL-2, COOL-3, COOL-4, COOL-5, COOL-6—Cooler; SEP-1—Hot separator；SEP-2—Cold separator; SEP-3, SEP-4, SEP-5, SEP-6—Separator; Reactor—Adsorption desulfurization reactor;CONV-1, CONV-2—Regenerative reactor; B-2, B-1—Separator; T-1—Distillation tower; V-1, V-2—Valve图2 S Zorb工艺流程模拟Fig.2 Simulation of S Zorb process

(3)产品稳定单元：经过分离后的汽油与调合石脑油(FCC-4)混合进入精馏塔(T-1)，设定精馏塔的塔板数为30，汽油进料为第12塔板。经过精馏后得到精制汽油(Product),并排出干气(Gas)，建模过程中所涉及的参数均按照工艺手册的要求设定。

1.3 Aspen Plus模型的有效性检验与灵敏度分析

Aspen Plus模型计算收敛之后，利用实际数据对模型的有效性进行检验，保证后续生成扩展数据集的可靠性。针对1.1节中某炼油厂DCS系统的6527组实际有效数据，忽略掉测量变送装置和各反应器的反应因素等造成的时滞，利用随机抽样的方法从每日0—12时和12—24时各随机抽取1个样本点，共得到该月的56个测试样本。将精制汽油流量和精制汽油硫含量作为有效性检验的指标，对比仿真结果与实际数据，绘制仿真数据与现场数据的对比图像，同时计算2个有效性检验指标的均方误差MSE、平均绝对误差MAE。

图3为精制汽油流量和硫含量实际值与仿真值的比较。由于建立机理模型的过程中未考虑实际生产过程中的损耗，因此在图3仿真结果中预测值略大于实际值，但预测值的变化趋势与实际值的变化趋势保持一致，同时预测误差保持在一定的范围内。在精制汽油流量的误差计算结果中，MSE为6.747，MAE为6.612；在精制汽油硫含量的误差计算结果中，MSE为0.261，MAE为0.219。以上2个产品指标的验证结果证明了模型的有效性。

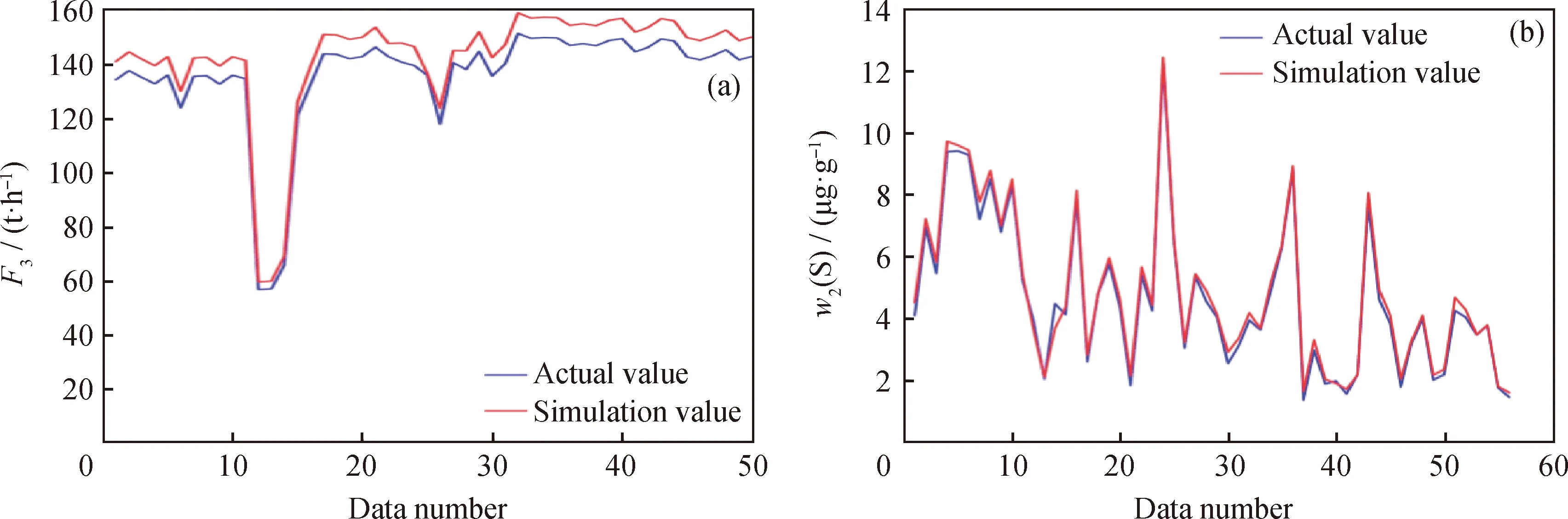
图3 精制汽油流量和硫含量实际值与仿真值的比较Fig.3 Comparison of actual and simulation data of refined gasoline flowrate and its sulfur content(a) Refined gasoline flowrate (F3); (b) Sulfur mass fraction (w2(S)) of refined gasoline

通过Aspen Plus机理模型进行灵敏度分析，对1.1节相关性分析得到的10个操作变量(3#进料流量、加氢石脑油进料、加热炉进口温度、热分温度、吸附脱硫反应器压力、产品汽油出装置温度、蒸汽进装置流量、冷分温度、干气出装置温度和热分压力)进行进一步的筛选，找到对于Aspen Plus模型灵敏度高的变量作为输入变量。将以上10个操作变量作为机理模型的自变量，计算当自变量数值波动1%时精制汽油流量和硫含量变化的百分比，通过该百分比的数值来反映机理模型对于自变量的灵敏度。经计算，精制汽油流量和硫含量对产品汽油出装置温度、吸附脱硫反应器压力和蒸汽进装置流量不敏感，灵敏度的计算值近似为零，因此选择其余7个操作变量为输入变量。

1.4 运行Aspen Plus模型扩充数据集

由于目前所掌握的现场数据较为有限，在一定时间段内的工况变化范围较小，为保证数据驱动建模过程中数据的完备性，运行机理模型对数据集进行扩充。考虑到在实际的生产过程中原料油的批次不同，原料油中含硫化合物变动较大，因此将进料油的硫含量纳入数据驱动建模的输入变量，结合1.3节灵敏度分析得到的7个输入变量，共计得到8个输入变量。

根据生产工艺的要求，各输入变量在允许的范围内取值，同时根据对该炼油厂实际有效的6527组DCS数据进行的统计,找到在常规工况下各个输入变量分布密集的区间和分布稀疏的区间。在分布密集的区间内选取较多的点，在分布稀疏的区间内选取较少的点。详细列出如下：原料油硫质量分数(410～450 μg/g，取值为{410，430，450})，3#进料流量(60000～90000 kg/h，取值为{70000，80000，90000})，干气出装置温度(不大于45 ℃，取值为{30.00，31.25，32.50，33.75，35.00，45.00})，热分温度(100～150 ℃，取值为{120，136，137，138，139，145})，冷分温度(不大于45 ℃，取值{30.0，32.5，35.0，37.5，40.0，45.0})，加氢石脑油进料(2000～5000 kg/h，取值为{2000，4000})，加热炉进口温度(380～440 ℃，取值为{418，421，424，427，430})，热分压力(1.9～2.9 MPa，取值为{2.300，2.325，2.350，2.375，2.400，2.800})。Aspen Plus机理模型的输出为：精制汽油质量流量(kg/h)、精制汽油硫质量分数(μg/g)和精制汽油氮质量分数(μg/g)，此3项为产品质量相关的指标。按照以上输入变量的取值运行Aspen Plus机理模型，得到111840组数据。扩展数据集如表1所示。

2 基于SSA-RELM的数据驱动建模

2.1 正则化极限学习机

极限学习机作为一种单隐层前馈神经网络，与BP网络模型相比，具有更快的训练速率，特别是在训练数据量大的情况下，具有明显的优势，适合在线的训练和多目标的预测。假设有一训练数据集S={(x1,y1),(x2,y2),…,(xl,yl)}，其中xi∈Rn表示n维输入，yi∈Rm表示m维输出，i=1,2,…,l，其中l为数据的个数。假设隐层神经元的个数为N，激活函数为G(x)的极限学习机可以表示为：

(1)

式(1)中：ωj是第j个神经元的输入权重；βj是第j个神经元的输出权重。式(1)可用矩阵表示为：

Y=H·β

(2)

式(2)中：H为隐含层的输出；β为隐含层与输出层的连接权值；Y为网络的输出。由于输入层到隐含层的权值和阈值可以随机赋值，则隐含层与输出层之间的连接权值可以通过式(3)求解得到：

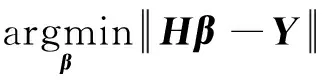
(3)

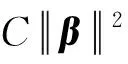
(4)

式(4)中，C为常数，求解得到式(4)的解为：

(5)

式(5)中,I为单位矩阵。

表1 扩展数据集Table 1 Extended database

在RELM的训练过程中，首先确定模型输入神经元的个数、输出神经元的个数和隐含层神经元的个数，然后随机初始化输入层到隐含层的权重和阈值，结合训练数据集计算β，最后利用训练好的RELM模型进行预测。

2.2 麻雀搜索算法

麻雀搜索算法是一种新型的群智能优化算法，该算法具有很好的局部搜索能力和全局搜索能力。通过与其他算法在收敛速率、精度和稳定性对比，麻雀搜索算法均有很好的表现[20]。

麻雀搜索算法中将种群个体分为发现者和追随者，发现者具有较高适应度的值，指引追随者的移动。但是一旦麻雀察觉到捕食者，就会移动到安全区域，每个追随者在发现最好的食物来源时都有机会成为发现者，算法主要包括发现者的更新过程、追随者位置的更新和反捕食位置的更新。发现者的位置更新公式如下：

(6)

(7)

式(7)中,Xworst为当前历史最差的位置；XP是发现者当前的最优位置；A为1×d维向量，向量元素随机赋值1或-1，A+=AT(AAT)-1；P为麻雀种群的数量，根据上式完成追随者的位置更新。为了防止陷入局部最优，提高全局搜索的能力，引入反捕食的策略。反捕食者的数目可以设定为种群数目的10%到20%，该群体的选择方式如下：

(8)

2.3 麻雀搜索算法优化正则化极限学习机

极限学习机在进行初始化时，输入层到隐含层的权值和阈值均为随机生成，这就很难保证极限学习机发挥最优的性能。针对这个问题，笔者提出了基于数据驱动SSA-RELM建模方法，在RELM模型的基础上引入麻雀搜索算法，使得每个麻雀个体中包含输入层带隐含层的连接权值信息和隐含层的阈值信息，通过寻找麻雀种群中最优个体来得到最优的网络权值和阈值，适应度函数用实际值和预测值的均方误差来表示，均方误差越小则个体的适应度越高。利用麻雀搜索算法得到的最优权值和阈值对RELM模型进行初始化，进而建立SSA-RELM的模型，算法步骤如下：

Step 1 将数据集划分为训练集和测试集，分别用于模型的训练和预测；

Step 2 设置麻雀搜索算法的超参数，如种群大小、最大迭代次数、预警值等，并对种群进行随机初始化；

Step 3 计算初始的个体适应度、当前最优适应度和最差适应度，并按照适应度对个体排序；

Step 4 按照2.2节公式依次进行发现者、追随者和反捕食者的位置更新；

Step 5 再次计算个体适应度、全局最优适应度和全局最差适应度；判断是否到达最优迭代次数，是则跳转Step 6，否则跳转Step 4；

Step 6 利用最优个体对RELM的权值和阈值进行初始化，利用训练数据集求解输出层连接权值β；

Step 7 使用训练好的模型进行多目标预测。

2.4 预测结果对比与分析

按照算法流程进行数据驱动建模，将扩充数据集进行随机划分，训练集数据占比80%，测试集数据占比20%。首先对麻雀搜索算法中的超参数进行设定，种群数量设置为50，个体的维度为1440，每个个体都包含输入层到隐含层的权重信息和隐含层的阈值信息，发现者数量设为群体数量的20%，最大迭代次数设置为100，个体每一维度的上界和下界分别取1和-1，使得网络的权值在[-1,1]之间选取。同时对RELM的网络结构进行初始化设定，输入层神经元的个数为8，分别表示3#进料流量、加氢石脑油流量、加热炉进口温度、热分温度、冷分温度、反应器压力、干气出装置温度和原料硫含量，隐含层神经元个数设为160，输出层神经元个数为3，分别表示精制汽油流量、氮含量和硫含量。分别按照2.3节建模过程建立RELM模型和SSA-RELM模型，并从测试集中随机抽取112组数据进行测试，2种模型的预测值与实际值的对比曲线和偏差曲线如图4～图9所示。对于图4、图6和图8 可知，实际值和预测值拟合效果越好说明精度越高；对于图5、图7和图9，曲线的波动幅度越小，说明越靠近偏差为0的水平线，预测结果越精确，反之曲线的波动幅度越大，预测结果越不精确。

F3—Refined gasoline flowrate图4 不同预测模型下精制汽油流量的预测值和实际值Fig.4 Predicted and actual data of refined gasoline flowrate with using different prediction models(a) RELM model; (b) SSA-RELM model

F3—Refined gasoline flowrate图5 不同预测模型下精制汽油流量预测偏差Fig.5 Difference of refined gasoline flowratewith using different prediction models

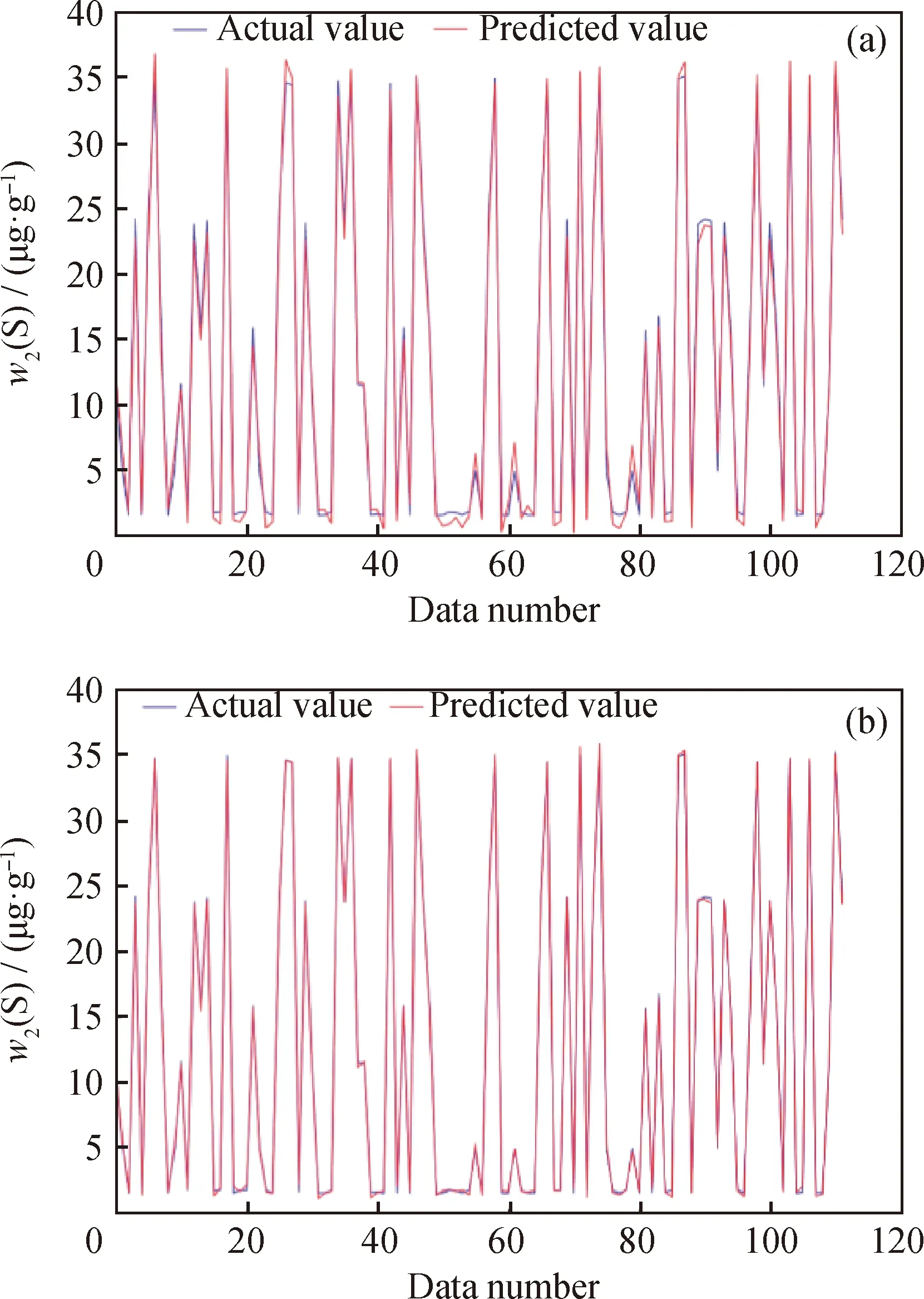
w2(S)—Sulfur mass fraction of refined gasoline图6 不同预测模型下精制汽油硫含量的预测值和实际值Fig.6 Predicted and actual sulfur content of refined gasolinewith using different prediction models(a) RELM model; (b) SSA-RELM model

由图5、图7和图9可以看出，对于3个指标的预测结果，改进后的SSA-RELM模型比RELM具有更高的预测精度。分别计算预测指标的均方误差MSE和平均绝对误差MAE，计算结果如表2所示。由表2可知，SSA-RELM模型在RELM模型的基础上进一步提升了预测精度。在实际的生产过程中，改进后的模型能够实现快速地多目标预测，为实际生产操作提供相应的指导，提高生产的稳定性和产品汽油的质量，增加炼油厂的经济效益。

w2(S)—Sulfur mass fraction of refined gasoline图7 不同预测模型下精制汽油硫含量预测偏差Fig.7 Difference of sulfur content of refined gasolinewith using different prediction models

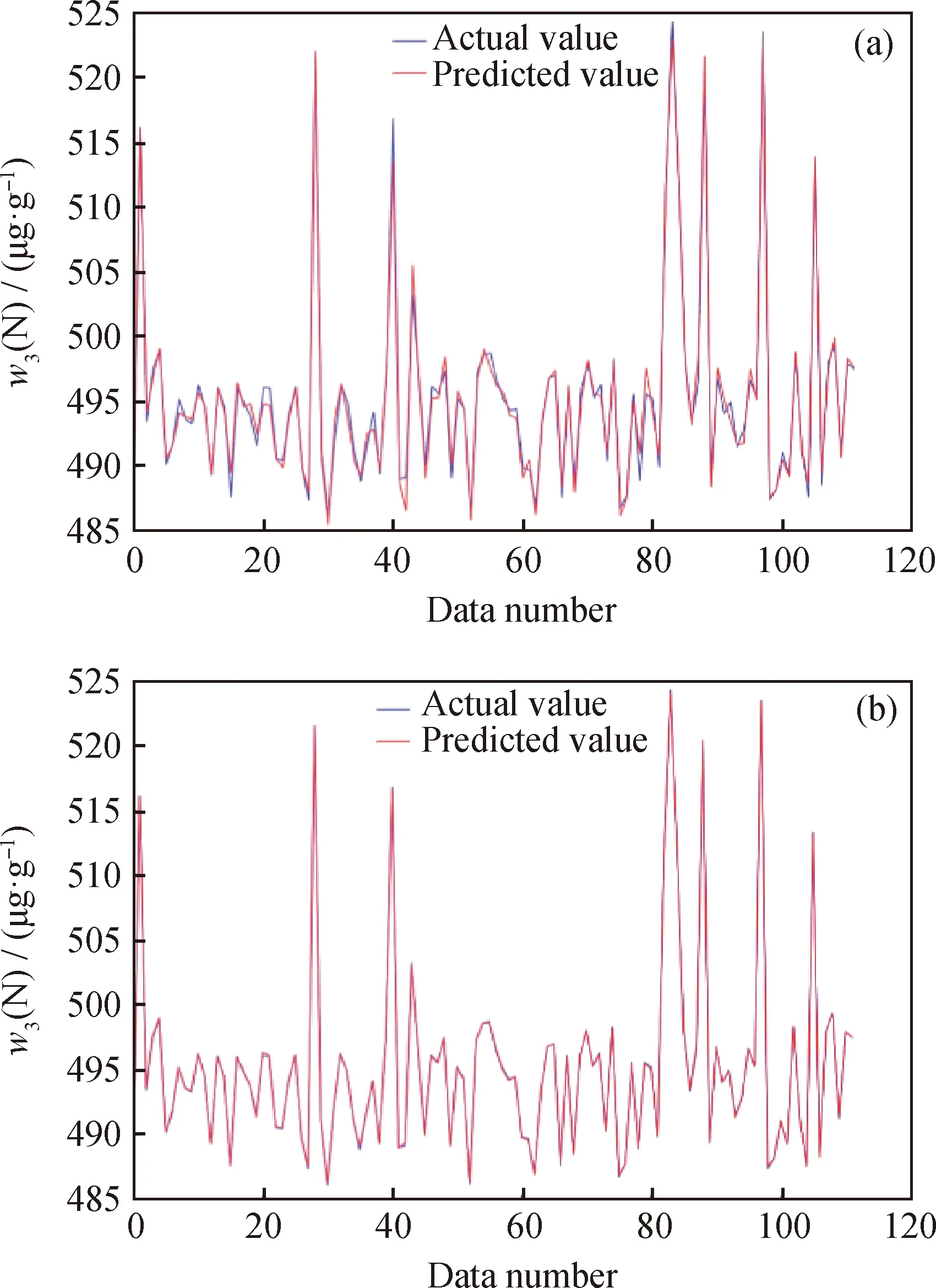
w3(N)—Nitrogen mass fraction of refined gasoline图8 不同预测模型下精制汽油氮含量的预测值和实际值Fig.8 Predicted and actual nitrogen content of refinedgasoline with using different prediction models(a) RELM model; (b) SSA-RELM model

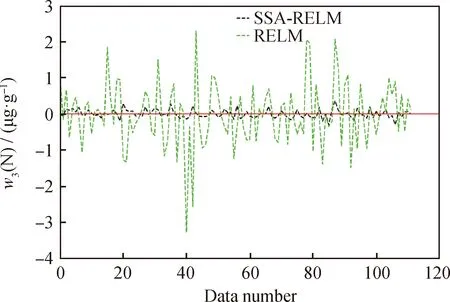
w3(N)—Nitrogen mass fraction of refined gasoline图9 不同预测模型下精制汽油氮含量预测偏差Fig.9 Difference of nitrogen content of refined gasolinewith using different prediction models

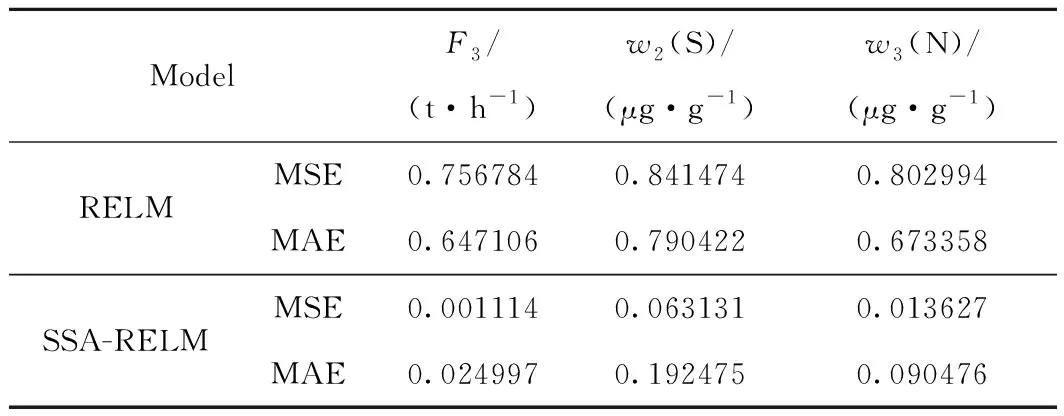
表2 预测误差计算结果Table 2 Calculation results of prediction error

3 多目标操作优化分析

S Zorb作为吸附脱硫装置，该装置的主要产品精制汽油的硫含量是最重要的指标，同时氮含量作为清洁燃料的指标之一也应适当予以考虑，此外在以上2个指标合格的情况下，精制汽油的流量越大可以保证获得越多的合格产品。如何平衡好3个指标之间的关系，以及如何对相应的操作变量进行调整，都是实际生产过程中需要考虑的关键问题。

笔者将精制汽油产品流量、氮含量和硫含量3个指标作为多目标操作优化分析的3个目标，以3#进料和加氢石脑油进料量的不同组合为例，分6个区((70000 kg/h,4000 kg/h)、(70000 kg/h,2000 kg/h)、(80000 kg/h,4000 kg/h)、(80000 kg/h,2000 kg/h)、(90000 kg/h,4000 kg/h)、(90000 kg/h,2000 kg/h))进行了多目标操作优化分析。按照以上分区方式，利用Aspen Plus仿真共得到18000组数据，每个操作区有3000组数据。

将每个分区的操作点对应的目标值在三维坐标系中画出。由于在多目标优化问题中，各单目标的优化方向相互冲突，对于硫含量和氮含量的预期目标应越低越好，而对于精制汽油产品流量应当尽可能大，同时不同的目标的量纲也不同。为了进行综合评价，将3个目标数据进行了归一化，并将精制汽油流量数据取为负值，使得多个目标变化趋势一致。然后，根据目标空间中各目标的分布情况，采用非支配排序的方法寻找Pareto前沿[21]，各区的3个目标分布情况如图10所示。

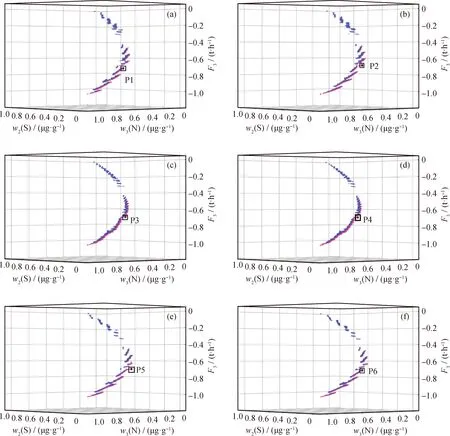
F3—Refined gasoline flow; w2(S)—Sulfur mass fraction of refined gasoline; w3(N)—Nitrogen mass fraction of refined gasoline图10 各分区的目标空间及Pareto前沿Fig.10 Objective space and Pareto front in each partition zone(a) Partition zone 1: (F1=70000 kg/h, F2=4000 kg/h); (b) Partition zone 2: (F1=70000 kg/h, F2=2000 kg/h);(c) Partition zone 3: (F1=80000 kg/h, F2=4000 kg/h); (d) Partition zone 4: (F1=80000 kg/h, F2=2000 kg/h);(e) Partition zone 5: (F1=90000 kg/h, F2=4000 kg/h); (f) Partition zone 6: (F1=90000 kg/h, F2=2000 kg/h)

图10(a)、(b)、(c)、(d)、(e)、(f)分别表示6个分区，对应的分区为：(70000 kg/h,4000 kg/h)、(70000 kg/h,2000 kg/h)、(80000 kg/h,4000 kg/h)、(80000 kg/h,2000 kg/h)、(90000 kg/h,4000 kg/h)、(90000 kg/h,2000 kg/h)。在每个子图中，蓝色点表示支配解，红色点表示非支配解，在非支配解中选择得到最优操作点。假设硫含量、氮含量和产品流量这3个产品指标权重相同，计算归一化后的操作点到点(0,0,-1)的欧氏距离，将该距离作为操作点综合评价指标，距离越小说明该操作点越好，其中距离最小的点作为该分区的最优操作点，即为图10中的P1到P6。各分区对应的3个目标重要程度相等时的最优操作点及其目标见表3。

从表3看到，操作点P5和P6的硫元素含量比限定值(不大于10 μg/g)高，因此在假设3个生产指标等权重的情况下，并不能得到合格的产品。在实际生产中需要向着硫含量低的方向调整，在Pareto前沿上优先选择使得硫含量更低的其他操作点作为实际操作点以保证产品的质量。

表3 图10中各分区最优操作点及目标Table 3 Optimal operation point and target for each partition in Fig.10

最后，笔者对表3中的5个操作变量对3个目标的影响程度进行了Pearson相关性分析，结果如图11所示。按照柱状图高度，可以依次排列5个操作变量的操作顺序。柱形图高度越高表明操作变量的优先级越高，在对S Zorb装置进行调整时，应当优先调整该变量。

T1—Heating furnace inlet temperature; T2—Hot separatortemperature; T4—Cold separator temperature;T5—Gas outlet temperature; p2—Hot separator pressure;F3—Refined gasoline flow;w2(S)—Sulfur mass fraction of refined gasoline;w3(N)—Nitrogen mass fraction of refined gasoline图11 操作变量的优先级计算Fig.11 Priority calculation of operation variables

在实际操作中，利用2.3节数据驱动模型对当前操作点进行实时预测，如果预测值与Pareto前沿中最优操作点有差距，则在本区内调整当前操作点向最优操作点移动，按照优先级依次调整干气出装置温度、热分压力和热分温度，其次对加热炉进口温度和冷分温度进行调整，按照该操作顺序可使得当前操作点迅速移动到最优操作点，提高实际操作的速率和效率，保证生产装置始终处于最优且稳定的状态。

4 结语与展望

分别建立S Zorb装置的机理模型和数据驱动模型，实现了对吸附脱硫装置在线产品预测和多目标的操作优化分析。

(1)根据实际的生产数据，利用GBDT模型计算24个操作变量相对于产品流量和硫含量的特征贡献度，再利用Aspen Plus软件建立S Zorb装置的机理模型，并通过有效性检验和灵敏度分析得到机理模型输入变量和输出变量。

(2)通过运行Aspen Plus机理模型扩展数据集。利用麻雀搜索算法对正则化极限学习机进行改进，以原料进料流量和硫含量、加热炉进口温度、加氢石脑油进料流量、热分压力、热分温度、干气出装置温度、冷分温度为输入，精制汽油的流量、硫含量和氮含量和干气流量为输出建立了SSA-RELM模型，在保证训练速率的情况下进一步提高了预测精度，实现了产品指标在线预测。

(3)最后通过对进料分区，分析了不同进料情况下操作点的分布情况，找到了6个分区上Pareto最优解和最优操作点，给出了实际操作过程中操作变量调整的优先级，从而实现精制汽油产品流量、硫含量和氮含量3个优化目标的在线操作指导。

(4)基于炼油厂实际的工艺手册和有限的现场数据建立了S Zorb装置模型。在后续的研究中，将进一步探究在引入干扰变量和复杂进料条件下的模型运行状态，提升模型的抗干扰能力。