基于雷达方程修正的目标探测距离评估方法

董云龙 刘洋 刘宁波 丁昊 关键

（海军航空大学，山东烟台 264001）

1 引言

第二次世界大战中，为了评估早期雷达系统的性能，雷达距离方程被逐渐发展起来，用于在特定的雷达、目标和环境参数中计算出雷达的最大探测距离。经过70多年的发展，方程的形式和内容跟随现代雷达的技术不断革新而逐步丰富。

早期的雷达方程主要是计算雷达在噪声背景下对空目标的最大探测距离，比较典型的就是Blake 脉冲雷达方程［1-2］，包括后期在干扰条件下的应用［3］。而后为适应不同的探测环境，雷达方程进行了不同的调整，使其在面杂波和体杂波背景下也能适用。虽然方程在不断的完善，但是方程中的参数依然是计算的主要问题。例如，简单目标的雷达横截面积（Radar Cross Section，RCS）可以用公式计算且基本保持恒定，但是位于海面上以后，其与海杂波的相互作用会产生复杂的散射特性，进而在计算的过程中会有起伏［4］。同时，环境参数和雷达系统的参数要远比方程的固定取值复杂，且很多参数都与距离存在函数关系［2］，一般情况下难以通过简单计算得到。对海雷达也要充分考虑到目标所处的环境，主要是考虑海杂波对目标探测的影响程度。因此，在参数和探测环境不明确的情况下，计算海上目标的最大探测距离就会出现较大的误差。

目前，针对海杂波背景下雷达距离方程的研究很少。文献［2］给出了某些体制的雷达在面杂波背景下的距离方程，这些方程中杂波的平均功率定为固定值，且幅度分布服从于高斯分布，即杂波与雷达的噪声具有相同的性质，杂波的存在仅仅是提高了目标检测背景的“噪声功率”。但这些方程并不适用于对海探测，因为海杂波并不是固定值，其不仅与距离有关，也与入射余角的大小有关，且高分辨率下的海杂波更加符合非高斯分布。海面上某些简单目标的RCS 较独立状态下的RCS 更加复杂，其与距离和入射余角也存在着函数关系。一般的雷达方程并不适用于高分辨率对海雷达的最大探测距离的计算。

鉴于现有的雷达方程以及参数值不足以用来评估对海雷达的最大探测距离，本文提出了利用已知的参数和实测数据来修正方程以达到较为准确评估雷达性能的方法。简化和修正的信杂比方程计算得到的结果，与该型号对海雷达在试验中显示的结果基本相同。

2 雷达方程

2.1 基本雷达方程

雷达的距离方程于二战期间发展起来，被用于分析那个时期的雷达探测性能。从最初的简单的雷达方程开始，研究者将各种影响探测距离计算的因素逐步量化到雷达方程中，使得雷达方程计算复杂情况下的探测距离更加精确。文献［2］给出了雷达系统的一般方程：

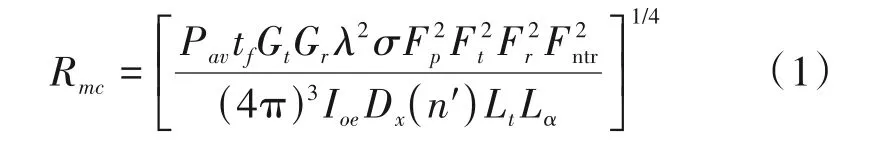
式中，Pav是脉冲的平均功率（W），tf为相参处理时间（s），Gt为发射天线增益，Gr为接收天线增益，λ为波长（m），σ为目标的雷达横截面积（m2），Fp为收发天线的极化失配，Ft为发射路径的方向图传播因子，Fr为接受路径的方向图传播因子，Fntr是随距离变化的雷达响应因子的乘积，Fntr=FeclFstcFbdFfdFlens2，Fecl是遮蔽因子，Fstc是STC 因子，Fbd是波束驻留因子，Ffd是频率分集因子，Flens2是双向透镜因子。Ioe是杂波Coe加噪声No的能量（J），Dx(n′)是有效检测因子，Lt是发射馈线损耗，Lα是双向路径的大气吸收损耗。

上述方程可以定量的求解Rmc的值，即雷达的最大探测距离。一般可以依据方程利用图形法或者求根算法得到，两种算法的本质都是将信号能量E和IoeDx(n′)分别表示成距离的函数，然后求出两个表达式相等的最大R值［2］。

2.2 方程应用的局限性

雷达方程是基于基本的雷达信号传输过程建立的，方程中的参数涉及雷达系统、环境和目标等多个环节，参数众多且互相之间还有作用关系，进而导致在实际应用中，方程会有诸多局限性。

（1）方程中的噪声不仅包括雷达的天线噪声和接收机噪声，还有系统内部元器件的噪声，如A/D转换器。要确定方程中的噪声，就要得到目标检测前雷达系统各个元器件的噪声值。但是噪声值并不是恒定的，在长期的使用中发现，噪声值会因为探测环境的不同出现小范围的波动。实际操作中，噪声的获取有两种方法，一种是获取雷达厂家对雷达噪声的测量结果，另外一种则是借助中频回波数据通过帕萨瓦尔公式计算得到。厂家的详细性能指标一般不容易获得，因此本文通过计算得到。

在频域中，白噪声能量分布在整个频带内且服从于均匀分布，而海杂波能量则集中分布在相应的多普勒频带内。利用对海雷达的中频回波数据，取一无目标的雷达分辨单元做频谱分析，如图1所示。

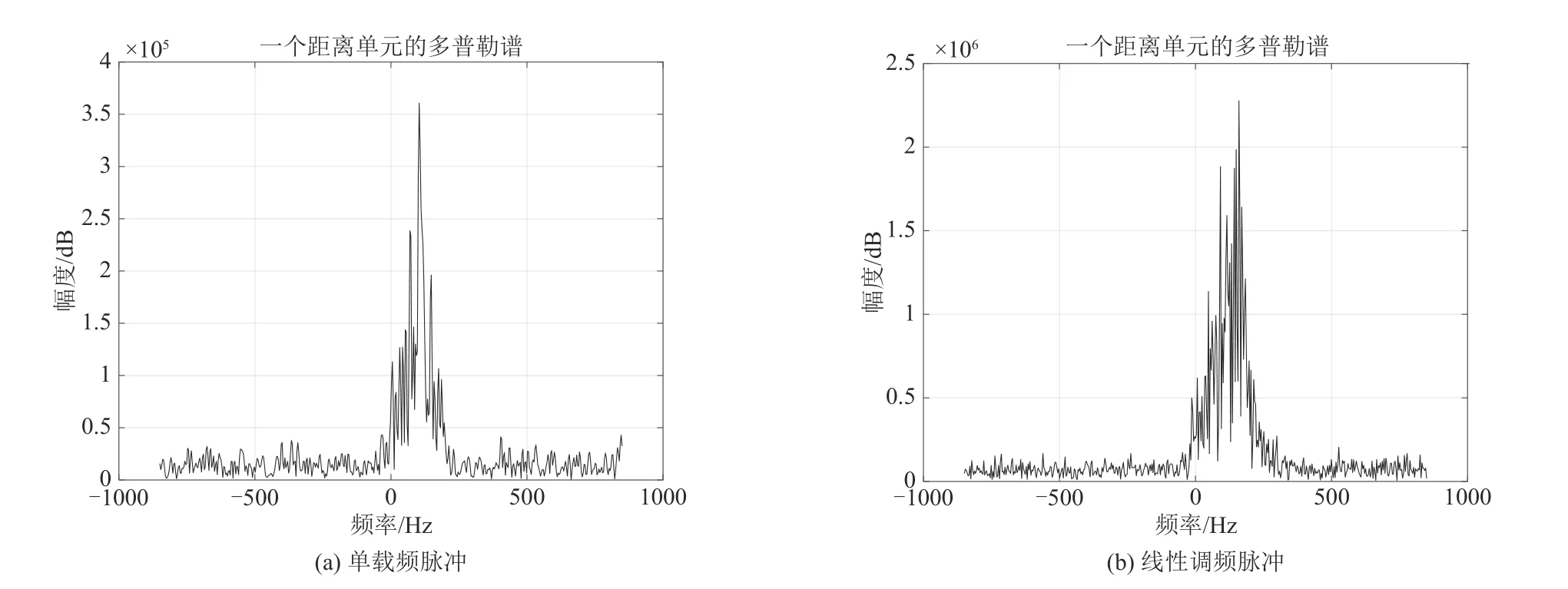
图1 多普勒频谱Fig.1 Doppler spectrum

图1 为两个脉冲在同一距离单元的多普勒频谱，中间幅值较大频带内为海杂波与噪声的能量和，两边幅值较低的频带内几乎都是为噪声能量。分别在两边幅值较低的频带各取几百个频率点的幅值，取均值后作为频谱中每个频率点的噪声值。再根据Plancherel定理

求得此次试验中雷达在单载频脉冲和线性调频脉冲的噪声能量分别约为60 dB和69 dB。

（2）单脉冲检测时，有效检测因子Dx(n′)与探测概率、虚警概率、检测背景与目标的幅度分布和目标检测的方法有关。在确定检测因子Dx(n′)时，要确定对海雷达在进行目标检测时的背景环境和检测方法，尤其是对海雷达进行恒虚警检测时，要考虑海杂波幅度分布对虚警门限的影响。

如果雷达将海杂波纳入检测背景进行恒虚警检测，那么就要考虑海杂波的幅度分布情况。对于低分辨率的雷达，海杂波被认为是服从于高斯分布或瑞利分布，与噪声的幅度分布相同，而高分辨率对海雷达的海杂波幅度分布则服从于非高斯分布［5］。对于无目标的海上距离单元，其雷达回波信号的能量为海杂波和噪声的能量之和，幅度分布也与海杂波与噪声的能量之比的大小有关。

利用该型号试验雷达在烟台某海域获取的3-4 级海况下的中频回波数据［6-7］，拟合几种常见的海杂波幅度分布模型，其中包括高斯分布、瑞利分布、对数正态分布、韦布尔分布和K 分布等。针对不同的波形分别选择两个不同的距离单元，取每个距离单元的10000 个脉冲的回波，画出如图2 所示的信号回波图。将10000个脉冲的幅度值对其中最大的幅度值进行归一化，并将0-1 区间内评分为若干个小区间，分别将归一化后的幅度值做累积分布函数CDF（Cumulative Distribution Function，CDF），根据CDF 计算出经验概率密度函数PDF（Probability Density Function，PDF）。各幅度分布的拟合则是根据归一化的10000个脉冲数据分别计算出各个幅度分布的参数，如高斯分布的均值和方差，K分布的形状参数和尺度参数，依参数画出各个幅度分布模型。绝对误差则是取各个幅度分布与经验PDF 的差值的平均值。拟合结果如图3、图4所示。

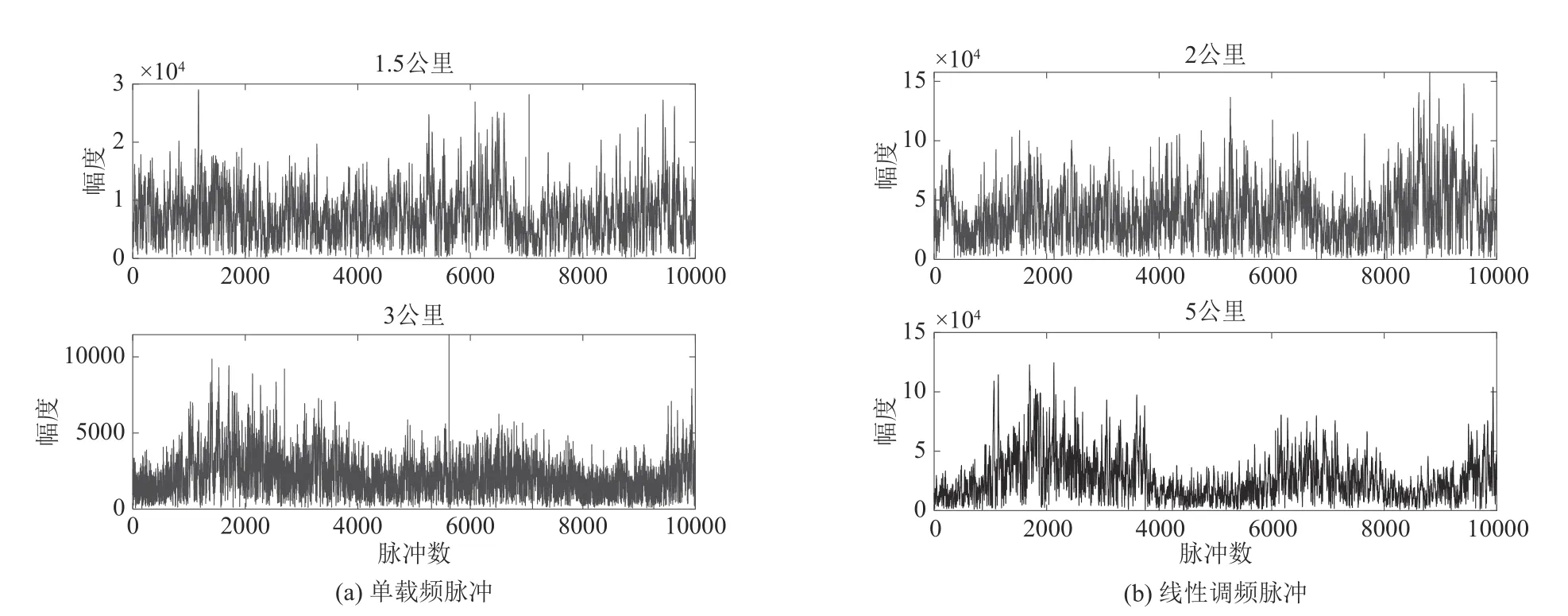
图2 不同距离单元的信号回波图Fig.2 Signal echo map of different range cells

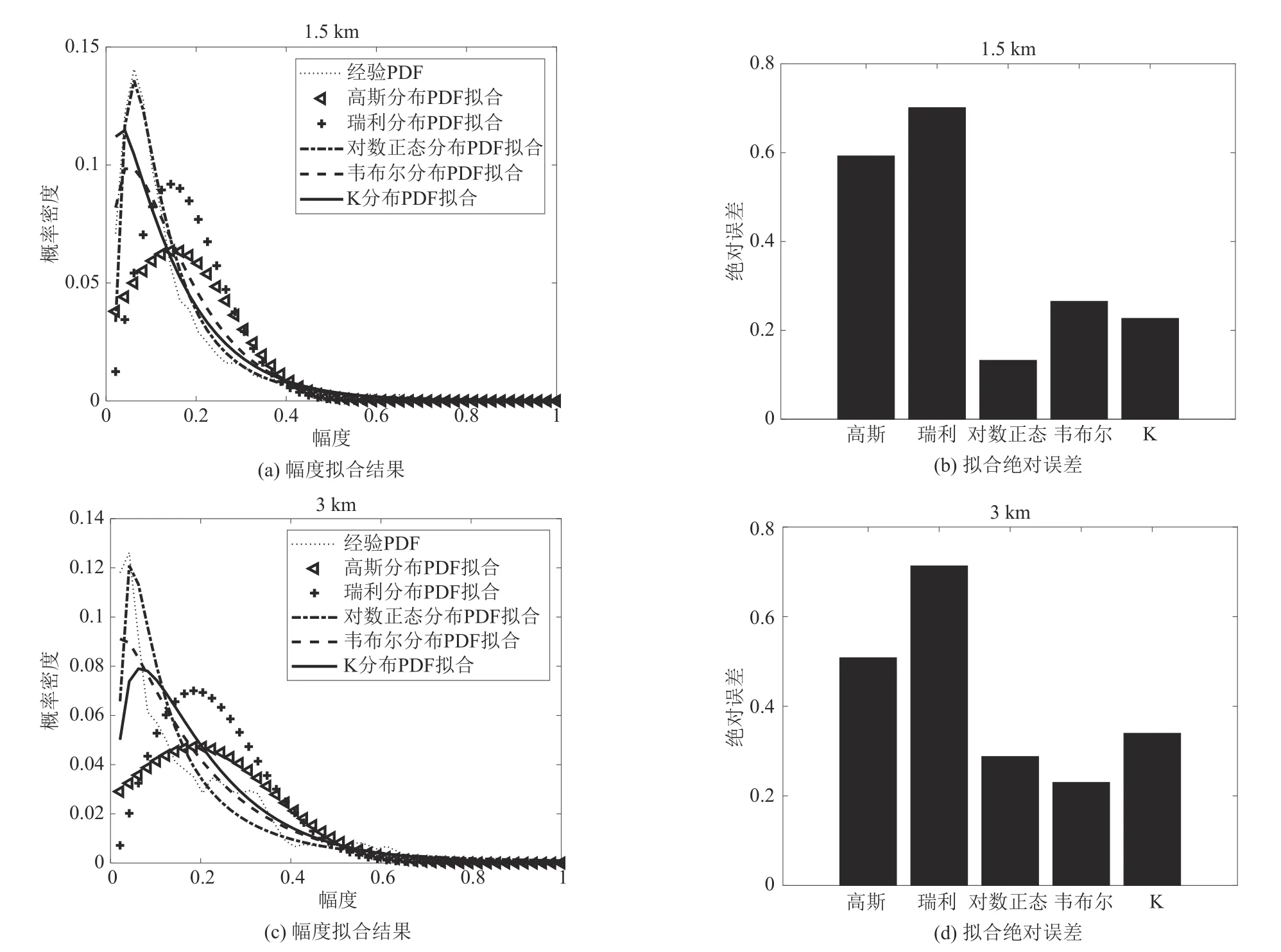
图3 单载频脉冲幅度拟合结果和拟合绝对误差Fig.3 Results of single carrier frequency pulse amplitude fitting and absolute error of fitting

观察图4中的图（a）和图（b），在近距离处，海杂波的能量高于噪声能量，雷达回波信号的幅度分布特征为海杂波的幅度分布特征，其幅度分布服从于非高斯分布。图（b）中，距离的增加使得海杂波与噪声的能量比逐渐减小，雷达回波信号幅度分布受到噪声的影响而逐渐趋近于高斯分布。

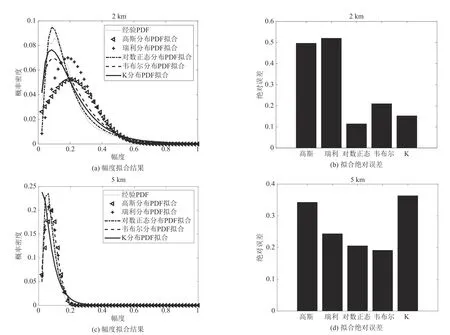
图4 线性调频脉冲幅度拟合结果和拟合绝对误差Fig.4 Results of LFM amplitude fitting and absolute error of fitting

如果对海雷达在探测的过程中，海杂波作为检测背景进行目标的恒虚警检测，必然要以非高斯分布来确定Dx(n′)才能保证要求的恒虚警。而且不同距离上的雷达回波幅度分布也会发生变化，相比于噪声背景下的Dx(n′)，海杂波背景下的Dx(n′)不仅要估计检测背景的平均功率，还要根据不同的幅度分布确定不同的计算公式［1］。

（3）方程的计算建立在确定雷达的最小可检测信号的基础上，而实际上由于脉冲多普勒处理等数字信号处理技术的广泛引用，接收机输出的信号处理允许检测远低于接收机噪声的信号。并且随着海面小目标检测技术的发展［8］，方程的计算结果也许将不能反映雷达实际探测的结果。

（4）试验雷达在探测过程中，即使是试验球这样的小目标也会经历几十个脉冲，而方程是建立在单脉冲或者是脉冲积累的情况下。多脉冲探测的存在会影响检测门限值，进而影响雷达实际最大探测距离的计算［9］。

（5）试验中导体球为规则球体，其RCS 大约为其投影面积。但是，当导体球位于海面上时，其RCS就会出现起伏特性［4］。这种起伏特性就会导致目标的回波功率同距离的函数关系发生变化，进而在计算的过程中产生误差。

3 试验条件和过程

试验雷达采用X 波段民用雷达，试验中部分已知的试验参数见表1。

表1 雷达参数Tab.1 Radar parameters

本次试验中的雷达发射脉冲为两种波形，一种是单载频的简单脉冲T1，脉冲宽度为0.04 us；一种是线性调频脉冲（Linear Frequency Modulation，LFM）脉冲T2，脉冲宽度为3 us。

本次试验是在烟台养马岛海岸上进行，雷达架设在高度为33 m 的岸边对海探测，海况约为二级偏低海况。试验中目标为形状规则的导体球，直径约为0.6 m，其独立RCS 约为0.25 m2。导体球被船舶牵引做远离雷达的匀速直线运动。图5 和图6 为试验场景图和雷达显示图，图6 中圆圈标记中的前侧为船舶大目标，后侧为小球目标。雷达显示目标探测的最大距离约为4.6 公里。试验中，采集雷达每一圈扫描的中频回波数据，具体试验过程和部分数据已经发表在文献［6］中。

图5 试验设备Fig.5 Test facility

图6 雷达显示图Fig.6 Radar display

4 计算探测概率和探测距离

2.1 节提供了计算最大探测距离的方法，即取信号能量E与IoeDx(n′)相等时所对应的距离，而Dx(n′)的值是根据探测概率、虚警概率和干扰能量Ioe来确定。理论上是很难知道雷达究竟是以何种干扰背景分布、虚警概率和探测概率来确定Dx(n′)。换句话说，即使是同样的Dx(n′)，不同的干扰背景分布和虚警概率下探测概率是不同的。这里最典型的就是噪声背景下的单元平均恒虚警检测，要比已知噪声功率的固定门限检测，在相同的探测概率下Dx(n′)要大，即存在检测损失。而且不同干扰背景分布下的虚警概率、探测概率和信噪比的对应关系是不同的［5］。本文采用表1 提供的虚警概率、探测概率和信噪比，不考虑其取值依据。

首先计算雷达扫描一圈时，扫描到目标的脉冲数。试验中雷达为转速为2 转/分钟，扫描一圈为30 秒，脉冲重频为3 kHz，则雷达扫描一圈的脉冲数为90000 个。雷达的波束宽度为1.2°，则雷达主波束扫描一圈扫到目标的脉冲数为(1.2 × 3000 ×30)/360=300个。

在天线扫描目标的过程中，目标相继被天线波束的边缘和波束中心扫描到。波束宽度内的天线增益最大能相差3 dB，在波束驻留时间内的脉冲，其波束中心扫到目标的增益要大于波束边缘扫到目标的增益。为了尽量减小天线增益对回波功率的影响，选择波束驻留时间内的波束中心前后100 个脉冲，即为天线波束中心对准目标时前后的100 个脉冲。同时，为了避免在扫描过程中目标起伏过大带来的影响，本文选择连续三次扫描的共300 个脉冲。也就是说，选取的300 个脉冲分别是相邻的三次扫描结果中的最接近波束宽度中心的100个脉冲。

其次，对中频回波数据采取过“门限检测”。该“检测门限”不是虚警门限，而是雷达回波的“门限”，重在找到该信噪比下的探测概率。根据表1厂家提供的两个信噪比值，进而可以确定两个脉冲在不同探测概率和虚警概率条件下的“检测门限”。

经过检测得到的探测概率-距离的曲线图如图7所示。

根据图7 可以得到在信噪比分别为13 dB 和11 dB 时，不同的探测概率对应的探测距离。在信噪比为13 dB、探测概率为0.9 时，LFM 脉冲对应的距离约为3 公里，这是根据雷达距离方程计算的单脉冲检测的结果。实际上，根据图6 可以看出目标在雷达显示的距离约为4.5 公里，而且显示的比较稳定。前面分析到，雷达的多脉冲检测和信号处理等会影响雷达的最大探测距离，而且在目标即将消失的距离段中，目标能量与海杂波能量之比很小。超过了13 dB或11 dB的雷达回波信号，可能是海杂波的能量而不是目标的能量。

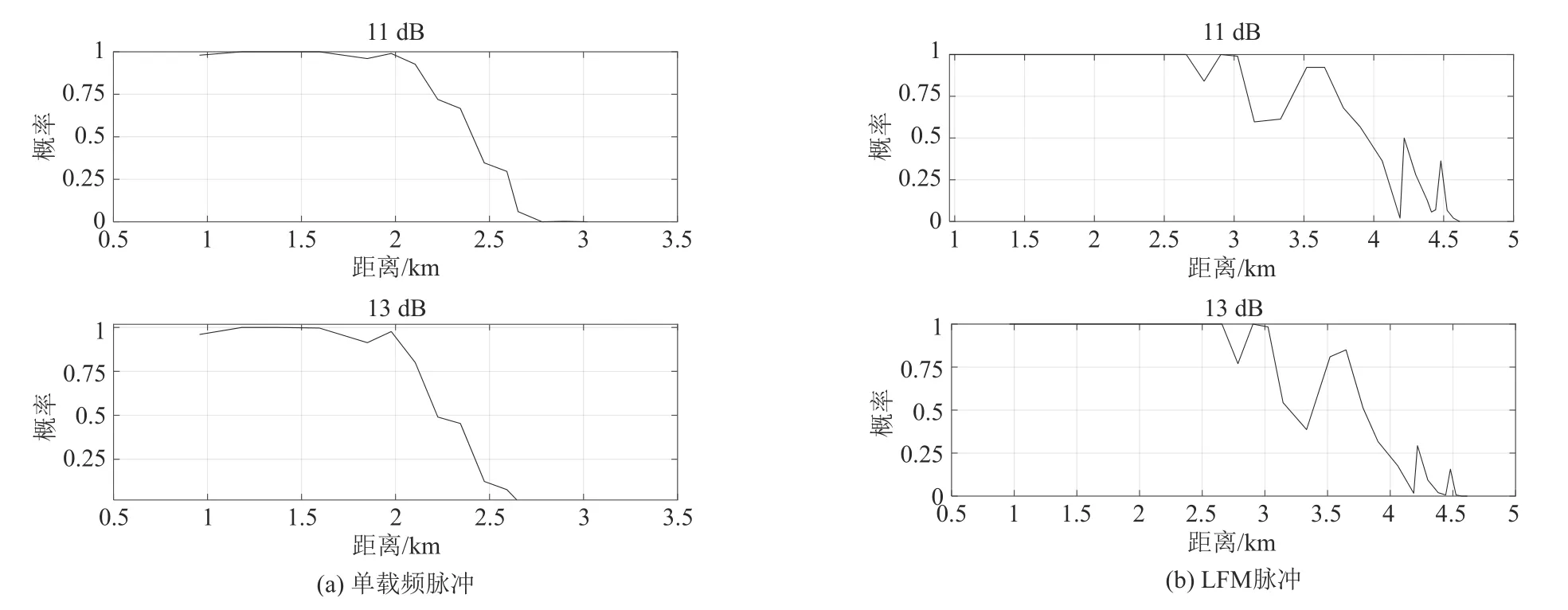
图7 不同信噪比的探测概率-距离曲线Fig.7 Detection probability-distance curves of different SNR

针对目标消失的原因，这里主要考虑海杂波对目标探测的影响。试验中的雷达没有对海杂波进行抑制处理，如果信杂比接近于0 dB，而信噪比和杂噪比较高，就会导致在检测的过程中出现多个“目标”，而理论上只有一个目标，其他“目标”都是因海杂波引起的“虚警”。为了保证目标能够被雷达完全探测到，也为了后期跟踪处理，目标的回波功率不仅要满足噪声背景下的信噪比，还要保证较高的信杂比。

5 杂波背景下的雷达方程

前面分析道，假如目标和海杂波都能够被完全检测到，当目标能量低于杂波能量时，目标就会被大量的海杂波“虚警”淹没。因此，目标不仅要能够根据雷达方程被检测到，还要高于海杂波能量。

5.1 信杂比方程

在低掠射角下，假设杂波与目标在同一距离单元内且是完全相关的，那么杂波和目标的回波能量所受到的损耗和增益基本相同，所不同的是目标的横截面积σt和杂波的横截面积σ0Ac，即二者的能量之比S/C就是横截面积的比值。

其中，海面照射面积Ac与雷达的天线波束形状和观察的几何结构有关［1］。该型号雷达在脉冲限制下的海面照射面积的计算公式为：

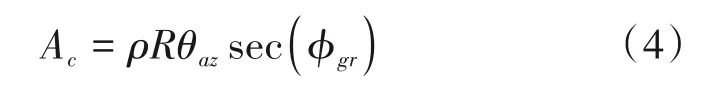
由式（3）和式（4）得在以海杂波为主要干扰下的雷达探测距离方程可以表示为：

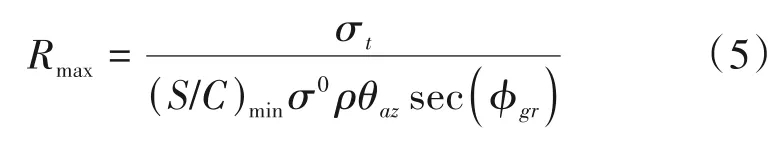
从该公式入手，计算雷达的探测距离就以归纳为对海杂波反射率和相关参量的计算。ρ是雷达的距离分辨率，θaz是天线方位波束宽度，ϕgr是本地的入射余角，文献［1］给出了其计算公式：

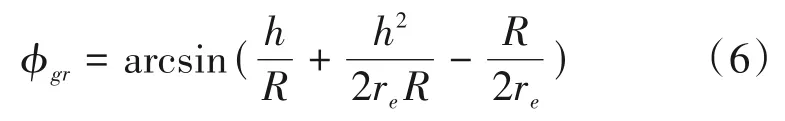
式中，h是雷达的高度（海拔），re是地球半径，R是雷达到目标的距离。

5.1.1 后向散射系数模型

海面回波是位于雷达分辨单元的各散射元所产生的。1950年，每单位表面积的雷达截面积σ0的概念被引入，以作为一种能用来描述雷达截面积的归一化参数。理论研究表明，σ0受多种因素的影响，如雷达参数中的频率、极化方式、分辨单元的大小和入射余角等以及海洋环境参数中的风速风向、浪高浪向和大气波导等。多年来，国内外的研究者们利用采集到有价值的后向散射系数数据，结合海面散射和传播机理，拟合出了σ0与不同影响参数的对应关系，并归纳出许多描述σ0的数学模型［10］。这些模型能够定量的描述海面杂波的回波强度，在计算雷达探测距离时发挥着重要作用。在低入射余角下，σ0模型主要有GIT、HYB、TSC、NRL和SIT等模型［11-12］。

试验中，运动小球的擦地角如图8所示，在雷达探测的重点区域上，目标的擦地角都在10°以下。根据雷达显示的结果，目标最大的探测距离在4 公里至5公里之间，在此擦地角下，采用低入射角下的σ0模型足以评估雷达的最大探测距离。

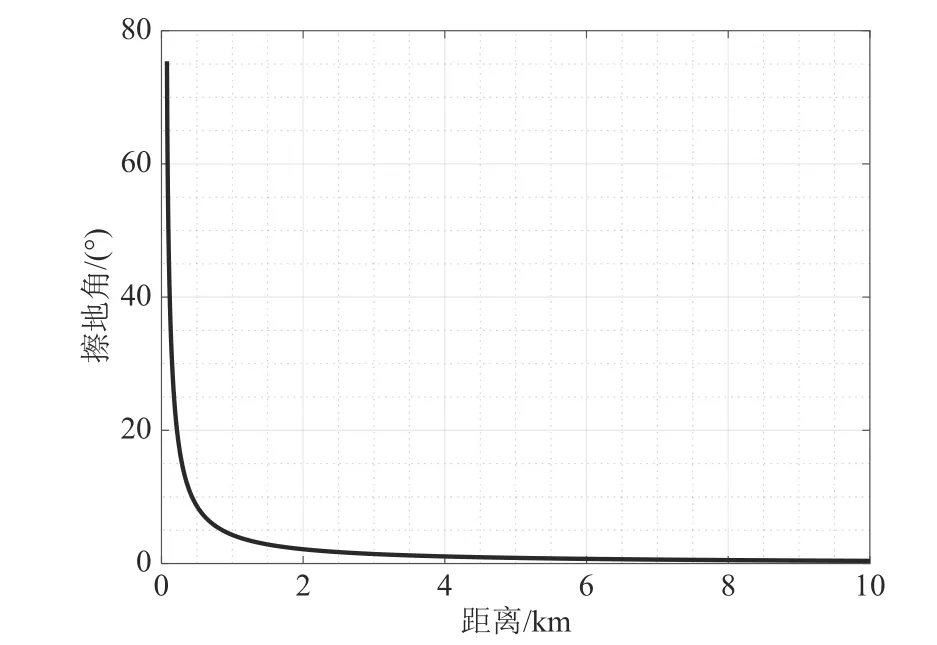
图8 擦地角Fig.8 Grazing angles

将各个低入射余角模型对实际σ0的拟合情况进行对比［13-14］，可以看出改进NRL 模型对低入射余角和低海况的拟合程度是最好的，TSC 模型次之，GIT 和HYB 模型拟合较差。虽然改进NRL 模型拟合度最好，但是其只有在侧风情况即雷达观察角与风向成90°下才适用，而本次实验是顺风，因而本次试验采用TSC 模型和GIT 进行仿真，两者在低入射余角下的误差并不是很大。

图9 中可以看到，在1 公里到6 公里的区间内，TSC 模型随距离的变化缓慢，几乎是个定值，而GIT模型变化快，在后半段大概与距离R-4是成正比。在小擦地角的对海探测中，海杂波随入射余角的变化中存在一个“临界角”，这个“临界角”居于几度的范围内。在这个角度以下，σ0随着角度的减小而迅速减小，使得海杂波的回波功率可能会与距离R-7成正比。而在这个角度以上，σ0上升得更慢，或者基本保持不变，杂波功率基本上与距离R-3成正比。结合图9中的σ0模型，GIT模型相比于TSC模型更能体现出这种小擦地角带来的回波功率迅速衰减的情况。

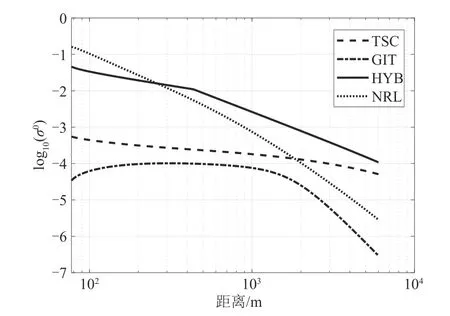
图9 不同模型下σ0的对数值Fig.9 The logarithm value of σ0 under different models

5.1.2 仿真计算

虽然海面上目标RCS计算十分复杂，但此次模型构建中将目标的RCS值作为一个固定值进行计算，其与距离的函数关系将融入到后期增加的参数中。下面是根据公式（3）仿真得到的信杂比随距离的变化图。

图10 中可以看出，利用公式（3）计算得到的信杂比在1 km 后并未随着距离衰减，反而有上升的趋势，其中GIT 模型更加明显，这说明公式（3）并不适用于计算对海雷达的信杂比，也无法计算出信杂比为0 dB时对应的距离。

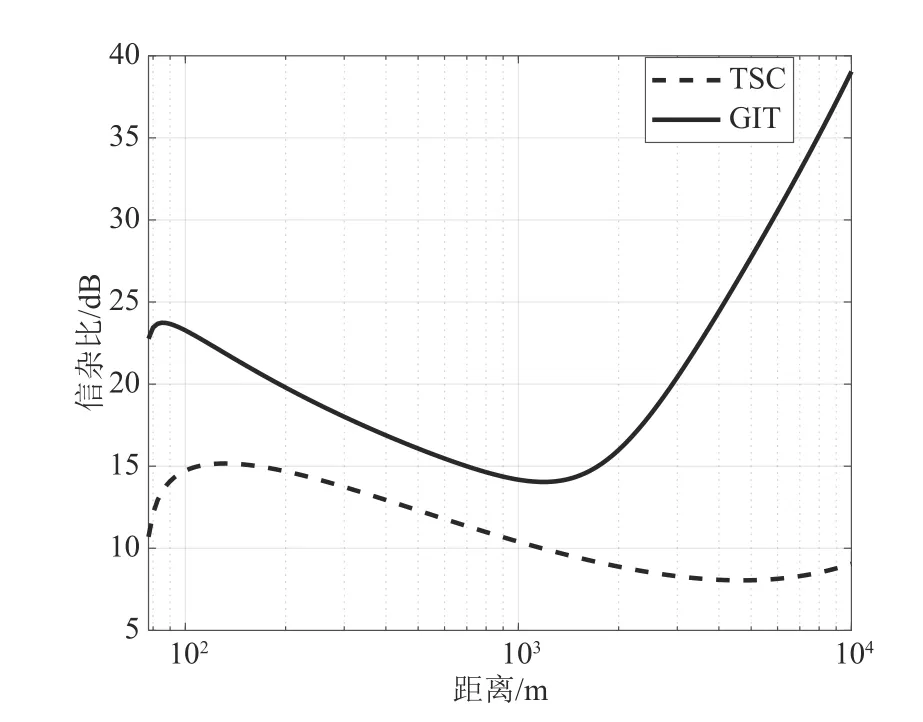
图10 信杂比随距离的变化曲线Fig.10 The change curve of signal-to-clutter ratio with distance

5.1.3 修正内容

（1）起始信杂比

在中高入射余角下，试验数据得到的信杂比要高于公式计算的信杂比。单载频脉冲的信杂比平均高6 dB，LFM脉冲的信杂比平均高20 dB。

（2）信杂比的变化规律

根据中频回波数据计算不同距离下的信杂比，并寻找信杂比的变化规律。试验中的雷达在同一条件下能够发射两种脉冲体制，表2和表3分别为单脉冲下回波信号的信杂比值和LFM脉冲下回波信号的信杂比值，图11为实测数据与仿真模型的比较图。

表2 单载频脉冲下回波的部分信杂比值Tab.2 Partial signal to clutter ratio of single carrier frequency pulse

表3 LFM脉冲下回波的部分信杂比值Tab.3 Partial signal to clutter ratio of LFM pulse

5.2 距离方程进行修正

5.2.1 修正过程

由于中高入射余角的海杂波幅度分布较为分散，因此对于方程在中高入射余角下的情况本文不予以考虑，而是将修正的重点放在一公里以后，即低入射角下的距离方程。基于实测数据对方程进行修正主要分为两个步骤，一是将一公里前的仿真数值提高到跟实测数值大致相等；二是将实测数据和仿真数据的误差修正到距离方程中。以图11（b）中的数据为例推导方程的修正过程：

（1）根据图11（b）中的实测信杂比数据的一维线性回归模型计算得到1 km处的信杂比约为40 dB，然后将公式（3）加上40 dB，这等同于将图11（b）中的TSC 仿真模型向上平移40 dB。这样修正后的公式在1 km 处计算得到的信杂比接近于实测数据，同时也提高了各个距离点计算值。

（2）在1 km 后取若干个距离点，分别计算图11（b）中一维线性回归模型和第一步得到的新公式在所取距离点上的信杂比值，用后者减去前者并进行一维线性拟合。

图11 仿真与实测数据Fig.11 Simulation and measured data

（3）将第一步修正后的公式与第二步拟合的结果进行相减，就得到了新的距离方程。需要注意的是，相减只是在1 km以后的距离段进行。1 km之前的距离段内由于缺少实测信杂比数据，因此仍然保留第一步得到的结果。

5.2.2 修正结果

根据上述的修正过程，分别对两种脉冲在不同σ0模型下的公式进行修正。修正的过程中，TSC 模型在1 km 以后的距离段进行修正，GIT 模型则是在2 km以后的距离段进行修正。

两种脉冲在TSC模型下进行修正得到的结果：

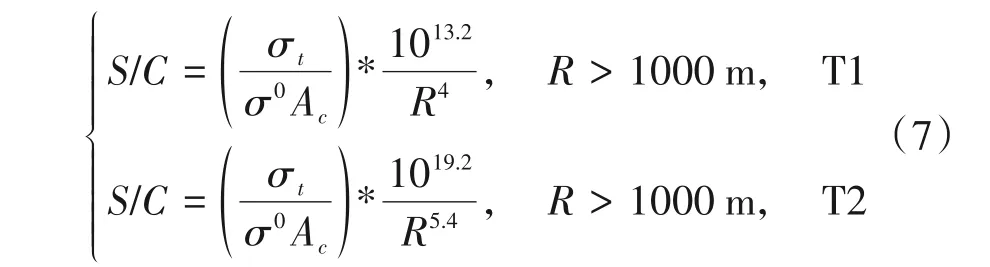
图9 中可以发现，TSC 模型的σ0大约与距离R-1成正比，那么可以认为杂波横截面积σ0Ac变化很小，几乎与目标横截面积σt一样是一个定值，则修正后的方程大约就是实测数据与距离R的关系。

两种脉冲在GIT模型下进行修正得到的结果：

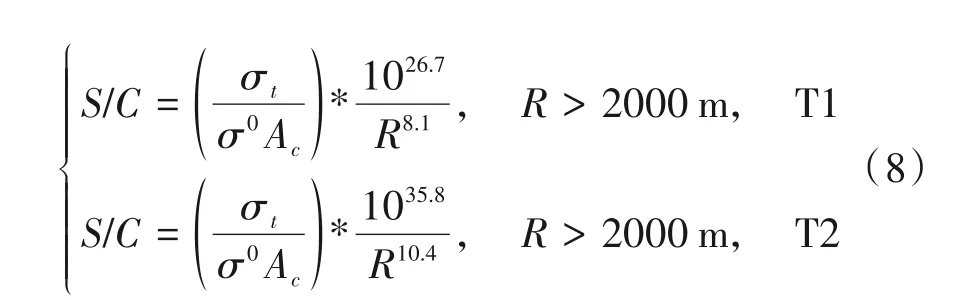
图9 中，GIT 模型的σ0大约与距离R-4成正比，那么σ0Ac大约与距离R-3成正比。式（8）中，根据实测数据修正的雷达方程分别与距离R8.1和R10.4成正比。其中，GIT 模型之所以从两公里处进行修正，是因为GIT 模型在1～2 公里之间有一个极点，影响结果，故选择在两公里处进行修正。

5.3 计算最大探测距离

此方程适用于以噪声为背景进行目标探测的对海探测雷达，在信噪比和杂噪比较高而信杂比较低的情况。图14 为未方程修正后的信杂比随距离的变化曲线和修正方程的信杂比随距离的变化曲线。

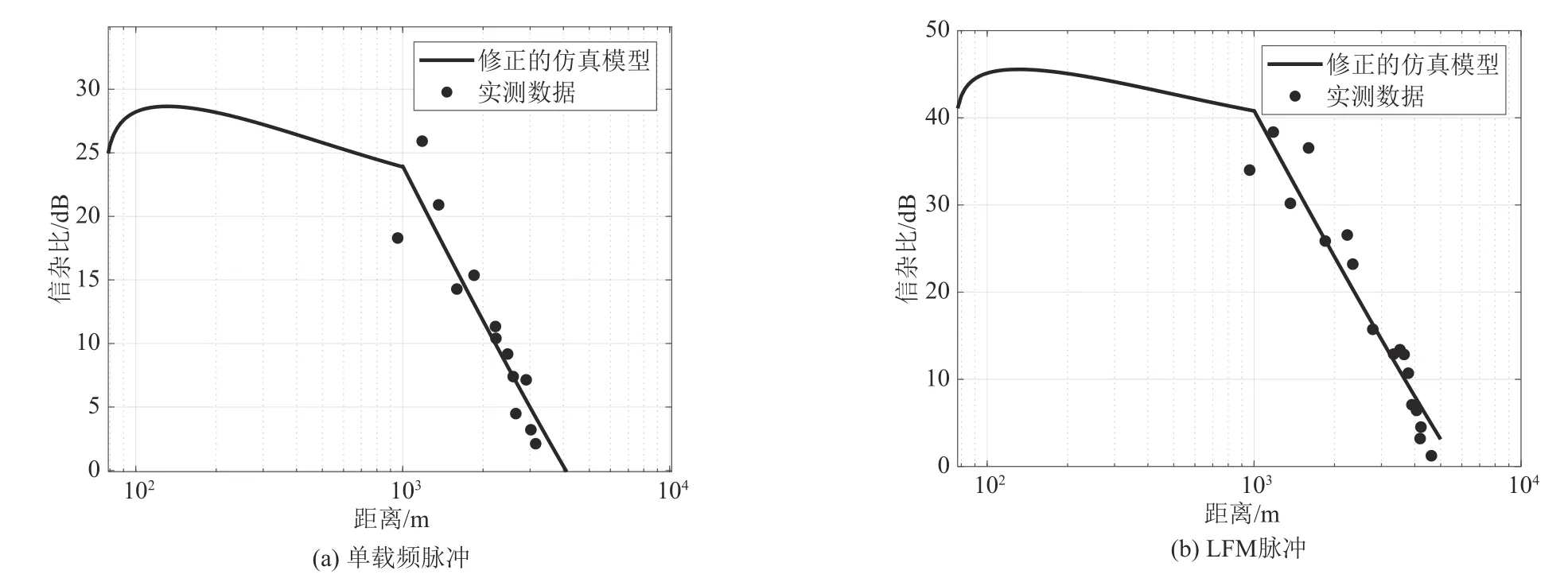
图12 TSC模型下方程的修正结果Fig.12 The modified result of the equation under TSC model

图13 GIT模型下方程的修正结果Fig.13 The modified result of the equation under GIT model

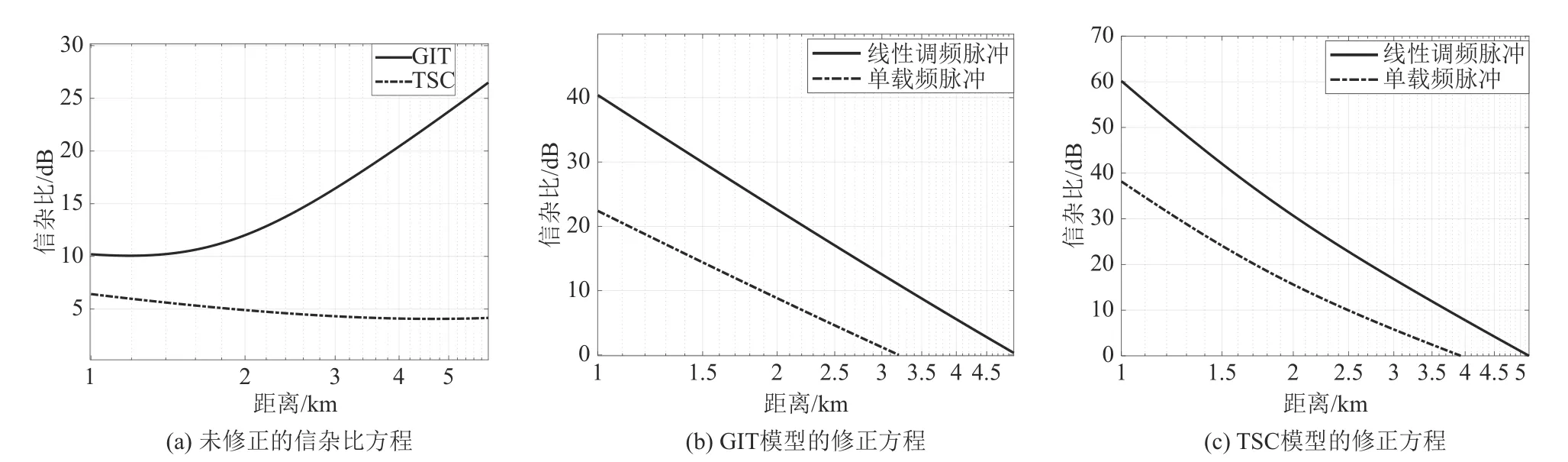
图14 信杂比随距离的变化曲线Fig.14 The change curve of signal-to-clutter ratio with distance

信杂比为0 dB 时，可以分别计算修正后的方程所得到的最大探测距离。

表4 修正方程得到的最大探测距离Tab.4 The maximum detection range obtained by modified equation

图14可以看出，未修正的信杂比方程是无法得到0 dB 时对应的距离，而修正后的信杂比方程得到的最大探测距离接近于雷达显示结果，证明了其实际应用中可能性。实际上在信杂比为2 dB 时，目标和海杂波就很难辨别。因此在利用修正后的方程时，可以根据雷达实际情况取信杂比的最小值。

6 结论

本文在一般雷达方程的基础上，利用雷达探测海上运动目标的中频回波数据，对方程进行了简化和修正。在简化的过程中，考虑到对海探测中海杂波的影响，将一般雷达方程简化为信杂比方程。修正的过程中，根据实际信杂比随距离的变化关系，对信杂比方程进行了修正。利用修正后的方程计算得到的对海雷达对该类型目标的最大探测距离与雷达显示结果基本相同。