地铁盾构隧道内径扩增对结构抗变形能力影响研究

黎 庆,赵旭伟,张小会,姜海波

(1.南京地铁建设有限责任公司,南京 210017； 2.中铁上海设计院集团有限公司,上海 200070；3.上海市轨道交通结构耐久与系统安全重点实验室,上海 201804)

引言

近年来，随着城市轨道交通结构设计理念的转变，以及轨道交通工程施工技术水平的持续提高，隧道内径增大成为盾构隧道工程的发展趋势[1-2]。大内径盾构隧道的明显优势在于其较大的设计断面界限空间，不仅满足了通行列车的大型化，提升了运量，还提供了充足的配套设施安装空间，且为后续结构变形整治提供了足够的操作空间[3]。

隧道管片的变形、内力分布与其本身的结构尺寸直接相关，不合适的尺寸改动可能导致管片产生过大变形或承受过大内力[4]。此外，扩径后的管片变形特性受外部环境影响更为显著[1]。若面临意外超载[5]、邻近开挖[6]、不均匀沉降[7]等特殊工况，扩径隧道管片可能发生因强度、刚度及稳定性不足所导致的“致命性”破坏，还可能出现结构渗漏、破损和大变形等耐久性问题[8]。因此，隧道内径扩增及扩径后隧道结构抗变形能力仍是需探讨的课题。

目前，对盾构管片结构受力、变形的研究可采用数值模拟[9]、理论计算[10-11]和试验等方法。国内外学者对隧道结构进行试验研究的主要手段可分为现场试验[12-14]，足尺试验[15-16]和模型试验。相比于足尺试验，相似模型试验在时间和材料成本上较为经济，且能较真实地反映试验结果。何川等[17]采用相似模型试验，研究了高水压条件下的超大断面隧道管片受力行为，讨论了衬砌拼装方式对管片内力的影响；FANG等[18-19]开展了几何相似比1:10的模型加载试验，研究了水压、土压及土体侧压力系数对管片受力的影响，并用有限元软件对试验结果进行了验证；梁东等[20]针对软土地区地铁沿线工程活动导致盾构隧道收敛变形增大的问题，采用相似模型试验研究了侧向压力变化对隧道结构变形、受力的影响规律。上述部分试验模拟了实际工程中的超载或侧方卸载工况，而就隧道结构变形的本质而言，荷载比(水平荷载和竖向荷载比值)变化是隧道变形的关键控制因素[20]。

目前，上海、南京等城市常见隧道为内径5.5 m，厚度0.35 m。基于5.8 m内径盾构隧道管片在南京地区的首次应用，考虑上覆超载工况开展几何相似比为1∶10的模型试验，研究了隧道管片内径扩增对结构内力和抗变形能力的影响，同时探讨了扩径后隧道管片的厚度优化，研究成果可供隧道结构设计参考。

1 模型试验方案

1.1 隧道结构原型

以南京地铁9号线盾构隧道管片为原型，全环由1个封顶块(1×21.5°)、2个邻接块(2×68°)、3个标准块组成(3×67.5°)，管片混凝土等级C50，环宽1.2 m，相邻环180°转角错缝拼接。南京市以往地铁隧道大多为内径5.5 m，厚度0.35 m，而9号线将内径扩大为5.8 m。因此，试验选择内径分别为5.5 m和5.8 m，厚度均为0.35 m的管片作为原型管片，进行相似模型试验设计。此外，基于管片内径增大可能导致其受力、变形处于不利状态的考虑，针对5.8 m内径的管片，增设厚度分别为0.3 m和0.4 m作为原型进行模型管片设计，以探究管片厚度的影响。

1.2 相似关系

综合考虑模型试验的可靠性、经济性和灵活性，选定模型试验以几何相似比1∶10，容重相似比1∶1。根据三大相似定理确定了相关物理、力学量的相似关系，详细的设计方法可参考黄大维研究成果[21-22]，模型试验相似常数如表1所示。

表1 模型试验相似常数

1.3 模型管片

试验通过测试收敛变形判断管片的抗变形能力，因此，模型管片的弯曲变形能力是模型设计的主要控制指标。为实现对这一指标控制，需同时对管片材料、厚度和接头进行设计。此外，考虑错缝拼装对管片受力的影响，采用三环错缝的方式拼装模型管片。

1.3.1 模型管片材料

选用尼龙66作为模型管片材料，材料弹性模量为2.7GPa，与C50混凝土弹性模量的相似比为1∶12.78，与几何相似比1∶10接近。尼龙66材料弹性较好，在试验荷载下始终处于弹性变形阶段，因此，本试验也主要反映管片材料在弹性阶段的行为。

1.3.2 模型管片厚度

通过对相似换算后的模型管片厚度进行修正，可保证结构的弯曲变形完全满足相似比要求1∶1。厚度修正方法参考文献[21]。计算结果表明，厚度相似常数满足1∶9.22时，模型与原型的弯曲变形相似比达到1∶1，同时两种次要关注的变形即轴向变形与剪切变形相似比分别达到1∶0.85和1∶0.71。换算后的各原型和模型管片厚度如表2所示。

1.3.3 纵缝接头模拟

拼装管片环纵缝接头位置抗弯刚度的削弱导致其力学性能不同于均质圆环。管片接头刚度对结构内力与变形存在较大影响[23-24]。本模型试验采用开槽法模拟管片纵缝接头，通过抗弯刚度等效原则确定开槽深度。采用开槽的方式模拟管片纵缝接头，已有数值模拟和试验方法证实可较好模拟纵缝接头的刚度衰减，且影响因素简单明确[20-22]。开槽后的模型管片如图1所示。开槽段壁厚如表2所示，针对不同内径φ和厚度T的管片，考虑接头刚度在正、负弯矩下差异，计算出不同的厚度。

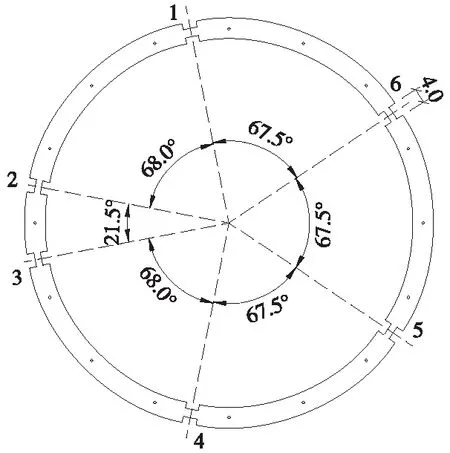
图1 模型管片纵断面(单位：mm)

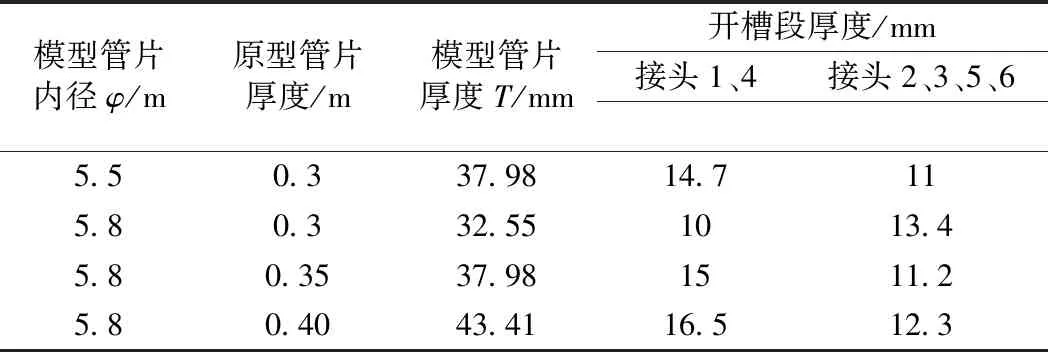
表2 模型管片、纵缝接头开槽尺寸

1.3.4 环缝接头模拟

本模型试验只模拟横向变形，近似地认为各环管片的横向变形一致，且不考虑隧道纵向不均匀沉降。因此，相邻管片环之间不传递弯矩，管片环间的纵向连接螺栓不承受拉力，故纵向连接螺栓无须采用螺母。本次模型隧道管片环之间的连接螺栓采钢棒代替，钢棒直径约4 mm，钢棒长约40 mm，这使得缝接头具有足够大的刚度，相邻管片环不发生错动。

1.4 试验装置与加载方案

1.4.1 模型试验装置

试验装置主要由环形加载装置和采集系统两部分构成。加载装置实物如图2所示，整体尺寸为1.65 m×1.65 m×1.5 m，采用卧式加载，通过环形反力架和千斤顶提供推力。环形加载装置上安设2圈液压千斤顶，每圈安设24台千斤顶，共48台。48台液压千斤顶配备油路和高精度液压油泵，其推力经由24个持荷梁将荷载传递至管片。

采集系统主要包含1台东华3816N采集仪，4台直线位移传感器以及一系列应变片。位移传感器和应变片布设如图3所示，以拱顶为0°，在中环管片内侧沿顺时针方向每隔一定角度布置应变片，共布设10处应变片，外侧拱顶位置布置1处。同样以拱顶为起始角，沿顺时针方向每90°布设1台0.001 mm精度的直线位移传感器测量管片径向变形。应变片和位移传感器的测量位置均在中环中部。

图2 试验装置

图3 应变和位移测点布置

1.4.2 加载方案

试验装置可实现环向24点同时加载。将24处加载点划分为荷载分区P1、P2和P3，如图4所示，分别由3组液压千斤顶单独控制。P1有6处加载点，分别位于拱顶和拱底，用于模拟隧道顶部所受的竖向荷载和隧道底部所受的地基反力；P2有10处加载点，分别位于拱腰两侧，用于模拟隧道所受的侧向压力；P3有8处加载点，用于模拟过渡压力，取P1和P2的均值。

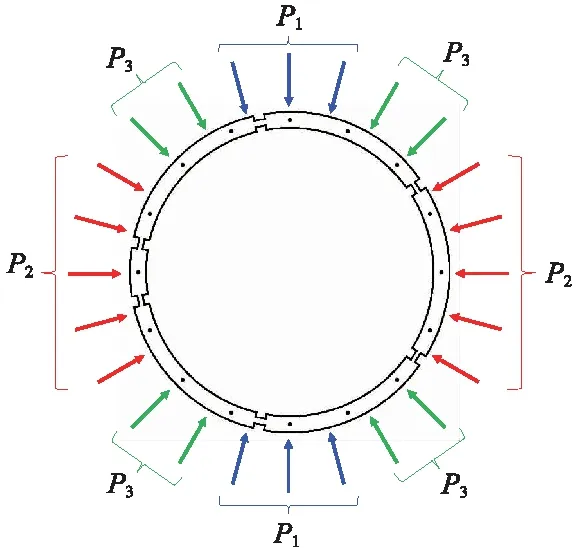
图4 加载点分布

根据原型隧道所处地质条件，选取中埋和深埋两处典型断面，根据土柱理论计算得到上方的垂向土压力分别为270 kPa和350 kPa。依据相似关系1∶10得到对应的模型试验荷载P1分别为27 kPa和35 kPa(目标荷载)，侧向压力系数则根据地勘报告取0.6。试验过程分为加载和超载两个连续阶段：①加载阶段内，P1分5级由0加载至目标荷载，这期间P2保持为0.6倍P1，P3控制为P1和P2的均值；②超载阶段内，保持荷载P2不变，P1则以原有的分级加载速率加至目标荷载两倍，这期间P3依旧保持为P1和P2的均值。

2 试验结果分析

2.1 管片整体变形

对管片整体变形展开分析，将加载过程中模型管片的收敛情况根据相似关系1∶10换算为原型管片的收敛值，竖向和水平收敛情况如图5所示(收敛以管片该方向尺寸收缩为负，该方向尺寸扩大为正)。由图可知，进入正常加载阶段，管片即出现竖向收敛、水平向扩张的“横鸭蛋”变形，这一阶段内累计收敛随荷载逐级缓慢增大。进入超载阶段后，管片收敛迅速增大，其增大趋势随荷载等级逐渐加快。以深埋工况，内径5.8 m、厚度0.35 m管片为例，加载至正常设计荷载时管片的累计竖向、水平向收敛分别达到7.35 mm和5.29 mm，而超载结束时管片累计竖向、水平向收敛分别达到31.77 mm和26.84 mm，相比于正常加载结束时分别增大了332.24%和407.37%。此外，管片尺寸和厚度对其收敛值存在影响：管片厚度均为0.35 m的情况下，增大内径导致管片累积收敛值增大；而在管片内径均为5.8 m的条件下，增大管片厚度则一定程度上抑制了变形。

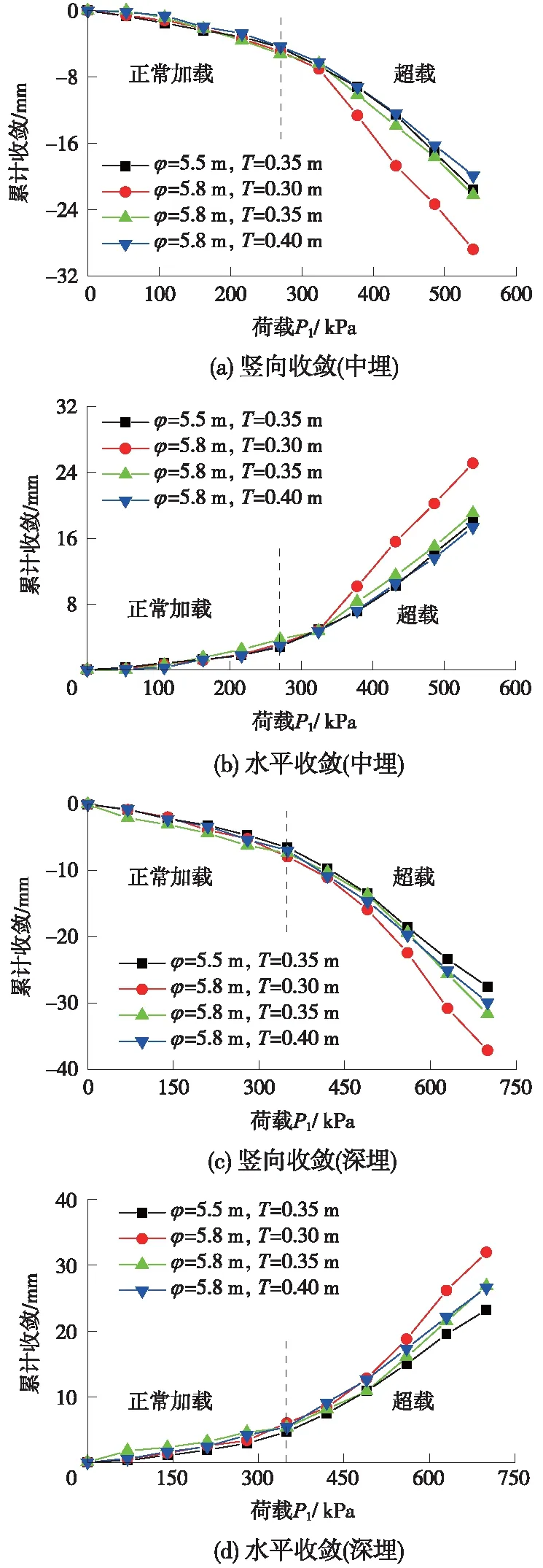
图5 管片累计收敛随荷载变化曲线

由于盾构隧道管片衬砌是圆环结构，其受载时易出现“横鸭蛋”变形。因此，采用椭圆率a量化其变形程度[25]可以同时反映竖向与水平向累计收敛程度，a由变形后管片长轴、短轴的差值除以管片初始外径计算得到。中埋和深埋条件下，不同内径、厚度管片的椭圆率随P1变化情况如图6所示。与收敛发展规律一致，在正常加载阶段，管片变形发展较缓慢，且不同内径、厚度的管片变形量值相近。而在超载阶段内，随P1/P2荷载比的迅速增长，管片变形趋于明显且呈非线性发展趋势。采用椭圆率可更显著区分出管片尺寸对整体变形的影响，就总体趋势而言，厚度相等条件下，管片内径增大导致其椭圆率趋于明显；而在管片内径相等情况下，增大管片的厚度可明显降低椭圆率。

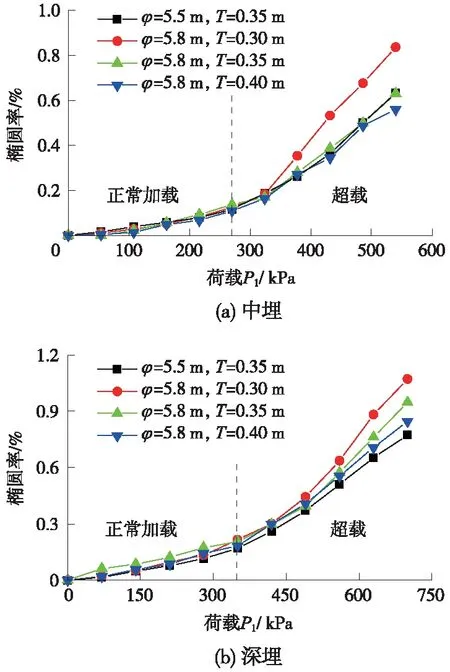
图6 管片椭圆率随荷载变化曲线

为定量反映不同内径、厚度管片间变形量的区别，将各管片在超载结束时的累计收敛和椭圆率绘制如图7所示，将所有管片的变形相对内径5.8 m、厚度0.35 m管片的变形值做归一化。以深埋条件的椭圆率为例，对于厚度为0.35 m的管片，内径由5.8 m降低至5.5 m导致其椭圆率较原先降低了19%；对于内径同为5.8 m的管片，厚度由0.35 m减小至0.3 m导致其椭圆率较原先增大了13%，而厚度由0.35 m增大至0.4 m导致其椭圆率较原先降低了11%。由此可见，增大管片内径会显著降低管片整体刚度，降低了其抗变形能力。而矩形截面管片的抗弯刚度EI与管片厚度的三次方呈正比，因此，增大管片厚度可明显提高管片的抗弯刚度，从而降低其整体变形[26]。

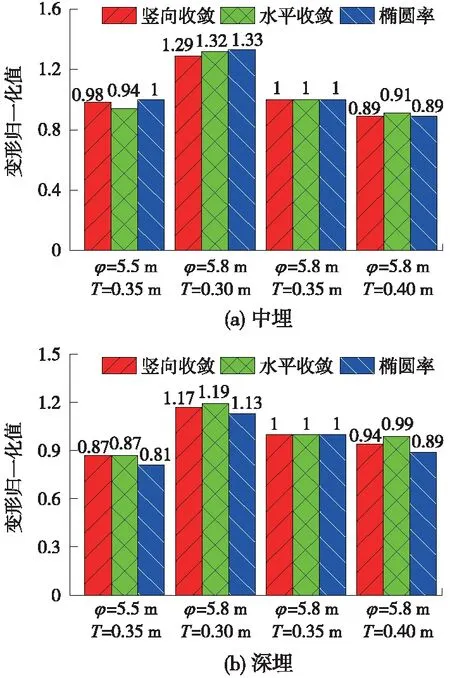
图7 内径、厚度对管片变形影响

2.2 管片局部应变

对管片应变展开分析，将加载过程中模型管片的应变根据相似关系1∶1换算为原型管片应变值(应变以受拉为负)。将超载结束时的管片内侧应变分布绘制如图8所示。由图8可知，最大拉应变产生于拱顶、底位置。以中埋工况为例，对厚度0.35 m的管片，内径由5.5 m增大至5.8 m，超载结束时拱顶的累计拉应变绝对值增大了36.51%，拱底累计拉应变绝对值增大了9.44%。而对于内径同为5.8 m的管片，厚度由0.4 m减小至0.3 m，超载结束时拱顶的累计拉应变绝对值增大了17.17%，拱底累计拉应变绝对值增大了12.11%，左、右拱腰的内测累计压应变分别增大了55.45%和93.27%。大部分测点应变值均随管片厚度增大而下降，应变沿环向分布趋于均匀。

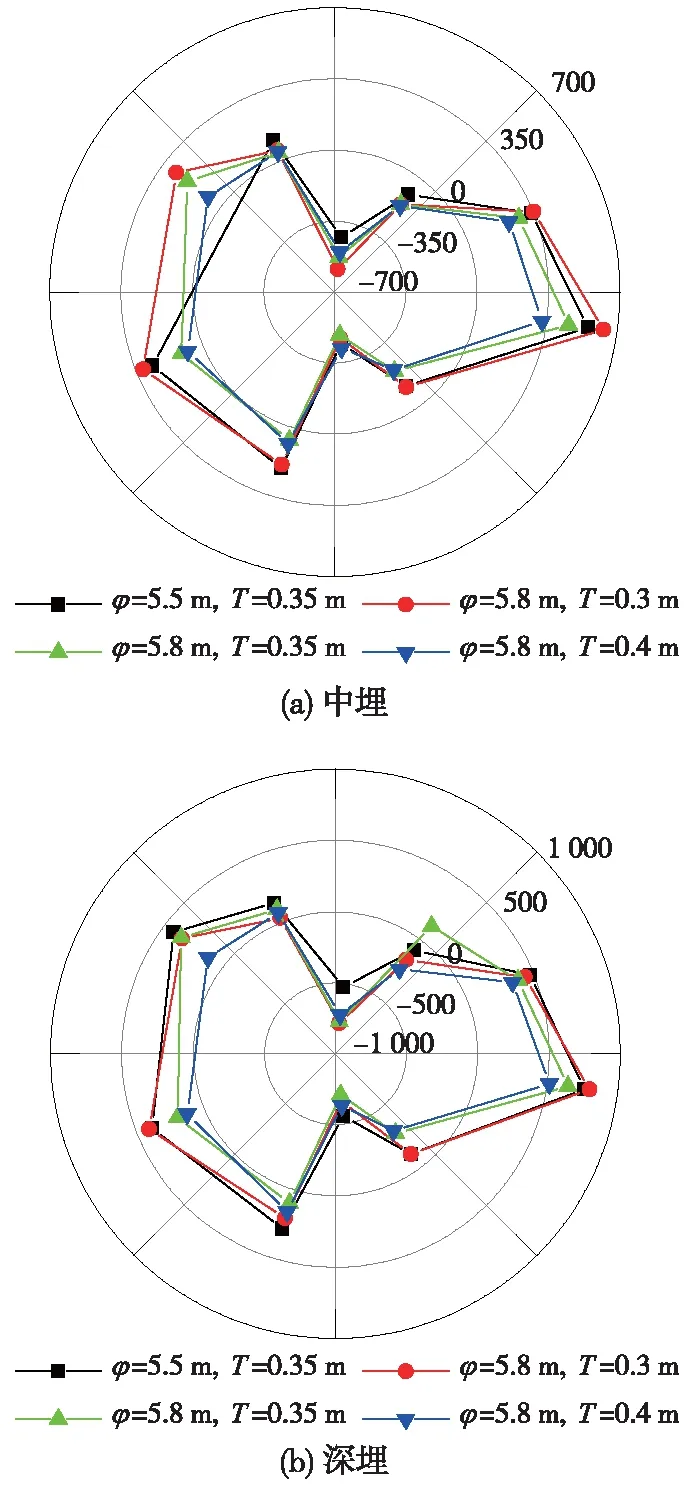
图8 管片内侧表面应变分布(单位：με)

混凝土管片的受拉强度远小于受压强度，实际工程中应关注其管片内表面最大拉应变，将试验获得拱顶/底最大拉应变整理如表3所示。从管片应力/应变的角度出发进行分析，在保持管片厚度不变的前提下，增大管片内径将导致其最大拉应变增大。以深埋工况为例，管片厚度均为0.35 m的条件下，内径由5.5 m增大至5.8 m导致其最大拉应变增大了38.28%。与此同时，增大厚度可降低管片表面的拉应变，在中、深埋条件下，增大管片厚度由0.3 m至0.4 m可将最大拉应变分别降低14.65%和7.28%。说明，若面临顶部超载工况，单纯增大内径可能导致混凝土管片受拉侧开裂破坏，对管片结构受力不利，为降低管片的拉应变，可适当增大其厚度。

表3 管片内测最大拉应变 με

2.3 管片结构弯矩

基于在拱顶管片外侧布设的应变片，通过式(1)计算管片拱顶所受弯矩M[27]。

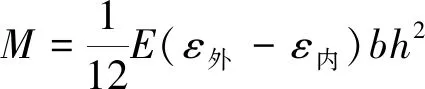
(1)

式中，E为模型管片弹性模量；ε外为管片外侧应变；ε内为管片内侧应变；b为模型管片宽度；h为模型管片厚度。将模型管片弯矩依据相似关系1∶1 000换算为原型管片弯矩。绘制中埋、深埋条件下，拱顶弯矩随P1的发展情况，如图9所示。由图9可知，进入正常加载阶段内，拱顶就开始产生负弯矩，即管片内测受拉，且弯矩发展较缓慢。进入超载阶段后，弯矩较原先更迅速发展。以深埋工况为例，加载结束时，在管片厚度均为0.35 m的条件下，内径由5.5 m扩大至5.8 m导致拱顶弯矩由451.43 kN·m增大至609.43 kN·m；而在管片内径均为5.8 m的条件下，管片厚度由0.3 m增大至0.35 m和0.4 m导致拱顶弯矩由439.19 kN·m增大至609.43 kN·m和746.39 kN·m。中埋工况下，弯矩同样随管片内径和厚度增大呈现增大趋势。

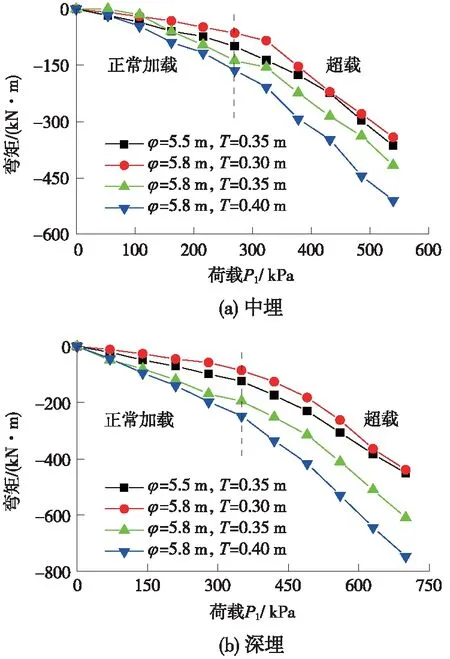
图9 管片拱顶弯矩随荷载变化曲线

除弯矩增大外，偏心距也是评价管片受力的重要指标。图10展示了中埋、深埋超载工况下，拱顶弯矩、偏心距在加载结束时的对比情况。由图10可知，厚度不变条件下，增大管片内径不仅导致其变形增大，且导致其最大拉应变/力、弯矩、偏心距均增大，使得管片处于更不利的受力状态。在管片内径保持不变的前提下，增大管片厚度虽然导致弯矩和偏心距增大，然而图8、表3表明结构的应变/应力值降低，因而，管片厚度增大并不会导致更不利的受力状态。因此，实际工程中面临需增大管片内径的情况时，可通过增加管片厚度避免其进入偏于危险的受力状态。

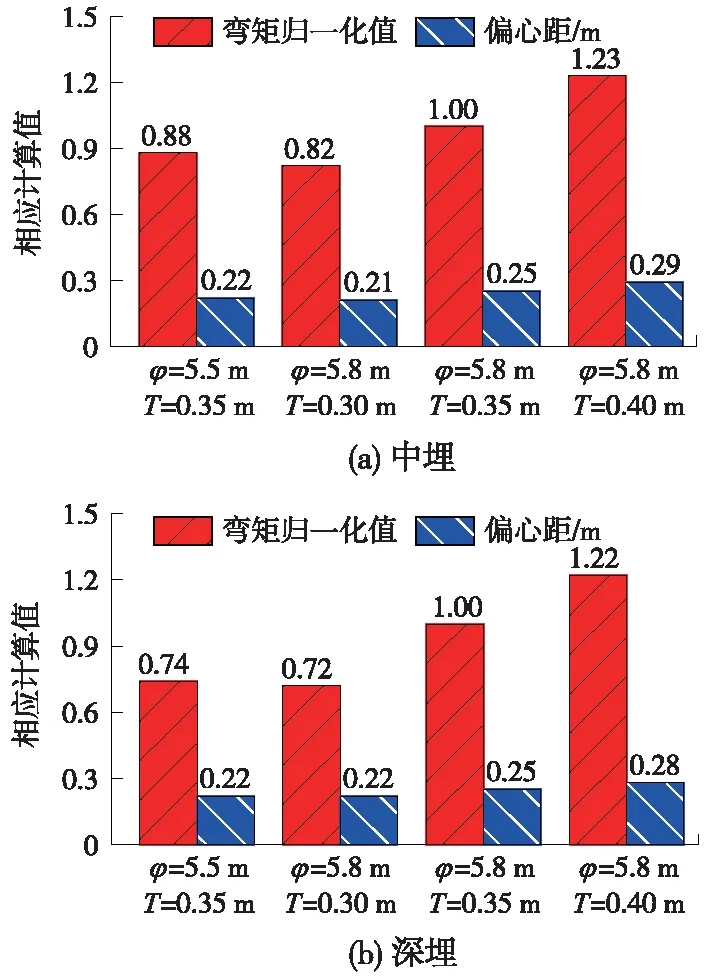
图10 内径及厚度对管片拱顶弯矩、偏心距影响

3 结论

针对5.8 m内径隧道管片在南京地区的首次应用，采用几何相似比1∶10的模型试验，从整体变形、局部应变和结构弯矩3个方面，定量地研究了盾构隧道内径扩增对其结构抗变形能力的影响，探讨了内径扩增后的管片厚度优化，得到以下结论。

(1)正常加载阶段隧道管片模型的整体变形、应变和内力增速缓慢；超载阶段管片整体变形、应变和内力迅速增加，且增速呈逐级加快趋势，即管片更容易在超载阶段内发生破坏。

(2)管片厚度不变的前提下，增大管片内径会降低结构抗变形能力，在超载情况下将导致更大的收敛变形；此外，增大管片内径导致更大的拉应变、弯矩和偏心距，使管片处于更不利的受力状态；深埋工况下，管片内径由5.5 m扩增至5.8 m导致超载条件下管片的水平、竖向收敛值增大了14.94%，最大表面拉应变增大了38.28%，拱顶弯矩增大了35.14%。

(3)增大管片厚度可一定程度上提高其结构抗变形能力，但其结构承受的弯矩和偏心距也随之增大；然而，厚度增加同时提升了其自身的抗弯刚度，使管片承受的最大拉应变/应力降低，管片整体处于更加安全的受力状态。

本次模型试验隧道内径由5.5 m扩增至5.8 m仅是略微增大，考虑到顶部超载和侧方卸荷等工况，可经过经济技术比选后适当增大管片厚度，以保证其结构抗变形能力。若面临更大幅度的内径扩增，则需考虑辅以钢环结构补强、土体注浆加固等措施。