不同内部结构类型对盾构隧道纵向力学性能的影响

王均勇,封 坤,孙文昊,鲁选一,郭文琦,漆美霖

(1.中铁第四勘察设计院集团有限公司,武汉 430063； 2.水下隧道技术国家地方联合工程研究中心,武汉 430071； 3.中国市政工程中南设计研究总院有限公司,武汉 430103；4.西南交通大学交通隧道工程教育部重点实验室,成都 610031)

引言

盾构隧道纵向变形过大导致管片环缝错台、张开，进而引发开裂、渗漏水的问题成为近年来影响盾构隧道正常运营的难题之一[1]，探明盾构隧道纵向结构的力学性能刻不容缓。

目前，对于盾构隧道纵向力学性能的研究主要有理论解析、数值计算、模型试验3类。在理论解析方面，廖少明[2]考虑了剪切荷载的作用，对盾构隧道纵向刚度求解进行了修正；徐凌[3]引入环缝影响系数，提高了纵向刚度理论求解的普适性；张文杰等[4]在纵向刚度求解中引入横向刚度的影响，提出了广义盾构隧道纵向等效连续化模型；耿萍等[5]同时考虑了轴力和弯矩对纵向弯曲变形的影响，提出了5种弯曲模式，并在经典志波模型的基础上，建立盾构隧道纵向等效抗弯刚度计算模型；张勇等[6]基于T-P模型推导了地面堆载作用下盾构隧道纵向变形的解析解。在数值计算方面，杨茜等[7]通过地层-结构模型研究了下卧土层性能和上方局部荷载作用对隧道沉降变形的影响；王金龙[8]通过ANSYS有限元计算软件建立三维数值模型探讨了埋深、水压、地层及穿越刚性结构物等因素对盾构隧道纵向力学性能的影响；张旭[9]通过建立三维有限元模型，对土体结构性、土层参数、水土耦合效果等方面对隧道纵向受力变形的影响进行了研究；郭文琦等[10]建立壳-弹簧模型研究了二衬厚度对盾构隧道纵向力学行为的影响；罗文林等[11]通过现场监测数据，建立数值模型反分析了隧道纵向弯曲刚度。在模型试验方面，余占奎[12]基于上海地铁盾构隧道，研究了拼装方式对盾构隧道纵向力学性能的影响；何应道[13]以广深高速铁路狮子洋水下隧道为原型，采用轴向等效刚度模型模拟了隧道在软弱匀质地层、软硬交界地层等多种复杂条件下隧道的沉降规律；何川等[14]采用等效刚度模型，以聚氨酯板和PVC板模拟单层管片衬砌，在衬砌内部浇入石膏模拟结构内衬，探讨了单、双层衬砌隧道纵向沉降与弯矩的变化关系；叶飞等[15]以有机玻璃作为管片模型材料，采用双点加载的方式探讨了盾构隧道纵向刚度有效率的取值；耿萍等[16]通过振动台模型试验，针对盾构隧道穿越软硬交界地层、联络横通道、纵向接头等抗震薄弱部位开展了系列研究。

随着盾构工法与盾构设备的成熟，盾构隧道正朝着超大直径方向发展[17]。在此背景下，盾构隧道内部结构的形式也随着隧道直径增加愈发多样[18]。过去盾构隧道设计中并未作为受力构件考虑的内部结构能否改变超大直径盾构隧道的纵向力学性能值得探讨与研究。鉴于此，以济南黄河隧道与武汉两湖隧道(东湖段)为工程依托，利用大型有限元软件ABAQUS建立数值计算模型，分析不同内部结构类型对隧道纵向力学性能的影响。

1 盾构隧道内部结构型式

根据不同的功能用途盾构隧道可分为公路隧道与铁路隧道。在两种类型的中小型隧道中目前最为普遍使用的是单管单层结构形式，该结构形式设置一层车道板用于通车，其他空间通过预制或现浇的墙板分隔成若干隧道正常运营所需的不同工作腔室。在大型隧道中则常采用单管单层双线结构形式，该形式在隧道底部设置预制构件，构件的内部作为工作腔室，构件的顶部铺上车道板，同时被中隔墙分隔为两车道。随着超大型盾构隧道的发展，单管双层结构成为目前国内外逐步推广应用的结构形式[19]。根据已有隧道修建资料，单管双层结构可分为3类。第一类是公路型内部结构，该类型上、下层均为公路交通；第二类是轨道型内部结构，该类型上、下层均为轨道交通；第三类是公轨合建型内部结构，该类型通常上层用于公路交通，下层用于轨道交通。表1为国内外典型隧道的内部结构形式统计。由于轨道型内部结构的案例目前在国内并未出现，故以公路型内部结构与公轨合建型内部结构展开研究。

2 依托工程概况

2.1 工程概况

济南市济泺路穿黄隧道位于济南市城市中部，全长4.76 km，其中，盾构段长2.516 km。隧道最大埋深50 m，最大水位水压力达0.65 MPa，为国内跨越黄河最大直径盾构隧道，也是黄河上第一条公铁合用隧道。

表1 国内外盾构隧道内部结构统计

武汉两湖隧道工程(东湖段)主线线路全长约11.45 km，为单管双层公路隧道。隧道最大埋深42.5 m，最大水位水压达到0.46 MPa，隧址区岩溶发育，主要穿越强中风化泥岩。

2.2 管片衬砌

济南黄河隧道及武汉两湖隧道横断面如图1、图2所示，隧道其他参数见表2。

表2 隧道参数

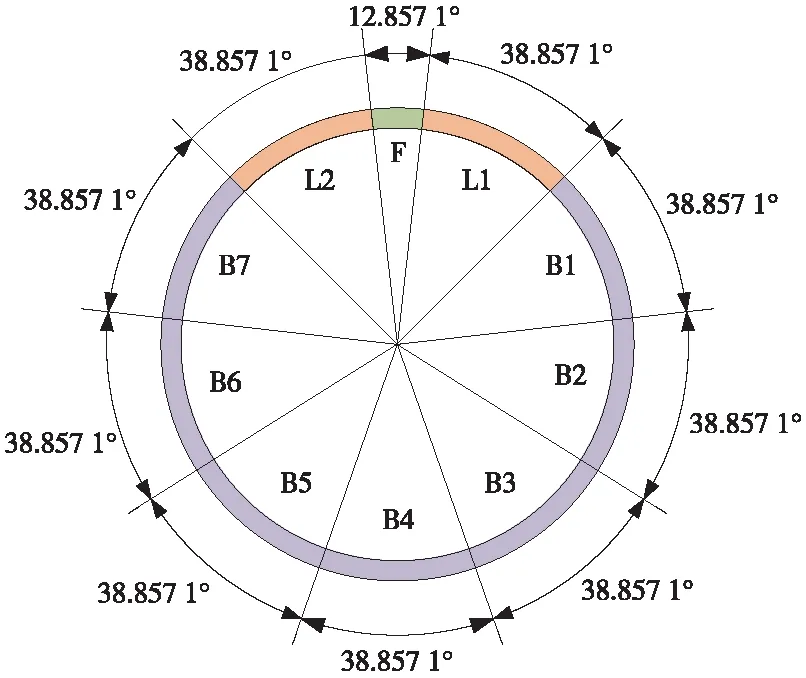
图1 济南黄河隧道管片横断面

图2 武汉两湖隧道(东湖段)管片横断面

2.3 内部结构

济南黄河隧道内部结构采用单管双层结构形式中的公轨合建形式，如图3所示。该内部结构幅宽2 m，中间为一个Π字形预制构件，构件中间的空间则作为地铁通车的轨道交通区域。Π形件两侧搭接预制车道板，与Π形件顶部共同作为上层的公路车道。内部结构与管片内侧之间浇筑混凝土形成非封闭二衬。

图3 济南黄河隧道内部结构示意

武汉两湖隧道(东湖段)内部结构采用单管双层结构形式中的双层公路形式，如图4所示。该内部结构幅宽6 m，下层采用Π形预制构件且两侧用素混凝土回填。为满足道路结构与盾构掘进同步施工的要求，下层立柱、上层车道板及牛腿采用现浇形式，待整个隧道施工完成后铺设路面层。

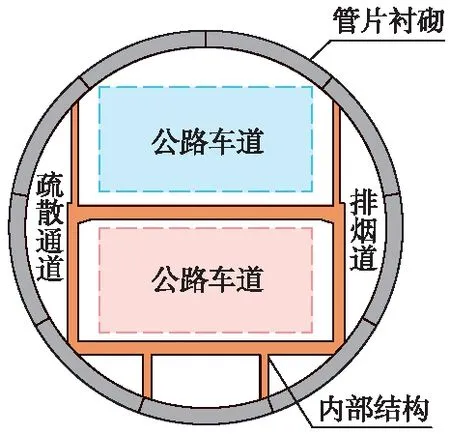
图4 武汉两湖隧道(东湖段)内部结构示意

3 数值计算模型

3.1 计算假定

由于盾构隧道是复杂的三维拼装结构，其数值计算模型具有高度的非线性，为减少计算成本，现做计算假定如下。

(1)由于盾构隧道接头位置较管片主体更薄弱，因此，盾构隧道接头较管片主体更先达到塑性阶段，以往研究通常是在钢筋混凝土管片的弹性阶段进行分析[20]，故本次将管片视为均质弹性材料，螺栓采用双线性本构关系。

(2)实际工程中内部结构具有搭接、现浇、植筋等多种连接。内部结构模型的建立忽略上述连接，将内部结构视为一均质整体。

3.2 模型概况

为尽可能反映盾构隧道的纵向力学特征，利用大型有限元软件ABAQUS建立了31环盾构隧道管片模型，如图5、图6所示。其中，管片及内部结构采用C3D8R实体单元，螺栓采用B31两节点空间线性单元。利用ABAQUS内嵌功能将螺栓两端嵌入管片实现螺栓与管片的连接。管片块与块以及环与环之间采用面-面接触，其切向行为采用罚函数设置摩擦系数为0.8，法向为防止发生穿透导致与实际情况不符设置为硬接触，管片与内部结构之间采用相同的相互作用。其他各项参数如表3所示。

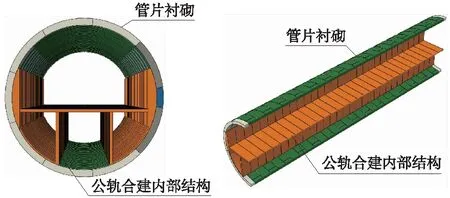
图5 济南黄河隧道数值计算模型

图6 武汉两湖隧道(东湖段)数值计算模型

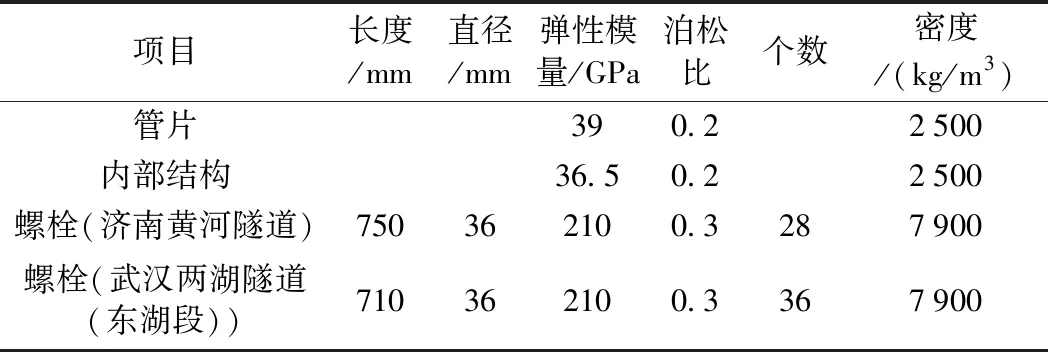
表3 模型参数

3.3 试验工况及加载方式

试验工况根据隧道拼装形式以及有无内部结构分为5种：通缝拼装形式无内部结构隧道、通缝拼装形式含内部结构隧道、错缝拼装形式无内部结构隧道、错缝拼装形式含内部结构隧道及匀质圆环。

力学模型采用荷载-结构模型，如图7所示，加载方式类似于简支梁，隧道一端限制其Y、Z方向上的位移，另一段限制其X方向上的位移，隧道中间一环作为加载环承受集中力来等效弯矩的作用，力的大小为500～2 500 kN，每级增加500 kN。

图7 隧道模型加载方式示意

4 结果分析

4.1 隧道纵向刚度分析

4.1.1 隧道纵向变形分析

现规定隧道轴向为坐标横轴，且第一环管片为零点。纵轴为隧道竖向位移，竖直向下为负值。以集中力大小2 500 kN为例，将隧道最底部的竖向位移作为整个隧道的位移得到图8、图9。其中，曲线命名第一项为工程名称首字母缩写；第二项为拼装方式，TF表示通缝，CF表示错缝，YZYH表示匀质圆环；第三项表示是否考虑内部结构，考虑则标注NBJG。

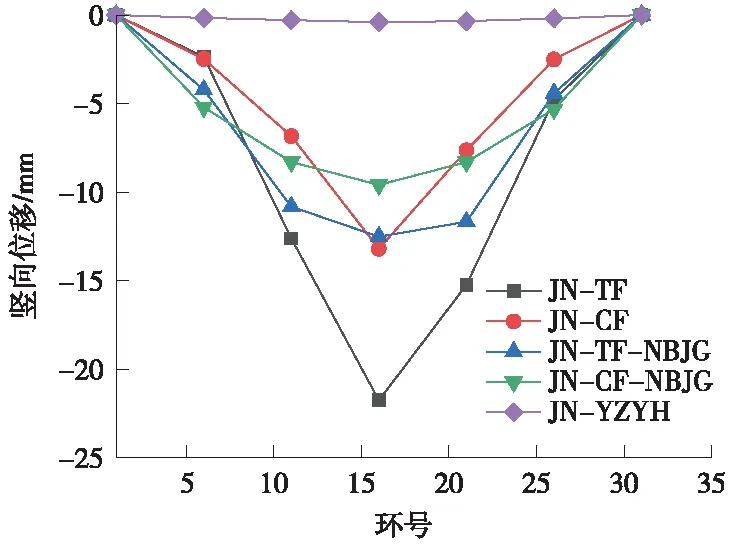
图8 济南黄河隧道纵向位移曲线

图9 武汉两湖隧道(东湖段)纵向位移曲线

从图中可以看出，两个隧道的变形规律相似，即跨中位移最大，并向两端位移减少，这与简支梁的变形规律类似。当考虑内部结构后，武汉两湖隧道(东湖段)位移曲线形状未发生较大变化，而济南黄河隧道位移曲线相比未考虑内部结构时更接近材料力学中梁的挠度曲线，这说明考虑公轨合建型内部结构隧道提高了盾构隧道在纵向上的结构连续性。

提取加载环底部位移作为隧道跨中位移得到图10、图11。从图中可以看出，考虑内部结构后隧道的竖向位移显著减小。对于济南黄河隧道考虑内部结构后，通缝拼装形式隧道跨中位移减小了13.1%～39.3%，错缝拼装形式隧道跨中位移减少了10.5%～23.4%；对于武汉两湖隧道(东湖段)，通缝拼装形式隧道跨中位移减少了14.9%～28.4%，错缝拼装形式隧道跨中位移减少了11.1%～23.1%。从以上结果来看，内部结构能够显著提高隧道的纵向刚度。

图10 济南黄河隧道跨中位移曲线

图11 武汉两湖隧道(东湖段)跨中位移曲线

4.1.2 隧道纵向刚度有效率分析

根据已有计算盾构隧道纵向刚度有效率方法[15]，即

(1)

式中，η为纵向刚度有效率；(EI)eq为等效连续化模型的纵向刚度；EcIc为隧道实际抗弯刚度。结合挠曲线方程计算得到隧道的纵向刚度有效率，如图12所示。

由图12得知，济南黄河隧道在不考虑内部结构时，通缝拼装形式的纵向刚度有效率为0.014～0.019，错缝拼装形式的纵向刚度有效率为0.029～0.032。当考虑内部结构后，通缝拼装形式的纵向刚度有效率为0.017～0.031，较未考虑内部结构时提高了15.1%～64.8%；错缝拼装形式的纵向刚度有效率为0.032～0.042，较未考虑内部结构时提高了11.7%～30.6%。武汉两湖隧道(东湖段)在不考虑内部结构时，通缝拼装形式的纵向刚度有效率为0.03～0.034，错缝拼装形式的纵向刚度有效率为0.043～0.046。当考虑内部结构后，通缝拼装形式的纵向刚度有效率为0.036～0.048，较未考虑内部结构时提高了17.5%～39.6%；错缝拼装形式的纵向刚度有效率为0.048～0.059，较未考虑内部结构时提高了12.5%～30%。

通过上述结果分析可以看到，两种形式内部结构对通缝拼装隧道的纵向刚度有效率提升效果更显著，其中，公轨合建形式内部结构对通缝拼装形式隧道的纵向刚度有效率提高了50%以上。对于不同隧道拼装形式而言，公轨合建型内部结构对纵向刚度有效率的提升效果均优于双层公路型内部结构。

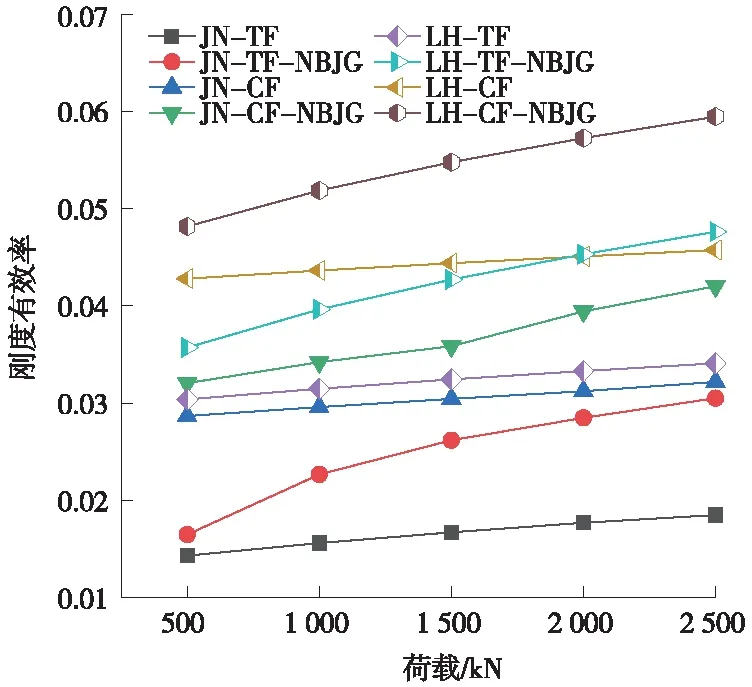
图12 隧道纵向刚度有效率

4.2 隧道内力分析

以错缝拼装为例，两个隧道在荷载为2 500 kN下MISES应力云图如图13、图14所示。

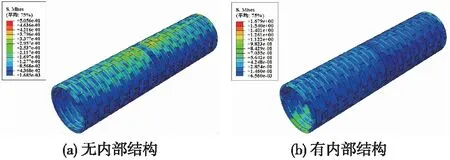
图13 济南黄河隧道错缝MISES应力云图(单位：MPa)

图14 武汉两湖隧道(东湖段)错缝MISES应力云图(单位：MPa)

从图13(a)、图14(a)中可以看出，两个隧道在错缝拼装形式下应力分布特点基本一致，且数值较大的MISES应力集中分布在拱顶处。济南黄河隧道拱顶处的MISES应力值在0.13～0.46 MPa范围内，且越靠近加载环位置的管片环其MISES应力值更大。同时，在加载环两侧的3环范围内由于弯矩传递效应还发生了应力集中现象。武汉两湖隧道(东湖段)在错缝拼装形式下，拱顶应力值为0.26～0.7 MPa，且上述济南黄河隧道中应力分布特点同样能够在武汉两湖隧道(东湖段)中体现。

考虑内部结构后，两个隧道的应力分布各自发生了不同变化。从图13(b)中可以看到，济南黄河隧道在考虑公轨合建内部结构后，管片应力值整体上减小，拱顶、拱肩、拱腰等位置的MISES应力值较未考虑内部结构时最大减小了50%以上。然而，其下层轨道交通运行区域内，即内部结构下侧两侧墙与管片连接位置之间，MISES应力值为0.42～0.98 MPa，较未考虑内部结构时的拱顶的MISES应力值大了40%～61.5%，说明该区域应力值较大，应考虑填充混凝土、加钢板等补强措施。

从图14(b)中可以看到，武汉两湖隧道(东湖段)在考虑双层公路内部结构后，管片的MISES应力分布规律与未考虑内部结构时基本一致，即拱顶处应力值较大。观察其MISES应力数值可以发现，管片应力较未考虑内部结构时减小了25%以上，这说明无论是公轨合建型内部结构，还是双层公路型内部结构均可起到承载作用。同时，双层车道内部结构显著减小了拱腰位置的MISES应力值。当未考虑双层公路内部结构时，隧道拱腰位置的MISES应力值为0.18～0.44 MPa，而当考虑内部结构后为0.09～0.36 MPa，减小了18%～50%。

从受力条件上来说，两种类型内部结构均能够起到分担荷载的作用，但公轨合建型内部结构会导致管片拱底一定范围内的应力值过大，相较之下双层车道内部结构未发生管片出现较大范围应力增加现象，因此更有利于受力。

4.3 内部结构变形受力分析

4.3.1 内部结构纵向变形分析

图15、图16为济南黄河隧道和武汉两湖隧道(东湖段)内部结构的纵向位移云图。从图中可以看出，两种类型内部结构跨中位移最大，向两端逐渐减小，即其内部结构的变形与管片变形规律一致，符合梁的变形规律。从图15可以看出，公轨合建内部结构在纵向上的变形主要包括错台与张开，隧道最大竖向位移为8.9 mm，而内部结构发生了向上0.68～1.5 mm的位移。从图16中可以看出，双层公路内部结构在纵向上发生的变形同样为错台与张开，最大竖向位移为8 mm，但在隧道两端并未出现向上的位移。

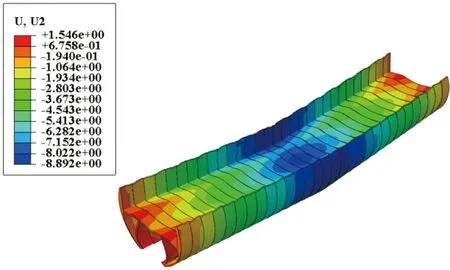
图15 济南黄河隧道内部结构纵向位移云图(单位：mm)

图16 武汉两湖隧道(东湖段)内部结构纵向位移云图(单位：mm)

4.3.2 内部结构横向变形分析

图17、图18为济南黄河隧道与武汉两湖隧道(东湖段)内部结构横向位移云图。

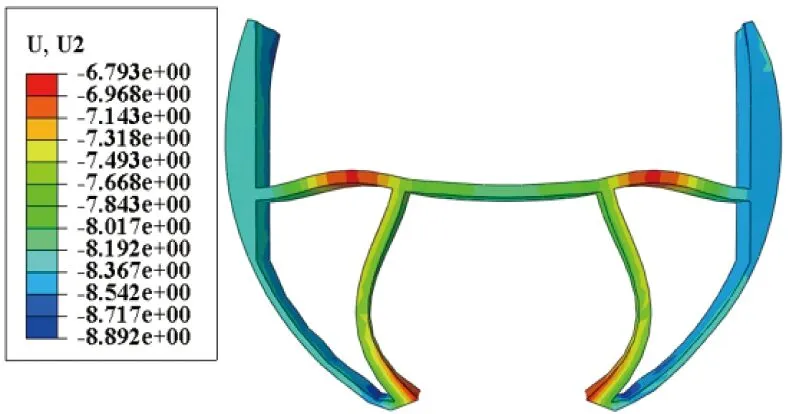
图17 济南黄河隧道内部结构横向变形云图

图18 武汉两湖隧道(东湖段)内部结构横向变形云图

从图17可以看出，济南黄河隧道上层车道板发生了形如“M”状变形，左跨与右跨车道板发生了向上的弯曲，中跨车道板向下弯曲，且中跨竖向位移最大，为8.892 mm。同时，内部结构下层轨道交通区域侧墙发生了向外的弯曲，侧墙上下两端出现了扭转，整个侧墙结构受到弯扭作用。

从图18中可以看出，双层公路内部结构上层车道板较公轨合建内部结构的位移小，同时并未出现位移向上的现象。然而，下层车道板跨中出现了向上的位移，整个车道板呈开口向下的弧形。观察双层公路内部结构上层车道侧墙与下侧Π形件侧墙，发现其受力特征与公轨合建内部结构侧墙一致，均受到了弯扭作用。

4.3.3 内部结构受力分析

图19、图20为不同类型内部结构的MISES应力云图。

图19 济南黄河隧道内部结构MISES应力云图(单位：MPa)

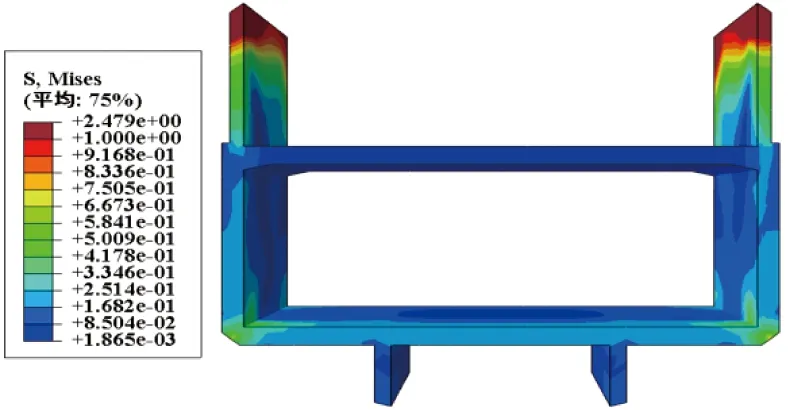
图20 武汉两湖隧道(东湖段)内部结构MISES应力云图(单位：MPa)

从图19可以看出，公轨合建内部结构车道板处的MISES应力值较小，为0.27～0.77 MPa。相比之下，下层侧墙和非封闭二衬部分出现了应力集中现象，特别是侧墙与非封闭二衬之间的连接部位MISES应力值最大达到18 MPa，而下层侧墙与非封闭二衬的厚度与其他位置相比较薄，因此，该部位考虑采用对应的补强措施。同时，上层侧墙与管片连接处MISES应力值在1～2 MPa，需注意现浇侧墙时的施工质量问题。

从图20可以看出，双层公路内部结构上层车道板MISES应力值为0.001 9～0.17 MPa；下层车道板MISES应力值为0.085～0.33 MPa，且在其与侧墙连接处应力值达到0.67 MPa，应力值显著大于上层车道板。同时，上层车道侧墙与盾构管片连接位置也出现了应力集中现象，应力最大达到2.5 MPa。

综合上述两种内部结构受力特点，可以得到盾构隧道纵向受力时，其内部结构自身各部位的连接点及内部结构与管片的连接部位是受力关键点。现有连接方式主要有搭接、现浇、植筋、灌浆套筒等，不同的连接方式也将导致连接点的刚度不同，对整个内部结构受力也会有所影响，应根据具体工程实际谨慎选择。

5 结论

以济南黄河隧道和武汉两湖隧道(东湖段)为工程背景，建立了31环隧道纵向三维模型，对比讨论了公轨合建型内部结构与双层公路型内部结构对盾构隧道纵向力学性能的影响，得到主要结论如下。

(1)内部结构能够显著提高隧道的纵向刚度。隧道考虑公轨合建型内部结构后，跨中位移最大减小了39.3%，考虑双层公路内部结构后，跨中位移最大减小了28.4%。

(2)隧道考虑公轨合建内部结构后，通缝拼装形式的纵向刚度有效率提高了15.1%～64.8%，错缝拼装形式的纵向刚度有效率提高了11.7%～30.6%；隧道考虑双层公路内部结构后，通缝拼装形式的纵向刚度提高了17.5%～39.6%，错缝拼装形式的纵向刚度有效率提高了12.5%～30%。两种形式内部结构对通缝拼装形式隧道的纵向刚度有效率提升效果更显著，公轨合建型内部结构对刚度的提升效果优于双层公路型。

(3)内部结构在盾构隧道纵向上受力起到承载作用。当隧道考虑公轨合建型内部结构后，管片MISES应力值可减小50%以上；当隧道考虑双层公路型内部结构后，管片MISES应力值可减小25%以上。

(4)两种类型内部结构在纵向上的变形主要以错台、张开为主，同时内部结构侧墙均受到弯扭的作用。

(5)内部结构自身连接部位及内部结构与管片之间的连接点应力值较大，且有应力集中现象发生，在实际工程中应谨慎选择连接方式。