研读教材试题,提升中考解题能力
——一道甘肃中考压轴题的命题与反思
2022-11-15颜天伦
颜天伦
(福建省晋江市毓英中学,福建晋江,362251)
二次函数的综合题是中考的重点和难点,因为二次函数的图象和性质的研究利用的是从简单到复杂、从特殊到一般的方法,这些方法是认识事物规律的重要方法,是进一步学习的基础;其次,利用二次函数解决实际问题是对学生实践能力考查的良好载体,无论从基础性还是综合性方面都能赢得命题专家的青睐,因此教师要吃透学情和教材,研究考情,学会从“最近发展区”开始,逐步引导学生达到中考能力要求的制高点,这样才能无往而不胜.
1 试题呈现
例1(2020年甘肃省定西市中考数学试卷第28题)如图1,在平面直角坐标系中,抛物线y=ax2+bx-2交x轴于A,B两点,交y轴于点C,且OA=2OC=8OB.点P是第三象限内抛物线上的一个动点.

图1
(1)求此抛物线的表达式;
(2)若PC//AB,求点P的坐标;
(3)连接AC,求△PAC面积的最大值及此时点P的坐标.
2 导问结合,分析探究
2.1 回归基础,立足教材
立足教材是中考命题的一个原则,给学生一个以退为进的探究平台.
源题:(义务教育教科书九年级上册第57页综合运用题)根据下列条件,分别确定二次函数的解析式:
(1)抛物线y=ax2+bx+c过点(-3,2),(-1,-1),(1,3);

教师:如何求出二次函数的解析式?
学生1:设出二次函数的解析式y=ax2+bx+c,然后用待定系数法求解.
教师:回答得很好!就是用待定系数法,请同学们细心地代点列式.

教师:解答正确!注意用消元方法和转化的思想求解,熟练运算,要求结果准确无误.
教师:第(2)问中抛物线y=ax2+bx+c经过哪三点?
教师:题设虽然没有直接给出抛物线经过的三点,但这位同学善于抓住“与y轴交点”等关键字眼,能敏锐地洞察出三点的坐标,真棒!你会求出解析式吗?
教师:不错不错!在解答过程中一定要感受到待定系数法的实质就是运用方程思想.
2.2 类比思考,求同存异
教师:本题中如何求出抛物线经过的三点?切入点在哪里?
学生5:因为抛物线交y轴于点C,所以先求出C点的坐标,再根据OA=2OC=8OB,求得A,B两点的坐标.
教师:是这样的!切入点或者说突破口就是“抛物线交y轴于点C,其纵坐标即x=0时对应的y=-2”.
2.3 方程思想,化难为易
教师:点C是一个定点,已知PC//AB,告诉你一个怎样的数学事实?
学生6:OC等于点P到AB的距离,即点P的纵坐标和点C的纵坐标相等.
教师:能通过观察发现一个几何等量关系,太好了!如何求出点P的横坐标?

教师:反思我们求解的困难在哪里?两条平行直线间的距离相等,其实你画出AB平行的直线y=-2后,直观理解为此直线与抛物线的交点也可以.
2.4 由浅入深,循序渐进
教师:连接AC,因为没有一个直接求三角形的面积的条件是已知的,所以要求△PAC面积,你会想到什么?
学生8:采用分割法.
教师:对!这就是今后我们遇到求抛物线内接三角形面积时应该掌握的方法之一,如何分割求面积?
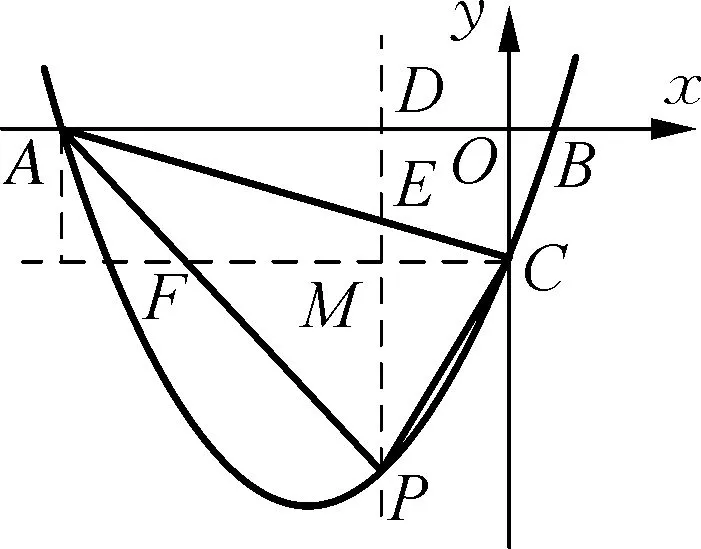
学生9:过点P作x轴的垂线,垂足为D,交线段AC于点E.这样把△PAC分割为两个三角形△APE和△PEC.
教师:分割得很好.依以往解题经验,两个三角形的底和高分别是什么?
学生10:过点C作CM⊥PE,M为垂足.这样就找到了△PEC的高CM,由于CM=DO,所以两个三角形有同底PE,高分别是AD和OD.

图2
教师:棒极了!求解线段长时必须设法把它化归到(或构造)某个平面图形中,或者尽可能转化在容易求出线段长的平面图形中,然后去求解.想一想:点P的直角坐标如何设?
教师:设得好!请问m的取值范围是什么?
学生12:-4 教师:点E的坐标如何求? 教师:上述的这些推演都是为求出两个三角形的底和高作铺垫.想一想:此问题中,三角形的底和高分别是什么? 教师:推演方法完全正确.接下来点P的坐标如何求? 教师:至此我们在教材内容基础上,采用分割的方法求出了面积目标函数,进而利用二次函数求最值的方法完成目标任务.问题综合性强,内涵丰富,思维量大,选拔功能不言而喻. 由于学生的知识结构、认知水平、能力大小不一,所以从审题到解题方法的运用都千差万别,使用的方法不可能整齐划一,总是繁简有别,所以在解题教学中,培养灵活运用知识分析求解问题的能力,尤其是准确而又迅速地解决问题的能力很重要. 视角一 教师:过点C作AB的平行线分割三角形,又如何来布列面积目标函数? 学生17:此时过C的平行线CF把△PAC分割为两个三角形△ACF和△PCF. 图3 教师:很好!请继续讲. 学生18:先求出直线AP的解析表达式,再将y=-2代入求得点F的坐标. 教师:请大家做一做,然后说出结果. 学生19:设直线AP的解析式为y=kx+b,则将点A(-4,0)代入,得b=4k,即y=k(x+4). 教师:请写出△PAC的面积的表达式. 教师:运算推理正确.从面积结果看还需求出线段FC和PD的长,如何求出它们的长? 教师:得出这两个结果,运算量都很大,表现出同学们极大的耐力和运算能力.请继续进行演算. 教师:从过程来看,由于直线AP不好确定,进而点F不好确定,尤其是点P的坐标的难以确定,运算量比较大,容易出错.与沿平行y轴的直线分割的思维相比较复杂. 视角二 教师:在直角三角形AOC中能否求出AC=? 教师:殊途同归,如何求△PAC面积? 教师:现在三角形的一边长AC是定值,要使△PAC面积最大,只需△PAC底边AC上的高最长,即点P到AC的距离最大.这个过程中用到了一个点到直线距离公式,求解更简捷,这是将来上高中以后继续学习和掌握的方法(此处略),正如唐朝诗人王之涣说:“欲穷千里目,更上一层楼.” 面对阅卷中存在的问题和诸多空白卷,教师需要进行教学反思. (1)一次函数和二次函数的性质一直是中考命题的热点与重点,综合应用是学习的难点,解题的关键是熟练掌握二次函数和一次函数的性质,注意利用数形结合的思想进行解题.教师需要在立足教材基础上,对教材题不断地由浅入深进行改编和拓展,以不变应万变;需要在综合题、教学方法的改进上不断创新,有效地将学术形态的数学知识转化为教育形态的数学知识,进一步提升能力. (2)在教学中,教师应该在设计问题、组织内容和提问上下功夫,让学生亲身体会为什么要用分割法?分割有哪些方法?引导学生分析解题方法的优劣,让学生牢固掌握自己理解的方法.以三角形内接于抛物线的综合题比比皆是,解题教学重视转化的过程,培养学生观察发现、大胆分割、细心转化、精于计算、合作交流的精神,这符合创新意识和创新精神的培养,从根本上改变“注入式”“灌输式”教学. (3)教师要在转化能力、运算能力、逻辑推理能力上狠下功夫.通过观察课堂和学生的互动发现学生能根据基本数学活动经验进行解答,虽然在方法的选取上趋向一致(分割法),但运算上略有不足,所以教师在以后的教学中要精心设计教学过程,“授人以渔”,善于化整为零,各个击破,多把总问题分解成多个让学生能够垫垫脚摸得到、想得来的小问题,多渗透转化思想和数形结合的思想方法,以贴近学生认知为目标去启发,灵活运用所学知识提高学生的解题能力,进而促进学生核心素养的提升.
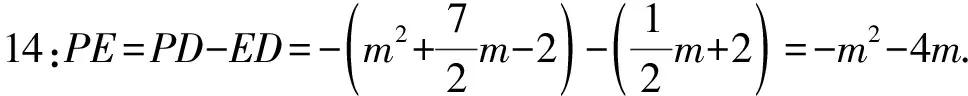


3 不同视角,发散思维

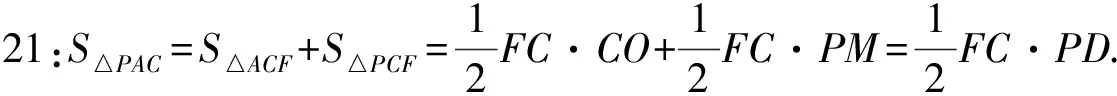

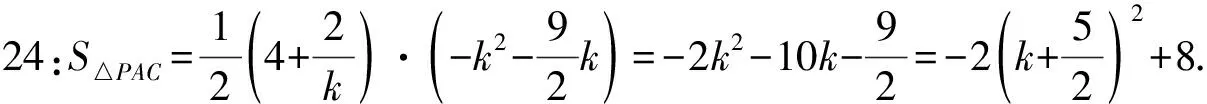
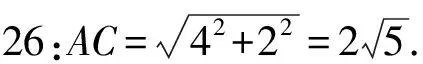

4 教学反思与建议
