引入眼动注视点的联合−交叉负载多模态认知诊断建模*

詹沛达

引入眼动注视点的联合−交叉负载多模态认知诊断建模*

詹沛达

(浙江师范大学教师教育学院心理学系; 浙江省智能教育技术与应用重点实验室, 金华 321004)

多模态数据为实现对认知结构的精准诊断及其他认知特征(如, 认知风格)的全面反馈提供了可能性。为实现对题目作答精度、作答时间(RT)和视觉注视点数(FC)的联合分析, 本文基于联合−交叉负载建模法提出3个多模态认知诊断模型。实证研究及模拟研究结果表明: (1)联合分析比分离分析更适用于多模态数据; (2)新模型可直接利用RT和FC中信息提高潜在能力或潜在属性的估计准确性; (3)新模型的参数估计返真性较好; (4)忽略交叉负载所导致的负面结果比冗余考虑交叉负载所导致的更严重。

认知诊断, 多模态数据, 题目作答时间, 注视点, 认知风格, 眼动

1 引言

个体的外显行为(如, 学习行为或问题解决行为)是由相互关联的多种认知过程及心理建构所共同决定的。因此, 在特定问题(任务)情境下, 对问题解决行为的合理分析不仅可以挖掘个体的认知结构, 还能反映个体的认知风格或认知流畅性等其他认知特征。认知风格是个体组织和处理信息的特征及相对稳定的方式, 反映了个体在感知、记忆、思维、判断和解决问题等方面的偏好或典型模式(Riding, 1997), 有助于调节认知加工过程的持续时间、强度、范围和速度(Gardner et al., 1959; Messick, 1989)。比如, 根据个体加工信息或解决问题的速度和精度, 可将个体分为沉思型或冲动型(Kagan, 1965);通常, 沉思型个体反应速度较慢但精度较高, 而冲动型个体反应速度较快但容易发生错误。再比如, 根据个体注意力的广度和专注度, 可将个体分为扫描者和聚焦者(Gardner et al., 1959)。在解决问题时, 扫描者的注意力广度宽但专注度低, 而聚焦者的注意力广度窄但专注度高。有研究表明在解决问题时扫描者的精度高于聚焦者的(Gardner et al., 1959; Holzman, 1966); 另有研究指出聚焦者对目标的注意力持续时间久于扫描者(Rimawi et al., 2020)。也有研究认为扫描和聚焦是两种可分离的风格(Messick, 1989), 根据扫描范围(即注意力广度)可将个体分为窄扫描者和宽扫描者, 根据聚焦程度(即专注度)可将个体分为聚焦者和非聚焦者; 而且, 两种风格还能相互组合。与具有相对稳定性的认知风格不同, 认知流畅性通常是指个体对信息处理或解决问题的难易程度的主观体验(Unkelbach, 2006), 流畅性可能会随所处理的信息、所解决的问题或所属的领域的不同而不同(Biancarosa & Shanley, 2015)。通常, 在有关流畅性测量的研究中, 流畅性被视为一种速度和精度的综合反映。已有研究表明达到流畅性水平的个体可以又快又好地解决问题(Wang & Chen, 2020)。总之, 为实现对个体学习现状的全面反馈, 对个体问题解决行为的分析应尝试从多视角切入, 不仅提供可反映认知结构的, 还要提供可反映认知风格或认知流畅性等其他认知特征的反馈信息。

近些年, 以促进个体学习为目的, 客观量化个体学习现状并提供诊断反馈的测评模式日益受到关注。其中, 认知诊断作为一种有代表性的诊断测评方式, 主要功能是诊断个体的学习现状(如, 知识掌握程度)并提供相应的反馈, 为促进个体学习提供了方法学支持(Ren et al., 2021; Tang & Zhan, 2021; 王立君等, 2020)。作为认知诊断的核心技术环节之一, 认知诊断模型(cognitive diagnosis model, CDM)或诊断分类模型的合理性影响着诊断结果的准确性、有效性和可解释性。CDM作为一种有约束的潜在类别模型, 描述了潜在属性和外显题目作答行为之间概率关系。通常, 潜在属性为类别变量(如, “0”表示“未掌握”, “1”表示“掌握”), 是根据个体完成复杂学习任务或解决复杂问题时所需具备的潜在技能或知识来确定的。目前, 针对不同的测验情境和理论假设, 已有许多CDM被提出(Rupp et al., 2010; von Davier & Lee, 2019), 比如常见的DINA模型(Junker & Sijtsma, 2001)及其一般化模型(de la Torre, 2011)。然而, 绝大多数CDM是基于题目作答精度(response accuracy, RA)这种单一且传统的数据源开发的(詹沛达, 2018), 导致它们所提供的诊断反馈范围有限: 仅关注对问题解决所需的认知技能或学科知识的诊断, 仅能提供可反映认知结构的反馈信息; 忽略问题解决时的信息加工速度和专注力(或视觉参与度)等其他相关建构, 难以提供可反映认知风格或认知流畅性等其他认知特征的反馈信息。换句话说, 目前绝大多数CDM提供的反馈信息有限, 不能全面反映个体间学习现状之间的差异, 进而可能限制有针对性干预的效果。导致这种局限性的可能原因之一是在传统的(基于纸笔测验的)认知诊断测评中很难采集到诸如题目作答时间(response time, RT)等数据。

近些年, 随着计算机(网络)化测验的普及, 对过程数据的采集已趋于常态化。过程数据是指由计算机记录的反映个体问题解决过程的含有时间戳的行为序列数据(Zhan & Qiao, 2022; Zoanetti, 2010;李美娟等, 2020; 刘耀辉等, 2022)。对过程数据的分析不仅可以挖掘个体的问题解决策略(Qiao & Jiao, 2018), 还可以探究个体的问题解决能力(Liu et al., 2018; Zhan & Qiao, 2022)。目前, RT数据作为一种有代表性的过程数据, 因为其具有标准化数据结构[1]标准化数据结构是指数据具有N × I的矩阵结构, 其中N表示被试总数, I表示题目总数。, 符合心理计量模型的建模与分析要求, 得到了研究者们的高度关注。已有研究表明, RT数据作为传统RA数据的补充, 不仅能够提供个体在问题解决过程中的加工速度信息, 还可以提高对潜在能力的估计精度(Bolsiova & Tijmstra, 2018; 詹沛达, 2019)和潜在属性的分类准确性(Zhan, Jiao, & Liao, 2018)。实际上, 计算机化测验的自动化特性使得它能够在个体解决问题过程中实时记录不限于过程数据的多种类型数据, 即多模态数据。多模态数据是指对于同一个描述对象, 通过多种仪器、测量设备或采集仪器获得到的互补的多样性数据(Lahat et al., 2015)。比如, 除结果数据(如, RA数据)和过程数据(如, RT数据)外, 通过嵌入式传感器或实验设备(如, 眼动仪), 计算机化测验还可以同步记录诸如眼动、身体运动及神经活动等生物计量数据。生物计量数据可用于提供有关个体与任务情境互动效果的反馈, 比如, 解决问题时个体的视觉参与度(Man & Harring, 2019; Zhan et al., 2022)或大脑激活水平(Jeon et al., 2021)。在技术增强测评环境中, 随着多模态数据采集技术的不断发展, 针对多模态数据的联合分析技术也应得到相应的关注和发展。

但是, 多模态数据的分析也给心理计量模型带来了挑战: 仅凭借单一的测量模型无法满足分析多模态数据的需求。因此, 在智能时代背景下, 基于技术增强测评环境, 建立心理与教育测量新范式, 探究多模态数据分析方法具有重要的理论意义和实践价值。对此, 遵循联合−层级建模法(van der Linden, 2007), Zhan等(2022)基于联合−层级认知诊断建模框架(Zhan, Jiao, & Liao, 2018)提出了联合−层级多模态认知诊断模型(joint-hierarchical multimodal CDM, H-MCDM); 首次在认知诊断领域实现对结果数据、过程数据和生物计量数据进行联合分析。其研究结果表明联合分析多模态数据不仅能为个体提供更全面的反馈还能提高诊断精度。然而, Ranger (2013)指出联合−层级建模的一个主要理论局限是仅当潜在变量之间的相关不等于0时, 各模态数据之间的信息才能相互被利用; 进而才有可能实现利用辅助数据所提供的信息提高对核心特质(如, 潜在能力)的估计精度(Bolsinova & Tijmstra, 2018)。对此, 有研究者提出联合−交叉负载建模法(Bolsinova & Tijmstra, 2018; Molenaar et al., 2015)。联合−交叉负载建模法可视为是对联合−层级建模法的拓广, 理论上可以通过交叉负载实现直接利用辅助数据(如, RT)为核心特质(如, 潜在能力)提供信息。鉴于H-MCDM是遵循联合−层级建模法构建的, 理论上也必然存在上述局限性; 这在一定程度上可能会影响该模型的实践应用性。对此, 本文聚焦于认知诊断领域, 针对结果数据、过程数据和生物计量数据, 拟基于联合−交叉负载建模法构建多模态认知诊断模型(joint-cross-loading MCDM, C-MCDM)。

首先, 简单回顾两种可联合分析多模态数据的联合建模法: 联合−层级建模法和联合−交叉负载建模法; 其次, 简单介绍视觉注视点数(visual fixation count, FC), 一个重要的眼动指标; 然后, 以传统的分离建模法为始, 分别介绍有关RA、RT和FC数据的测量模型, 继而引出H-MCDM; 接着, 阐述本研究新提出的3个C-MCDM, 基于实证研究将新模型与已有模型进行对比以展现新模型的现实可应用性及相对优势, 并通过两则模拟研究分别探究新模型的参数估计返真性和相对于H-MCDM的优势; 最后, 总结了研究结果并探讨了未来的研究方向。

2 多模态数据的联合分析

2.1 两种联合建模框架

目前, 联合−层级建模是使用最广泛的联合分析多模态数据的心理计量建模方法, 如图1(a)所示。如上文所述, RT数据作为一种有代表性的过程数据近些年受到高度关注, 研究者们提出了多个可联合分析RA和RT数据的联合−层级模型(de Boeck & Jeon, 2019; 郭磊等, 2017; 詹沛达, 2018)。在典型的联合−层级建模中, 第一层中构建RA数据和RT数据的测量模型: 潜在能力完全解释RA数据, 潜在加工速度完全解释RT数据; 而潜在能力和潜在加工速度之间的关系以二元正态分布的形式被建模在第二层结构模型中。尽管几乎所有的联合−层级模型都局限于分析RA和RT这两类数据, 但由于该建模思路具有较强的可扩展性, 基于该建模框架可以实现对更多类型数据的分析和对更多类型潜在建构的测量。比如, Jeon等(2021)通过联合分析RA数据和大脑激活这一生物计量数据, 测量了个体的潜在能力和大脑激活水平。Man和Harring (2020)通过联合分析RA数据、RT数据和FC数据, 测量了个体的潜在能力、潜在加工速度和视觉参与度。Bezirhan等(2021)联合分析了RA数据、RT数据和重访题目次数, 测量了个体的潜在能力、潜在加工速度和重访题目倾向。基于联合−层级建模, 在认知诊断领域, Zhan, Jiao和Liao (2018)首次将RT数据引入认知诊断建模中提出了联合−层级认知诊断建模框架, 如图1(b)所示; 该建模法同样具有可扩展性, 通过加入其他模态数据的测量模型, 实现多模态数据的联合分析(如, Zhan et al., 2022)。

与仅关注的RA数据的传统模型相比, Ranger (2013)指出联合−层级建模的主要理论局限是仅当潜在能力和潜在加工速度之间的相关系数不等于0时, 额外引入RT数据的联合−层级模型才能够提高对潜在能力参数的估计精度。Bolsinova和Tijmstra (2018)指出联合−层级建模未充分利用RT数据所提供的信息, 即假设RT数据仅受潜在加工速度的影响, 不受潜在能力的影响。然而, 在实际测验中, 可能存在潜在能力和潜在加工速度之间的相关系数较小(Bolsinova et al., 2017; Zhan, Liao, & Bian, 2018)以及不同能力的个体在解决问题时所花费的时间可能不同(Schaeffer et al., 1993)的情况。对此, 联合−交叉负载建模假设RT数据同时受个体的潜在能力和潜在加工速度的影响, 如图1(c)所示; 理论上, 无论潜在能力与潜在加工速度之间的相关系数多大, RT数据都可以直接为潜在能力参数的估计提供信息, 增加潜在能力参数的估计精度。但目前, 尚未有研究将该建模方法引入认知诊断领域, 这是本文要做的一项工作。

图1 多模态联合建模示意图(以作答精度和作答时间数据为例)

注: θ为潜在能力; τ为潜在加工速度; α为潜在属性;为题目作答精度;为题目作答时间;为题目数量;为属性数量; IRT为项目反应理论.

2.2 注视点数

在计算机化测验中, 通过嵌入式传感器可以记录个体解决问题时的生物计量数据; 其中, 眼动仪是被关注较多的一种, 已被用于大规模测评项目之中(Bos et al., 2005, 也见Rupp et al., 2010)。眼动指标可以提供有关个体在解决问题时的认知过程的证据。常见的眼动指标有注视点(提供眼睛看哪里信息)、眼跳(提供注视点位置发生变化的信息)、感兴趣区(提供注视点聚集区域的信息)和回视次数(提供个体将注视点返回到特定目标上的次数信息)等; 其中, 注视点是最常用的指标, 它可以反映个体对视觉目标区域的专注度(An et al., 2017), 或视觉目标区域对个体的重要性和吸引力(Poole et al., 2004)。聚焦在计算机化测验中, 作答题目时的注视点数(即FC数据)可以反映个体解决问题时的视觉参与度(Man & Harring, 2019; Zhan et al., 2022)。

2.3 多模态数据分析

本文以分析RA数据、RT数据和FC数据为例, 涉及3种可分析多模态数据的建模法: 分离建模法, 联合−层级建模法和联合−交叉负载建模法。

2.3.1 分离建模法

分离建模法延续传统心理计量学模型的做法, 对不同模态的数据分别建模、独立分析。为便于下文撰写, 将采用分离建模法分析多模态认知诊断数据的方法称为分离多模态认知诊断模型(separate MCDM, S-MCDM)。在S-MCDM中, 本文选用3个具有代表性的测量模型分别来分析RA数据、RT数据和FC数据。

首先, 选用高阶DINA (higher-order DINA, HO-DINA) (de la Torre & Douglas, 2004)模型作为RA数据的测量模型, 主要原因是为与基于联合−层级建模法的H-MCDM做对比。HO-DINA模型可描述为:

其次, 选用对数正态RT(lognormal RT, LRT)模型(van der Linden, 2006)作为RT数据的测量模型, 该模型可描述为:

式中,T为被试作答题目的时间(常以秒为单位); τ为被试的潜在加工速度, 表示被试投入到整个测验中的平均工作速度; ξ为题目的时间强度参数, 表示完成题目所必需的时间; ω为题目的时间精度参数。LRT模型假设当被试的潜在加工速度较高时则其RT较小。LRT模型也可简单记为:

最后, 为实现对个体视觉参与度的测量, Man和Harring (2019)提出了可分析FC数据的负二项注视点(negative binomial fixation, NBF)模型。NBF模型假设FC服从负二项分布, 并将FC解释为个体的视觉参与度与题目所需的必要注视点数量之间的权衡关系的产物。NBF模型描述了被试在作答题目时, 在贯序、独立的V次观察后成功提取了h次关键信息的概率分布, 即:

式中,V为被试解答题目时的FC; ε为被试的潜在视觉参与度, 可反映被试对问题情境中各种刺激的专注度;m为题目的视觉强度参数, 表示完成题目所必需的注视点数;h为题目上FC的离散程度参数。NBF模型也可简单记为:

2.3.2 联合−层级建模法

近年来, 人们越来越有兴趣去结合多模态数据所提供的信息对感兴趣的心理现象提供统一的解释。实际上, 在计算机化测验中, 对RA数据、RT数据和FC数据的采集几乎是同时进行的, 且它们提供的是被试在作答相同题目时的平行信息(如, 被试正确作答某题目耗时20秒并投入30个注视点), 因此, 也有研究者将这类多模态数据称之为平行数据(Jeon et al., 2021)。平行数据最大的优势在于它们包含有关同一个问题解决过程的平行信息, 如果这些信息可以被联合分析并相互利用, 不仅可以直接分析不同潜在变量之间的关系, 还有可能提高各自测量模型的参数估计准确性。

基于联合−层级认知诊断建模, Zhan等(2022)提出可同时分析RA数据、RT数据和FC数据的H-MCDM。如图2(a)所示, H-MCDM包含两层级模型: 测量模型和结构模型。在第一层测量模型中, 对3种模态数据分别建模, 这与S-MCDM类似, 不再赘述; 在第二层结构模型中, 通过三元正态分布来描述潜在能力、潜在加工速度和潜在视觉参与度三者之间的关系:

式中, μperson= (μθ, μτ, με)’为3个潜在变量的均值向量; Σperson为3个潜在变量的方差协方差矩阵。

2.3.3 联合−交叉负载建模法

如上文所述, 联合−层级建模的主要局限之一是: 理论上, 仅当潜在变量之间相关不为0时, 各模态数据之间的信息才能相互被利用。为了更直接地利用RT和FC这两个附属数据中的信息, 可使用联合−交叉负载建模法, 将潜在属性或潜在能力直接建模在RT测量模型和FC测量模型中。基于该逻辑, 本文提出3个C-MCDM, 如图2(b)～2(d)所示,分别为基于潜在能力的C-MCDM (C-MCDM-θ)、基于连接缩合规则的C-MCDM (C-MCDM-D)和基于补偿缩合规则的C-MCDM (C-MCDM-C)。3个模型遵循不同的逻辑假设, 其中, C-MCDM-θ假设被试的潜在能力的变化会影响其完成该题目的耗时及所用注视点数; 而C-MCDM-D和C-MCDM-C均假设被试的潜在属性掌握情况会影响其完成该题目的耗时和注视点数, 两者差异在于前者认为仅有被试掌握了题目所考查的所有属性后才会影响RT和FC, 而后者认为被试掌握该题目所考查的属性的数量会影响RT和FC (即掌握的越多影响越大)。另外, 为保证与S-MCDM和H-MCDM具有可比性, 本文设定在C-MCDM-D和C-MCDM-C中也存在高阶潜在结构, 但是否存在高阶潜在结构不影响建模。再有, 为了保证模型的可识别性(即θ和τ之间的以及θ和ε之间的相关性已经被交叉负载解释), 在3个C-MCDM中并没有使用三元正态分布来联接潜在能力、潜在加工速度和潜在视觉参与度这3个潜在变量(Bolsinova & Tijmstra, 2018; Molenaar et al., 2015)。小规模模拟研究结果显示在当前C-MCDM基础上再采用三元正太分布联接3个潜在变量后会导致参数估计不收敛, 尤其是三元正太分布中的方差和协方差。

图2 联合−层级和联合−交叉负载多模态认知诊断建模示意图

注: θ为潜在能力; τ为潜在加工速度; ε为潜在视觉参与度; α为潜在属性; Y为题目作答精度; T为题目作答时间; V为注视点数; I为题目数量; K为属性数量.

为便于表达, 用统一模型来表示3个C-MCDM。首先, 对RA数据而言仍选用HO-DINA模型作为其测量模型(见公式(1))。其次, 对RT数据和FC数据而言, 它们的测量模型可分别表示为:

式中, 函数(θ, α, q)表示对于考查给定属性的题目, 潜在能力或潜在属性如何影响其RT和FC:

φ和λ分别为函数(θ, α, q)对RT和FC的加权系数或交叉载荷; 以C-MCDM-D为例,φ和λ分别表示, 对于题目, 理想作答为1的被试和理想作答为0的被试之间(对数)RT和FC的均值的差异。鉴于已有研究表明潜在能力与潜在加工速度之间并不总是正相关(Zhan, Jiao, & Liao, 2018), 因此, 3个模型中并不限制φ和λ的正负号, 而由数据驱动决定。对于题目, 当φ> 0时, 一定程度反映了题目对被试作答时需付出的认知负荷的要求相对较低(如, 速度测验中的题目), 进而能力较高(或属性掌握越多)的被试会使用相对更少的时间来作答, 而能力较低的被试会使用相对更多的时间来作答; 而当φ< 0时, 一定程度反映了题目对被试作答时需付出的认知负荷的要求相对较高(如, 难度测验中的题目), 进而能力较高的被试会使用相对更多的时间来作答, 而能力较低的被试会使用相对更少的时间来作答(可能是动机较低导致的(Wise & Kong, 2005; Zhan, Jiao, & Liao, 2018))。同理, 对于题目, 当λ> 0时, 一定程度反映了题目所涉及的关键信息的数量较多, 进而能力较高的被试在作答该题目时会使用相对更多的注视点, 而能力较低的被试会使用相对较少的注视点(即难以提取到所有的关键信息); 而当λ< 0时, 一定程度反映了题目所涉及的关键信息的数量较少, 进而能力较高的被试在作答该题目时会使用相对更少的注视点, 而能力较低的被试会使用相对较多的注视点(可能是受到无关信息干扰, 难以确定关键信息的位置)。另外, 由于φ和λ是同一道题目的参数, 所以理论上有4种组合, 如表1所示; 当然, 表1中的描述只是一种可能性, 实践中还需要针对具体问题具体分析。

另外, 鉴于在认知诊断中提高潜在属性的诊断准确率才是关键, 3个C-MCDM均未考虑潜在加工速度和潜在视觉参与度对RA的影响, 即不考虑利用RA数据信息提高这两个潜在变量的参数估计准确性; 也没有考虑RT数据和FC数据之间信息的相互利用, 仍假设潜在加工速度和潜在视觉参与度之间存在相关。此时, 可以用二元正态分布描述潜在加工速度和潜在视觉参与度之间的关系:

2.3.4 认知结构诊断及认知特征推断

实际上, 相比于传统的仅分析RA数据的CDM而言, S-MCDM、H-MCDM和3个C-MCDM均能实现对多模态数据的分析, 研究者也均可以基于分析结果实现对个体认知结构的诊断及其他认知特征的推断。具体而言, 首先, 在MCDM中, 作为RA数据的测量模型, HO-DINA模型的主要功能就是诊断个体对潜在属性的掌握情况; 因此, 潜在属性模式的诊断结果可以较为直接地反映个体的认知结构。其次, 在MCDM中, 额外使用了LRT模型和NBF模型分别作为RT和FC数据的测量模型。与HO-DINA模型中将被试参数设为类别变量不同, LRT模型和NBF模型中的被试参数为连续变量; 因此, 无法像对潜在属性的诊断一样直接对个体的潜在加工速度和潜在视觉参与度进行分类, 进而无法直接实现对个体认知特征的分类。

表1 C-MCDM中φi和λi参数的正负取值可能反映的题目信息

注:φ和λ分别为函数(θ, α, q)对RT和FC的交叉载荷; θ为潜在能力; α为潜在属性;为题目所考查的属性; ↑为增加, ↓为下降; RT为题目作答时间; FC为注视点数.

表2 8种认知特征综合类别及可能的原因或行为表现(Zhan et al., 2022)

注: θ为潜在能力; τ为潜在加工速度; ε为潜在视觉参与度; +为大于均值; –为小于均值.

对此, 一种较为简单明了的方式是利用均值作为切点: 当个体的潜在能力大于均值时表明该个体属于认知能力(如, 问题解决能力)相对较高的一类, 反之则反; 当个体的潜在加工速度大于均值时表明该个体属于加工速度相对较快的一类, 反之则反; 当个体的潜在视觉参与度大于均值时表明该个体属于专注度较高的一类, 反之则反。理论上, 三者进一步组合, 可得到8种认知特征综合类别(Zhan et al., 2022); 表2呈现了这8种认知特征综合类别及可能的原因或行为表现。当然, 需要强调的是这种分类方式是比较粗糙的, 适用于对个体认知特征的粗略推断, 并非精确的测量或诊断结果。

2.4 贝叶斯参数估计

本文使用全贝叶斯马尔可夫链蒙特卡洛算法对S-MCDM、H-MCDM和3个C-MCDM进行参数估计, 并基于JAGS (Plummer, 2015)实现。网络版附录S1章节中呈现了模型参数估计对高、中和低信息先验分布的鲁棒性分析结果, 结果表明新模型对包含不同信息量的先验分布具有一定的鲁棒性。结合已有实证数据分析经验和已有研究结果(Man & Harring, 2019; Zhan et al., 2022), 正文所有参数估计均采用中信息先验分布。示例数据及相应的JAGS代码已分享在网络版附录中, 关于如何使用JAGS进行贝叶斯参数估计可参见Zhan等(2019)。

3 实证数据分析

鉴于本文所提出模型中包含φ和λ两个新参数, 暂缺乏对它们的取值范围的了解, 难以进行恰当的模拟研究(即, 不知根据何种分布来生成它们的真值); 因此需要先进行实证研究, 以展现新模型的实践可应用性, 并为模拟研究中参数真值生成提供参考依据。

3.1 数据描述和分析

为对比3种多模态数据分析方法(即5个MCDM)的表现, 我们选用来自一项技术增强测评环境下的数学测验的数据。该数据[2]需要强调的是由于该数据中涉及到某高利害测验中敏感信息(例如, 题目), 所以该数据并不对外公开。但研究者可以尝试向Man和Harring (2019)或Zhan等(2022)的通讯作者以合理的理由索取。在美国东海岸一所大学的眼动实验室采集的(Man & Harring, 2019), 其中包括= 93名(矫正)视力正常的大个体对= 10道题目的作答。该测验考查= 4个潜在属性: (α1)算数(arithmetic)、(α2)代数(algebra)、(α3)几何(geometry)和(α4)数据分析(data analysis), 测验Q矩阵见图3。该数据包含3种同时采集的数据: 结果数据(即RA)、过程数据(即RT)和生物计量数据(即FC)。另外, 有关该数据更详细的描述请参阅Man和Harring (2019)。注意, Man和Harring (2019)使用的是语言推理数据, 而Zhan等(2022)及本文使用的是同一批次采集的数学测验数据。

分别使用S-MCDM、H-MCDM和3个C-MCDM分析该数据。5个模型均使用两条马尔可夫链(随机起点), 每条链包含60, 000次迭代(预热40, 000次), 稀疏值1; 最终剩余40, 000次迭代用于计算后验均值和后验标准差。使用潜在量尺缩减因子(PSRF) < 1.2 (Brooks & Gelman, 1998)作为参数估计收敛检验标准(Brooks & Gelman, 1998; de la Torre & Douglas, 2004)。使用后验预测模型检验(posterior predictive model checking) (PPMC; Gelman et al., 2014)来评估模型−数据绝对拟合, 其中后验预测概率(posterior predictive probability,)接近0.5表示模型与数据拟合(通常,< 0.05或> 0.95可被视为不拟合(Gelman et al., 2014))。在PPMC中使用测验统计量(test statistics) (即仅关注真实数据与预测数据之间的差异, 不涉及具体模型参数) (Levy & Mislevy, 2016)。由于目前缺乏针对联合模型的绝对拟合评价指标, 在3个模型中, 我们均分别评估不同模态数据与其测量模型之间的拟合关系。此外, 使用DIC作为模型−数据的相对拟合指标用于模型选择; 指标值越小表示模型与数据拟合的越好。

图3 实证数据Q矩阵; 白色表示“0”, 灰色表示“1”

3.2 结果

表3 实证数据中模型−数据拟合指标

注: –2LL = –2 log likelihood; DIC = deviance information criterion;= 后验预测概率; RA = 作答精度; RT = 作答时间; FC = 注视点数。

通过观察H-MCDM中潜在能力与潜在加工速度的估计值之间的相关系数(–0.008, SE = 0.278)和潜在能力与潜在视觉参与度的估计值之间的相关系数(0.004, SE = 0.252), 可发现两相关系数均接近于0, 理论上难以发挥H-MCDM相较于S-MCDM的优势; 反观, 由于C-MCDM-θ可以直接利用RT和FC数据中的信息来降低对潜在能力参数的估计标准误(见图4), 所以导致该模型对数据的拟合相对更好。下文将基于C-MCDM-θ模型的分析结果进行阐述。

表4呈现了C-MCDM-θ模型中3个测量模型的参数估计值及φ和λ的估计值。首先, 对测量模型中参数而言, 该结果与Zhan等(2022)的估计结果基本一致。其中, 前两题的猜测参数较大, 而第6题的失误参数较大。各题目的时间强度参数的平均值约为3.33, 表明被试完成这些题目所必须的平均耗时约为28秒(接近该数据中RT的均值33.99)。各题目的视觉强度参数的平均值约为4.68, 表明被试完成这些题目所必须的注视点数约为107个(接近该数据中FC的均值114.53)。其次, 对φ和λ而言, 一个显著特点是对于同一道题目两参数的正负号相反。结合表1中的描述, 表明该测验中题目所包含的关键信息数量与认知负荷要求相匹配, 即关键信息多则认知负荷要求高, 反之则反。进一步, 图5呈现φ和λ的估计值分布。发现φ估计值的中位数 < 0, 一定程度反映该测验中多数题目的认知负荷要求相对较高, 进而个体的潜在能力越高则其解题时所消耗的时间越长; 另外, 发现λ估计值的中位数 > 0, 一定程度反映该测验中多数题目所包含的关键信息数量较多, 进而个体的潜在能力越高则其解题时所呈现的注视点数越多。

表4 实证数据中C-MCDM-θ模型的题目参数估计值

注: g = 猜测参数; s = 失误参数; ξ = 时间强度参数; ω = 时间精度参数;= 视觉强度参数;= 视觉区分度参数; 括号内为标准误(后验标准差)。

表5呈现了基于C-MCDM-θ模型的反馈样例, 包括对认知结构和其他认知特征的反馈信息, 以展现联合分析多模态数据的优势。以被试5、9和65为例, 3人在潜在属性上的诊断结果相同, 但他/她们在潜在能力、潜在加工速度和潜在视觉参与度上的估计值有较大差异; 这表明即便他/她们具有相同的认知结构, 他/她们在认知风格或认知流畅性等认知特征方面也可能不同。另外, 对于认知结构有缺失的被试, 若实施有针对性干预, 除缺失的潜在属性外, 还应考虑不同个体的认知特征, 采取更恰当的干预措施。比如, 被试34和67均缺失属性2和4, 但由于两者的认知特征不同, 或许可以尝试不同的有针对性干预措施。对于被试34 (冲动型+非聚焦者)而言, 由于其倾向于仅根据从问题情境中提取的部分信息就仓促做出决定, 除缺失的潜在属性外, 还可以尝试培养该被试的视觉参与度, 并鼓励其认真审题、谨慎作答。而被试67 (认知不流畅+聚焦者)似乎有解决问题的动机或欲望但由于能力有限即便视觉参与度较高也无法提取题目中的关键信息; 所以对该被试而言, 应该着重补救其所缺失的潜在属性。

表5 实证数据中个体认知结构诊断及其他认知特征推断样例

注: θ = 潜在能力; τ = 潜在加工速度; ε = 潜在视觉参与度; 括号内为标准误(后验标准差)。

4 模拟研究

上文已经通过实证研究展示了新模型的实用性及相对优势。本节通过两则模拟研究进一步探究新模型的心理计量学性能。其中, 研究1拟在多种模拟测验条件下探究新模型的参数估计返真性; 研究2拟对比新模型和H-MCDM的相对表现, 以展现新模型的相对优势及考虑交叉负载的必要性。

4.1 模拟研究1

4.1.1 数据生成与分析

模拟研究中, 设定3个操纵变量: (1)样本量: 100和500, 考虑到CDM的实际应用场景及眼动研究目前可能的被试数量, 本研究主要关注新模型在小样本条件下的表现; (2)测验长度: 15和30, 固定潜在属性数量= 5, Q矩阵见图6 (该Q矩阵满足DINA模型的参数可识别性要求(Gu & Xu, 2021)); (3)交叉载荷: λ= –φ= 0、0.2和0.5, 其中, 0.2和0.5的设定参考实证数据分析结果(见表4), 而设置0的目的是为了探究当不存在交叉负载时新模型的表现。

被试的潜在能力、潜在加工速度和潜在视觉参与度按如下方法生成:

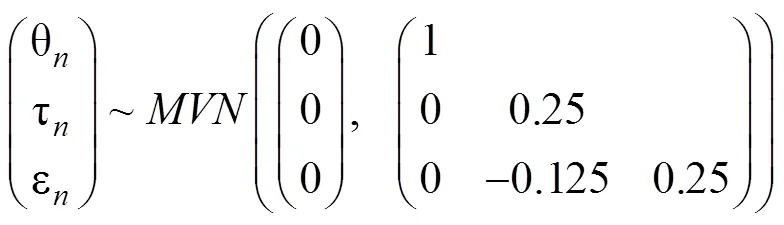
该设定中ρτε= –0.5参考了上文实证研究结果及Zhan, Jiao和Liao (2018)和Man和Harring (2019)的设定: 假设个体的加工速度越慢则视觉参与度越高(即沉思型多匹配聚焦者); 同时, 个体学习的加工速度越快则视觉参与度越低(即冲动型多匹配非聚焦者); 另外, 遵循图2(b)～2(d)中的设定, 设定ρθτ= 0和ρθε= 0, 原因是在交叉负载认知诊断建模法中θ与τ之间的关系及θ与ε之间的关系已经由交叉载荷来描述。

另外, 参考上文实证研究结果及Zhan, Jiao和Liao (2018)、Man和Harring (2019)的设定, 题目参数按如下方法生成

ω～(1.25, 2)和h～InvGamma (2, 6)。另外, 属性区分度参数被固定为γ1k= 1.5, 属性难度参数被固定为γ0= (–1.5, –0.5, 0, 0.5, 1.5)’, 并依据公式2生成被试的属性模式。

最后, 在6种(2样本量 × 2测验长度 × 2交叉载荷)模拟测验条件下, 分别依据C-MCDM-θ、C-MCDM-D和C-MCDM-C各生成30组平行数据(RA数据、RT数据和FC数据)。

4.1.2 结果

在所有模拟测验条件下, 3个分析模型中的所有参数的PSRF值均满足PSRF < 1.2的收敛标准(且98%以上的参数满足相对更严苛的PSRF < 1.1收敛标准(Brooks & Gelman, 1998))。

图7分别呈现了3个模型的属性(模式)判准率。首先, 当交叉载荷为0时, 3个模型在不同测验条件的表现基本一致。其次, 随着交叉载荷的提高, 可发现3个模型的ACCR和PCCR在不同测验条件下均有所提升, 其中C-MCDM-C提升幅度最大, C-MCDM-D次之, C-MCDM-θ最小。这表明, 在联合−交叉负载建模法中, 为提高诊断分类准确性, 直接利用RT和FC数据为被试对属性的掌握情况提供辅助信息比先为高阶潜在能力提供辅助信息再间接影响被试对属性的掌握更有效。对此, 一种可能的原因是, 在C-MCDM-θ中, HO-DINA模型(RA数据的测量模型)中的高阶潜在能力作为一种辅助参数其参数估计返真性通常较差(de la Torre & Douglas, 2004; Zhan, 2020; Zhan et al., 2020); 因此, 尽管利用RT和FC数据中的辅助信息可以适当提高高阶潜在能力的参数估计准确性, 但或许是提升幅度有限, 难以有效促进潜在属性的估计准确性。这点在图4中也可以得到印证。

图8分别呈现了3个模型的潜在能力、潜在加工速度和潜在视觉参与度的参数估计返真性。首先, 3个模型在所有条件的参数估计偏差都接近于0。其次, 对C-MCDM-θ而言, 随着交叉载荷的提高, 潜在能力的RMSE逐渐下降且Cor逐渐提高, 表明随着RT和FC数据中的辅助信息的提高, 潜在能力的估计返真性会随之增加; 但值得注意的是, 随着交叉载荷的提高, 尽管潜在能力的估计返真性有所提升, 但潜在加工速度和潜在视觉参与度的估计返真性却出现下降现象。然后, 对C-MCDM-D和C-MCDM-C而言, 由于RT和FC数据并未直接为潜在能力提供辅助信息系; 因此, 随着交叉载荷的提高, 两模型中潜在能力的RMSE略微下降且Cor略微提高。

由于篇幅限制, 3个模型的题目参数估计返真性呈现在网络版附录表S2-S4中。整体而言, 在不同测验条件下, 3个模型的题目参数估计返真性都较好, 呈现出较为一致的趋势: 被试数量增加有助于提高题目参数估计返真性, 而测验长度和交叉载荷大小的影响似乎很小。

注: N = 样本量; I = 测验长度; CL = 交叉载荷; ACCR = 属性判准率; PCCR = 属性模式判准率.

图8 模拟研究1中3个C-MCDM的潜在能力、潜在加工速度和潜在视觉参与度的参数估计返真性.

注: N = 样本量; I = 测验长度; CL = 交叉载荷; θ = 高阶潜在能力; τ = 潜在加工速度; ε = 潜在视觉参与度; Bias = 偏差; RMSE = 均方根误差; Cor = 估计值与真值的相关系数.

4.2 模拟研究2

4.2.1 数据生成与分析

为进一步探究新模型的相对优势及交叉−负载的必要性, 模拟研究2中分别使用3个新模型和H-MCDM作为数据生成模型, 然后对比探究几个模型的表现。当3个新模型作为数据生成模型时, 被试的潜在能力、潜在加工速度和潜在视觉参与度的生成方法与模拟研究1保持一致(公式12); 交叉载荷(λ= –φ)从均值为0.1、标准差为0.3的正态分布中抽取, 表明交叉载荷在题目之间存在差异(该设定参考了上文实证数据的结果)。当H-MCDM作为数据生成模型时, 被试的潜在能力、潜在加工速度和潜在视觉参与度按如下分布生成:

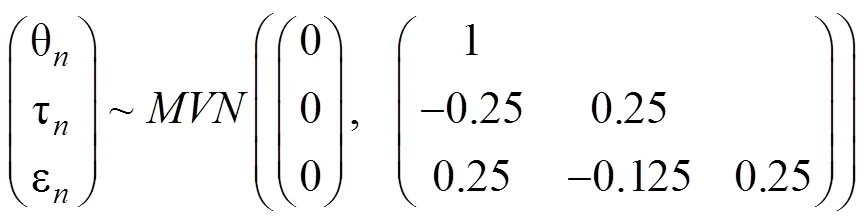
此时, ρθτ= –0.5、ρθε= 0.5和ρτε= –0.5, 该设定参考了已有实证数据的结果(Zhan, Jiao, & Liao, 2018; Man & Harring, 2019): 假设学生能力越高则加工速度越慢且视觉参与度水平越高; 同时, 学生学习能力越低则加工速度越快且视觉参与度水平越低。另外, 每种模拟条件下均固定被试量= 500和测验长度= 30, 其他设定均与模拟研究1保持一致。每种模拟条件下生成30组数据。

当3个新模型作为数据生成模型时, 仅使用数据生成模型和H-MCDM分析数据; 当H-MCDM作为数据生成模型时, 使用H-MCDM和3个新模型分析数据。参数估计设定(如, 链数和链长等)、收敛指标和返真性指标等均与模拟研究1保持一致。

4.2.2 结果

表6呈现不同条件下各数据分析模型与数据的拟合情况。首先, 无论何种条件下, 数据生成模型本身对模拟数据的拟合均相对更好。其次, 根据DIC可发现, 当C-MCDM作为数据生成模型时, C- MCDM较H-MCDM的相对优势较大; 而当H-MCDM作为数据生成模式时, H-MCDM较C-MCDM的相对劣势较小; 表明C-MCDM对不同测验条件的兼容性比H-MCDM更好。即忽略可能存在的交叉负载所导致的模型−数据不拟合比冗余考虑存在交叉负载所导致的模型−数据不拟合的程度更大。表7呈现了不同条件下各数据分析模型的属性判准率。结果的整体趋势与DIC的类似, 即忽略可能存在的交叉负载对PCCR的负面影响比冗余考虑存在交叉负载对PCCR的负面影响更大。另外, 潜变量的和题目参数的返真性也均呈现类似的趋势(见网络版附录表S5-S6)。总之, 模拟研究2结果表明忽略可能存在的交叉负载所导致的负面结果比冗余考虑存在交叉负载所导致的更严重, 即C-MCDM对测验情境的兼容性优于H-MCDM的。

表6 模拟研究2中模型−数据拟合情况

表7 模拟研究2中潜在属性(模式)判准率.

5 总结与展望

5.1 总结

个体的问题解决行为是彼此相关的多种认知过程及心理建构所共同决定的。在技术增强测评环境中, 通过多种仪器或测量设备采集的多模态数据为实现对个体认知结构的精准诊断及其他认知特征的全面反馈提供了可能性。本文以对RA数据、RT数据和FC数据的分析为例, 基于联合−交叉负载建模法提出了3个具有不同理论假设的C-MCDM。其中, C-MCDM-θ假设被试的潜在能力的变化会影响其完成该题目的耗时和所用注视点数; 而C- MCDM-D和C-MCDM-C均假设被试的潜在属性掌握情况会影响其完成该题目的耗时和所用注视点数, 两者差异在于前者认为仅有被试掌握了题目所考查的所有属性后才会影响RT和FC, 而后者认为被试掌握该题目所考查的属性的数量会影响RT和FC。然后, 本文以一则实证数据为例对比探究了5个MCDM的表现, 包括基于传统分离建模法的S-MCDM、基于联合−层级建模法的H-MCDM和新提出的3个C-MCDM。实证研究结果表明(1)联合分析(即H-MCDM和C-MCDM)比分离分析(即S- MCDM)更适用于提供平行信息的多模态数据; 且(2)从模型−数据拟合角度看, 新模型比H-MCDM更拟合该数据。此外, 实证研究也向读者展示了如何根据数据分析结果来实现对个体认知结构的诊断及其他认知特征(如, 认知风格)的推断。最后, 使用两则模拟研究进一步探讨新模型的表现。模拟研究1作为对实证研究的补充, 探究了3个新模型在不同模拟测验条件的参数估计返真性。模拟研究2对比探讨了3个新模型和H-MCDM的表现, 以展示新模型的相对优势及考虑交叉负载的必要性。模拟研究1结果表明(1)全贝叶斯MCMC算法能够为3个新模型提供较好的参数估计返真性, 且3个新模型中各参数估计均可有效收敛; (2)实践应用中, 充足的题目数量是保证被试参数估计准确性的必要条件之一; (3)在不以题库建设为目标的(或其他题目参数相对不重要的)应用场景中, 100人的小样本量足以满足提供较为精准的被试参数估计值。模拟研究2结果表明忽略可能存在的交叉负载所导致的负面结果比冗余考虑存在交叉负载所导致的更严重, 即C-MCDM对测验情境的兼容性优于H- MCDM的。总之, 本文通过实证研究阐明了新模型的现实可应用性, 并通过模拟研究阐明了新模型具有良好的心理计量学性能。

综上所述, 对本文的理论创新、理论贡献和应用价值做如下总结:

(1)理论创新: 首次将联合−交叉负载建模法引入认知诊断领域, 提出3种不同假设的C-MCDM;

(2)理论贡献: 填补了在认知诊断领域缺少联合−交叉负载模型的空白;

(3)应用价值: 从全面反馈视角出发, 以认知风格和认知流畅性为例, 尝试在认知诊断中提供认知结构以外其他认知特征的反馈; 丰富了认知诊断反馈的范围, 增加了认知诊断的实践价值。

另外, 本文遵循Zhan等(2022)的做法, 将实验心理学与心理与教育测量相结合, 尝试将眼动数据引入心理计量模型; 这在一定程度上拓展了心理与教育测量的研究范式, 为今后进一步将实验心理学基于仪器的测量或量化研究方法引入传统心理与教育测量中提供了新视角。

值得强调的是由于新提出的3个C-MCDM与H-MCDM是基于不同联合建模方法构建的, 即它们基于不同的理论假设。在本文中, 尽管3个C-MCDM对实证数据的拟合程度优于H-MCDM, 这并不代表它们三者在任何测验情境下都优于H-MCDM; 比如, H-MCDM的相对优势是理论结构简单、待估计参数数量较少。因此, 本文更多的是在认知诊断领域向读者提供一种基于联合−交叉负载建模法的多模态数据分析视角和方法, 以期进一步丰富多模态诊断数据分析模型的可选项。我们建议后续使用者针对特定的实证数据, 同时使用多个MCDM对数据进行联合分析, 并基于数据−模型拟合指标来选择相对最合适的模型, 并结合模型的构建理论对分析结果做进一步解读。

5.2 局限与展望

本文仍有一些局限性, 值得后续做进一步探究。第一, 与已有联合分析RA数据和RT数据的研究相比, 尽管本文仅额外分析了一种眼动数据——注视点数(FC), 但鉴于联合−层级建模法和联合−交叉负载建模法的灵活扩展性, 其他类型的眼动数据或其他模态数据(如, 脑电[Jeon et al., 2021])也可尝试被纳入分析中, 进而提出更全面的可联合分析更多模态数据的认知诊断模型。

第二, 本文以3个代表性的测量模型(即HO- DINA模型、LRT模型和NBF模型)为例阐述了联合−交叉负载认知诊断模型的构建。同样, 鉴于联合−交叉负载建模法的灵活扩展性, 后续针对不同的测验情境可分别替换不同的测量模型。当然, 需要强调的是测量模型的更换并不影响本文的主要创新点——联合−交叉负载认知诊断建模法。

第三, 遵循Zhan等(2022), 利用多模态诊断数据本文只关注到对有限认知特征的推断, 如沉思型−冲动型认知风格、聚焦者认知风格和认知流畅性。实际上, 个体的认知特征还有很多, 仅认知风格就还有其他的分类方式, 比如场独立性−场依存性、言语型−视觉型等; 从全面反馈的视角看, 未来是否有可能利用多模态的数据实现对更多认知特征的推断, 甚至对是一些非认知因素(如, 动机、情绪和信念)的识别, 是非常值得关注的研究方向。

第四, 本文主要是提供了一种多模态诊断数据的分析方法, 实际上, 对多模态数据的利用可以延伸到很多已有模型中。比如, 后续研究可以将多模态数据引入多策略CDM (Ma & Guo, 2019)、多水平CDM (Wang & Qiu, 2019)和多级评分CDM (Ma & de la Torre, 2016)中, 甚至考虑将多模态数据引入到一些非参数诊断法中(如, 聚类分析)等。

第五, 本文提出的3个C-MCDM均未考虑潜在加工速度和潜在视觉参与度对RA的影响, 即未考虑利用RA数据信息提高这两个潜在变量的参数估计精度。后续, 若有必要也可尝试C-MCDM做进一步拓广, 纳入上述未考虑的路径(郑天鹏等, in press), 开发全交叉负载模型; 只不过要额外注意模型可识别性问题。

第六, 如2.3.4节中所述, 由于在RT和FC测量模型中的被试参数为连续变量, 无法像对潜在属性的诊断一样直接对个体的潜在加工速度和潜在视觉参与度进行分类, 进而无法直接实现对个体认知特征的分类。对此, 本文采用了以均值为切点的分类方法, 并依据潜在能力、潜在加工速度和潜在视觉参与度的分类组合, 尝试对个体认知特征的推断。需要强调的是(1)这种分类方法是比较粗糙的, 适用于对个体认知特征的粗略推断, 并非精确的测量或诊断结果; (2)这种分类方法所利用的信息尚有限, 仅利用了潜在能力、潜在加工速度和潜在视觉参与度这3个潜在变量的估计值作分类依据。未来, 为实现对个体认知特征的更精准推断甚至是测量, 可尝试从3个角度突破: (1)综合利用更多模态的数据来实现对个体认知特征的推断, 以期为推断性分类提供更多的参考信息; (2)尝试借鉴计算机化分类测验中对连续变量的分类方法(Ferguson, 1969), 以期改进以均值为切点的分类方法; (2)直接通过类别变量构建特定认知特征的被试参数(Wang & Chen, 2020), 以期实现对个体认知特征的测量而非推断。

第七, 由于现实硬件条件的限制(如, 没有大批量眼动仪), 本文所分析的实证数据仍属于小规模测验(由于成本仪器成本原因, 在未来一段时间, 涉及实验仪器采集数据的研究都会受限于被试量的问题)。尽管模拟研究结果显示, 在不考虑建立题库的应用场景下小样本量(100人)也可以满足要求, 但在大规模测验和涉及题库的应用场景(如, 计算机化自适应测验)中, 这些硬件条件的限制都会制约多模态数据分析方法的实际应用。随着测量方式及数据分析技术的不断发展, 充分利用计算机(网络)技术, 尤其是人工智能的介入, 并结合便携式和低成本的心理学实验仪器, 我们期待也有理由相信未来可以突破硬件条件的限制, 在大规模测验中实现对多模态数据的采集与分析。

最后, 在贝叶斯参数估计值中, 先验分布的选择反映了数据分析者对模型参数的信念或已有经验。根据已有数据分析经验以及已有研究结果(Man & Harring, 2019; Zhan et al., 2022), 本文选取了特定的先验分布。尽管鲁棒性分析表明模型的参数估计结果受包含不同信息量的先验分布的影响较小, 但这并不意味着本文所用的先验分布适用于所有测验情境。在后续的实践应用中, 针对全新的实证数据, 数据分析者也可尝试使用超先验分布来探索恰当的先验分布。

An, L., Wang, Y., & Sun, Y. (2017). Reading words or pictures: Eye movement patterns in adults and children differ by age group and receptive language ability.791. https://doi.org/10.3389/fpsyg.2017.00791

Bezirhan, U., von Davier, M., & Grabovsky, I. (2021). Modelingitem revisit behavior: The hierarchical speed-accuracy-revisitsmodel.(2), 363−387.

Biancarosa, G., & Shanley, L. (2015). What is fluency? In K. D. Cummings & Y. Petscher (Eds.),(pp. 1−18). Springer.

Bolsinova, M., de Boeck, P., & Tijmstra, J. (2017). Modelling conditional dependence between response time and accuracy., 112−1148. https://doi.org/10.1007/ s11336-016-9537-6

Bolsinova, M., & Tijmstra, J. (2018). Improving precision of ability estimation: Getting more from response times.(1), 13−38.

Bos, W., Lankes, E.-M., Prenzel, M., Schwippert, K., Valtin, R., & Walther, G. (Eds). (2005).[IGLU: Supplementary in-depth analyses of reading comprehension, context effects, and additional studies]. Münster: Waxmann.

Brooks, S. P., & Gelman, A. (1998). General methods for monitoring convergence of iterative simulations.(4), 434–455. https://doi.org/10.2307/1390675

de Boeck, P., & Jeon, M. (2019). An overview of models for response times and processes in cognitive tests.102.

De la Torre, J. (2011). The generalized DINA model framework., 179–199.

De la Torre, J., & Douglas, J. A. (2004). Higher-order latent trait models for cognitive diagnosis.(3), 333–353. https://doi.org/10.1007/BF02295640

Gardner, R. W., Holzman, P. S., Klein, G. S., Linton, H. B., & Spence, D. (1959). Cognitive control: A study of individual consistencies in cognitive behavior., Monograph 4.

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., & Rubin, D. B. (2014).. Boca Raton: CRC Press.

Gu, Y., & Xu, G. (2021). Sufficient and necessary conditions for the identifiability of the Q-matrix., 449−472.

Guo, L. Shang, P., & Xia, L. (2017). Advantages and illustrations of application of response time model in psychological and educational testing.(4), 701–712.

[郭磊, 尚鹏丽, 夏凌翔. (2017). 心理与教育测验中反应时模型应用的优势与举例.(4), 701–712.]

Holzman, P. S. (1966). Scanning: A principle of reality contact., 835−844.

Jeon, M., de Boeck, P., Luo, J., Li, X., & Lu, Z.-L. (2021). Modeling within-item dependencies in parallel data on test responses and brain activation.(1), 239− 271. https://doi.org/10.1007/s11336-020-09741-2

Junker, B. W., & Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory.(3), 258–272.

Kagan, J. (1965). Reflection-impulsivity and reading ability in primary grade children.(3), 609–628.

Lahat, D., Adali, T., & Jutten, C. (2015). Multimodal data fusion: An overview of methods, challenges, and prospects.(9), 1449−1477.

Levy, R., & Mislevy, R. J. (2016).. Boca Raton, FL: CRC Press.

Li, M., Liu, Y., & Liu, H. (2020). Analysis of the problem- solving strategies in computer-based dynamic assessment: The extension and application of multilevel mixture IRT model.(4), 528−540.

[李美娟, 刘玥, 刘红云. (2020). 计算机动态测验中问题解决过程策略的分析: 多水平混合IRT模型的拓展与应用.(4), 528−540.]

Liu, H., Liu Y., & Li, M. (2018). Analysis of process data of PISA 2012 computer-based problem solving: Application of the modified multilevel mixture IRT model., 1372.

Liu, Y., Xu, H., Chen, Q., & Zhan, P. (2022). The measurement of problem-solving competence using process data.(3), 522−525.

[刘耀辉, 徐慧颖, 陈琦鹏, 詹沛达. (2022). 基于过程数据的问题解决能力测量及数据分析方法.(3), 522−525.]

Ma, W., & de la Torre, J. (2016). A sequential cognitive diagnosis model for polytomous responses.(3), 253–275.

Ma, W., & Guo, W. (2019). Cognitive diagnosis models for multiple strategies.(2), 370−392.

Man, K., & Harring, J. R. (2019). Negative binomial models for visual fixation counts on test items.(4), 617−635. http://doi. Org/0.1177/0013164418824148

Man, K., & Harring, J. R. (2020). Assessing preknowledge cheating via innovative measures: A multiple-group analysis of jointly modeling item responses, response times, and visual fixation counts.,(3), 441–465. https://doi.org/10.1177/ 0013164420968630

Messick, S. (1989). Cognitive style and personality: Scanning and orientation toward affect.s, RR-89-16. https://doi.org/10.1002/j.2330-8516.1989.tb00 342.x

Molenaar, D., Tuerlinckx, F., & van der Maas, H. L. (2015). A bivariate generalized linear item response theory modeling Framework to the Analysis of Responses and Response Times.,(1), 56–74.

Plummer, M. (2015).. Retrieved from http://mcmc-jags.sourceforge.net/

Poole, A., Ball, L. J., & Phillips, P. (2004). In search of salience: A response-time and eye-movement analysis of bookmark recognition. In S. Fincher, P. Markopoulos, D. Moore, & R. Ruddle (Eds.),(pp. 363–378). London, England: Springer.

Ranger, J. (2013). A note on the hierarchical model for responses and response times in tests of van der Linden (2007).(3), 538−544.

Ren, H., Xu, N., Lin, Y., Zhang, S., & Yang, T. (2021). Remedial teaching and learning from a cognitive diagnostic model perspective: Taking the data distribution characteristics as an example., 628607. https:// doi.org/10.3389/fpsyg.2021.628607

Riding, R. J. (1997). On the nature of cognitive style.(1-2), 29−49.

Rimawi, O., Al-Halabiyah, F., & Hussein, O. (2020). The cognitive style (focusing-scanning) among Al-Quds University students.(1), 143−154.

Rupp, A. A., Templin, J. L., & Henson, R. (2010).. New York: Guilford Press.

Schaeffer, G. A., Reese, C. M., Steffen, M., McKinley, R. L., & Mills, C. N. (1993).. Princeton, NJ: Educational Testing Service.

Tang, F., & Zhan, P. (2021). Does diagnostic feedback promote learning? Evidence from a longitudinal cognitive diagnostic assessment.,. https://doi.org/10.1177/ 23328584211060804

Unkelbach, C. (2006). The learned interpretation of cognitive fluency.(4), 339−345.

Van der Linden, W. J. (2006). A lognormal model for response times on test items.(2), 181−204.

Van der Linden, W. J. (2007). A hierarchical framework for modeling speed and accuracy on test items.(3), 287−308.

Von Davier, M., & Lee, Y.-S. (2019).. New York, NY: Springer.

Wang, L., Tang, F., & Zhan, P. (2020). Effect analysis of individualized remedial teaching based on cognitive diagnostic assessment: Taking “linear equation with one unknown” as an example.(6), 1490−1497.

[王立君, 唐芳, 詹沛达. (2020). 基于认知诊断测评的个性化补救教学效果分析: 以“一元一次方程”为例.(6), 1490−1497.]

Wang, S., & Chen, Y. (2020). Using response times and response accuracy to measure fluency within cognitive diagnosis models.(2), 600–629.

Wang, W. C., & Qiu, X. L. (2019). Multilevel modeling of cognitive diagnostic assessment: The multilevel DINA example.(1), 34−50.

Wise, S. L., & Kong, X. (2005). Response time effort: A new measure of examinee motivation in computer-based tests.(2), 163–183

Zhan, P. (2018).(Unpublished doctoral dissertation). Beijing Normal University.

[詹沛达. (2018).(博士学位论文). 北京师范大学.]

Zhan, P. (2019). Joint modeling for response times and response accuracy in computer-based multidimensional assessments.(1), 170–178.

[詹沛达. (2019). 计算机化多维测验中作答时间和作答精度数据的联合分析.(1), 170–178.]

Zhan, P. (2020). A Markov estimation strategy for longitudinal learning diagnosis: Providing timely diagnostic feedback.(6), 1145− 1167. https://doi.org/10.1177/0013164420912318

Zhan, P., Jiao, H., & Liao, D. (2018). Cognitive diagnosis modelling incorporating item response times.(2), 262–286.

Zhan, P., Jiao, H., Man, K, & Wang, L. (2019). Using JAGS for Bayesian cognitive diagnosis modeling: A tutorial.(4), 473–503.

Zhan, P., Liao, M., & Bian, Y. (2018). Joint testlet cognitive diagnosis modeling for paired local item dependence in response times and response accuracy., 607.

Zhan, P., Man, K., Wind, S. A., & Malone, J. (2022). Cognitive diagnosis modeling incorporating response times and fixation counts: Providing comprehensive feedback and accurate diagnosis.. https://doi.org/10.3102/10769986221111085

Zhan, P., & Qiao, X. (2022). Diagnostic Classification analysis of problem-solving competence using process data: An item expansion method.. https://doi.org/10.1007/ s11336-022-09855-9

Zheng, T., Zhou, W., & Guo, L. (in press). Cognitive diagnosis modelling based on response times.

[郑天鹏, 周文杰, 郭磊. (in press). 基于题目作答时间信息的认知诊断模型..]

Zoanetti, N. (2010). Interactive computer based assessment tasks: How problem-solving process data can inform instruction.(5), 585–606.

附录:

S1 参数估计对先验分布的鲁棒性分析

S1.1 高、中和低信息先验分布

S1.1.1 中信息先验分布

在贝叶斯参数估计值中, 先验分布的选择反映了数据分析者对模型参数的信念或已有经验。根据已有数据分析经验以及已有研究结果(如, Man & Harring, 2019; Zhan et al., 2022), 包含适量信息的先验分布(即中信息先验分布)设定如下(对3个C-MCDM通用):

首先, 根据局部独立性假设, 有

其次, 对题目参数而言, 有

然后, 对被试参数而言, 有

再有, 对高阶潜在结构参数而言, 有

S1.1.2 低信息先验分布

低信息先验分布的设定以“无知”为前提, 并以大方差(如, 10)为变异范围。在S1.1.1的基础上, 低信息先验分布设定如下:

其他参数的先验分布保持不变。

S1.1.3 高信息先验分布

高信息先验分布的设定以“先知”为前提, 围绕参数“真值”进行, 并以小方差(如, 0.5)为变异范围。在S1.1.1的基础上, 高信息先验分布设定如下:

其他参数的先验分布保持不变。

S1.2 参数估计一致性

选用正文模拟研究中= 100,= 15,= 0.5条件下生成的数据作为分析数据; 该模拟测验条件属于小样本短测验情境, 理论上, 参数估计结果受到先验分布的影响更大。因此, 随样本量增大及测验长度提高, 参数估计结果受先验分布中所含信息量的影响会逐渐降低(即鲁棒性会增加)。3个模型的参数估计设定(如, 马尔可夫链长)与模拟研究中保持一致。

图S1-S2和表S1分别呈现了3个模型在不同信息量先验分布下各参数的返真性。可发现随着先验分布的信息量的提高, 各参数的返真性均有小幅度提升; 其中, 提升幅度相对较大的是由低信息量先验到中信息量先验时, 而由中信息量先验到高信息量先验的提升幅度微弱。考虑到实际应用中很少使用如此低信息的先验分布且无法像高信息先验分布那样围绕各参数的“真值”进行设定, 中信息先验分布的普适性是相对较高的: 即避免了不实际的“无知”或“先知”, 同时又保证了较高的参数估计精度。因此, 正文中我们选用中信息先验分布进行后续的分析。

整体而言, 当采用包含不同信息量的先验分布时, 每个模型的参数估计结果均较为稳定, 即新模型对不同先验分布具有一定的鲁棒性。

图S1 三模型在不同信息量先验分布下的属性(模式)判准率.

注: N = 样本量; I = 测验长度; CL = 交叉载荷; ACCR = 属性判准率; PCCR = 属性模式判准率.

图S2 三模型在不同信息量先验分布下的潜在能力、潜在加工速度和潜在视觉参与度的返真性

注: N = 样本量; I = 测验长度; CL = 交叉载荷; θ = 高阶潜在能力; τ = 潜在加工速度; ε = 潜在视觉参与度; Bias = 偏差; RMSE = 均方根误差; Cor = 估计值与真值的相关系数.

Joint-cross-loading multimodal cognitive diagnostic modeling incorporating visual fixation counts

ZHAN Peida

(Department of Psychology, College of Teacher Education, Zhejiang Normal University; Key Laboratory of Intelligent Education Technology and Application of Zhejiang Province, Zhejiang Normal University, Jinhua 321004, China)

Students’ observed behavior (e.g., learning behavior and problem-solving behavior) comprises of activities that represent complicated cognitive processes and latent conceptions that are frequently systematically related to one another. Cognitive characteristics such as cognitive styles and fluency may differ between students with the same cognitive/knowledge structure. However, practically all cognitive diagnosis models (CDMs) that merely assess item response accuracy (RA) data are currently incapable of estimating or inferring individual differences in cognitive traits. With advances in technology-enhanced assessments, it is now possible to capture multimodal data, such as outcome data (e.g., response accuracy), process data (e.g., response times (RTs), and biometric data (e.g., visual fixation counts (FCs)), automatically and simultaneously during the problem-solving activity. Multimodal data allows for precise cognitive structure diagnosis as well as comprehensive feedback on various cognitive characteristics.

First, using joint analysis of RA, RT, and FC data as an example, this study elaborated three multimodal data analysis methods and models, including separate modeling (whose model is denoted as S-MCDM), joint- hierarchical modeling (whose model is denoted as H-MCDM) (Zhan et al., 2022), and joint-cross-loading modeling (whose model is denoted as C-MCDM). Following that, three C-MCDMs with distinct hypotheses were presented based on joint-cross-loading modeling, namely, the C-MCDM-θ, C-MCDM-D, and C-MCDM-C, respectively. Three C-MCDMs, in comparison to the H-MCDM, introduce two item-level weight parameters (i.e., φand λ) into the RT and FC measurement models, respectively, to quantify the impact of latent ability or latent attributes on RT and FC. The Markov Chain Monte Carlo method was used to estimate model parameters using a full Bayesian approach. To illustrate the three proposed models’ application and compare them to the S-MCDM and H-MCDM, multimodal data for a real-world mathematics test was used. Data was gathered at a prominent university on the East Coast of the United States in an eye-tracking lab. An= 10 mathematics items test was given to= 93 university students with normal or corrected vision. The test included= 4 attributes, and the related Q-matrix is shown in Figure 3. The data is divided into three modalities: RA, RT, and FC, which were all collected at the same time. The data was fitted to all five multimodal models.

In addition, two simulation studies were conducted further to explore the psychometric performance of the proposed models. The purpose of simulation study 1 was to explore whether the parameter estimates of the proposed models can converge effectively and explore the recovery of parameter estimation under different simulated test situations. The purpose of simulation study 2 was to explore the relative merits of C-MCDMs and H-MCDM, that is, to explore the necessity of considering cross-loading in multimodal data analysis.

The results of the empirical study showed that (1) the C-MCDM-θ has the best model-data fitting, followed by the H-MCDM and the S-MCDM. Although the DIC showed that the C-MCDM-D and C-MCDM-C also fitted the data well, the results were only for reference because some parameter estimates in these two models did not converge; that (2) the correlation coefficients between latent ability and latent processing speed and that between latent ability and latent concentration were weak, making it difficult to fully exploit the theoretical advantages of H-MCDM over S-MCDM (Ranger, 2013). By contrast, since the C-MCDM-θ can directly utilize the information from RT and FC data, the standard error of the estimates of its latent ability was significantly lower than that of the previous two competing models; and that (3) the median of the estimates of φwas less than 0, which indicated that for most items, the higher the participant’s latent ability is, the longer the time it will take to solve the items; and the median of the estimates of λwas higher than 0, which indicated that for most items, the higher the participant’s latent ability is, the more number of fixation counts he/she shown in problem-solving. Furthermore, it should be noted that the estimates of φand λdo not always have the same sign for different items, indicating that the influence of latent abilities on RT and FC has different directions (i.e., facilitation or inhibition) for different items. Furthermore, simulation study 1 indicated that the parameter estimation of the proposed three models could converge effectively and the recovery of model parameters was good under different simulated test situations. The results of simulation study 2 indicated that the adverse effects of ignoring the possible cross- loadings are more severe than redundantly considering the cross-loadings.

Overall, the results of this study indicate that (1) fusion analysis is more suitable for multimodal data that provides parallel information than separate analysis; that (2) through cross-loading, the proposed models can directly use information from RT and FC data to improve the parameter estimation accuracy of latent ability or latent attributes; that (3) the results of the proposed models can be used to diagnose cognitive structure and infer other cognitive characteristics such as cognitive styles and fluency; and that (4) the proposed models have better compatibility with different test situations than H-MCDM.

cognitive diagnosis, multimodal data, item response times, fixation counts, cognitive style, eye-tracking

B841

2021-06-10

* 国家自然科学基金青年基金项目(31900795)和浙江省哲学社会科学规划“之江青年理论与调研专项课题”(22ZJQN38YB)资助。

詹沛达, E-mail: pdzhan@gmail.com