多级属性Q矩阵的验证与估计*

秦春影 喻晓锋

多级属性矩阵的验证与估计*

秦春影1,2喻晓锋1

(1江西师范大学心理学院, 南昌 330022) (2南昌师范学院数学与信息科学学院, 南昌 330032)

多级属性是将诊断测验中传统的二值(即两种水平, 通常定义为0和1)属性定义为多值(多个水平可以为0, 1, …), 它不但可以描述学生对于知识属性是否掌握, 而且可以描述学生在属性上的掌握程度, 这样使得诊断测验能提供给被试更丰富的知识掌握详情。本文将适用于二级属性矩阵的统计量(统计量)拓展到多级属性下的矩阵验证和估计, 在两种常见的条件下, 设计了两种估计算法：联合估计算法和在线估计算法。模拟实验结果表明：联合估计算法适用于对专家界定的初始矩阵进行验证, 当初始矩阵中包含较少的错误时, 通过联合估计算法有很大可能恢复正确的矩阵; 在线估计算法适用于对“新项目”进行属性向量和项目参数的在线标定, 基于一定数量的“基础项目”, 在线估计算法对于新项目的估计也能达到较满意的成功率。实证数据分析则进一步展示了该方法的使用。

多级属性,矩阵, p-DINA模型,统计量

1 引言

随着社会的发展, 教育和心理测验已经不满足于单一的总体评价(overall assessment)。认知诊断评价(cognitive diagnosis assessment, CDA)可以提供学生在知识上的掌握详情, 已受到社会的广泛关注(Leighton & Gierl, 2007; Tatsuoka, 2009; Rupp et al., 2010; 罗照盛, 2019; von Davier & Lee, 2019)。传统的测验, 如基于经典测验理论(classical test theory, CTT)或基于项目反应理论(item response theory, IRT)的测验都仅仅提供学生的总体分数或能力, 除了这个总体评价之外, CDA还可以提供学生的知识状态(knowledge state, KS), 这个知识掌握状态可以对学生的学习、教师的教学和教学效果的评价起到很好的指导和参考作用。

通常情况下, CDA中学生对知识的掌握情况是用0或1来描述, 1表示学生掌握了某个知识, 0表示没有掌握, 即学生对知识的掌握仅仅有2个水平。文献中通常把CDA中细粒度的知识用属性(attribute; Leighton et al., 2004)来描述, 学生在这多个属性上的掌握情况就是学生的KS。因此, 学生的KS通常是一个二值向量。将学生对属性的掌握情况用0和1来描述的好处是相对简单, 容易解释, 但是却也相对粗糙, 不能准确刻画学生在属性上的掌握程度, 因为两个在某属性上的状态都为0的学生之间还是有掌握程度上的区别的。也正是因为如此, 有很多研究者考虑将属性的二种取值考虑设置成多种取值(Karelitz, 2004; von Davier, 2008; Chen & de la Torre, 2013; Sun et al., 2013; 蔡艳, 涂冬波, 2015; 涂冬波, 蔡艳, 2015; 詹沛达等, 2016; Zhan et al., 2020; Shang et al., 2021)。实际应用中, 有很多情况都是对知识属性的多水平要求和考查, 比如《全日制义务教育数学课程标准(修改稿)》中就使用了“了解(认识)”、“理解”、“掌握”和“运用”这4个顺序类别词汇来表述知识技能目标的不同水平。因此, 多级属性能够对学生做出更为精细地划分, 将属性定义成多级的诊断测验具有现实应用价值和前景。

也正是因为如此, 研究者们对基于多级属性的CDA展开了研究, 有针对性地开发了诊断模型, 比如Karelitz (2004)构建了基于顺序类别属性编码(ordered-category attribute coding, OCAC)的诊断模型OCAC-DINA, 并且对矩阵中存在缺失时的参数估计和分类进行研究; 还有基于其它诊断模型所开发的多级属性模型, 像RRUM下的多级属性模型(Templin, 2004), LCDM下的多级属性模型(Templin & Bradshaw, 2014); GDM下的多级属性模型(Haberman et al., 2008; von Davier, 2008); Zhan等人(2020)构建了高阶的多级属性的诊断模型等; 与前面这些研究不同的是, Shang等人(2021)借鉴多维IRT的思想, 定义连续的多级属性, 并且构建了可以处理连续多级属性的诊断模型。同传统的CDA一样, 多级属性CDA中的矩阵的作用也十分关键, 它的正确性会直接影响模型参数的识别、被试的分类乃至整个测验的信度和效度。并且更重要的是, 在实际应用中, 仅仅由专家界定的矩阵很容易出现错误或专家意见不一致的情况(de la Torre, 2008; DeCarlo, 2012; Liu et al., 2012; 喻晓锋等, 2015a; Yu & Cheng, 2020)。从目前已有的研究来看, 研究者们采用的多级属性矩阵大都是由专家界定或模拟生成, 通常假定它是正确的, 没有对它的正确性或合适性进行验证, 还缺乏对多级属性矩阵的验证和估计方法进行研究。因此, 迫切需要研究客观的方法来对其正确性进行验证或估计。本研究拟将适合二级属性下矩阵的验证和估计方法拓展到适合多级属性矩阵的情况, 研究客观的验证或估计多级属性矩阵的方法, 以期能促进多级属性CDA的发展。

2 多级属性Q矩阵及诊断模型

在正式介绍多级属性矩阵的估计算法之前, 首先对多级属性矩阵及对应的诊断模型进行介绍。

2.1 多级属性Q矩阵

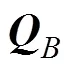
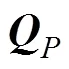
如果属性按按传统的二级方式, 用0作为截断点来对属性进行划分, 则其所对应的矩阵如(2)所示。

2.2 多级属性下的诊断模型

已开发的适合多级属性的诊断模型主要有OCAC-DINA (Karelitz, 2004), LCDM下的多级属性模型(Templin & Bradshaw, 2014), GDM对应的多级属性诊断模型(Haberman et al., 2008; von Davier, 2008), 基于G-DINA框架下的多级属性模型, 比如Chen和de la Torre (2013), 蔡艳和涂冬波(2015), 高阶的多级属性模型(Zhan et al., 2020), 连续的多级属性诊断模型(Shang et al., 2021)等。在这里, 为节省篇幅, 仅仅介绍与本文有关的pG-DINA和p-DINA模型。

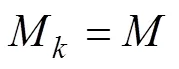
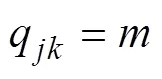
3 多级属性Q矩阵的估计方法

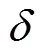
3.1 基于SP统计量的多级属性Q矩阵估计

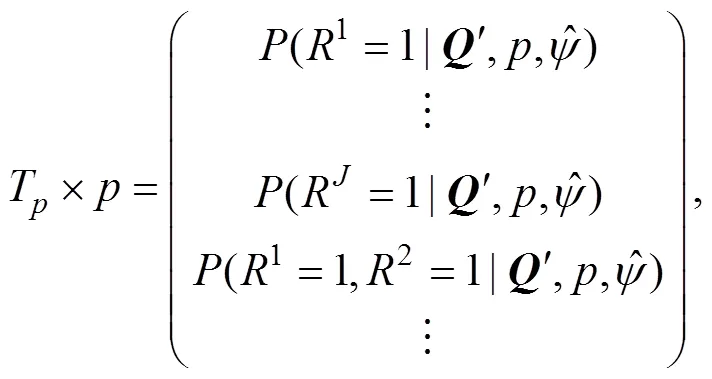
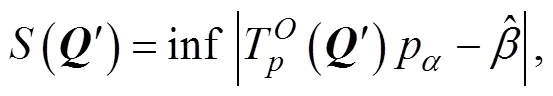
下面介绍适合于前面提到的两种应用情境的算法。

3.2 基于SP统计量的联合估计算法JE

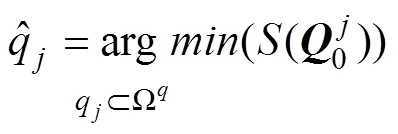
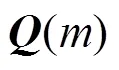
3.3 基于SP统计量的在线估计算法OE

JE算法需要专家已经对测验中的所有项目属性均已界定, 只是其中包含错误。不同的是, OE算法只需要专家对少部分项目已经界定, 对剩余的项目未界定(可以是以下三种情况：新编制的项目需要界定属性、专家之间对属性界定持不同意见的项目、属性定义不确定或有怀疑的项目), 在这种情况下, 可以采用OE算法进行估计。

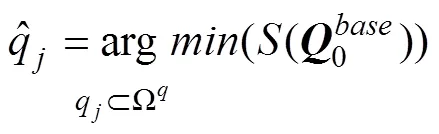
4 研究设计

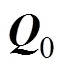
4.1 对于JE算法

4.2 对于OE算法

4.3 数据模拟

4.3.1矩阵

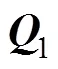
4.3.2 项目参数

4.3.3 被试参数

4.3.4 作答数据

基于真实的矩阵、项目参数和被试参数, 按照p-DINA模型模拟作答数据。

4.3.5 初始矩阵

4.3.6 参数估计

数据的模拟和分析采用matlab编写程序完成, 每种实验条件重复100次, 最后取100次的平均值作为最终的结果。

4.3.7 评价指标

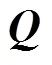
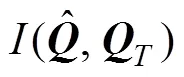
平均迭代次数是对100次估计的总迭代次数计算平均值。

与平均迭代次数类似, 我们同样也分别记录了两种方法的平均执行时间, 它也描述了对应方法的计算效率, 具体计算公式为

4.4 研究1：多级属性Q矩阵和参数的联合估计

联合估计适合的测验情形是：专家已对测验项目都已界定, 只是对部分项目的属性定义尚不确定、可能界定错误或意见不统一时使用。采用JE算法可以对矩阵进行验证, 并且输出建议的矩阵。下面分两种错误类型进行介绍。

4.4.1 仅仅存在属性值界定错误时的联合估计

在实际应用中, 专家在界定某些项目的属性值时出现分歧或错误的情况, 即前面所介绍的错误I, 这是一种相对简单的情形。因此本研究考察当初始矩阵中有部分项目仅仅出现属性低估或高估的情况(不包括低估至0或从0高估的情况)。

学生在测验中的作答模拟是按真实矩阵完成, 只是在分析数据时采用包含错误的“初始矩阵”作为输入, 采用JE算法来实现对矩阵、项目参数和被试参数的联合估计, 最后比较算法估计得到的矩阵与真实矩阵之间的差异, 若完全一致,则估计成功, 否则估计失败, 并且统计估计过程中的迭代次数。

4.4.2 存在属性值错误、含多余属性或缺失必要属性时的联合估计

相对来说, 错误II是比错误I更严重的错误, 因为不但会出现属性低估和高估, 同时还会出现将未考察的属性包含进来, 也可能会出现将考察的属性遗漏, 这在实际应用也是有可能出现的, 错误I可以看成是错误II的一种特殊情形。因此本研究考察当初始矩阵出现错误II时JE算法的表现。

4.5 研究2：多级属性Q矩阵和参数的在线估计

在线估计算法OE适合的另一种测验情形, 即仅仅少部分项目被正确界定, 有大批项目需要定义属性向量的情况, 比如对编制的一批新题进行界定(包括属性向量和参数), “新项目”的属性向量不需要专家进行初始界定, 可以按随机方式生成, 在这种情况下, 可以借助已有项目的信息, 完成对新项目的界定。

界定时需要学生同时作答“基础项目”和“新项目”, 估计时固定“基础项目”的属性向量, 只需要估计“新项目”的属性向量。为了充分利用已有信息, 减少“噪音”信息引起的“遮罩效应”(masking effect; Fung, 1993; Yuan & Zhong, 2008)带来的负面影响, 估计时采用每次只加入一个“新项目”的增量式估计的方式进行。并且, 为了降低由于“基础题”的质量所带来的影响, 在OE算法结束后, 对整个矩阵再使用JE算法进行整体估计, 提高估计的成功率。最后比较算法估计得到的矩阵与真实矩阵之间的差异, 若完全一致, 则估计成功, 否则估计失败, 并且统计估计过程中的迭代次数。

需要注意的是, OE算法中是指完成所有的“新项目”估计后, 如果“新项目”没有估计成功, 则对包含“基础项目”和“新”项目的矩阵用JE算法进行联合估计, 因此从这个角度来看, OE算法中的迭代次数与JE算法中一样, 也是指对所有项目完成一次估计的次数。

4.6 试验结果

4.6.1 JE算法的估计结果

表1～表4是JE算法在项目数(30, 15)和错误类型(I和II)时的估计结果, 从结果可以看出, JE算法在估计矩阵时, 其执行效率和正确率受到多方面因素的影响, 比如：被试人数, 测验的项目数, 包含的错误项目数等的影响。研究1和研究2是分别安排在两台云服务器上运行的, 服务器的具体配置是：CPU是2颗至强E5-2697, 十二核心; 内存类型DDR5, 容量是64 G; 硬盘类型是固态, 容量512 G。从算法的执行效率来看, 虽然算法的搜索空间已经下降了很多, 但是依然有较大的搜索空间, 各种条件下的平均执行时间仍然较大, 最低情况下需要一天的时间(89182.33秒)。从算法的正确率来看, 相对来看, 测验项目数对于正确率的影响很大, 测验项目从30下降到15, 估计成功率平均下降了61.67%。

从表1和表2中可以看出, 被试人数和测验项目数都与矩阵估计成功率有正向的相关关系, 而错误项目数与矩阵估计成功率则有负向的相关关系。根据本研究中的条件, 被试人数为2000, 测验项目数为30, 可以达到较好的估计结果。具体来说, 对于估计成功率,矩阵包含30题时各条件下都能达到80%以上, 而15题时最好的情况都要小于60%。从迭代次数来看, 测验项目数为15时, 各样本条件下需要的平均迭代次数小于2.5, 而当项目数达到30时, 对应需要的迭代次数超过3。图1和图2进一步展示了JE算法的表现随着错误界定项目数发生变化的趋势。

表3和表4分别是测验项目数为30, 15, 并且矩阵中包含错误类型II时的估计结果。可以看出, 一方面被试人数的增加可以提高JE算法的估计成功率, 比如测验长为30, 错误项目数为3和5时, 被试人数从1000提高到4000, 估计成功率分别提高了7%和13%。另一方面, 被试人数和错误项目数会对估计成功率会产生交互作用, 因为当测验长度只有15, 错误项目数3和5, 人数从1000提高到4000, 估计成功率分别提高了18%和5%, 此时人数的增加对低错误项目数影响更大, 这与测验长度为30时的情况正好相反。图3和图4是测验项目为15题时JE算法的表现随着错误界定项目数发生变化的情况。

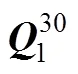
表1 错误类型I, 时JE算法的估计成功率和平均迭代次数

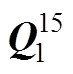
表2 错误类型I, 时JE算法的估计估计成功率和平均迭代次数

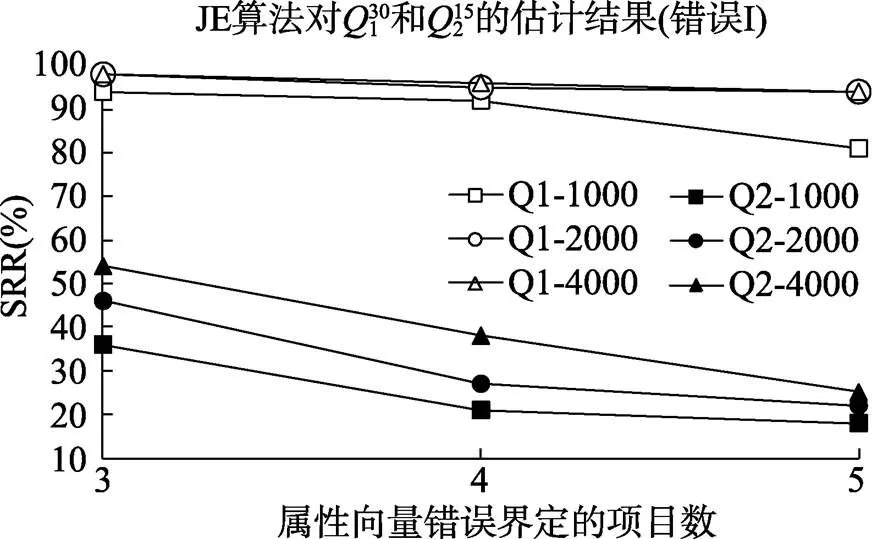
图1 错误类型I时, JE算法的估计结果

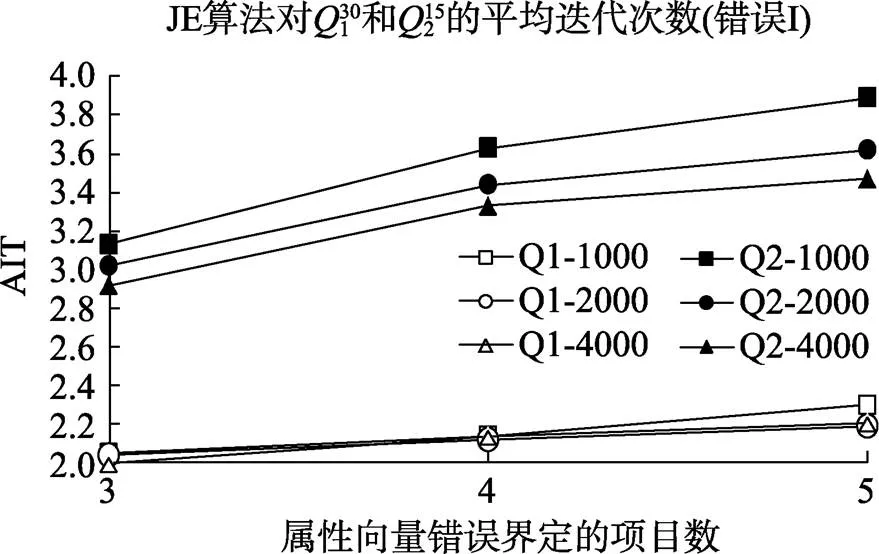
图2 错误类型I时, JE算法的迭代次数

表3 错误类型II, 时JE算法的估计成功率平均迭代次数

表4 错误类型II, 时JE算法的估计成功率和平均迭代次数

综合表1, 表2, 表3和表4可以看出, 一方面, 当错误类型为II时, 相同人数、题目条件下要略低于错误类型I时的估计成功率, 并且相应的迭代次数也要更多, 这是因为错误类型II时, 项目属性向量可能的取值空间更大所导致的; 另一方面, 从平均运行时间来看, 相对于错误类型I, 固定其它条件时错误类型II各对应的实验条件需要相对更多的运行时间, 这一点是和更大的迭代次数相一致的。

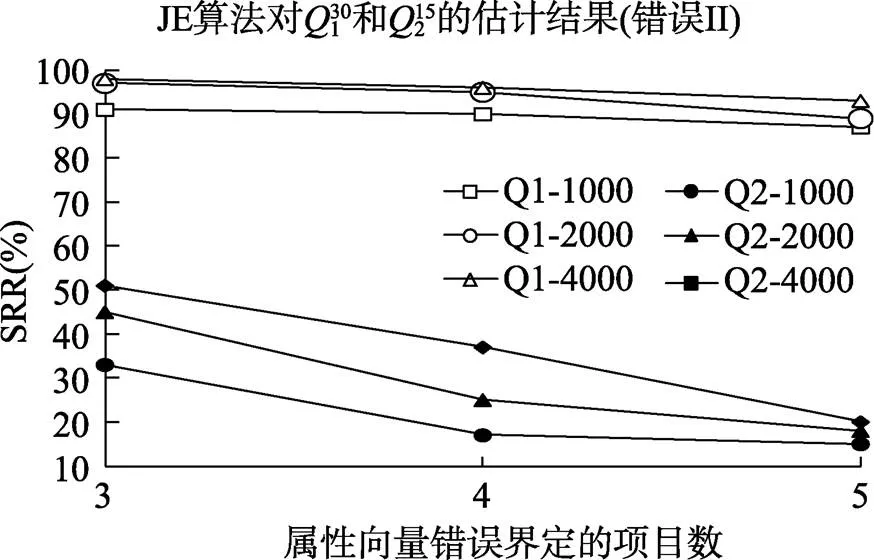
图3 错误类型II时, JE算法的估计结果

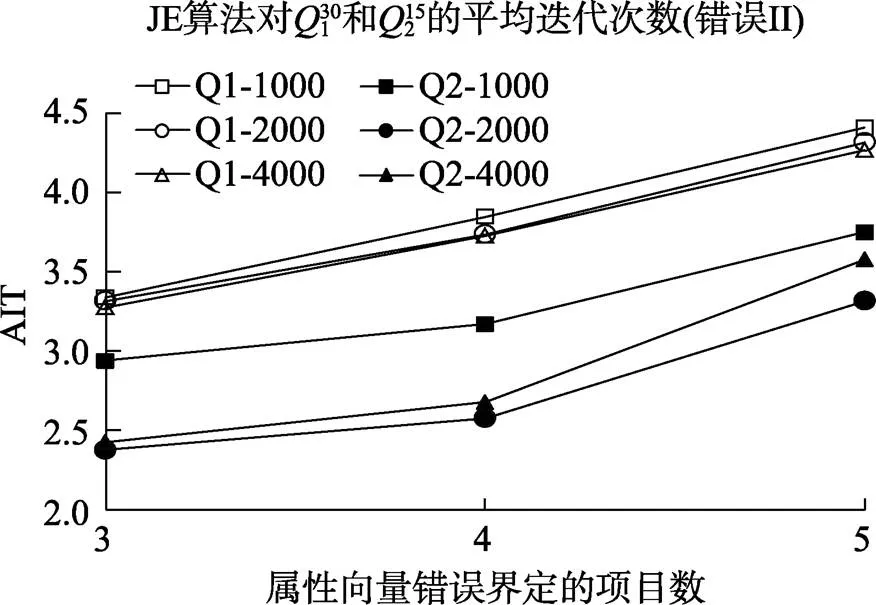
图4 错误类型II时, JE算法的迭代次数

综合图1、图2、图3和图4, 随着矩阵中包含的错误项目数增加, 不论是错误类型I还是错误类型II, JE算法估计的成功率在下降, 所需要的迭代次数在增加。

4.6.2 OE算法的估计结果

从图5～图8可以看出, 当测验项目数从30降到15时, 算法所需要的迭代次数会有较大的增加, 比如基础题为10个, 1000人, 长度30和15的测验所需要的迭代次数分别为0.74和1.06。

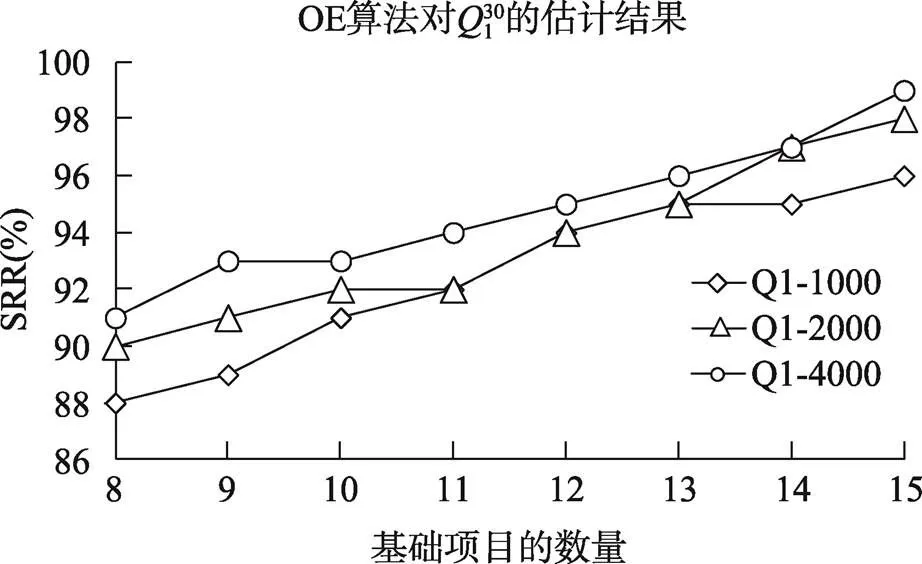
图5 OE算法在的估计结果

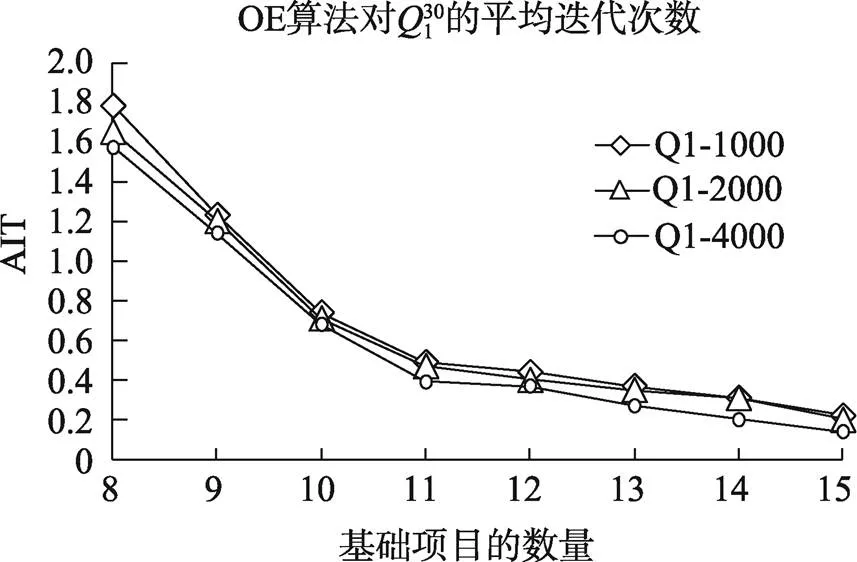
图6 OE算法在的迭代次数

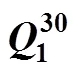
表5 时OE算法的估计成功率和平均迭代次数

注：OE算法中的平均迭代次数是指在对数据进行整体估计时的平均迭代次数, 如果估计过程不需要整体估计即已成功完成, 则该批数据的迭代次数为0。

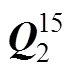
表6 时OE算法的估计估计成功率和平均迭代次数

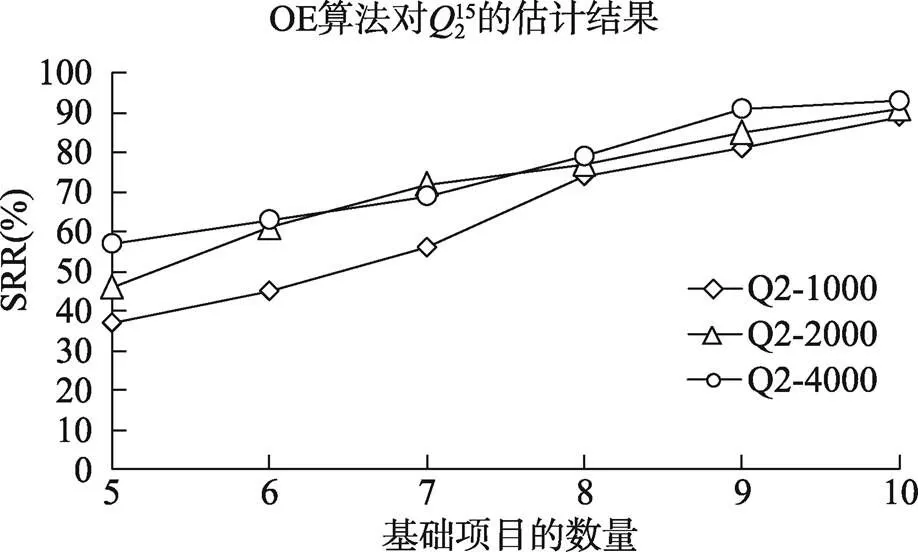
图7 OE算法对的估计结果

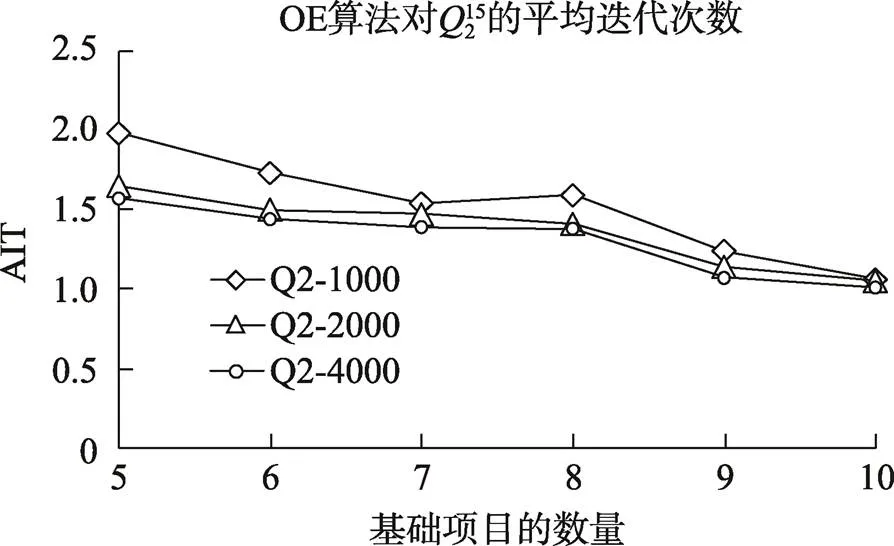
图8 OE算法对的平均迭代次数

5 实证数据分析

为了进一步评价两种算法的性能, 将它们应用到一批实证数据上。这批实证数据是来自于某市高中的一次月考, 选取了数学试卷中与概率有关的试题。这部分测试题考察了随机事件, 样本空间, 古典概率, 使用频数估计概率共4个属性。每个属性有5个连续的掌握类别：不了解, 了解, 理解, 掌握和应用, 分别用0, 1, 2, 3, 4表示。基于这4个属性, 由学科专家共编制了20个题, 一共有1960个考生完成了测验。

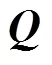
表7 概率数据对应的原始Q矩阵

对于OE算法, 我们选择了初始矩阵中的5个题目(表A4中灰色背景显示的题目), 选择这5个题目的原因是学科专家对这5道题的属性定义完全一致, 并且它们在JE算法的建议矩阵中也得到了验证。余下的15道题作为“新题目”, 将它们逐个用OE算法进行估计。当所有的“新题目”完成了估计, 再用JE算法对所有题目进行联合估计, 这样就得到了OE算法建议的矩阵, 如网络版附录中的表A4所示。可以看出, OE算法建议修改6个题目, 共涉及6个属性。除了第19题之外, 由JE和OE两种算法得到的建议矩阵是完全一致的。对于第19题, 专家界定的初始向量为[0 0 4 2], JE和OE算法得到的属性向量分别是[0 0 3 3]和[0 0 4 3]。在与5位一线的教师进行讨论之后, 他们其中的4位都倾向于同意OE算法得到的结果, 即将第4个属性初始定义的水平2修改为水平3。

6 讨论与进一步的研究方向

虽然JE和OE算法在模拟条件下取得了较好的结果, 即使如此, JE和OE算法仍然需要在更复杂的情况中去验证, 对于JE算法, 这里只考虑“初始矩阵”中包含的错误项目较少, 对于更多错误时的估计或者所能容忍的最大错误项目数量需要进一步研究; 对于OE算法, 研究中随机选择了100批“基础项目”, 这100批“基础项目”的质量有好有坏, 并没有考虑“基础项目”的质量对于估计的影响, 如果进一步研究“基础项目”的设计, 使之更有利于“新项目”的估计, 就像诊断测验中的矩阵设计一样, 在基础题中加入“可达矩阵”对于矩阵估计的影响等(Chen et al., 2015; 丁树良等, 2019; 彭亚风等, 2016, 2018; Gu et al., 2018; Gu & Xu, 2021), 应该是很有意义的工作。本研究中无论是JE还是OE算法, 只考虑了两种错误类型, 实际上, 还有可能存在其它的错误类型, 未来需要对其它更多可能的情况进行研究。另外, 现实的测验情境往往是很复杂的, 比如考生可能是存在多种解题策略的, 因此, 结合多种策略的诊断测验中矩阵的估计需要进一步考虑(黄玉等, 2019)。测验的属性间很可能存在某种层级关系(喻晓锋等, 2021), 属性间存在层级关系时的多值矩阵估计也是未来需要研究的方向。

基于S统计量的矩阵估计一个不足之处在于需要花费较多的时间, 这对于实际应用可能是一个潜在的缺陷, 未来对提出的方法进行时间效率上的改进或研究时间效率更高的方法都值得进一步研究。比如Yu和Cheng (2020)的研究表明, 0-1计分下基于残差统计量的统计量比基于统计量在运行效率上有优势, 因此将基于残差的统计量拓广到多值属性诊断测验的矩阵估计值得考虑; 未来也需要进一步考虑一些非参数的方法, 因为它们通常对于样本量的要求较小, 并且有执行效率上的优势(刘娜等, 2021); 将基于深度学习等一些算法拓广到多值属性诊断测验的矩阵估计(张玉柳等, 2021; Li et al., 2022)也需要深入研究。

实证数据的分析表明, 本研究中提出的基于统计量的联合估计算法和在线估计算法可以在实际中应用, 并且结果显示专家对于题目属性向量的错误定义更容易出现在高估或低估属性的水平上, 不太容易出现完全缺失某个属性或包含额外的属性等更严重的情况。OE算法的一个副产品是同时将新项目的参数进行了估计, 并且它能保证与基础项目的参数处于同一个尺度上。将属性间的关系纳入考虑需要进一步研究, 未来也需要将算法应用到其它的诊断模型中(Ma & de la Torre, 2019; Zhan et al., 2020)。

Cai, Y., & Tu, D. B. (2015). Extension of cognitive diagnosis models based on the polytomous attributes framework and their Q-matrices designs.(10), 1300–1310.

[蔡艳, 涂冬波. (2015). 属性多级化的认知诊断模型拓展及其Q矩阵设计.(10), 1300–1310.]

Chen, J. S., & de la Torre, J. (2013). A general cognitive diagnosis model for expert-defined polytomous attributes.(6), 419–437.

Chen, Y. X., Liu, J. C., Xu, G. J., & Ying, Z. L. (2015). Statistical analysis of Q-matrix based diagnostic classification models.(510), 850–866.

Chung, M.-T. (2014).(Unpublished doctoral dissertation), Columbia University, New York.

DeCarlo, L. T. (2012). Recognizing Uncertainty in the Q-Matrix via a Bayesian Extension of the DINA Model.(6), 447–468.

de La Torre, J. (2008). An empirically based method of Q-matrix validation for the DINA model: Development and applications.(4), 343–362.

de la Torre, J. (2009). DINA model and parameter estimation: A didactic.(1), 115–130.

de la Torre, J. (2011). The generalized dina model framework.(2), 179-199.

de la Torre, J., & Chiu, C. Y. (2016). A general method of empirical Q-matrix validation.,(2), 253–273.

Ding, S. L., Luo, F., Wang, W. Y., & Xiong, J. H. (2019). The designing cognitive diagnostic test with dichotomous scoring.(5), 441–447.

[丁树良, 罗芬, 汪文义, 熊建华. (2019). 0-1评分认知诊断测验设计.(5), 441–447.]

Fung, W.-K. (1993). Unmasking outliers and leverage points: A confirmation.(422), 515–519.

Gu, Y. Q., Liu, J. C., Xu, G. J., & Ying, Z. L. (2018). Hypothesis testing of the Q-matrix,(3), 515–537.

Gu, Y. Q., & Xu, G. J. (2021). Sufficient and Necessary Conditions for the Identifiability of the Q-matrix., 449–472.

Haberman, S. J., von Davier, M., & Lee, Y.-H. (2008).(ETS Research Report no. RR-08-45). Princeton, NJ: Educational Testing Service.

Huang, Y., Luo, F., Xiong, J. H., Ding, S. L., & Gan, D. W. (2019). The multiple-strategy cognitive diagnosis method with polytomous scoring.(4), 376–381.

[黄玉, 罗芬, 熊建华, 丁树良, 甘登文. (2019). 多级评分多策略认知诊断方法.(4), 376–381.]

Karelitz, T. M. (2004).(Unpublished doctoral dissertation), University of Illinois at Urbana-Champaign.

Leighton, J. P., & Gierl, M. J. (2007).. Cambridge University Press.

Leighton, J. P., Gierl, M. J., & Hunka, S. M. (2004). The attribute hierarchy method for cognitive assessment: A variation on Tatsuoka’s rule-space approach.(3), 205–237.

Li, C. C., Ma, C. C., & Xu, G. J. (2022). Learning large Q-matrix by restricted Boltzmann machines.. https://doi.org/10.1007/s11336-021-09828-4.

Liu, J. C., Xu, G. J., & Ying, Z. L. (2012). Data driven learning of Q matrix.(7), 548–564.

Liu, J. C., Xu, G. J., & Ying, Z. L. (2013). Theory of self-learning Q-matrix.(5A), 1790–1817.

Liu, N., Liu, X. L., Li, J. J., Zeng, P. F., Yu, X. J., & Kang, C. H. (2021). Constructing a non-parametric Q-matrix correction method based on Manhattan distance.(6), 634–641.

[刘娜, 刘芯伶, 李俊杰, 曾平飞, 俞向军, 康春花. (2021). 基于曼哈顿距离构建非参数Q矩阵修正方法.(6), 634–641.]

Luo, Z. S. (2019).. Beijing Normal University publishing group.

罗照盛. (2019).北京师范大学出版集团.

Ma, W., & de la Torre, J. (2019). An empirical Q-matrix validation method for the sequential generalized DINA model.(1), 142–163.

Peng, Y. F., Luo, Z. S., Li, Y. J., Gao, C. L. (2018). Optimization of test design for examinees with different cognitive structures.(1), 130–140.

[彭亚风, 罗照盛, 李喻骏, 高椿雷. (2018). 不同认知结构被试的测验设计模式.(1), 130–140.]

Peng, Y. F., Luo, Z. S., Yu, X. F., Gao, C. L., Li, Y, J. (2016). The optimization of test design in Cognitive Diagnostic Assessment.(12), 1600–1611.

[彭亚风, 罗照盛, 喻晓锋, 高椿雷, 李喻骏. (2016). 认知诊断评价中测验结构的优化设计.(12), 1600–1611.]

Qin, C. Y., Jia, S., Fang, X. W., & Yu, X. F. (2020). Relationship validation among items and attributes,(18), 3360–3375

Qin, C. Y., Zhang, L., Qiu, D., Huang, L., Geng, T., Jiang, H., ... Zhou, J. (2015). Model identification and Q-matrix incremental inference in cognitive diagnosis.,, 66–76.

Rupp, A. A., Templin, J., & Henson, R. A. (2010).Guilford Press.

Shang, Z. R., Erosheva, E. A., Xu, G. J. (2021). Partial-masterycognitive diagnosis models.(3), 1529 –1555.

Sun, J. N., Xin, T., Zhang, S. M., & de la Torre, J. (2013). A polytomous extension of the generalized distance discriminatingmethod.(7), 503–521.

Tatsuoka, K. K. (2009).. Routledge.

Templin, J. L. (2004).(Unpublished doctoral dissertation), University of Illinois at Urbana-Champaign.

Templin, J. L., & Bradshaw, L. (2013). Measuring the reliability of diagnostic classification model examinee estimates.(2), 251–275.

Templin, J. L., Bradshaw, L. (2014). The use and misuse of psychometric models.(2), 347–354.

Tu, D. B., & Cai, Y. (2015). The development of CD-CAT with polytomous attributes.(11), 1405–1414.

[涂冬波, 蔡艳. (2015). 基于属性多级化的认知诊断计算机化自适应测验设计与实现.(11), 1405–1414.]

von Davier, M. (2008). A general diagnostic model applied to language testing data.(2), 287–307.

von Davier, M., & Lee, Y.-S. (2019).. Cham: Springer International Publishing.

Wang, D. X., Cai, Y, & Tu, D. B. (2020). Q-matrix estimation methods for cognitive diagnosis models: Based on partial known Q-matrix,, 1–13. https://doi.org/10.1080/00273171.2020.1746901.

Xiang, R. (2013).(Unpublished doctoral dissertation), Columbia University, New York.

Xu, G.-J. (2013).(Unpublished doctoral dissertation), Columbia University, New York.

Yu, X. F., & Cheng, Y. (2020). Data-driven Q-matrix validation using a residual‐based statistic in cognitive diagnostic assessment.(1), 145–179.

Yu, X. F., Luo, Z. S., Gao, C. L., Li, Y. J., Wang, R., & Wang, Y. T. (2015a). An item attribute specification method based on the likelihood D2 statistic.(3), 417–426.

[喻晓锋, 罗照盛, 高椿雷, 李喻骏, 王睿, 王钰彤. (2015a). 使用似然比D2统计量的题目属性定义方法.(3), 417–426.]

Yu, X. F., Luo, Z. S., Qin, C. Y., Gao, C. L., & Li, Y. J. (2015b). Joint estimation of model parameters and Q-matrix based on response data.(2), 273–282.

[喻晓锋, 罗照盛, 秦春影, 高椿雷, 李喻骏. (2015b). 基于作答数据的模型参数和Q矩阵联合估计.(2), 273–282.]

Yu, X. F., Ma, Y. F., Luo, Z. S., & Qin, C. Y. (2021). The attribute hierarchical structure learning based on K2 algorithm.(4), 376–383.

[喻晓锋, 马奕帆, 罗照盛, 秦春影. (2021). 基于K2算法的属性层级结构学习研究.(4), 376–383.]

Yuan, K.-H., & Zhong, X. (2008). Outliers, leverage observations, and influential cases in factor analysis: Using robust procedures to minimize their effect.(1), 329–368.

Zhan, P. D., Bian, Y. F., Wang, L. J. (2016). Factors affecting the classification accuracy of reparametrized diagnostic classification models for expert-defined polytomous attributes.(3), 318–330.

[詹沛达, 边玉芳, 王立君. (2016). 重参数化的多分属性诊断分类模型及其判准率影响因素.(3), 318–330.]

Zhan, P. D., Wang, W., Li, X. M. (2020). A partial mastery, higher-order latent structural model for polytomous attributesin cognitive diagnostic assessments., 328–351.

Zhang, Y. L., Zhao, B., & Tao, J. H. (2021). The study on students' cognitive state based on fuzzy cognitive diagnostic framework.(5), 452–459.

[张玉柳, 赵波, 陶金洪. (2021). 基于模糊认知诊断模型的学生认知状态研究.(5),452–459.]

附录：

附表A1 30题对应的矩阵130

附表A2 15题对应的矩阵215

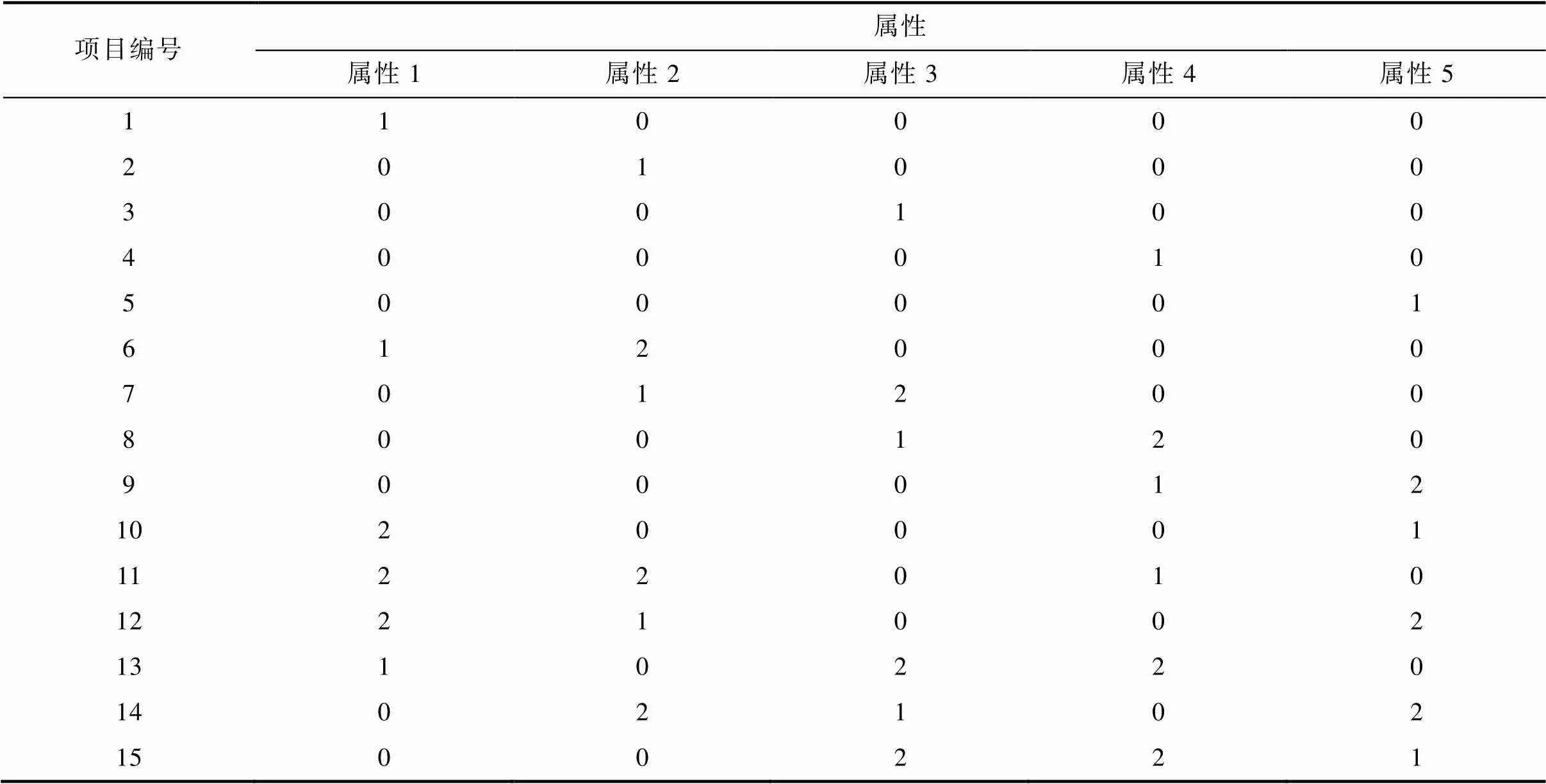
项目编号属性 属性1属性2属性3属性4属性5 110000 201000 300100 400010 500001 612000 701200 800120 900012 1020001 1122010 1221002 1310220 1402102 1500221

附表A3 由JE算法得到概率论数据的建议-matrix

注：表格中用粗斜体显示的元素表示JE算法所修改后的属性取值

附表A4 由OE算法得到概率论数据的建议-matrix

注：阴影显示对应的题目表示OE算法中的“基础题”, 余下的题目对应的是需要估计的“新题”。粗斜体显示元素表示OE算法所修改后的属性取值。加星号的题目表示由OE算法给出的建议值与JE算法给出的建议值不一致的题目。

Validation and estimation of expert-defined-matrix with polytomous attribute

QIN Chunying1,2, YU Xiaofeng1

(1School of Psychology, Jiangxi Normal University, Nanchang, 330022, China) (2School of Mathematics and Information Science, Nanchang Normal University, Nanchang 330032, China)

Cognitive diagnosis has recently gained prominence in educational assessment, psychiatric evaluation, and many other disciplines. Generally, entries in the-matrix of traditional cognitive diagnostic tests are binary (two levels, defined as 0 and 1). Polytomous attributes (multi-levels, defined as 0, 1, …), particularly those defined as part of the test development process, can provide additional diagnostic information. Compared to binary attributes, polytomous attributes can not only describe the student's knowledge profile, but can provide more extensive details.

As we all know,-matrix impacts the accuracy of cognitive diagnostic assessment greatly. Research on the effect of parameter estimation and classification accuracy caused by the error in-matrix already existed, and it turned out that-matrix gotten from expert definition or experience was more easily subject to be affected by subjective factors, lead to a misspecified-matrix. Under this circumstance, it’s urgently needed to find more objective polytomous-attribute-matrix verification and inference methods.

The present research proposes the verification and estimation of expert-defined polytomous attribute-matrix based on the polytomous deterministic inputs, noisy, ‘‘and’’ gate (p-DINA) model. We intend to extend the methods adapted to binary-matrix verification and estimation to polytomous attribute-matrix, and the proposed methods which can be used in different conditions are joint estimation and online estimation. Simulation results show that: the joint estimation algorithm can be applied to the-matrix validation which needs an initial-matrix defined by experts, the online estimation algorithm can be applied to online estimate the “new items” based on a certain number of “based items”. Under the various settings in the simulations, the two estimation algorithms can recover the correct polytomous-attribute-matrix at a high probability. Empirical study also indicates that the two proposed algorithms can be applied in-matrix validation or estimation for CDA with polytomous attributes.

polytomous attribute,-matrix, p-DINA model, S statistics

2021-10-06

* 全国教育科学规划项目(BGA210060); 教育部教育考试院“十四五”规划支撑专项课题(NEEA2021050);江西省社会科学基金项目(21JY06); 江西省高校人文社会科学项目(XL20202); 南昌市教育大数据智能技术重点实验室(2020-NCZDSY-012); 江西省教育厅科技项目(GJJ212602, GJJ191691, GJJ191128)资助。

喻晓锋, E-mail: xyu6@jxnu.edu.cn

B841