基于颜色复杂度和结构张量的恰可察觉失真模型

王 闯, 王永芳, 练俊杰

(上海大学通信与信息工程学院, 上海 200444)

人眼的感知能力是有限的, 当图像信号的失真程度没有超过某一个阈值时, 人眼是察觉不到原始信号与重建信号之间的差异的, 该值被称为恰可察觉失真(just noticeable distortion,JND)阈值, 可以用来表示图像中的视觉冗余程度. 近年来, JND 模型已被被广泛应用于视频图像编码[1]、数字水印[2]、图像增强[3]、质量评估[4]等方面.

传统的JND 模型主要分为2 大类: 像素域JND 模型和变换域JND 模型. Yang 等[5]考虑到背景亮度掩蔽效应和对比掩蔽效应, 提出了非线性叠加掩蔽模型(nonlinear additivity model for masking, NAMM); Liu 等[6]考虑了纹理和边缘各自的掩蔽作用, 将图像分解为纹理图像和结构图像, 分别计算各自的纹理掩蔽效应和边缘掩蔽效应; Wu 等[7]利用人眼对不规则内容不敏感的特性, 将图像分为有序部分和无序部分, 并基于自由能原理对无序内容进行了JND 阈值估计. 考虑到模式复杂度与掩蔽效应之间有较大的相关性, Wu 等[8]将其作为空间掩蔽效应的另一个因素, 改进对比掩蔽效应; Zeng 等[9]将图像进一步分为结构图像、有序纹理图像和无序纹理图像, 分别估计各个部分的JND 阈值, 同时还引入了显著性模型.

由于视频图像的压缩通常在离散余弦变换(discrete cosine transform, DCT)域上进行, 因此变换域JND 模型以DCT 域JND 模型为主. Wei 等[10]考虑到空间敏感度函数效应、背景亮度掩蔽效应、纹理掩蔽效应和时域掩蔽效应, 提出了经典的DCT 域JND 模型. Wan 等[11]提出了基于方向选择性原理的JND 模型, 根据方向规律性和频率纹理能量对DCT 块进行分类,改进对比度掩蔽效应; Wang 等[12]将无序隐藏效应引入到DCT 域中, 根据每个变换块的无序性来估计JND 阈值; Wang 等[13]考虑到视觉注意力机制和中心凹效应, 建立了自适应加权模型并运用到JND 模型中.

近年来, 结合深度学习的JND 模型被提出. Ki 等[14]提出了基于学习的恰可察觉量化失真(just noticeable quantization distortion, JNQD)模型, 利用卷积神经网络(convolutional neural network, CNN)进行训练, 针对不同的量化参数(quantizer parameter, QP)值调整JND阈值; Liu 等[15]提出了基于深度学习的图像级JND 模型, 利用图像之间的相关性对JND 阈值进行预测.

JND 阈值不仅与图像的背景亮度、对比度有关, 还与颜色特征、局部结构有关. 上述模型虽然在原有模型的基础上提高了JND 阈值估计的准确性, 但是没有充分考虑到图像的颜色特征和结构特征. 针对上述问题, 本工作提出了一种基于颜色复杂度和结构张量的JND 模型.首先, 将输入图像转换到LAB 颜色空间, 利用三通道上的像素信息计算各个区域的颜色复杂度, 并转换为与人眼视觉敏感度相关的权值, 与对比掩蔽模型结合以提升模型的准确性; 然后,将利用颜色复杂度调制的对比掩蔽模型与亮度掩蔽模型叠加, 得到基于颜色复杂度JND(color complexity based JND, CJND)的模型. 此外, 由于结构张量矩阵和特征值能够描述局部区域不同的结构特征[16-18], 故建立了基于张量的结构特征的调制因子. 最后, 将CJND 模型和基于张量结构特征的调制因子结合, 得到本工作所提出的基于颜色复杂度和结构张量JND(color complexity and structure tensor based JND, CSJND)模型.

1 基于颜色复杂度和结构张量的JND 模型

本工作提出的CSJND 模型如图1 所示. 首先, 将图像从RGB 颜色空间转换到LAB 颜色空间, 然后分别计算亮度掩蔽模型、对比掩蔽模型和颜色复杂度, 将基于颜色复杂度的视觉加权系数和对比掩蔽模型结合, 再与亮度掩蔽模型叠加; 同时, 计算图像的结构张量矩阵的特征值λ2, 建立结构特征的调制因子; 最后, 将二者结合建立CSJND 模型, 定义如下:

式中: CJND 为基于颜色复杂度的JND 模型;FST为基于张量的结构特征的调制因子.

1.1 基于颜色复杂度的CJND 模型

CJND 模型由亮度掩蔽模型、对比掩蔽模型和颜色复杂度构成(见图1). 颜色复杂度可以反映局部区域的颜色变化信息, 描述人眼对各区域的视觉敏感程度[19]. 将颜色复杂度和对比掩蔽模型进行加权, 再与亮度掩蔽模型结合, 其计算公式为

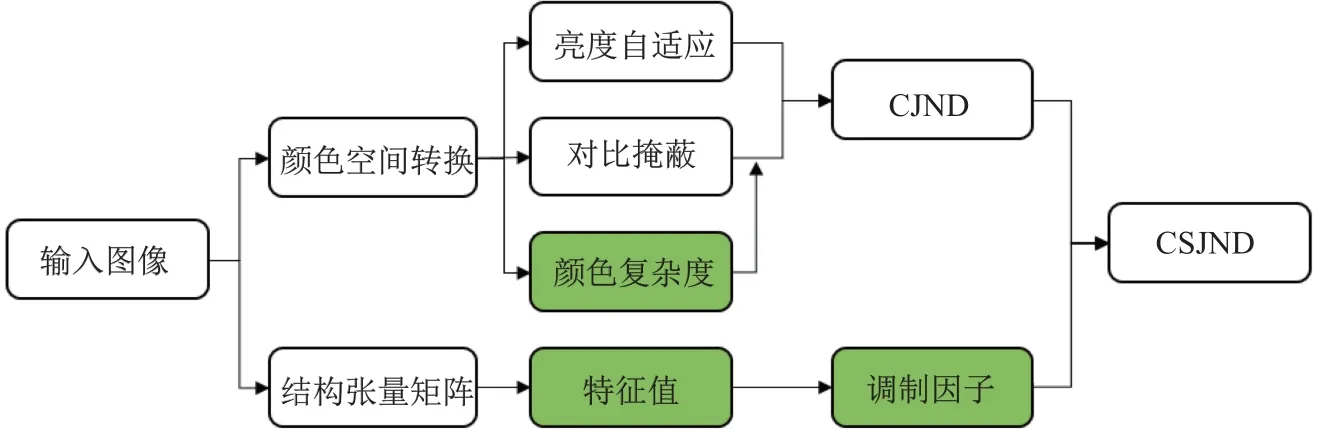
图1 本工作提出的CSJND 模型框架Fig.1 Framework of proposed CSJND model

式中: (x,y)为像素点坐标; LA 为亮度掩蔽模型; VM 为颜色复杂度调制的对比掩蔽模型;α为控制参数, 取值为0.3, 与文献[5]中保持一致.

1.1.1 颜色复杂度视觉权值

颜色是图像视觉最直观的感知特征之一, 颜色复杂度可以描述局部区域颜色的变化强度[19]. 颜色复杂度越大, 局部区域颜色的变化就越剧烈, 人眼对该区域中像素值变化的敏感度越低, 该区域对噪声的掩蔽能力也就越强[20]. 区域中颜色的变化往往也伴随着纹理的变化, 但是相比于纹理特征, 颜色特征的计算基于三通道, 保留了更多的图像信息.

颜色复杂度的计算在更加符合人类视觉感知特性的LAB 颜色空间进行[21], 利用欧氏距离来表示像素点间的差异性[22]:

式中:c(i,j)为(i,j)处的像素值;N为区域内像素点的总个数;Ω(x,y)为以像素点(x,y)为中心的邻近区域. 像素点(x,y)处的颜色复杂度为[22]

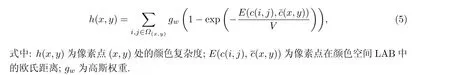
图2(a)为实验原始图像PartyScene, 颜色复杂度的计算结果如图2(b)所示. 图2(b)中, 高亮区域中的像素值比较大, 表示原图对应区域的颜色复杂度比较大. 可见, 实验输出符合预期效果, 颜色复杂度越大, 原图对应区域内颜色变化越剧烈；颜色复杂度越小, 原图对应区域内颜色变化越平缓.

图2 输入图像颜色复杂度Fig.2 Color complexity of input image

颜色复杂度能够反映出图像特征的变化. 图3 展示了输入图像颜色复杂度与模式复杂度的对比情况. 图3(a)中, 颜色从左到右逐渐变化, 亮度从上到下逐渐变暗, 纹理特征并不显著.对于具有类似特征的区域, 虽然纹理特征并不显著, 但是相关区域确实存在特征变化的情况;当只考虑单一通道上像素值的变化时(见图3(b)), 大部分区域像素值为0; 当使用颜色复杂度时(见图3(c)), 图中的像素值非0, 与原始图像的区域特征保持一致. 因此, 只考虑纹理特征并不能完全反映出各区域对噪声的掩蔽能力. 相比之下, 颜色复杂度能够反映出各个位置上的变化, 弥补了因特征不明显而导致的掩蔽作用不充分的缺陷, 进一步提升了模型的准确性.

图3 输入图像颜色复杂度与模式复杂度的对比Fig.3 Comparison between color complexity and pattern complexity of input image

颜色复杂度与视觉感受相关, 颜色变化剧烈的区域拥有较多的视觉冗余信息, 但是颜色复杂度并不能与对比掩蔽模型直接相加或相乘, 缺乏相关的理论依据, 还会导致计算得到的JND 阈值过大或过小. 为了计算颜色复杂度输出值与对应区域视觉敏感度之间的关系, 在多次实验的基础上对输出数据进行了拟合分析, 用以计算像素点(x,y)处的视觉权值Ch(x,y):

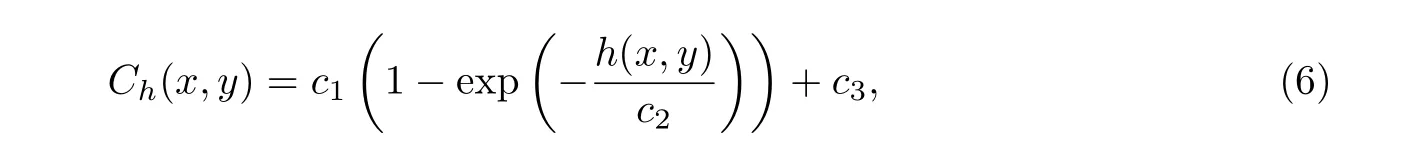
式中:h(x,y)为像素点(x,y)处的颜色复杂度;c1、c2、c3为控制参数, 通过实验结果选取主观质量最佳时的参数值, 分别取值为1.50、1.00 和0.75.

1.1.2 颜色调制的对比掩蔽模型

对比掩蔽效应是人眼视觉特性中的一个重要现象, 是指一种视觉成分在存在另一种视觉成分情况下的视觉可见性的下降[5], 是由像素的空间关系决定的, 在亮度分量上建立对比掩蔽模型:

式中:β为控制参数, 取值为0.117, 与文献[5]中保持一致;G(x,y)为像素坐标(x,y)处的最大加权平均梯度值:

式中:I(x,y)为(x,y)处的像素值;gk(i,j)为4 种不同方向的高通滤波器; gradk为梯度值.

W(x,y)为像素坐标(x,y)处的边缘加权因子, 由边缘检测图和高斯低通滤波器计算得到[5]:

式中:L为输入图像通过Canny 边缘检测器后的图像;h为高斯低通滤波器[5].

在局部区域内, 颜色复杂度越大视觉冗余信息就越多, 该区域对噪声的容忍能力也越强；反之, 则该区域对噪声的容忍能力就越弱[20]. 因此, 颜色复杂度与视觉敏感度具有很大的相关性, 可以用来衡量人眼的敏感度, 而原有的对比掩蔽模型未充分考虑颜色复杂度信息. 改进后的对比掩蔽模型记为VM(x,y):

式中: CM(x,y)为对比掩蔽模型;Ch(x,y)为基于颜色复杂度的视觉权重.

1.1.3 亮度掩蔽模型

亮度掩蔽效应是指人类视觉系统对于不同背景亮度呈现出不同的敏感度, 在较亮或较暗背景下的敏感度较低[5]. 背景亮度掩蔽模型LA 的表达式为

式中: bg(x,y)为像素点(x,y)处的平均背景亮度, 可由周围像素(5×5 邻域)的亮度值计算得到:

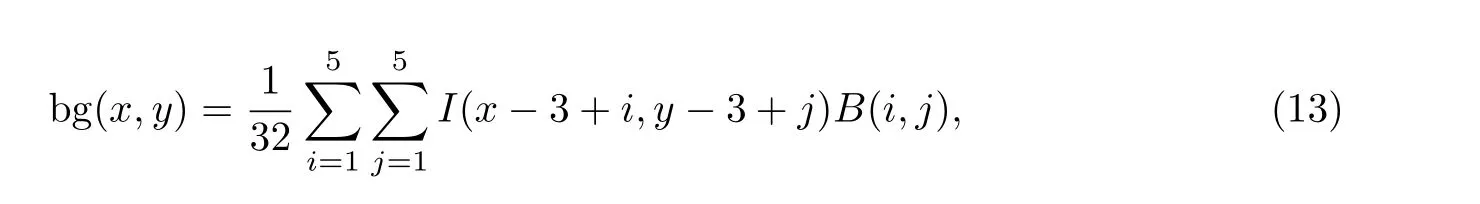
式中:I(x,y)为(x,y)处的像素值;B(x,y)为加权低通滤波器.

1.2 基于张量的结构特征调制因子

结构张量是由原来的图像梯度关系转变而来的一个新的结构关系, 并且保留了更多的结构信息, 包括像素的方向和强度[16-18], 可以利用结构张量来求取与邻域像素相关性差的点. 结构张量可以表示为如下的2×2 矩阵形式:

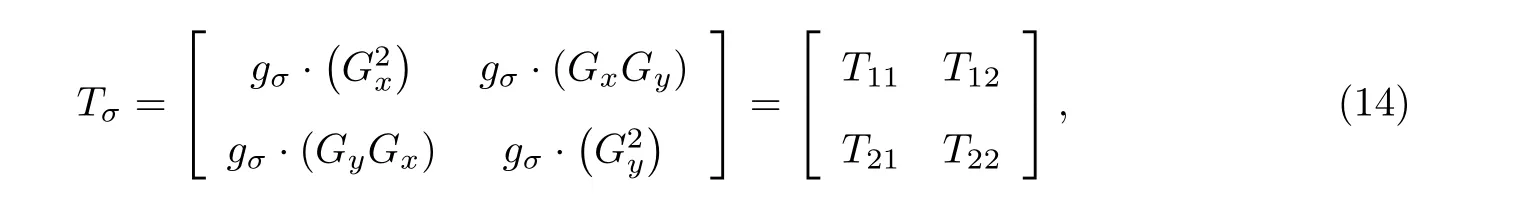
式中:gσ为高斯卷积核;Gx和Gy分别为图像在x、y方向上梯度.

对于Tσ, 计算矩阵的特征值矩阵λ1和λ2, 其大小与输入图像大小相等:

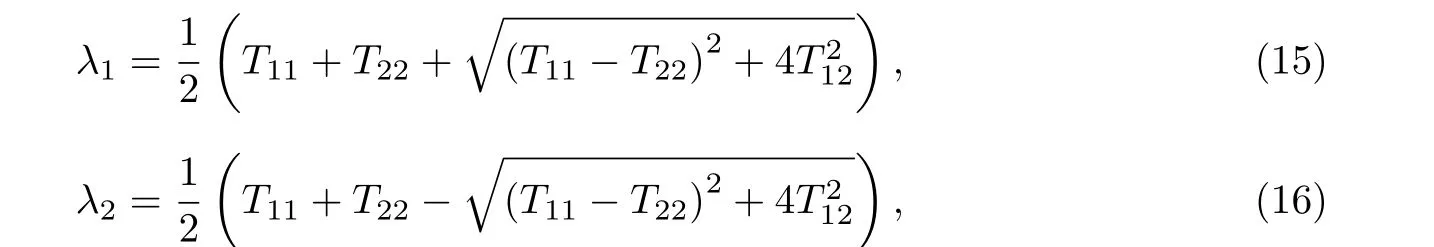
式中:Tij表示为结构张量矩阵中的元素.

对于每一个像素, 能够计算出各自的特征值λ1和λ2(λ1≥λ2), 并且满足如下性质[16]: 在平滑区域,λ1≈λ2≈0; 在边缘区域,λ1＞＞λ2≈0; 在角点区域,λ1＞＞gλ2＞＞0. 因此, 可以借助像素点对应的特征值λ1和λ2的特点, 来区分图像中的角点、边缘和平滑区域.

通过上述分析可知, 特征值矩阵λ2中元素值远大于0 的位置, 对应输入图像中的角点区域. 因此, 可以根据λ2将角点区域与其他区域进行区分. 图像中角点区域中的像素没有主导的梯度方向, 与周围像素的相关性较弱[16], 呈现出更大的无序结构特征, 可视为无序纹理区域.无序纹理区域包含更多的不确定性信息[23], 拥有较大的视觉冗余.

本工作采用特征值矩阵λ2来计算结构张量的调制因子, 如果直接使用特征值矩阵λ2, 则难以区分脉冲噪声和点状目标[24], 同时也容易产生过大的失真. 为了去除脉冲噪声的影响, 本工作进行了中值滤波操作[25]. 无序纹理区域拥有较大的视觉冗余, 人眼对该区域的像素值变化不敏感, 对噪声的容忍能力也就越强. 根据以上分析, 调制因子数值不应小于1, 计算过程如下:

式中:CT为λ2经过中值滤波后的输出结果;FST为所求的结构张量的调制因子;CT,max和CT,min分别为CT中的最大值和最小值; med{·}为中值滤波;W5×5为5×5 的滤波器.

图4 为结构张量示意图(对应式(18)中的归一化部分, 即前半部分), 反映了区域的结构特征, 图中高亮区域为角点区域, 与周围像素相关性较弱, 结构无序程度较大, 能够容忍更多的噪声. 对于平滑区域和边缘区域, 调制因子的数值较小.

图4 PartyScene 结构张量Fig.4 Structural tensor of the PartyScene

由此可见, 可以利用基于张量的结构特征来确定无序纹理区域, 像素点之间的相关性较弱, 人眼对该区域中的噪声不敏感, 而且数值的大小能够反映结构无序程度的高低, 用以去除视觉冗余.

2 性能测试

为了测试JND 模型的性能, 需要在JND 模型的引导下将噪声添加到原始图像中, 在主观感知质量相同的前提下标准峰值信噪比(peak signal to noise ratio, PSNR)值更小, 或是在PSNR 值相同的前提下主观感知质量更高, 说明该模型能够准确地计算出更多的视觉冗余, 模型性能也就更好. 噪声添加方式为

式中:F表示为输入图像; ^F表示为注入JND 噪声的输出图像;ε为噪声等级控制参数;rand(x,y)表示随机地选取+1 或-1.

2.1 掩蔽因子作用的证明

为了证明颜色复杂度、结构张量对提出模型性能的提高都有着不可忽视的贡献度, 接下来通过控制变量进行实验验证(见图5).

从图5 中可以看出, 4 幅图像的视觉主观质量相等或相近, 人眼无法察觉出它们之间的差别, 但是原始JND 模型取得最大的PSNR 值, 本模型取得最小的PSNR 值, 比前3 组分别低2.80、1.55 和1.47 dB. 只使用颜色复杂度或结构张量的JND 模型, PSNR 值相比于原始JND模型明显降低, 相比于CSJND 模型却明显增加. 实验结果证明了二者的使用有助于去除视觉冗余.

图5 颜色复杂度和结构张量的调制作用的证明Fig.5 Verification of modulation effects of color complexity and structural tensors

对于提出的JND 模型, 同时考虑颜色复杂度和结构张量这2 种因素, 在颜色变化剧烈、结构杂乱无序的区域引导更多的噪声, 噪声分配较为合理, 更加符合人类视觉系统的特点, 在保证主观感知质量的同时容忍大量噪声.

2.2 参考模型间的对比

为了进一步验证本模型的性能, 选取3 种已有的JND 模型进行对比, 分别为模型Liu2010[6]、模型Wu2013[7]和模型Wu2017[8]. 通过以上JND 模型分别向输入图像注入不同等级的噪声, 使各个受污染图像的主观感知质量尽量保持相同或相近.

在主观感知质量相同的前提下, 如果处理后的受污染图像的PSNR 值更小, 则说明该模型能够有效去除更多的视觉冗余, 相比于其他模型更加符合人眼的视觉特性. 如图6 所示, 在上述JND 模型的引导下生成4 幅失真图像. 可以看出, 这些失真图像的主观感知质量相同, 通过人眼无法察觉出差异. 但是, 在相同主观感知质量下, 本模型的失真图像取得最小的PSNR 值,比前3 种参考模型分别低1.96、1.22 和0.51 dB. 根据实验结果可以初步判断, 本模型更加符合人眼的视觉特性.

图7 为不同JND 模型在局部区域的对比情况, 图中面部区域在上, 墙壁区域在下. 图7 从图6 中选取2 个具有代表性的局部区域进行更加细致的对比, 分别是人脸区域和墙壁区域. 从人眼较为敏感的面部区域中可以看出, 各图像的主观感知质量相同, 验证了实验结果的客观性和可靠性; 图中的墙壁区域纹理结构比较规则简单, 人眼能够较容易地察觉出该区域中失真的存在: 图7(a)、(b)和(d)的主观感知质量相同, 但是图(c)中却产生人眼容易察觉的失真. 因此,本模型在主观感知质量相同, 甚至某些局部区域感知质量更好的前提下, 能获得更低的PSNR值. 实验结果证明, 本模型能够有效去除更多的视觉冗余, 更加符合人眼的视觉特征.

图7 不同JND 模型在局部区域的对比Fig.7 Comparison of different JND models on local patches

模型性能与主观感知质量密切相关. 为进一步验证本模型的性能, 选取7 幅较为经典的图像进行实验, 这些图像包括BlowingBubbles、BQSquare、BasketballDrill、BQMall、PartyScene、RaceHorses 和Newspaper, 记录下评价PSNR 和平均主观评分(mean opinion score, MOS). 本实验邀请了18 人对处理后的图像进行主观质量打分(打分范围为1～5, 分数越高表示主观质量越好), 其中12 人为图像研究者, 其余6 人没有图像研究经历. 为了保证打分结果的可靠性和可信性, 在主观打分之前这些人员都经过相关的培训过程. 打分结果如表1所示.

表1 图像质量比较Table 1 Comparison of image quality

表1 给出了客观评价指标PSNR 值和主观质量分数MOS. 从表中可以看出, 通过4 种JND 模型生成的受污染图像的主观感知质量, MOS 值均保持在4.16 以上. 相比于其他3 种模型, 本模型取得了最小的平均PSNR 值, 比模型Liu2010 低1.759 dB, 比模型Wu2013 低0.937 dB, 比模型Wu2017 低0.801 dB. 同时, 经过本模型处理的图像的主观感知质量不低于其他3 种模型, 和模型Wu2017 的平均质量分数相近, 比模型Liu2010 和Wu2013 的略高. 可见, 在主观感知质量相同或较高的前提下, 本模型的PSNR 值更低. 实验结果证明, 本模型能够更加有效地去除大量的视觉冗余信息, 更加符合人眼视觉特征.

3 结束语

本工作提出了一种基于颜色复杂度和结构张量的JND 模型, 对颜色信息和结构信息有更充分的利用. 首先, 利用颜色复杂度计算各区域中颜色变化对视觉的掩蔽效果, 使用得到的视觉权值改进对比掩蔽模型, 以提升模型的准确性; 然后, 通过NAMM 模型与亮度掩蔽模型进行叠加, 得到了基于颜色复杂度的CJND 模型. 同时, 通过结构张量矩阵和特征值计算调制因子, 计算结构不规则区域的位置和强度, 并与CJND 模型结合, 最后得到基于颜色复杂度和结构张量的CSJND 模型. 实验结果表明: 相比于其他3 种JND 模型, 本模型在主观感知质量相同的前提下PSNR 值明显降低; 本模型能够有效去除更多的视觉冗余, 更加符合人眼的视觉特征.