基于语音能量比的解决频域ICA 次序不确定性问题的算法

王志强, 王 涛, 金志文

(1. 上海大学通信与信息工程学院, 上海 200444;2. 中国人民解放军 93216 部队, 北京 100085)

盲源分离是一种在信源以及传输模型未知的情况下, 仅通过传感器采集到的混合信号来估计源信号的技术. 该技术在语音信号处理、生物医学、图像处理、机械故障诊断等方面的应用都发挥了重要作用. 尤其在语音信号处理中, 盲源分离技术为诸如语音识别等提供尽量“干净”的单一声源信号, 从而提升后端技术的性能.

盲源分离问题首次在1986 年由Jutten 等[1]提出, 在1994 年Comon[2]提出了独立成分分析(independent component analysis, ICA)的概念, 同时指出ICA 的本质和盲源分离是一样的, 由此将盲源分离的研究转化成了对ICA 代价函数的研究, 之后的大部分研究都是基于这种ICA 理论框架进行的. 早期的ICA 已经很好地解决了线性混合信号的分离, 但实际情况下语音的混合是卷积混合, 既有幅度的衰减又有时延, 而早期的线性混合ICA 不再适用于卷积混合模型, 分离性能也大大降低.

针对卷积混合信号的分离, 常见的做法是通过短时傅里叶变换将卷积问题转变为频域的乘积问题, 然后在每个频点上应用ICA 算法, 得到相应的解混矩阵对混合信号进行分离. 频域ICA 需要对每个频点单独进行ICA, 因此每个频点输出的分离信号的幅度和次序具有不确定性. 对于幅度不确定性问题, 只要能够控制每个频点的信号能量大小, 则一方面使得算法不会因为信号大小不受控制而无法收敛, 另一方面也使得各个频点的分离矩阵的数值差异较小.在这种情况下, 信号的分离性能也不会受到明显的影响[3]. 相比之下, 对分离性能影响更大的次序不确定性问题是本工作研究的重点.

目前, 针对频域ICA 的次序不确定性问题的解决算法大致可分为3 类: ①以某一声源的方位信息作为先验信息, 约束整个迭代过程[4-6]; ②根据相邻频点包络的相关性解决ICA 的次序不确定性问题[7-8]; ③根据解混矩阵的相位特征修正次序问题[9-11].

但上述算法有各自的局限, 因此本工作提出了一种新的解决次序不确定性问题的方法. 针对众多数据集、仿真混响环境和实际环境中的混合信号进行分离实验, 得到的结果均优于已有算法.

1 频域盲源分离算法

1.1 卷积混合模型

在盲源分离系统中,N个声源和M个麦克风放置在房间的不同位置, 麦克风采集到的信号为源信号以不同方式混合后得到的信号. 在实际环境中, 源信号si(t)为语音信号或噪声信号, 观测信号xj(t)则为采集到的麦克风信号. 在本工作中, 声源数和麦克风数均设置为2,即N=M=2. 此时, 源信号和观测信号可以表示为

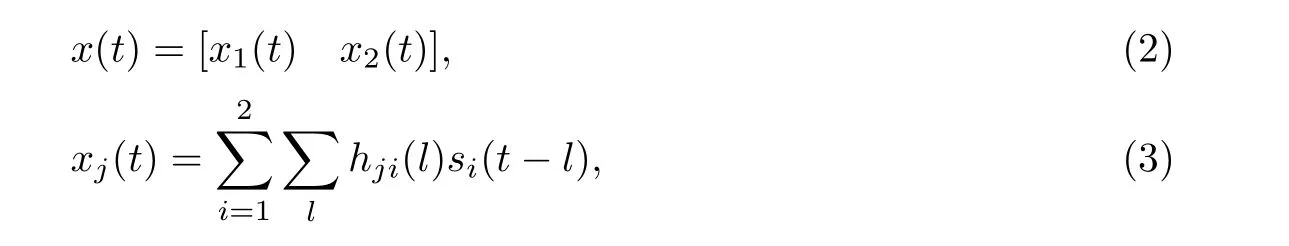
式中:hji(l)是第i个源信号到达第j个麦克风的传输函数. 此系统中, 在si(t)和hji(l)未知的情况下, 估计长为L的解混滤波器wji(l), 使得信号间尽可能独立, 从而得到分离信号yi(t),

混合系统如图1 所示.

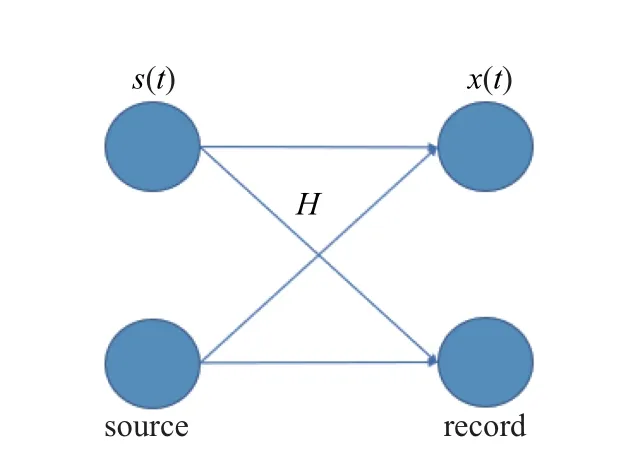
图1 混合系统Fig.1 Hybrid system

1.2 频域ICA 的实现

对式(3)的左右两端同时进行短时傅里叶变换, 可以得到其频域形式为

式中:f和τ分别为频率和帧的序号;s(f,τ)和x(f,τ)分别为源信号和观测信号经过傅里叶变换的结果; 而H(f)为在f频点上的混合矩阵, 可以表示为

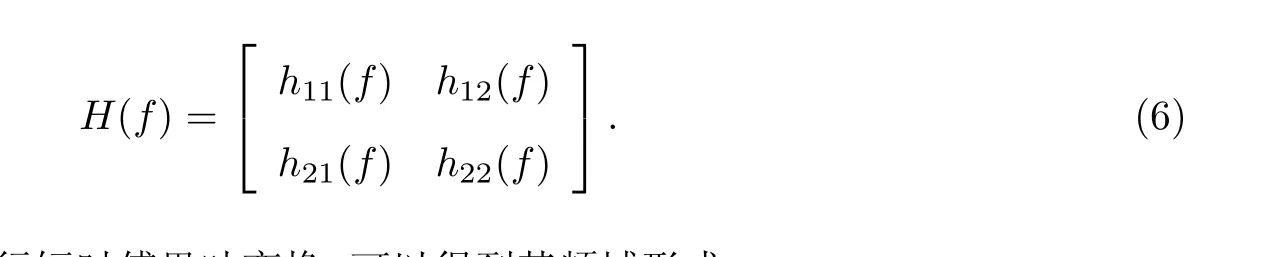
对式(4)的左右两端进行短时傅里叶变换, 可以得到其频域形式,

采用信息最大化[12]和自然梯度下降[13]的方式迭代估计解混矩阵W(f), 迭代公式为

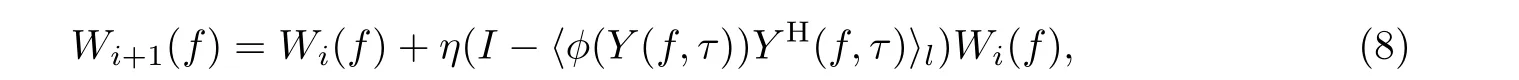
式中:η为迭代的步长;I为单位矩阵; H 表示共轭转置;〈·〉l表示对l帧求平均;φ(·)是非线性激活函数[4,6],

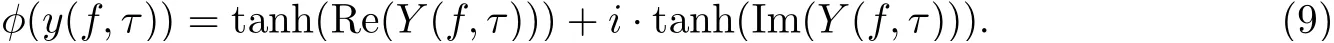
在信号的每个频点均进行迭代, 得到每个频点的W(f), 根据式(7)恢复得到分离信号. 由于分离是在各频点中独立进行的, 每一个频点迭代出来的W(f)可能是在该频点最优的, 但没有充分考虑到频点内部间的关系, 即相邻频点迭代得到的结果在包络上或在相位特征上不应有很明显的跳变.

在频域ICA 的实现过程中, 由于其每个频点独立进行迭代的特点, 不可避免地存在次序不确定性和幅度不确定性问题. 本工作采用Nesta 等[5]的算法来解决幅度不确定性问题, 着重讨论了已有的解决次序不确定性问题的算法, 并给出了新算法.

2 次序不确定性问题与已有算法

将式(7)展开可以得到

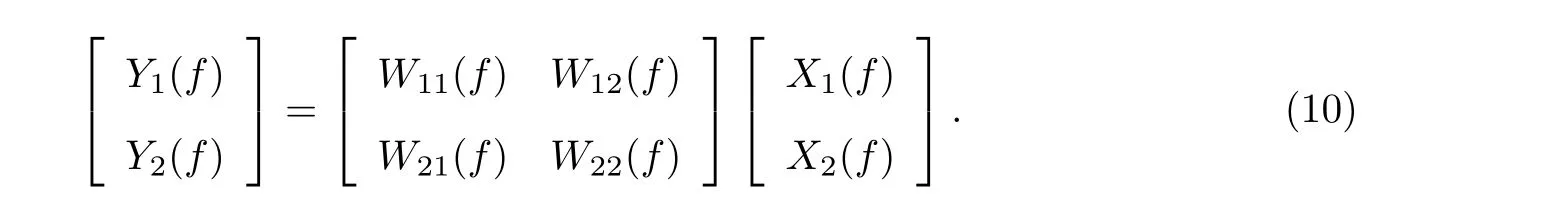
由于各频点独立迭代的特点, 会发生以下情况[9]: 当频点f=f1时, 有Y1(f1) = ^S1(f1)和Y2(f1) = ^S2(f1); 而当频点f=f2时, 有Y1(f2) = ^S2(f2)和Y2(f2) = ^S1(f2). 也就是说, 以信息最大化为准则的迭代, 对观测信号进行了有效的分离, 但是分离结果间的次序无法始终满足S1、S2这一次序, 这就导致了分离后的结果在逆傅里叶变换后, 在时域上依旧表现为未分离的情况. 如果对不同频点的ICA 之间不建立一定的联系, 那么ICA 在频率上无法保证输出的次序始终保持一致. 因此, 需要通过一定的后验信息[14]来对归属于相同源的频点进行分组, 以改善语音分离的性能.

基于频域ICA 实现语音信号盲分离的整体框图如图2 所示.

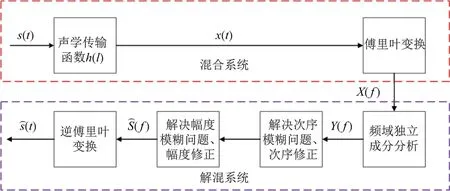
图2 基于频域ICA 的语音信号盲分离系统框图Fig.2 Diagram of speech signal blind separation system based on frequency domain ICA

2.1 到达时间差信息

通过方向信息来解决次序问题是最为常见的对分离后的频点进行聚类的方法. 式(6)中混合矩阵H(f)可以看作是若干个声源-麦克风的冲激响应, 因此可以写作

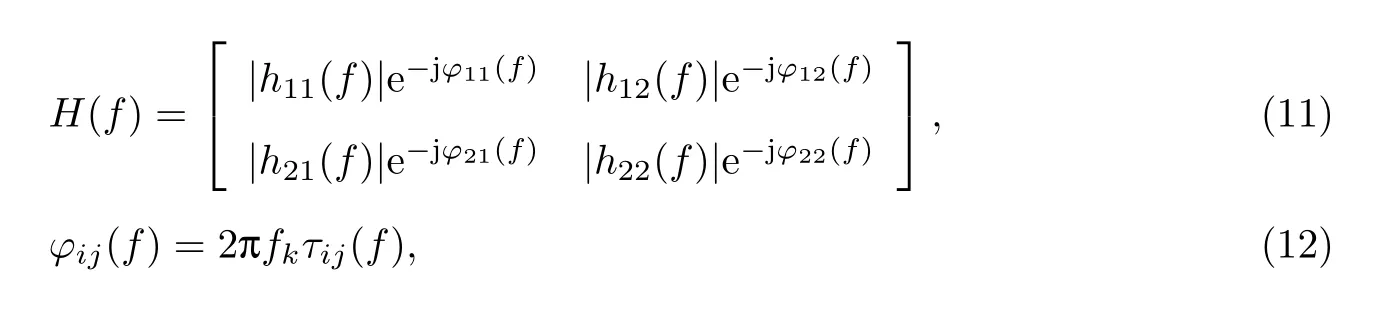
式中:|hij(f)|为第i个声源到第j个麦克风的幅频响应;fk表示真实频率;τij(f)表示对于频点f从第i个声源到第j个麦克风的时间. 观察H(f)的第一列, 可以计算出第一个声源到2 个不同麦克风的到达时间差(time difference of arrival, TDOA)信息. 对于第i个声源, 到达2 个麦克风的时延可以表示为

根据TDOA 信息可以很容易地将分离结果进行聚类, 调整后使其分离输出的顺序始终保持一致. 但同时需要设定ε=ε0, 以保证将误差在±ε之间的时延归于同一类. 但是, 该方法需要估计的TDOA 信息足够准确, 因此在分离两个同向声源或声源角度差距较小的情况下表现较差.同时, 在信号的低频成分中, 相位的差异性很小, 从而使得估计出的时延值不准确; 而在高频成分中估计TDOA 时, 会出现空间混叠问题, 这也是该方法的局限性.

本工作针对某些特殊情景中, 时延估计不准而导致次序不确定性问题无法解决的情况, 引入语音信号能量比的信息, 对次序问题进行进一步修正, 具体见第3 章.

2.2 相邻频点包络的相关性

利用相邻频点包络相关性的算法, 是根据分离后的信号中属于相同源的相邻频点间具有非常强的相关性这一特性提出的, 具体实现方式如下.

定义分离信号的包络为

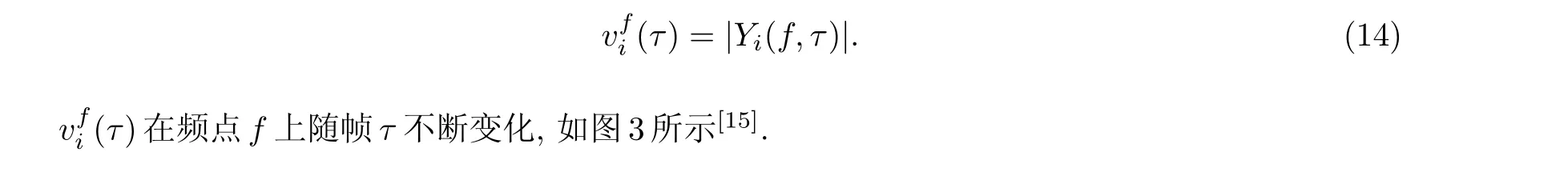
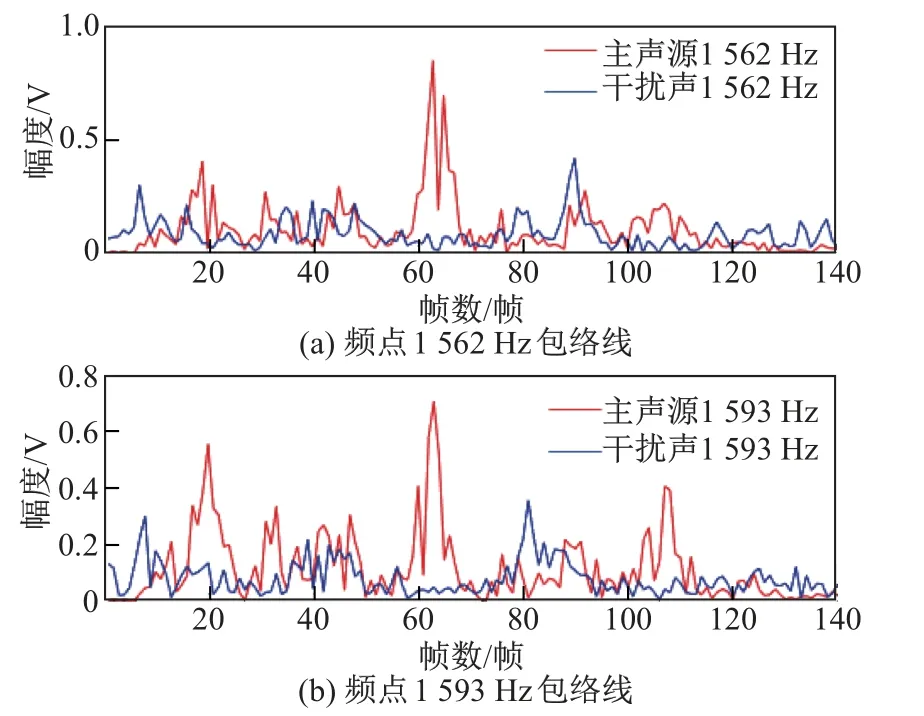
图3 不同频点上的包络线Fig.3 Envelopes at different frequencies

由于无法保证信号的每个频点包络始终满足强相关性, 因此通过递归的方式来对频点的次序进行修正会产生错误, 甚至降低分离性能.

3 基于语音能量比的次序不确定性解决算法

上述两种算法都有着各自的局限性. 首先, 利用相关性方法是不鲁棒的, 由于需要逐一对相邻频点的次序进行判断, 当在某一处频点进行误判时, 该方法会连带影响之后的所有频点,进而导致更多的频点发生误判. 其次, 利用方向信息的方法不够准确, 存在固有的无法解决同向干扰的缺陷, 同时, 其精度受到TDOA 算法的影响较大, 在低信噪比以及信号的低频和高频处, 会存在误判的情况[16-17].

本工作提出的算法是一种基于语音能量比来计算时频掩模的算法, 同时利用空间和能量的信息来对次序进行修正. 算法实现流程如图4 所示.

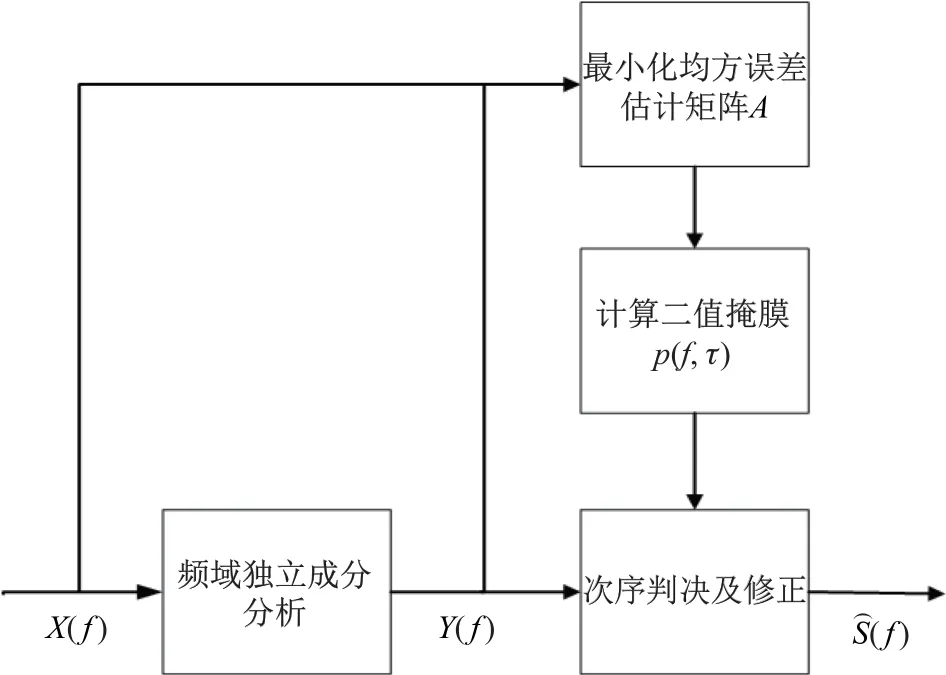
图4 次序问题修正算法框图Fig.4 Algorithm block diagram of solving permutation problem

经过ICA 算法迭代后, 可以得到分离后的信号Y1和Y2. 假设矩阵A为最小化均方误差E((X-AY)2)的结果, 可得

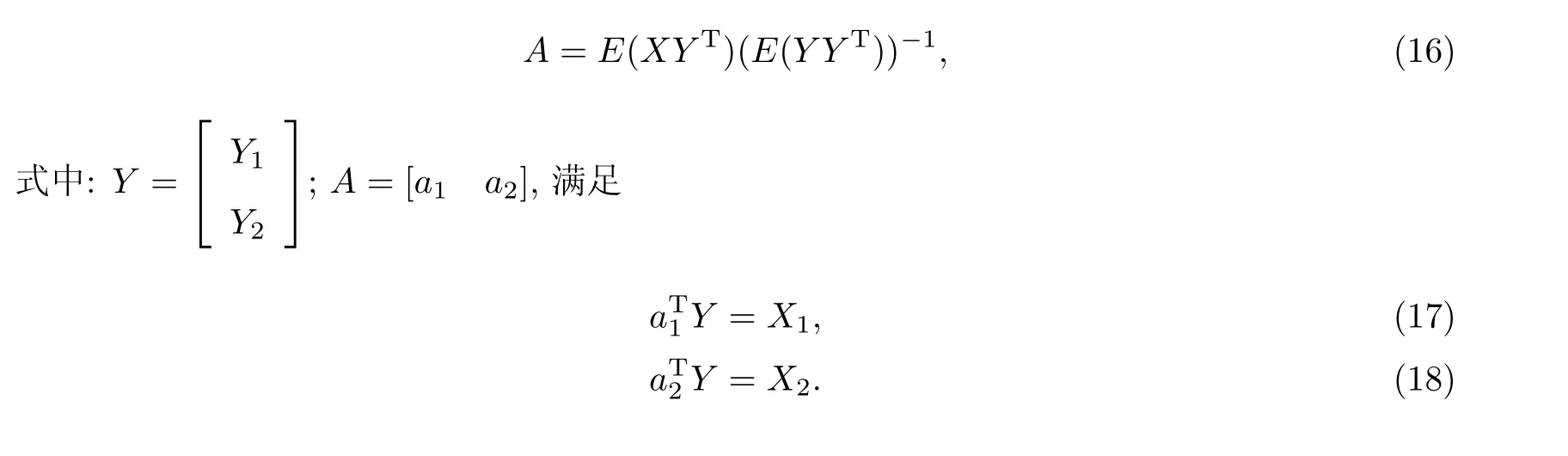
二值掩模pi(f,τ)便可以通过A计算得到

能量信息的引入有效解决了由于空间信息不准确而对次序发生误判的问题. 本工作利用空间信息对次序问题进行修正, 利用了混合矩阵H(f)的第i列应始终指向源i这一特性[6],

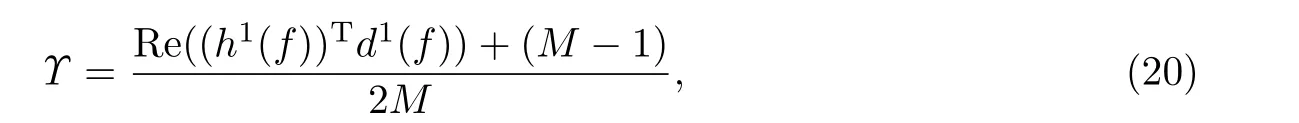
式中:h1(f)为H(f)的第一列;d1(f)为源1 的导向矢量;M为麦克风数,M= 2. 通过计算得到的pn和导向矢量dn, 定义次序问题的置信度为

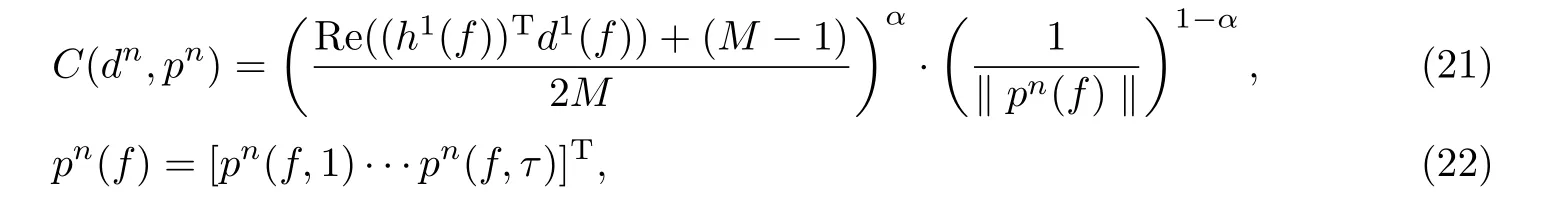
式中:α为0～1 之间的常数, 是控制方向信息和能量信息重要程度的系数. 在一般情况下,α=0.5. 当遇到同向干扰, 存在较大的混响时,α的值要适当减小.

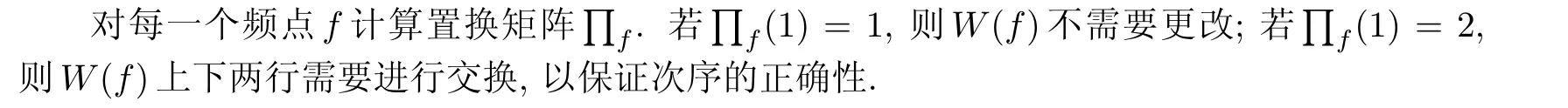
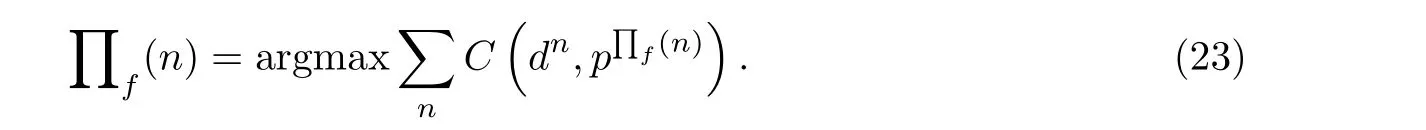
本工作提出的算法综合能量以及方向信息对次序进行判断, 能够很好地避免连带效应; 同时又针对强混响、声源同向下方向信息不准确、差异不明显的情况, 利用能量化的掩模对次序进行修正.

可以发现, 计算置信度时仅使用了H(f), 即只通过方向信息对分离信号的次序进行修正,虽然避免了连带效应的产生, 但准确性依旧受到TDOA 估计算法精度的影响, 并不能像本工作提出的算法一样, 在方向信息不准确时, 依靠语音的能量比来对次序进行准确的修正.

式(24)中通过比较|[hi(f)]HX(f,τ)|的大小来计算二值掩模, 存在一定的局限性, 即比较的是^S1和^S2的大小, 只有在声源与麦克风的距离保持不变(^X= ^S)的前提下, Nesta 等[6]的算法才是合理的. 当声源与麦克风的距离不同, 声源处幅度的比较结果并不能替代麦克风处幅度的比较结果. 在本工作提出的算法中, 使用aTi Y的比较结果来计算二值掩模更为合理, 因为矩阵A为最小化均方误差E((X-AY)2)的结果, 所以aTi Y计算的是幅度修正后麦克风处^X的结果. 通过比较麦克风处^X的大小, 才能更好地对每个频点的源归属进行判断, 这也是本工作的创新之处.

4 实验验证

4.1 实验评估标准

为了验证本工作所提出的算法的性能, 通过Vincent 等[18]定义的BSS EVAL 标准来评估算法的分离性能, 通过语音质量感知评估(perceptual evaluation of speech quality, PESQ)来评估分离后的语音质量[19].

根据BSS EVAL 标准, 分离后的信号^s可以看作

式中:s代表真实的源信号;espat、einterf、eartif分别代表空间、干扰和人为因素所带来的误差. 衡量分离性能的指标有信号偏差比(source-to-distortion ratio, SDR)、信号干扰比(source-to-interferences ratio, SDR)、系统误差比(source-to-artifacts ratio, SDR)等. 本工作使用SDR 和SIR 作为客观定量评估指标,

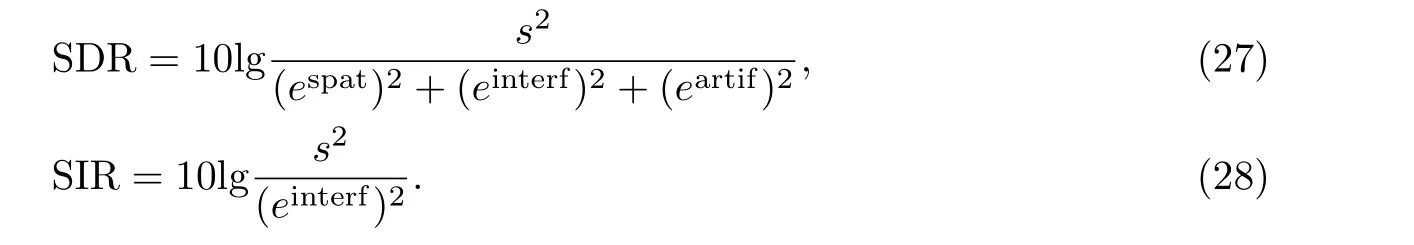
PESQ 是国际电信联盟推荐的评价语音质量的指标, 其将时域的语音信号转换为响度谱, 然后比较“干净”语音与估计语音之间的响度谱, 并给出估计信号的质量评分, 评分范围为-0.5～4.5 分.

4.2 实验1 与已有频域ICA 算法性能对比

对SiSEC2011 数据集上的语音进行分离,表1 展示了数据集中信噪比分布为-6～9 dB 数据分离后的SDR, 依次为Ozerov、Nesta 以及本工作提出算法的结果.

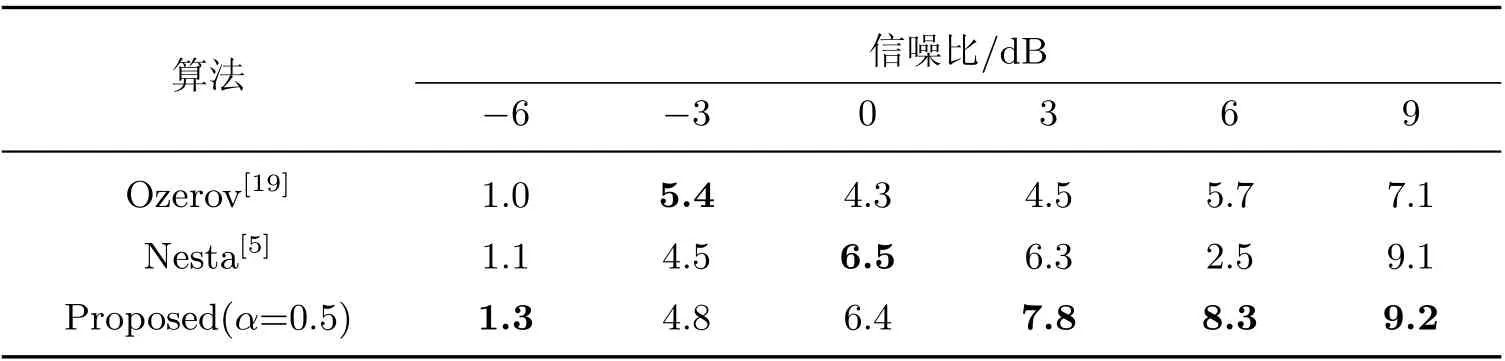
表1 SiSEC 数据集上的分离结果Table 1 Separation results in SiSEC dataset

由表1 可见: 本工作提出的算法在3～9 dB 情况下, SDR 显著优于另外两种算法; 而在-6～0 dB 情况下, SDR 与另外两种算法接近. 这是因为在恶劣的信噪比下,p1(f,τ)根据能量关系指向噪声源, 次序判决出错. 当信噪比良好时,p1(f,τ)与h1(f)共同指向主声源, 次序判决正确, 可见本工作提出的算法在分离性能的表现上更为突出.

4.3 实验2 对比频域ICA 次序问题修正的算法

在本实验中, 频域ICA 迭代算法保持相同, 仅改变次序修正算法, 来比较不同的次序修正算法对分离性能带来的提升. 数据来自CHiME1 数据集. 如图5 所示, 4 条折线分别为利用方向信息、频点包络相关性、Nesta 等[6]提出的次序修正的算法和本工作提出的算法在不同信噪比下计算得到的SIR. 图6 显示了已有算法与本工作提出的算法的PESQ 得分.α取值均为0.5.

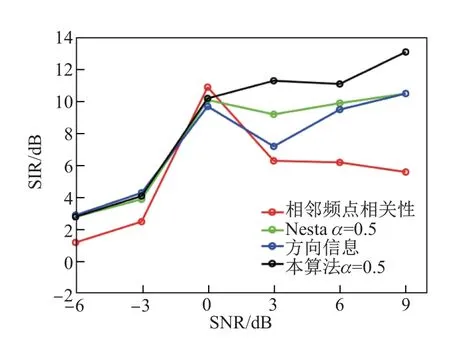
图5 4 种算法的SIRFig.5 SIR of four algorithms

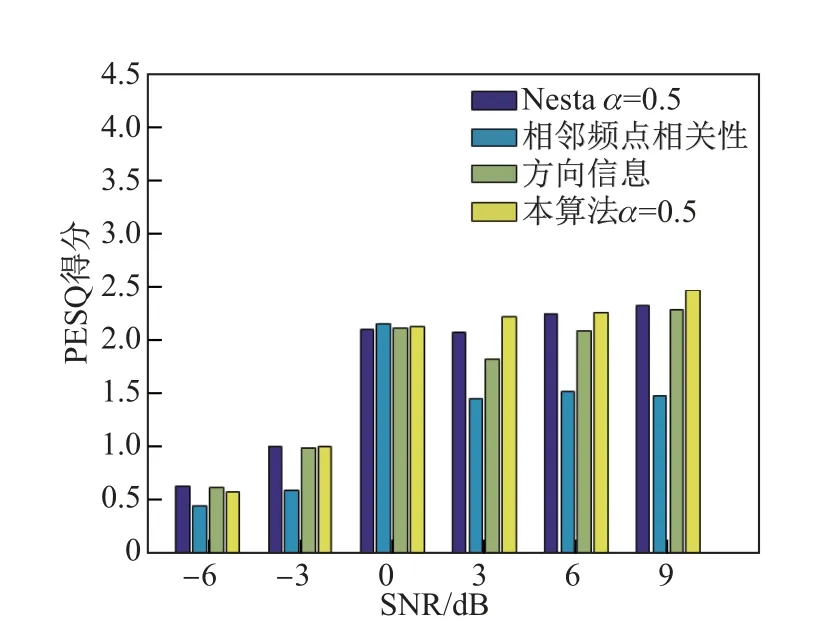
图6 4 种算法的PESQFig.6 PESQ of four algorithms

从整体上看, 本工作提出的算法优于利用方向信息或相邻频点包络相关性的算法.从SIR 表现来看, 本工作提出的算法仅在0 dB 时低于使用相邻频点包络相关性的方法;从PESQ 得分来看, 本工作提出的算法仅在0 和-6 dB 时略低于相邻频点包络相关性的方法和Nesta 等[6]的算法. 本工作提出的算法同时利用了方向和能量信息, 因此对于各个信噪比下的次序问题的判断会更加准确. 而使用相邻频点包络相关性的算法得到的SIR 变化快速是其鲁棒性不强导致的. 在0 dB 处, 相邻频点间频谱的相关性稳定, 不容易发生误判, 所以分离后的结果最优; 而在其他信噪比下, 当有一处频点发生误判, 就会连带影响到其他频点, 导致SIR 陡然下降. 从图5 可以看出, 本工作提出的算法在确保鲁棒性的前提下, 保证了次序问题判断的精度, 相比于其他算法, 显著提升了分离性能.

对比Nesta 等[6]的次序置信度公式(24), 可以发现本工作提出算法的分离性能整体上优于Nesta 算法, 可见加入能量比可显著改善分离性能. 同时在-6～0 dB 的低信噪比的情况下,Nesta 算法在分离能力上都与利用方向信息的方法保持一致; 而在高信噪比下, 性能优于利用方向信息的算法. 这是因为在高信噪比下, 迭代过程中的H(f)所指示的方向与TDOA 估计的导向矢量d(f)保持一致, 均为主声源方向; 在低信噪比下, TDOA 估计的导向矢量d(f)可能会指向噪声源方向, 与H(f)所指示的方向有较大的偏差, 影响了次序的判断, 从而分离性能下降明显.

4.4 实验3 不同α 和混响时间对算法分离性能的影响

如2.3 节所述,α是一个控制方向信息和能量信息重要程度的系数, 而α在混响情况下会极大地影响算法的分离性能. 文献[20]通过仿真的方式, 得到了声源、麦克风位置保持一致,混响时间(RT60)为0.4、0.8、1.2 s 的混合信号, 具体麦克风及声源摆放位置如图7 所示. 针对这3 个不同混响时间的混合信号, 使用不同的α进行分离, 结果如图8 所示.

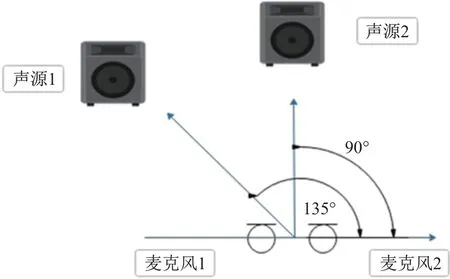
图7 麦克风及声源摆放位置Fig.7 Location of microphones and sources

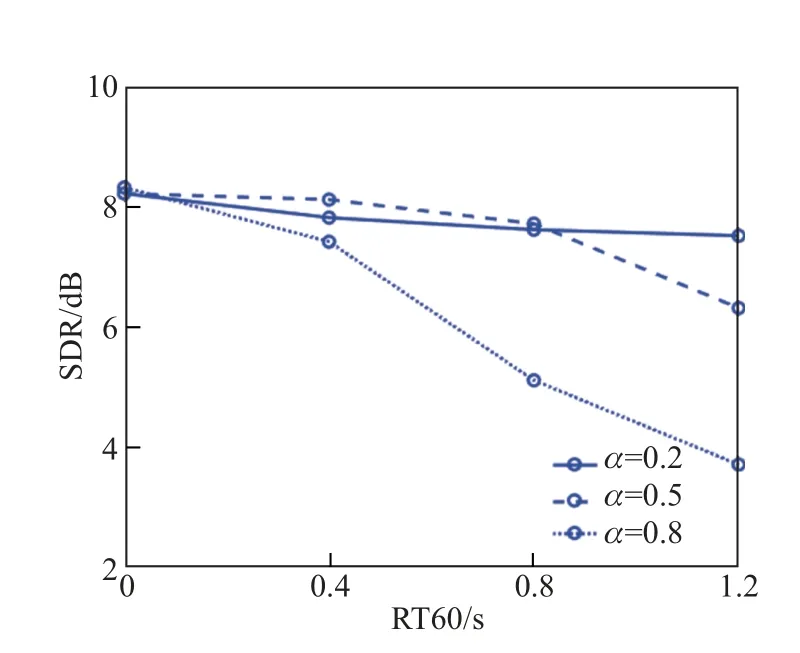
图8 不同混响时间和α 得到的SDRFig.8 SDR comparing with different RT60 and α

由图8 可见, 随着混响时间的增加, 分离的SDR 总体呈下降趋势. 在强混响的环境中, 多径效应使得估计得到的方向与真实方向有一定误差, 从而导致算法在分离性能上有一定的下降. 但正如式(20)中显示, 适当地减小α, 在次序判决中降低方向信息所占的比重, 更多地依赖能量的信息, 会使分离性能有一定提升; 但当α过小时, 只依赖能量信息对次序进行判决, 在低信噪比的情况下, 会带来分离性能的下降. 因此, 对存在强混响以及空间混叠的混合信号进行分离时, 要降低α的取值.

4.5 实验4 实际环境中混合音频的分离

为了进一步检验本工作所提算法的分离性能, 对实际环境中录制的混合音频进行了实验.实验设置如图5 所示. 房间大小为8 m×7 m×5 m, RT60=0.8 s, 2 个麦克风间距为8 cm, 声源到麦克风的距离控制在2.4 m, 且分别位于90°和135°方向. 声源2 播放“干净”的人声数据, 声源1 播放干扰声, 麦克风以16 kHz 的采样频率得到含噪语音信号. 图9 为混合信号以及分离信号的时域波形和频谱图, SDR=10.4.

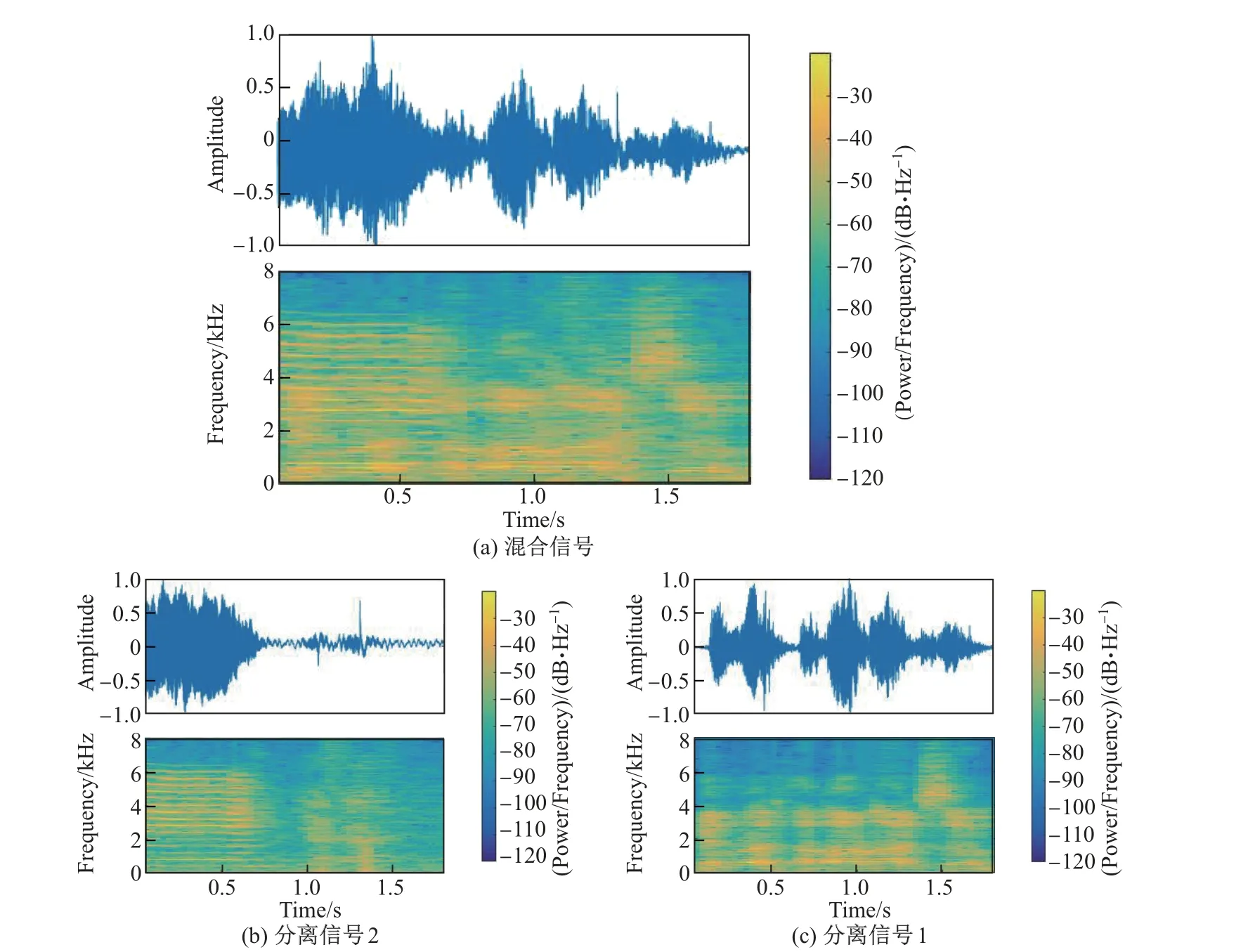
图9 混合信号以及分离信号的时域波形和频谱图Fig.9 Waveforms and spectrograms of mixed and separated signals

5 结束语

本工作提出了一种解决频域ICA 次序不确定性问题的算法, 对于SiSEC 与CHiME 数据集, 在分离性能上均比已有算法有所提升. 对已有的解决次序不确定性的若干种算法与本工作提出的算法进行了比较, 分析了各算法的优劣, 并通过实验进行了相应的说明. 同时, 在实际环境中进行了数据的采集与处理, 验证了本工作提出的算法对实际环境中的混合信号依然有着优异的分离能力. 实验结果表明, 本工作提出的基于语音信号能量比和方向性的算法有效解决了频域独立成分分析中的次序不确定性问题, 有效保护了目标语音信号, 而对干扰信号进行了有效抑制.