基于流形假设的骨架序列动作识别算法

彭亚新, 赵 倩

(上海大学理学院, 上海 200444)

人体动作识别一直是模式识别任务中最活跃的研究课题之一, 由于应用场景广泛, 众多学者都对这一课题进行了深入研究. 在过去的数十年里, 动作识别算法能够处理的数据类型已经涵盖了RGB 图像[1-2]、深度图像[3-4]以及3D 骨架数据[5-6](见图1). RGB 图像可为动作识别算法提供丰富的背景信息, 辅助判断当前人体执行的动作类别. Poppe 等[7]最先总结了基于RGB 图像的动作识别方法, 并针对动作识别领域的基本挑战提出了解决方法, 随后从图像表示和动作分类过程出发, 讨论了该领域的工作进展. Weinland 等[8]则从空域和时域的角度出发, 概述了该领域工作的处理方法. Wu 等[9]概述了基于深度学习的视频分类和捕捉任务,介绍了常用的卷积神经网络(convolutional neural network, CNN)和循环神经网络(recurrent neural network, RNN)模型的基本结构, Samitha 等[10]则讨论了常用的深度识别框架, 并对其进行定量分析. 上述工作都为输入数据的预处理带来很多启发, 其中RGB 图像容易受光线、遮挡等因素影响, 导致图像内容不清晰, 为动作识别带来了极大挑战, 这也是众多基于RGB 图像的计算机视觉任务所面临的共同难题.

与RGB 图像相比, 深度图像受光线以及照明条件的影响降低, 并且可对3D 结构信息进行编码, 例如人体的形状、边界以及整个场景的几何结构, 但是深度图像中冗余的背景信息会对动作识别产生干扰. 近年来, 基于RGB 图像和深度图像的人体姿态估计算法[11-13]日益精进, 研究人员通过提取动作的3D 骨架数据来进行动作分类. Microsoft Kinect[14]低价传感器的推出, 也使获取骨架的3D 数据更加容易.

与RGB 图像、深度图像相比, 3D骨架数据具有3 个主要特征.

(1) 空间几何信息. 3D 骨架数据记录了人体关节点的位置信息, 因此每副人体骨架都对特定时刻特定动作的空间位置关系进行了编码.

(2) 时间信息. 一个完整的动作采集的数据实际上是一个3D 骨架序列, 它是一个时间序列, 能够直观地展现骨架不同位置的先后顺序以及在时域上的相对位置.

(3) 3D 骨架序列避免了冗余背景信息的干扰. 不同于深度图像和RGB 图像中, 需要正确识别前景信息, 避免背景信息的干扰, 3D 骨架序列只存在关节点数据, 不存在背景信息.

近年来, 应用于3D 骨架序列的动作识别算法大致分为3 类: 基于概率统计的动作识别算法[1,15-16]、基于深度学习的动作识别算法[17-25]以及基于流形假设的动作识别算法[26-28].Presti 等[29]首次总结了3D 骨架序列建模以及动作识别, 阐述了3D 骨架数据的获得与预处理以及动作的表示与分类问题. Ren 等[30]则从3 个深度学习框架CNN、RNN 和图神经网络(graph neural network, GCN)出发, 介绍三者之间的差异与应用动机, 总结了基于深度学习的动作识别方法的最新进展. 上述工作是基于欧氏结构对骨架序列进行编码, 但实际上, 人的行为动作往往是分布在低维流形上的非线性规律, 因此流形能够对非线性结构和规律进行很好的描述. 通过流形假设, 可以对骨架进行合适的建模, 并且流形提供了几何计算工具, 便于对动作进行比较和度量. 因此, 本工作将对基于流形假设的动作识别算法进行概述.

1 方 法

骨架是由关节点和骨骼连接而成的铰链结构(见图2), 其中红点li(i=1,2,··· ,15)为关节点, 黑色实线ej(j= 1,2,··· ,14)为带有位置和方向的人体骨骼. 基于流形假设的骨架表示,就是对骨架结构进行建模, 将骨架从形状空间映射到流形上. 一套完整的动作对应一个骨架序列. 一个完整的骨架序列就可以看成由流形上离散点构成的轨迹(见图3). 处理流形上的动作轨迹存在一个重大挑战, 即轨迹的时间错位问题. 这会导致在对轨迹进行度量和比较时产生扭曲, 因此需要进行轨迹时间对齐. 轨迹时间对齐之后, 需要提取合适的特征来对动作序列进行进一步表征, 并将该特征作为输入数据, 输入到合适的分类器中进行动作分类. 因此, 本工作主要围绕骨架表示、轨迹时间对齐、动作序列表征和动作分类这4 个步骤来概述当前最新的工作进展, 具体框架如图4 所示.

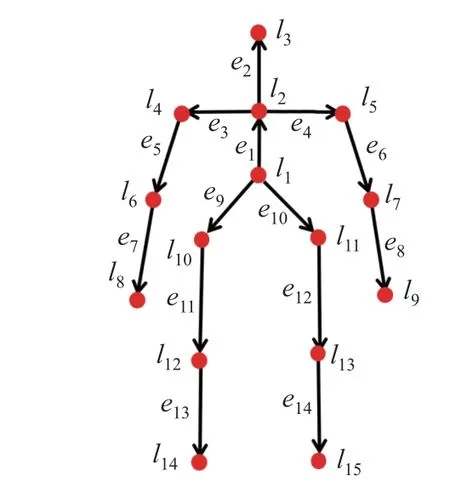
图2 骨架图Fig.2 An example skeleton

图3 将骨架序列表示为流形上的轨迹Fig.3 Representation of skeletal sequences as a trajectory in the manifold

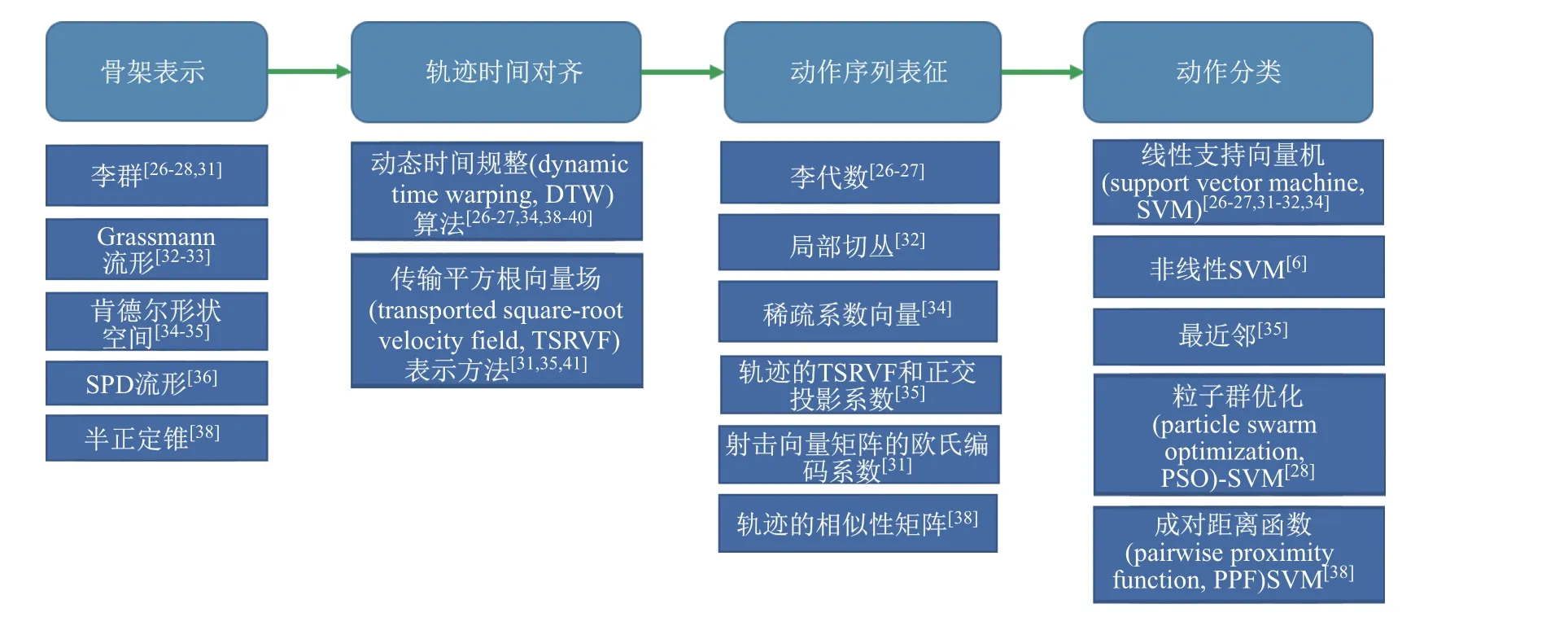
图4 基于流形假设的动作识别框架Fig.4 Action recognition framework based on manifold assumption

1.1 骨架表示

在现有工作中, 骨架常用的表示空间有矩阵李群SE(3)、Grassmann 流形、肯德尔形状空间(Kendall’s shape space)、对称正定(symmetric positive definite, SPD)矩阵流形等.

(1) 基于李群的骨架表示.

3D 骨架具有天然的铰接结构, 因此可以通过对骨骼之间的空间位置进行编码, 将3D 骨架映射到李群SE(3)上. Vemulapalli 等[26]将骨骼之间的相对位置表示成特殊欧氏群SE(3)上的一个点, 即

式中:Rm′,m(t)和dm′,m(t)是将em移动到em′位置和方向上的旋转和平移. 同理, 对骨骼em′构建局部坐标系, 可以得到骨骼em与em′在时刻t时的相对几何Pm,m′(t). 一个完整的3D骨架序列可以当成是M(M-1)个SE(3)的积空间, 即李群SE(3)×···×SE(3)上的一条轨迹, 记为

图5 骨骼em′ 在em 局部坐标系下的表示Fig.5 Representation of body part em′ in the local coordinate system of em

该工作还将每条轨迹上的离散点映射到李代数上, 即单位元处的切空间, 它等价于6 维的向量空间v= [ω1,ω2,ω3,v1,v2,v3], 由此获得轨迹的向量表示. 实验结果表明, 轨迹的李代数是一个有效的分类特征[26]. Vemulapalli 等[27]发现, 骨架的平移元素对最后分类结果的影响并不明显, 因此在骨架表示中移除了平移元素, 将骨架序列映射为特殊正交群积空间SO(3)×···×SO(3)上的轨迹, 同时提出将滚动映射与对数映射相结合, 克服对数映射在求取李代数时产生的扭曲. Xu 等[28]和Anirudh 等[31]同样选择了矩阵李群SE(3)×···×SE(3)作为骨架表示空间.

(2) 基于Grassmann 流形的骨架表示.

假设每个动作样本有T帧骨架图, 每副骨架上标记了N个关节点的位置. Slama 等[32]首先将一个动作描述为关节点3D 位置的时间序列矩阵, 即F= [p(1),p(2),··· ,p(T)], 其中p(t) = [x1(t),y1(t),z1(t),··· ,xN(t),yN(t),zN(t)]T∈R3N,t= 1,2,··· ,T是第t帧骨架图中所有关节点位置的集合, 再采用ARMA (auto-regressive moving average)模型[42]来捕捉骨架序列矩阵F的动态变化过程, 即构建线性动力系统

式中:h ∈Rd是隐藏状态向量;A ∈Rd×d是过渡矩阵;C ∈R3N×d是度量矩阵;w和u分别是服从均值为0, 协方差矩阵为R ∈R3N×3N和Q ∈Rd×d的正态分布. 该工作通过对骨架序列矩阵F进行奇异值分解(singular value decomposition, SVD), 最终求得模型参数(A,C).由于比较两个骨架序列的ARMA 模型可以转换为直接比较它们的观测矩阵, 因此作者采用有限观测矩阵(finite observability matrix)[43]:

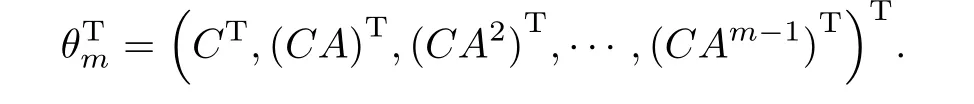
记有限观测矩阵θTm ∈R3mN×d的列向量张成的子空间为U, 该子空间恰好对应于Grassmann流形上的一个点. 骨架序列之间的相似度就可以通过Grassmann 流形上两个子空间之间的距离来度量. 假设U1和U2是Grassmann 流形G(d,D)上的两个子空间, 二者之间的测地距离为

式中:θi是主角向量, 可以通过U1TU2的SVD 分解得到.

Hong 等[33]采用了与文献[32]相同的方法, 将动作骨架序列建模为线性动力系统, 然后将线性动力系统的观测矩阵映射到Grassmann 流形上, 该项工作的目的在于数据增强. 另外, 该工作提出的VGM (variant Grassmann manifolds)方法, 将Y个动作骨架序列的子空间表示为U1,U2,··· ,UY, 对应的黎曼流形为G(d1,D),G(d2,D),··· ,G(dY,D), 其中d1到dY小于满秩子空间U的秩d. 定义从Grassmann 流形到对称矩阵空间的投影映射为

对每个子空间U, 定义α ∈{0,1}m来选择子空间的基, 那么每个动作训练样本可以得到Y个累加表示, 即

式中: 1 表示元素全为1 的向量;Gαi表示按向量αi选择该子空间上的基.

(3) 基于肯德尔形状空间的骨架表示.

Amor 等[35]将骨架序列表示成肯德尔形状空间上的轨迹. 肯德尔形状空间是一种黎曼流形, 能够表示Rd(d= 2 或3)上N个地标点的形状, 并且在不同变换下建立与形状保持相等的等价关系, 这些变换包括平移、旋转和全局缩放[44]. 在骨架表示方法中, 3D骨架的关节点就是R3上的地标点. 具体地, 令X ∈RN×d表示一副骨架形状,N为关节点数量,d为坐标维度. 为了保持形状平移不变性, Amor 等[35]采用了(N-1)×N的Helmert 半矩阵H, 用于对齐形状中心. Helmert 半矩阵H的第j行元素为(hj,··· ,hj,-jhj,0,··· ,0), 其中hj={-j(j+1)}-1/2,j=1,2,··· ,N-1. 例如, 当N=3 时,

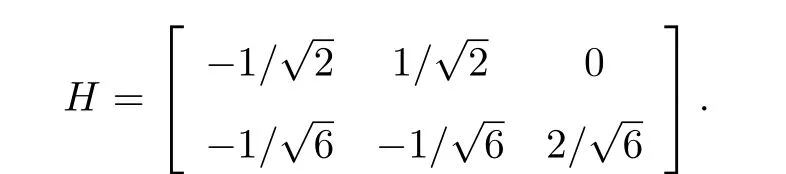
对任意X ∈RN×d,HX ∈R(N-1)×d, 形状集合记为

为了保持缩放不变性, 定义了一个预形状空间

(4) 基于SPD 流形的骨架表示.

SPD 流形也是常用的骨架表示空间. 给定一个动作样本, 有T帧骨架图, 每帧骨架图上有N个关节点. 令第t帧骨架图中所有关节点位置向量为

f(t)中共有3N个元素. Harandi 等[36]采用关节点协方差算子[37]

(5) 基于半正定锥的骨架表示.

Kacem 等[38]基于3D 关节点矩阵的Gramian 矩阵, 将骨架序列表示为半正定矩阵锥上的轨迹. 假设一个动作的骨架序列为{X0,X1,··· ,XT}, 每副骨架Xi(0 ≤i≤T)是一个秩为d(d= 2 或d= 3)的N×d矩阵,N为关节点的数量. 作者选择形状之间的成对距离矩阵作为一种形状表示. 为了便于处理, 该工作考虑距离的平方矩阵, 同时将骨架的质心平移到坐标原点. 假设li,i= 1,2,··· ,N为新坐标系下的关节点坐标,l0= (0,0)(d= 2) 或者l0=(0,0,0)(d=3)时, 成对距离矩阵D的形式为

式中:‖·‖表示L2内积〈·,·〉诱导的范数. 该成对距离矩阵D可以由N×N的Gram 矩阵计算获得. 事实上, Gram 矩阵G中的元素是点l1,l2,··· ,lN之间成对的内积:

成对距离矩阵D中的元素

因此, Gram 矩阵集合和成对距离矩阵之间可以建立线性等价关系, 从而将骨架映射到半正定锥上. 同时, Kacem 等[38]提出了Gram 矩阵之间的伪测地线计算方法, 从而将整个骨架序列表示为半正定锥上的轨迹.

1.2 轨迹时间对齐

基于流形假设的动作识别算法中, 一项重要挑战就是轨迹的时间错位问题. 通过骨架表示, 我们可以得到位于不同流形上的轨迹, 并利用流形几何计算工具来分析、度量和比较轨迹.动作的执行速率会直接影响轨迹的度量和比较结果. 所谓动作的执行速率, 就是动作完成的快慢. 例如, 两位演员执行一个相同的动作. 如果一位演员前半部分动作执行得很慢, 后半部分动作执行得很快, 而另外一位演员刚好相反, 那么即便是相同的动作, 最后采集的数据帧也会存在动作不一致的情况. 如图6 所示, 第一行动作的执行速度明显快于第二行, 导致对应帧的骨架图并不一致, 这就是时间错位问题.

图6 挥手动作骨架序列的时间错位Fig.6 Temporal misalignment of the skeletal sequences for the hand-raising action

解决时间错位问题的方法主要分为两种: DTW[45]和TSRVF 表示方法[41].

(1) 基于DTW 算法的轨迹时间对齐.

DTW 算法是一种时间鲁棒性较强的算法, 它的基本思想是基于动态规划方法, 将复杂的全局最优化问题拆分成多个局部最优问题, 该算法通过计算时间长度不同的两序列间的最优匹配路径, 来对不同序列进行时间规整. 假设一个样本动作轨迹为P={p1,p2,··· ,pS}, 待匹配的动作轨迹为Q={q1,q2,··· ,qT}, 其中S ／=T,ps(i= 1,2,··· ,S),qt(j= 1,2,··· ,T)为两个动作轨迹上的离散点. DTW 算法通过计算这两条轨迹之间的最优匹配路径, 将待匹配动作轨迹上的离散点与样本动作轨迹进行对齐. 全局匹配距离L可由

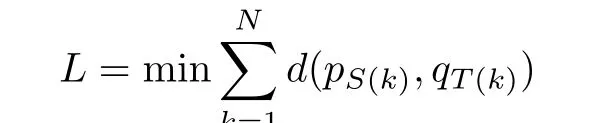
求得, 其中d(pS(k),qT(k)) 为两条动作轨迹对应离散点的匹配距离;N是匹配点对的数目.DTW 算法能够自动搜索最优匹配路径使得L最小.当二者距离小于设定的阈值δ时, 获得最终的对齐模板, 并采用DTW 算法进行最后一次对齐.

在文献[27]中, Vemulapalli 等[27]首先将骨架序列表示为李群SO(3)×···×SO(3)上的轨迹, 然后运用DTW 算法进行时间对齐. 不同于文献[26]中的方法, 作者在DTW 算法中采用了两种距离度量方式. 第一种是欧氏距离, 先将动作轨迹映射到李代数上, 然后采用文献[26]中相同的计算步骤, 获取对齐模板. 除此之外, 在文献[27]中更新对齐模板时, 并没有直接对李代数进行线性平均, 而是采用Karcher 均值算法更新对齐模板. 第二种是直接采用SO(3)上定义的测地距离

式中:R0,R1∈SO(3);‖·‖F是Frobenius 范数. 更新对齐模板时, 同样采取了Karcher 均值算法. 作者通过实验发现, DTW 算法结合SO(3)上的测地距离, 对最后的分类结果并没有显著改善.

Kacem 等[38]在半正定矩阵锥上定义了轨迹的相似性度量

式中:S+表示半正定锥;、是半正定锥上的两条轨迹;γ*(t)是最优时间规整;dS+为两条轨迹之间的伪测地距离. DTW 算法采用该相似性度量进行轨迹时间对齐.

(2) 基于TSRVF 表示的轨迹时间对齐.

Su 等[41]首次提出将TSRVF 表示方法用于轨迹的统计分析. TSRVF 的定义是一种平行移动, 即将一条光滑轨迹的缩放速度向量场平行移动到一个参考点处, 用公式表示为

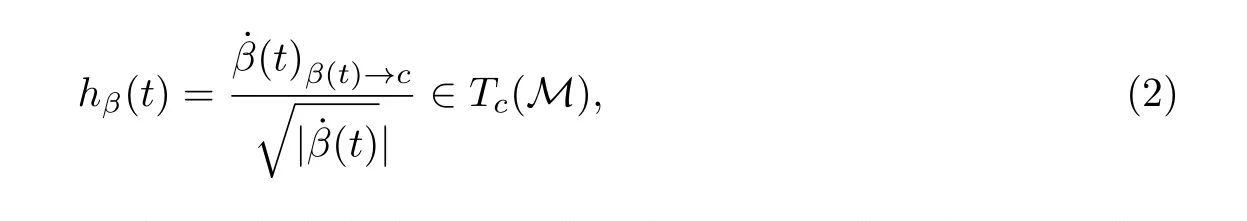
式中:β为流形上的光滑轨迹;c是流形上的参考点;M是黎曼流形;|·|是黎曼流形上的黎曼度量; 最终得到的hβ就是TSRVF. 不同轨迹的TSRVF 之间的距离定义为

式中: 距离dh是标准的L2范数, 满足对称性、正定性以及三角不等式.

假设两条流形上的光滑轨迹β1、β2,γ是时间规整,即γ:[0,1]→[0,1],γ(0)=0,γ(1)=1.轨迹对(β1,β2)和(β1°γ,β2°γ)的匹配点完全相同,但是两对轨迹之间的距离却不同.TSRVF框架对轨迹的速率不变性进行分析时, 希望得到一个在相同时间规整下, 保持距离不变的度量. 上述定义的TSRVFs 之间距离dh恰好满足这一条件, 即dh(hβ1°γ,hβ2°γ) =dh(hβ1,hβ2).此外, TSRVF 表示方法还定义了轨迹等价类之间的距离

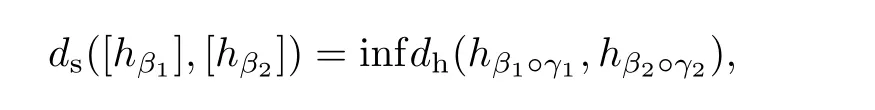
式中:γ1、γ2是不同的时间规整. TSRVF 表示方法解决轨迹的时间错位问题, 即寻找一个最优匹配γ*, 对任意δ ＞0, 使得

该目标函数可通过动态规划(dynamic programming, DP)算法进行求解.γ*最后的取值可能并不唯一, 但任意一个满足条件的γ*都可以达到最优匹配的结果.

DTW 算法在解决时间错位问题时, 采用定义在骨架表示空间上的度量, 多为欧氏距离或者相似性度量. 前者不便扩展到非欧空间, 后者并不是合适的距离度量. 因此, TSRVF 表示方法广泛应用于轨迹时间对齐. Amor 等[35]先将骨架序列表示成肯德尔形状空间的轨迹, 再根据TSRVF 的定义来对齐轨迹, 具体如下: 首先定义用于对齐的模板轨迹, 给定J条轨迹β1(t),β2(t),··· ,βJ(t),t=0,1,··· ,T, 初始化对齐模板βμ(t)=β1(t). 根据以下3 个公式更新对齐模板, 即

Anirudh 等[31]首先将骨架序列表示成李群上的轨迹, 然后采用轨迹Karcher 均值计算方法[41]得到模板轨迹. 具体如下: 给定J条轨迹β1(t),β2(t),··· ,βJ(t),t= 0,1,··· ,T; 第一步, 随机初始化Karcher 均值轨迹βμ(t) =β1(t), 计算该轨迹的TSRVF 为hβμ; 第二步, 根据式(3), 将每条动作轨迹的TSRVFhβj匹配到hβμ上, 由动态规划算法找出最优匹配γ*j, 对齐后的轨迹为～βj=βj °γ*j; 第三步, 计算对齐后轨迹的TSRVFh～βj,j=1,2,··· ,J, 并且根据

更新模板的hβμ; 第四步, 根据模板轨迹的初始条件βμ(0)=β1(0), 对

进行积分求解, 从而对模板轨迹βμ(t)进行更新, 其中c →βμ(t)表示将hβμ(t)从参考点c平行移动到βμ(t). 轨迹进行时间对齐后, 每条轨迹的TSRVF 应该与模板轨迹的TSRVF 更加接近. 因此, 整个更新过程的目标函数可以表达为

当Obj 小于给定的超参数δ时, 算法达到收敛. 最后, 根据算法第二步, 将所有动作轨迹与模板轨迹进行时间对齐.

1.3 动作序列表征

对轨迹进行时间对齐之后, 需要提取合适的特征来对动作序列进行表征. 通常用于动作序列表征的有李代数、局部切丛(local tangent bundle, LTB)、稀疏系数向量、轨迹的TSRVF 和正交投影向量、射击向量的欧氏编码系数以及轨迹的相似性矩阵.

(1) 基于李代数的动作序列表征.

Vemulapalli 等[26]将骨架序列表示为李群SE(3)×···×SE(3)上的轨迹ξ(t) = (P1,2(t),P2,1(t),··· ,PM-1,M(t),PM,M-1(t)), 为了便于分类, 将轨迹映射到李代数上. 李代数是李群单位元处的切空间, 用李代数来表征动作序列, 可以记为

式中: vec 表示将李代数用向量表示. 在任意时刻t, C(t) 是6M(M-1) 维的向量. 之后,Vemulapalli 等[27]采用李群SO(3)×···×SO(3)的李代数来表征动作序列. 与文献[26]中不同之处在于, C(t)的维度为3M(M-1), 该动作表征利用了李群上自然、有效的几何计算方法,在实验中取得了良好表现, 但仅考虑了单个动作轨迹的特征, 并没有度量不同轨迹之间的距离.

(2) 基于局部切丛的动作序列表征.

Slama 等[32]将骨架序列表示为Grassmann 流形上的点, 并提出了局部切丛的概念. 假定有N个动作类别. 作者首先采用Karcher 均值算法, 计算每类动作的平均μi,i= 1,2,··· ,N.局部切丛就是通过对数映射, 计算每个数据点映射到每个动作类别Karcher 均值点的切向量. 最后, 每个动作序列就可以用一个向量矩阵进行表征. 如图7 所示,μ1、μ2、μ3为三类动作的Karcher 均值中心,Tμ1、Tμ2、Tμ3为每类动作Karcher 均值中心的切空间; 棕色点为Grassmann 流形上的一个数据点, 黑色虚线表示从数据点映射到每类动作Karcher 均值中心的过程, 最终得到的表征结果用红、蓝、绿3 种颜色表示. 比起考虑单个数据点的切空间, 该表征更加注重比较数据点之间的距离. 然而, 对数映射在度量两个数据点之间的距离时, 可能会产生扭曲, 尤其是当两个数据点相距较远时, 会对最终提取的LTB 的有效性产生影响.

图7 动作序列的LTB表征[30]Fig.7 LTB characterization of action sequences[30]

(3) 基于稀疏系数向量的动作序列表征.

Harandi 等[36]将骨架序列映射到SPD 流形上, 并采用稀疏编码和字典学习, 找到一组动作序列的字典矩阵. 每一个动作都可以由字典矩阵与一个稀疏系数向量相乘得到.因此, 该稀疏系数向量就可以用于表征动作序列. 具体地, 在SPD 流形Sn++上, 令X={X1,X2,··· ,XN},Xi ∈Sn++为黎曼字典,φ:Sn++→H为嵌入函数. 现给定一个黎曼点x,需要寻找一个稀疏向量y ∈RN, 使得φ(X)可以由{φ(X1),φ(X2),··· ,φ(XN)}稀疏表示. 换句话说, 该稀疏表示的目标函数为

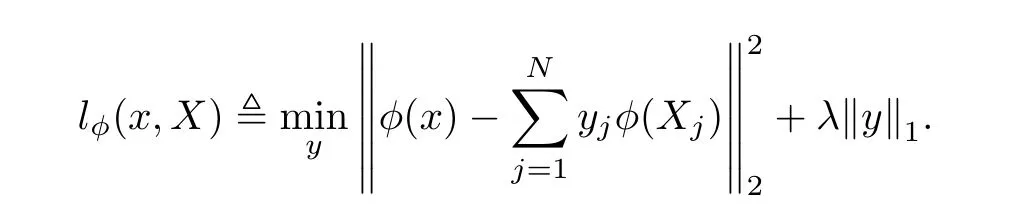
最终求解得出的稀疏向量y即可用来表征动作序列.

Tanfous 等[34]将骨架序列映射到肯德尔形状空间S中, 该工作同样采用稀疏表示和字典学习, 找到一组字典矩阵. 不同的是, 该工作通过最小化每个动作序列到所有字典矩阵元素的测地距离, 得到每个动作序列的稀疏系数向量表征. 具体地, 现有黎曼字典X={X1,X2,··· ,XN},Xi ∈S, 给定一个数据点x ∈S, 定义S上的测地距离为dS(x,Xi)=‖logxXi‖x. 因此, 目标函数为

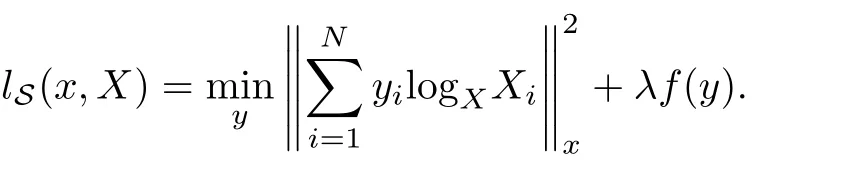
该表征采用的并不是切空间的向量表示, 而是利用稀疏编码和字典学习提取有用的信息特征,进而对动作序列进行表征.

(4) 基于轨迹的TSRVF 和正交投影向量的动作序列表征.

Amor 等[35]首先将骨架序列表示为肯德尔形状空间S上的轨迹. 由式(2)可知, 一条轨迹β(t)的TSRVF 是关于时间t的导数, 由轨迹上连续点之间的射击向量组成(见图8), 即

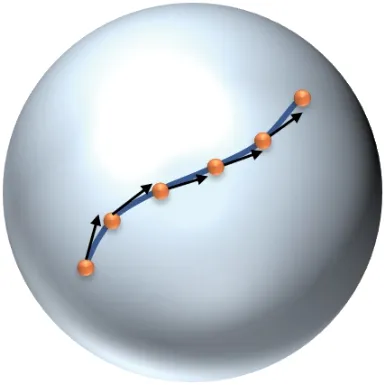
图8 轨迹上点到点的射击向量Fig.8 Point-to-point shooting vector on the trajectory

Amor 等[35]发现, 用β(t+δ),δ= 2,3,···, 代替β(t+1)可以提高最后的分类结果, 于是将筛选出的TSRVF 记为hβ,δ(t), 同时将每条动作轨迹的TSRVF 映射到一组正交基F上, 由此可以得到一组投影系数向量cβ,δ(t), 最后, 每个动作序列可以由该动作轨迹的hβ,δ(t)和cβ,δ(t)级联来进行表征. 该工作采用了两种向量特征,hβ,δ(t)考虑的是单条动作轨迹的特征, 投影系数cβ,δ(t) 则考虑轨迹之间的相互表示, 因此, 动作序列表征更加丰富.

(5) 基于射击向量矩阵的欧氏编码系数的动作序列表征.

Anirudh 等[31]将骨架序列表示为李群SE(3)×···×SE(3)上的轨迹, 并采用轨迹的Karcher 均值方法求取平均轨迹, 将每条动作轨迹与平均轨迹对齐之后, 提出采用射击向量来表征动作序列. 如图9 所示, 射击向量是切向量, 它在τ= 0 时刻从平均轨迹βμ(t)出发, 在τ= 1 时刻到达动作轨迹βi(t). 具体地, 在t时刻, 平均轨迹βμ(t)到对齐后的动作轨迹～βi(t)的射击向量为

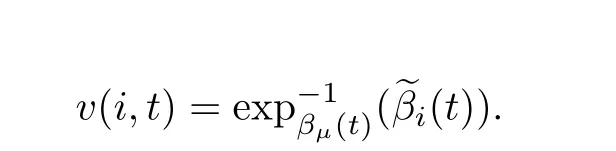
假设动作序列共有T帧骨架图, 射击向量矩阵为

此外, Anirudh 等[31]为了达到降维的目的, 采用了欧氏编码函数K: RD →Rd, 其中d ≪D.对射击向量矩阵进行欧氏编码, 最终得到[A,B] =K(V). 因此, 每个动作序列可用编码系数[A,B]表征. 该动作序列表征方法的优势在于, 如果欧氏编码函数是可逆的, 那么也可以通过最后的编码系数重构出动作轨迹.

(6) 基于轨迹相似性矩阵的动作序列表征.

Kacem 等[38]在半正定锥S+上提出伪测地线(pseudo-geodesic)的计算方式, 从而将骨架序列表示成半正定锥上的轨迹. 为了表征动作序列, 根据式(1)定义的轨迹相似性度量, 计算每条动作轨迹的相似性矩阵. 具体地, 令潜在流形上的时间参数化轨迹集合为T=βG:[0,1]→S+. 给定m条轨迹β1G,β2G,··· ,βmG, 定义两条轨迹β1G,β2G ∈T之间的相似性函数PT:T×T →R+:

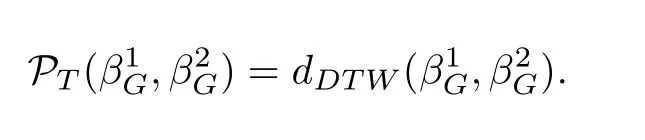
对任意一条轨迹βG ∈T, 定义映射

φ(βG)∈Rm即为轨迹的相似性矩阵, 可以用于表征动作序列, 该表征考虑了轨迹之间的比较和度量, 但缺乏对单条轨迹的特征分析.

1.4 动作分类

动作序列表征过程中提取的特征可以作为动作分类的输入数据, 选择合适的动作分类器有助于提高最终的分类结果. 目前大部分工作的分类方法都是基于SVM 的. Vemulapalli等[26-27]采用One-vs-all 线性SVM 来分类动作, 即在分类时, 选择其中某一类动作为第一类,余下所有动作为第二类, 训练一个二分类SVM. One-vs-all 线性SVM 同时训练N个二分类SVM, 其中N为动作类别数目. 同样采用线性SVM 的工作还有文献[31-32,34-36]. Wang等[6]采用非线性SVM 分类器来分类特征, 由于最终表征动作序列的是一个协方差矩阵, 故将SPD 矩阵空间常用的核函数log-Euclidean 核应用到SVM 分类器中. Xu 等[28]提出了一种PSO 算法来优化SVM. PSO 算法可以根据实际情况快速动态地平衡自适应粒子, 准确找到支持向量机的最优参数. 通过优化惩罚参数和核半径参数, 最小化SVM 误差, 从而使优化后的SVM 可以进行更好的分类. Kacem 等[38]提出了PPF SVM 用于分类特征, 该分类器的策略实际上涉及输入的构造, 即计算每条轨迹到其余所有轨迹的相似性度量, 最后将常规的SVM 应用到计算得到的数据上. 除了SVM 分类器外, 最近邻分类方法也被用于动作分类[35].

2 实验结果及分析

2.1 基准数据集

下面介绍3 个常用的动作识别数据集: Florence3D-Action 数据集[46]、UTKinect-Action数据集[47]和MSR-Action3D 数据集[48].

(1) Florence3D Action 数据集.

Florence3D Action 是2012 年在佛洛伦萨大学使用Kinect 相机采集的数据集. 它包含215 个动作序列,每个动作序列采集的帧数为8～35 帧,分别由10 位演员执行9 个动作:“wave”“drink” “answer phone” “clap” “tight lace” “sit down” “stand up” “read watch”以及“bow”.每位演员重复每个动作2 到3 次. 每帧骨架上包含15 个关节点, 展示了Florence3D 数据集中动作“bow”的部分骨架序列(见图10).

图10 Florence3D数据集中, 动作“bow”的部分骨架序列Fig.10 Part of the skeletal sequences of the action “bow” in the Florence3D Action dataset

(2) UTKinect Action 数据集.

UTKinect Action 是2012 年使用单个静态Kinect 相机采集的数据集. 它由199 个动作序列组成, 每个动作序列采集的帧数为5～74 帧, 分别由10 位演员执行10 个动作: “walk”“sit down”“stand up”“pick up”“carry”“throw”“push”“pull”“wave hands” 以及“clap hands”. 每个动作重复执行两次. 每帧骨架上包含20个关节点. 这个数据集的挑战性在于, 所有的动作序列并不是在同一视角下捕捉到的. 图11(a)和(b)虽然都是动作“walk”的骨架序列, 但是视角完全相反, 因此在处理该数据集时, 必须克服视角变换的差异.

图11 UTKinect 数据集中动作“walk”在两个视角下的部分骨架序列Fig.11 Part of the skeletal sequences of the action “walk” in the two perspectives in the UTKinect Action dataset

(3) MSR-Action3D 数据集.

MSR-Action3D 是2010 年由一个与Kinect 类似的深度传感器采集的数据集. 它包含557个动作序列, 每个动作序列采集的帧数为24～59 帧, 分别由10 位演员执行20 个动作: “high arm wave”“horizontal arm wave”“hammer”“hand catch”“forward punch”“high throw”“draw X”“draw tick”“draw circle”“hand clap”“two hand wave”“side boxing”“bend”“forward kick”“side kick”“jogging”“tennis swing”“tennis serve”“golf swing”以及“pick up and throw”. 每个动作重复执行2 到3 次. 每帧骨架上包含20 个关节点, 骨架序列从左到右, 展示了动作“high arm wave”的部分骨架序列(见图12).

图12 MSR-Action3D 数据集中动作“high arm wave”的部分骨架序列Fig.12 Part of the skeletal sequences of the action “high arm wave” in the MSR-Action3D dataset

2.2 实验结果

由表1～3 可知, 在这3 个基准数据集上, Tanfous 等[34]的工作均取得了最高的动作识别正确率, 在Florence3D Action 数据集上, 实验结果达到了94.48%, 比第二名Vemulapalli 等[27]取得的结果高出了3.08%, 比第三名Xu 等[28]取得的结果高出3.28%. 在UTKinect Action 数据集上, Tanfous 等[34]的实验结果为98.49%, 与Kacem 等[38]的实验结果相同, 并列第一. Xu等[28]的实验结果达到了97.45%, 比最优结果低1.04%. 在MSR-Action3D 数据集上, Tanfous等[34]的实验结果达到了94.19%, Xu 等[28]的实验结果达到了93.75%, 二者相差0.44%, 后者位列第二.

表1 基于流形假设的动作识别方法在Florence3D Action 数据集上的表现Table 1 Performance on Florence3D Action dataset of action recognition method based on manifold assumption

表2 基于流形假设的动作识别方法在UTKinect Action 数据集上的表现Table 2 Performance on UTKinect Action dataset of action recognition method based on manifold assumption

表3 基于流形假设的动作识别方法在MSR-Action3 数据集上的表现Table 3 Performance on MSR-Action3D dataset of action recognition method based on manifold assumption

2.3 结果分析

Tanfous 等[34]提出将骨架序列表示为肯德尔形状空间上的轨迹. 该骨架表示方法能够在刚体变换下维持骨架形状的不变性, 具有良好的鲁棒性. 此外, 由于该骨架表示直接对关节点的位置进行编码, 得到的动作轨迹保留了更多的位置信息. 该工作还采用了稀疏编码和字典学习算法, 对骨架序列的有效特征进行提取. 因此该方法在各个数据集上均取得了优异表现.

Vemulapalli 等[27]与Xu 等[28]采用的是基于李群的骨架表示. Vemulapalli 等[27]对身体骨骼之间的相对旋转进行编码, 并且提出将滚动映射与对数映射相结合, 克服了对数映射在求取李代数时易产生扭曲的问题. 滚动映射将李群上的轨迹展平, 确保当两条轨迹相近时, 它们的李代数也保持相近. 因此, 该方法最终使得表征动作序列的李代数更加有效, 分类效果更好.Xu 等[28]同时对骨骼之间的相对旋转平移进行编码, 该工作在Florence3D Action 数据集上的实验结果低于Vemulapalli 等结果的0.2%. 这是因为该工作的主要贡献在于提出粒子群优化算法来优化SVM 分类器, 从而提高动作的分类正确率, 并未对提取的动作特征进行进一步优化. 由于基于李群的骨架表示主要对身体骨骼之间的相对几何进行编码, 最后得到的动作轨迹是不可逆的, 即仅根据骨骼之间的相对几何, 无法得到关节点的位置信息. 此外, 由于相似动作的骨架会有一定程度的相像, 仅凭骨骼之间的相对位置很难进行判别, 因此, 基于李群的骨架表示对于相似动作的识别正确率通常相对较低.

Kacem 等[38]采用的是基于半正定锥的骨架表示. 该骨架表示用关节点成对距离矩阵来刻画骨架形状, 并通过Gram 矩阵来建立骨架到半正定锥的映射. 这种骨架表示方法的优势在于它同时对关节点位置的空间协方差进行编码, 对于动作幅度较大的动作, 能够得到更加精确的表征, 但在处理精细动作时, 往往识别正确率不高. 因此, 该方法在UTKinect Action数据集上取得的结果排名第一, 但在Florence3D Action 数据集上却排名第六, 它在识别动作“answering phone”时正确率仅为68.2%, “reading watch”识别正确率为73.9%.

3 基于骨架序列的动作识别算法应用

3.1 医疗康复领域

基于骨架序列的动作识别算法在医疗健康领域有着重要的研究意义. 每年全球有数百万的中风患者因运动功能下降而致残, 这严重限制了一个人日常活动的能力. 近十年来, 康复系统的发展开始帮助中风患者恢复部分运动功能. Chen 等[49]开发的中风康复系统(见图13), 其中白色球为采集动作信息的传感器. 该系统使用14 个标记点来分析和研究患者的运动, 例如,伸手和抓握, 评价指标通常是由治疗师提供的运动质量评分, 如Wolf 运动功能测试. Anirudh等[31]结合该中风康复系统, 对中风患者的运动质量进行预测. 他们采集了19 名中风患者多次重复伸展和抓握的动作, 每个动作共有14 个标记点, 并让治疗师给出每个动作的WMFT评分. 该工作将每个动作表示为李群SE(3)×···×SE(3)上的轨迹, 然后根据TSRVF 算法进行轨迹时间对齐, 并采用射击向量的欧氏系数编码进行动作表征. 最后, 将动作分类问题转化为WMFT 评分的预测问题, ground truth为治疗师给出的WMFT 评分. 实验结果与真实WMFT 评分的相关度最高达到了97.84%. 这项工作可以协助医生对中风患者的康复状况进行评估, 具有重大的医疗意义.

图13 中风康复系统[49]Fig.13 Stroke rehabilitation system[49]

3.2 监控安全领域

防护监控是动作识别算法的另一应用领域. 随着家用摄像头的普及, 人们可以用它对家中老人、小孩的行为活动进行监控, 一旦发生意外, 及时预警. 如图14 所示, 摄像头捕捉人物的摔倒动作[50], 然后在人体姿态估计模型[13]的帮助下, 将采集的视频数据分割为单独的帧, 并对每帧中的人物提取关节点信息, 在2D 或3D 上形成一副骨架, 从而得到摔倒动作的骨架序列.之后进一步采用基于骨架序列的动作识别算法对当前动作进行识别, 一旦判定为摔倒等危险动作, 及时发出预警通知家人.

图14 对摔倒动作的RGB 图像序列提取骨架序列Fig.14 Extract the skeletal sequences from the RGB image sequence of the fall action

安全监控也是银行、酒店、出租车内等社会公共场景防范暴力犯罪的重要手段. 通过监控摄像头, 可以实现人体目标的追踪以及动作数据的采集, 然后利用动作识别技术, 对目标的行为动作进行识别与预测. 当目标出现击打等暴力行为时, 可以立即通知安保人员并报警. 动作识别技术能够起到重要的防范作用, 因此在监控安全领域有着重大的研究意义.

3.3 其他应用领域

相似的应用场景还有健身App 的使用. 当用户使用健身App 时, 摄像头会捕捉并记录用户在运动过程中的动作, 通过人体姿态估计模型提取出骨架序列后; 再采用流形假设等方法对骨架序列进行分析, 找出健身练习动作中的错误; 最后将对错误动作的描述以及改进建议反馈给用户.

动作识别技术还可应用于行人再识别任务. 通过采集不同目标的行为动作, 可以构建目标与步态数据的一对一映射. 然后利用动作识别技术, 刻画不同目标步态之间的差异, 实现不同目标的步态分类, 最后由一对一映射达到行人再识别的目的.

4 结束语

流形可以很好地描述非线性结构和规律. 本工作从动作识别框架的4 个步骤着手, 对基于流形假设的动作识别方法进行了回顾与分析. 据我们所知, 这是第一篇从流形假设的角度出发, 对基于骨架序列的动作识别方法进行探讨的工作. 在这类方法中, 通过流形假设, 能够对骨架数据的空间几何信息进行编码, 将动作的骨架序列表示为流形上的一条轨迹或者一个数据点. 骨架序列之间的时序关系处理也是一大挑战. 针对动作轨迹存在的时间错位问题, 多项工作采用了DTW 算法和SRVF 表示两种方法进行处理. 同时, 流形上的几何计算工具为分析和度量动作轨迹提供了便利. 在动作表征时, 除了考虑单条动作轨迹的特征分析, 还需要从全局层面度量轨迹之间的相似性, 提取轨迹间的信息特征. 最后, 文章对当前常用的动作分类器进行了概述.

纵观发展现状, 动作识别框架的每个步骤都存在优化的潜能, 因此我们对以下5 点进行展望. (1) 更加有效、鲁棒的骨架表示仍是一个可研究的方向. 当前的骨架表示方法都有适用的数据集, 当两个数据集分布差异大时, 直接采用已有的骨架表示方法, 可能无法取得良好的动作识别结果. 因此, 可以考虑将域迁移引入到骨架表示中, 构建一个更加有效、鲁棒的骨架表示框架. (2) 针对轨迹的时间错位问题, DTW 算法需要结合流形上合适的距离度量, TSRVF表示则需要轨迹上的每个离散点均可导. 这两类方法在进行时间对齐时, 都需要找到一条合适的对齐模板. 这个模板通常是向量空间的线性平均向量, 或者是流形上通过Karcher 均值算法计算得到的平均轨迹. 然而, 在向量空间进行时间对齐时, 特征已经失去了骨架结构的非欧信息. Karcher 均值算法在寻找平均轨迹时, 需要初始化对齐模板, 最后得到的平均轨迹事实上依赖于初始值的选择. 因此, 在进行轨迹对齐时, 寻找一个无偏的对齐模板仍是一个值得研究的问题. (3) 在动作表征阶段, 除了对流形几何工具的运用, 更需要考虑如何提取轨迹以及轨迹间相互关系的特征. (4) 动作分类器的选择是当前可做研究最多的地方. 目前, 大多数基于流形假设的动作识别方法, 采用的是基于SVM 的分类器, 少数工作中采用了最近邻分类法. 由于动作序列最后都由一个矩阵或一个向量表征, 因此可以考虑度量学习等更加鲁棒的分类方法来进行动作分类. (5) 从应用的角度出发, 动作识别算法还可应用于病患的步态分析. 通过采集患者进行复健时的动作序列, 分析当前患者的康复程度, 从而帮助医生制定患者下一阶段的复健疗程.