重质油稳定性的耗散粒子动力学模拟

2022-11-13关冬张霖宙赵锁奇徐春明

化工学报 2022年10期

关冬，张霖宙，赵锁奇，徐春明

（中国石油大学（北京）重质油国家重点实验室，北京 102249）

引言

重质油在开采、储运及加工过程中常因体系的稳定性下降而带来一系列问题。重质油稳定性判定及预测对重质油加工过程具有重要指导意义[1]。传统的重质油稳定性判定法依赖于实际经验，如Stankiewicz 等[2]根据现场经验与实验观察，将沥青质与胶质的比值（asphaltene∕resin）及饱和分与芳香分的比值（saturate∕aromatic）作为判断重质油稳定性的依据。胶体不稳定指数（C.I.I.）则将沥青质与饱和分的加和（asphaltene+ saturate）同芳香分与胶质的加和（aromatic+ resin）的比值关系作为判断重质油稳定性的依据[3-5]。上述经验方法形式简单，但存在一定的局限性，如重质油四组分（saturate aromatic resin and asphaltene，SARA）间比例关系不唯一。因此，进一步从理论层面分析，建立基于分子层次信息的重质油稳定性计算方法对于认识其化学本质和工业应用十分重要。

导致重质油稳定性下降的原因是重质油胶体分散体系被破坏，更深一层次的原因是沥青质的聚沉。因此，研究沥青质的微观聚集态，得到重油分子微观聚集模型，有助于从分子层面揭示重质油稳定性下降的原因。早在20 世纪60 年代，研究者对沥青质的微观聚集态就有了一定的认识。其中，Yen[6-8]提出了经典的沥青质聚集体模型。Mullins[9-11]在Yen 模型的基础上进一步提出了Yen-Mullins 模型，成为目前最受认可的沥青质聚集模型。Yen-Mullins 模型认为，沥青质分子形成最终聚集体的过程中，将经历纳米聚集体（nanoaggregate）和团簇（cluster）两个聚集层次。当沥青质浓度很低时，为单体分散状态；随着沥青质浓度的增大，聚集数量增大，最终形成絮凝沉淀[9,12]。除此之外，很多学者对沥青质聚集结构进行了定量表征[13]。Andreatta 等[14]用超声波将沥青质分散于甲苯溶液中，发现1 个纳米聚集体约由5 个分子所构成，这与VPO 测量的相对摩尔质量一致。Indo 等[15]采用离心分离法，测量了沥青质分子纳米聚集体的直径约为2 nm。同时，他们还发现纳米聚集体通常由3～8 个沥青质分子组成。Durand 等[16]采用1H 核磁共振扩散序谱（1H nuclear magnetic resonance diffusionordered spectroscopy，1H NMR DOSY）分析沥青质纳米聚集体时发现，纳米聚集体的平均摩尔质量为6900 g∕mol，且主要分布在1500～8500 g∕mol 之间，其平均半径约为1.56 nm。以上研究对沥青质微观聚集态给出了定性聚集构型与定量聚集体结构的描述。然而，重质油体系十分复杂，难以从实验角度直接观测到重质油的微观聚集体结构。因此，研究人员试图采用分子模拟技术得到重油体系的微观聚集结构[17]。 Headen 等[18]利用分子动力学（molecular dynamics，MD）模拟得到了平衡状态下沥青质在甲苯中的有序聚集结构，即纳米聚集体结构。Frigerio[19-20]基于MD 模拟再现了沥青质分子在不同溶剂中的微观聚集态。然而，受限于MD 方法的模拟尺度，不少学者尝试基于介观尺度分子模拟方法得到重质油体系微观状态。Wang 等[21]基于粗粒化分子动力学方法再现了重质油中沥青质在甲苯和正庚烷溶剂中的自组装行为。Aguilera-Mercado 等[22]基于Monte Carlo（MC）法在介观水平上建立了原油中沥青质和胶质聚集的分子模型。相比于以上方法，耗散粒子动力学（dissipative particle dynamics，DPD）方法模拟尺度更大，且更适用于复杂胶体体系建模，将其应用于重质油体系尤为适宜。张胜飞等[23-30]经过多年研究，在DPD 模拟过程中引入刚体转动算法，系统探究了重质油的微观胶体结构与聚集行为。基于DPD 模拟结果，张胜飞等[29]认为沥青质与胶质的比例存在一个极限，当大于这个极限时，重质油将出现聚沉。Ruiz-Morales等[31]采用不同于张胜飞等的建模方法，通过加大DPD 珠子间的弹性常数并限制其键长的方式，得到了沥青质分子的刚性结构，研究了沥青质分子在油水界面的择优取向问题。此外，Rezaei 等[32]和Alvarez 等[33]对沥青质分子按基团功能划分，研究了沥青质对油水乳状液体系的影响。课题组前期工作中[34]建立了SU-DPD 框架，规范化了石油体系粗粒化建模方法并用于重质油体系，模拟结果符合理论与实验规律，证明了SU-DPD框架的准确性。

以上研究结果表明，基于DPD 方法可以准确计算重质油的微观聚集结构，为重质油稳定性的判断提供基础。本文基于SU-DPD 框架，建立四组分含量不同重质油体系，计算重质油体系的微观聚集态，统计沥青质的聚集率以判断重质油的稳定性。将沥青质聚集率与C.I.I.指数及稳定性判定图对比，以证明模拟体系的准确性，并讨论C.I.I.指数及稳定性判定图的局限性。基于DPD 模拟结果提出改进的重质油稳定性判定图，为实际重油加工过程提供指导。

1 模拟方法

1.1 DPD基本理论

耗散粒子动力学方法最先由Hoogerbrugge等[35-36]提出，最初应用于复杂流体力学领域，是一种全新的基于粗粒化粒子之间软相互作用的介观尺度模拟方法。随后，Kong 等[37]在耗散粒子动力学模拟体系中引入珠子-弹簧模型，使耗散粒子动力学方法可以模拟大分子体系。Español 等[38-39]关联了DPD 中随机力与耗散力的权函数，证明了两者之间必须满足涨落-耗散定理，夯实了DPD 的理论基础。Groot 等[40]证明了保守力参数与Flory-Huggins 参数之间存在对应关系，为保守力参数的计算提供理论依据。至此，耗散粒子动力学方法已经具备了一定的理论基础，可以用于模拟如重质油这样的复杂体系。

传统耗散粒子动力学方法为了简化计算采用无量纲单位制，模拟的基本结构单位称作DPD 珠子，DPD 珠子与分子结构一一对应[35-36]。通过规定珠子的单位质量、单位长度和单位能量可以计算体系中的所有物理量。随着计算机计算能力的加强，如今可以采用真实单位制以达到更高的模拟精度。耗散粒子动力学方法力场形式相对简单，每个珠子所受合力由5个分力组成，包括保守力、耗散力和随机力三种非成键力以及弹性力和角作用力两种成键力[35-36,40]：

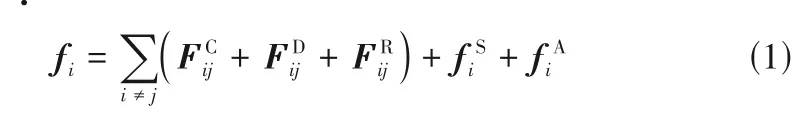
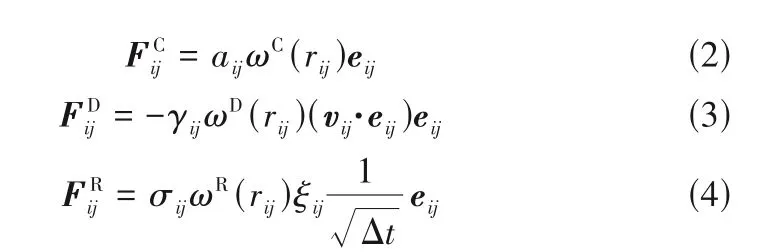
其中，aij为保守力参数；γij为耗散力参数；σij为随机力参数；eij为单位向量；ξij=ξji为平均数为0、方差为1 的随机数。随机力与耗散力可以通过随机-耗散定理关联，如式（5）和式（6）所示，两者动态平衡以达到对体系控温的目的[40]。

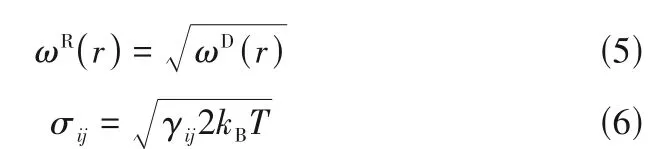
其中，kB为Boltzmann 常数。一旦温度T和γij确定了之后，σ随即确定。研究结果表明，在无量纲单位下，γij= 4.5 往往可以获得精确的模拟结果，其值的改变对模拟结果影响不大[38-40]。

DPD 模拟过程中最重要的参数为保守力参数，保守力参数可由Flory-Huggins 参数关联得到。当体系密度接近1 g∕cm3时可以采用式（7）计算保守力参数：

其中，aAB代表A 珠子与B 珠子之间的保守力参数。Flory-Huggins 参数χ可由溶解度系数求得，如式（8）所示。

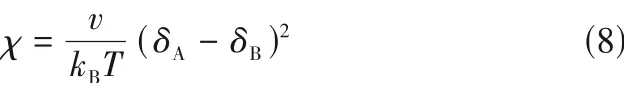
其中，δA和δB分别为A 珠子和B 珠子的溶解度参数；v为珠子的平均体积。可以看出DPD 模拟体系中除保守力参数外，其余参数均可直接确定，保守力参数及体系的粗粒化方法的确定是DPD 方法准确性的关键所在。

1.2 SU-DPD框架

为了能准确模拟重质油体系，课题组前期在传统DPD 模拟框架下，提出了SU-DPD 框架[34]，用于石油体系粗粒化分子建模及模拟参数计算，本文仅做简要介绍。SU-DPD 方法中对分子的粗粒化方法提出了完整构建规范，其构建思想源自结构导向集总（structure-oriented lumping，SOL）法[41-42]。在此基础上，本课题组对SOL 法进行了修改和补充，提出了结构单元耦合键电矩阵（structural unit and bondelectron matrix，SU-BEM）法，实现对石油中的复杂分子的准确描述，SU-DPD 法继承了SU-BEM 方法中分子的划分方法[43]。SU-DPD 方法中共定义了3类珠子，即烃类珠子、杂原子珠子和溶剂珠子，如图1（a）所示，不同的字母代表结构不同的珠子。N 类和R 类珠子中碳原子以碳碳单键相连，N2～N6 珠子用于组成环烷环结构，R2 和R3 珠子用于组成烷基侧链结构，数字的大小代表碳原子的个数。杂原子片段珠子S、NI5、NI6 和O 珠子分别对应噻吩、吡咯、吡啶和苯酚环状分子片段。溶剂珠子中T为甲苯珠子，W 为水珠子，其中一个甲苯分子划分为一个T珠子，三个水分子划分为一个W 珠子。随着模拟体系的不同，SU-DPD 方法中珠子的数目可以进一步扩充。

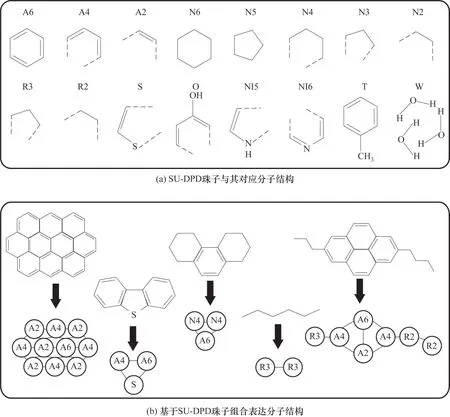
图1 SU-DPD珠子与分子表达示意图Fig.1 Schematic diagram of SU-DPD beads and molecular expression

基于SU-DPD 珠子的分子粗粒化过程示意图如图1（b）所示。粗粒化过程从稠合芳香环结构开始，锁定A6 珠子后，在其周围间隔地划分A4 与A2 珠子，以此类推。随后加入环烷环系珠子，连接方法与稠合芳香环珠子一致。对于链状分子或者烷基侧链，每3个相邻碳原子划分入1个R3珠子，划分完所有R3 珠子之后若剩余2 个碳原子则划分为R2 珠子。对于含杂原子分子片段，需要在划分稠合芳香环及环烷环时一并划分。

SU-DPD 框架中珠子间保守力参数采用关联Flory-Huggins 参数获得。基于DPD 珠子所对应的分子结构可以采用分子动力学模拟计算其平衡构型，进而统计其溶解度参数，得到每个珠子的溶解度参数后可以计算两两珠子间的Flory-Huggins 参数χ，进而计算两两珠子间的保守力参数，如式（7）、式（8）所示[34]。珠子之间的保守力参数如表1 所示。区别于传统无量纲DPD 方法，本文采用真实单位DPD 方法，即不同的珠子具有不同的质量与体积，珠子的质量和体积与所对应的结构片段保持一致。模拟过程中的截断半径以水珠子为基准，取6.46 Å（1 Å=0.1 nm），与文献报道的参数设置一致，且水珠子半径介于所有SU-DPD 珠子之间，较为适宜用作截断半径基准[21-28]。耗散力参数取0.08854 amu∕fs。模拟体系采用NVT 系综，盒子的边长一般大于10 nm，分子填入量一般大于10000 个。为保持稠合芳香环系的刚性特征，粗粒化珠子之间弹性链的弹簧常数取300 kcal∕(mol·Å2)（1 cal=4.18 J），平衡距离为3 Å[44]。具体模拟步骤为：（1）体系能量最小化；（2）NVT 系综模拟；（3）在步骤（2）的最终结构基础上进行NVT系综模拟。

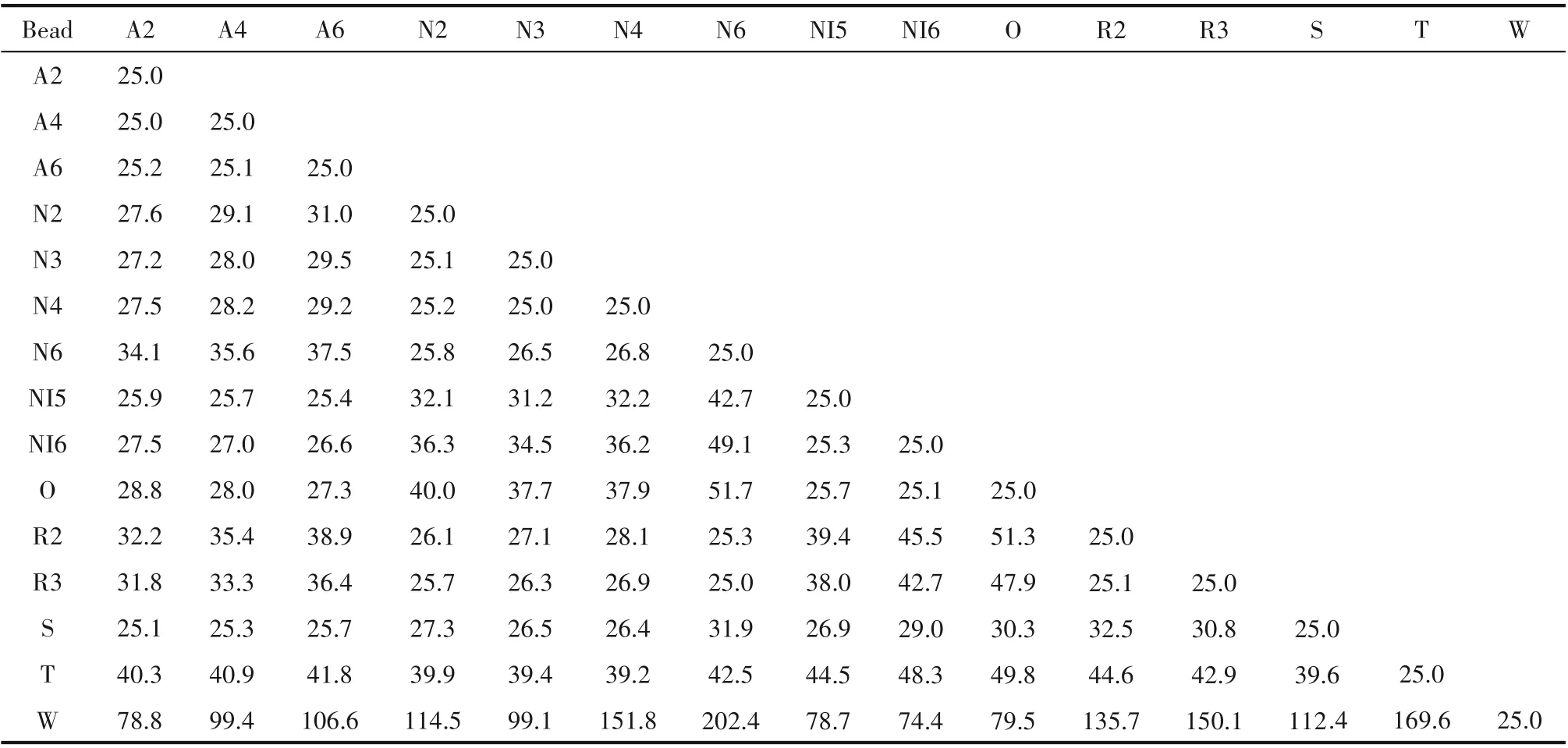
表1 DPD珠子间的保守力参数Table 1 Conservative force parameters between DPD beads

1.3 模拟体系

为了得到重质油的微观聚集结构与分子行为的关系，由于不能穷尽重质油的所有分子结构，过去的基础性研究工作普遍基于四组分（饱和分、芳香分、胶质和沥青质）模型展开。采用四组分平均分子结构模型表达重质油体系不仅可以降低体系计算量，还可以较好地与文献结果对比。因此，本文选用重质油四组分平均分子结构构建重质油体系，所采用的重质油四组分平均分子结构与前期工作一致，符合重质油分析数据与理论模型，如图2所示[34]。

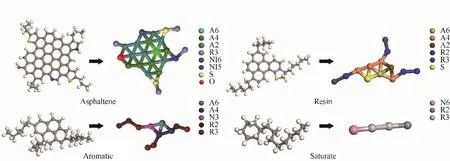
图2 重质油四组分粗粒化平均分子结构Fig.2 Coarse-grained model for SARA component

对于重质油的稳定性与其四组分含量的关系，Stankiewicz 等[2]根据现场经验与实验观察，总结了230 种重质油的稳定性规律，最终形成重质油稳定性判定图，如图3（a）所示。位于图中曲线下方的实验点为稳定重质油，曲线上方的实验点为不稳定重质油。然而，图中实验点仅能确定重质油四组分中两种组分的比值关系，四组分之间的比值关系不唯一。与此同时，胶体不稳定指数（C.I.I.）也同样存在四组分比值不唯一的问题，C.I.I.值计算公式如下[3]：

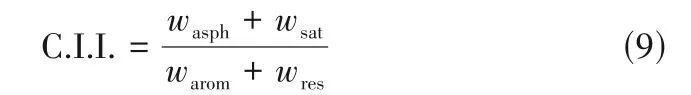
式中,w为质量分数，%。分子部分为沥青质与饱和分质量分数之和，为胶体不稳定组分；分母部分为芳香分和胶质质量分数之和，为胶体稳定组分。Asomaning 等[3]指出，C.I.I.值小于0.5 时，大部分情况下重质油十分稳定，C.I.I.值大于1.0 时，大部分情况下重质油不稳定，当C.I.I.值在0.5～1.0 时，重质油处于亚稳状态。

为避免重质油四组分比例不唯一的问题，本文结合两种方法，提出模拟体系，如图3（b）所示。该图是在重质油稳定性判定图的基础上加入了等C.I.I.值的一系列曲线，在曲线上取一系列试验点以覆盖重质油稳定性判定图。图中各系列直线（虚线）的通式为：

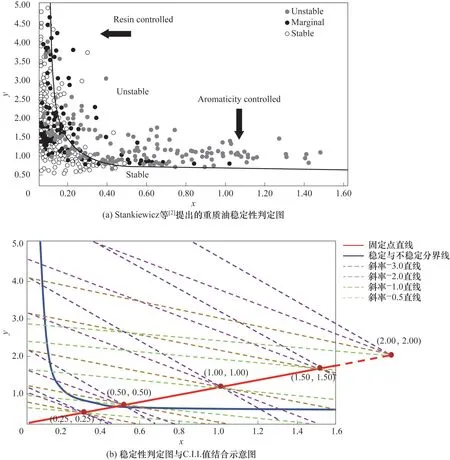
图3 重油稳定性判定图与模拟体系选取示意图Fig.3 Diagram of heavy oil stability determination and selection of simulation system

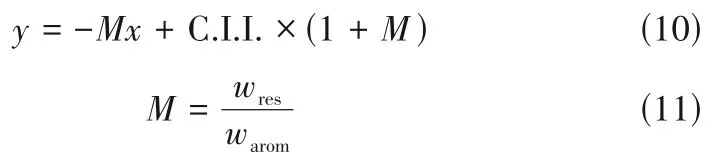
其中，x为wasph∕wres；y为wsat∕warom，与重质油稳定性判定图中的横纵坐标一致。

该图具有以下特点：

（1）当C.I.I.为定值时，所有斜率不同但C.I.I.值相同的曲线过定点（C.I.I.，C.I.I.），称过定点（C.I.I.，C.I.I.）与原点的直线为固定点直线；

（2）当C.I.I.值大于1.00 时，大多数试验点位于重质油稳定性判定图中的不稳定区；

（3）当C.I.I.值小于0.50 时，大多数试验点位于重质油稳定性判定图中的稳定区；

（4）当C.I.I.值在0.50～1.00 时，大多数试验点位于重质油稳定性判定图中的亚稳区。

以上特点说明，C.I.I.与重质油稳定性判定图在一定程度上判定效果相当。根据此图，确定本文所采用模拟体系如表2 所示，共99 组模拟体系。表中的第1～16 组模拟体系对应着固定点直线上的4 个数据点，C.I.I.值从0.25 到1.50，分别取M=0.5，1.0，2.0 和3.0，用于将模拟结果与C.I.I.值进行对比。其余模拟组，为C.I.I.值为0.25～2.00 时，图中虚线部分间隔一段距离选取的模拟点，用于将模拟结果与重质油稳定性判定图作比较。

表2 模拟体系Table 2 Simulation systems

2 结果与讨论

2.1 DPD计算结果与C.I.I.值的比较

图4 展示了第1～16 组模拟体系重质油微观聚集结构，为了便于观察沥青质的聚集情况，图中仅显示了沥青质分子。可以看出，随着C.I.I.值的增大沥青质的聚集程度增加，这与C.I.I.值的判定效果是一致的。然而，C.I.I.的定义式中没有考虑到胶质与芳香分的比值对沥青质聚集率的影响，从重质油的微观聚集结构中可以观察到，随着胶质与芳香分比值的增加，沥青质的聚集程度增加。

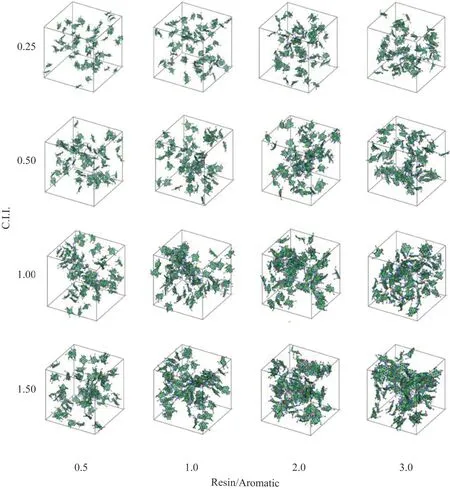
图4 第1～16组模拟体系重质油微观聚集结构Fig.4 Heavy oil aggregation structure of simulation systems 1—16

前期工作表明，在当前模拟体系下沥青质发生聚集时的分子间距离为4.4 Å[34]。因此，本文将分子间距小于4.4 Å作为统计沥青质聚集率的依据，统计结果如图5 所示。同种沥青质聚集率随C.I.I.值变化曲线表明，沥青质的聚集率与C.I.I.值成正比，当C.I.I.值大于0.50 时聚集率均大于5%，当C.I.I.值大于1.00时聚集率均大于15%，这与C.I.I.的预测效果也是相符的。可以认为，在当前模拟体系下，沥青质的聚集率大于15%时，重质油处于不稳定状态，沥青质聚集率小于5%时，重质油处于稳定状态，沥青质聚集率介于5%与15%之间时，重质油处于亚稳状态。胶质与芳香分的比值对沥青质聚集率影响存在极限，在胶质与芳香分比值小于2.0 时，沥青质的聚集率与胶质与芳香分比值成正比。当体系胶质与芳香分的比值大于2.0 时，随着胶质与芳香分比值的加大沥青质的聚集率并未明显增大。

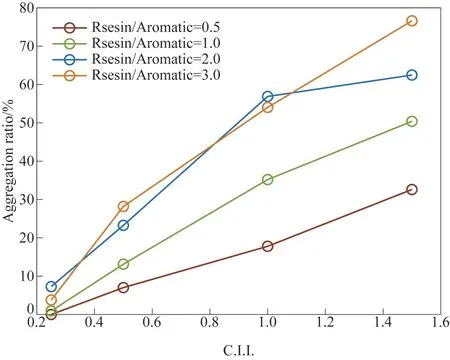
图5 沥青质聚集率随C.I.I.的变化Fig.5 Change of asphaltene aggregation rate with C.I.I

2.2 DPD计算结果与稳定性判定图的比较

为了将DPD 计算结果与稳定性判定图进行比较，本文统计了17～99组重质油微观聚集结构。图6展示了具有代表性的重质油微观聚集结构，可以看出，当沥青质含量达到一定值时，随着沥青质含量的增加，沥青质聚集率增大，当沥青质含量不高时，沥青质的聚集率与四组分的含量有关。统计四组分含量对沥青质聚集率的影响，如图7 所示。结果表明，当沥青质含量达到一定值时，沥青质的含量直接影响其聚集率，符合Yen-Mullins模型。当沥青质含量较低时，不可以忽略除沥青质外的其他组分对沥青质聚集率的影响。

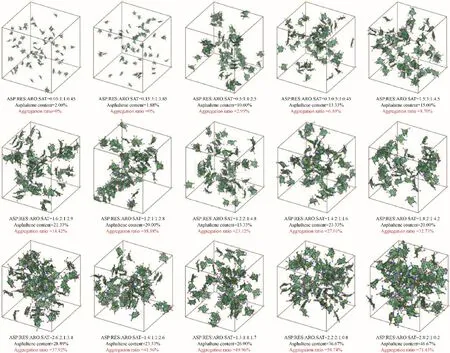
图6 第17～99组模拟体系代表性重质油微观聚集结构Fig.6 Typical heavy oil aggregation structure of simulation systems 17—99

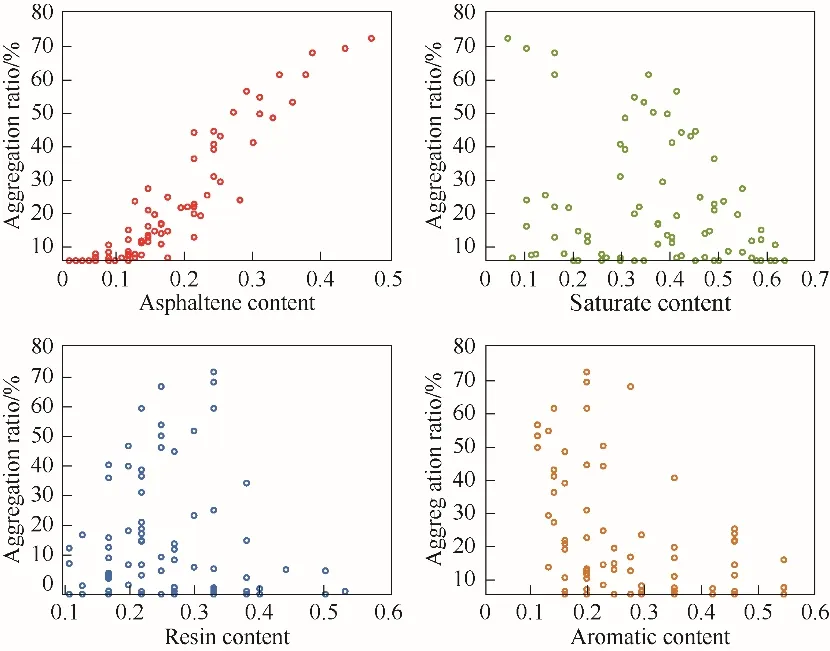
图7 四组分含量对沥青质聚集率的影响Fig.7 Effect of SARA content on asphaltene aggregation ratio

为了将模拟结果与重质油稳定性判定图进行比较，统计了17～99 组模拟体系的沥青质聚集率如图8 所示。在低Asphaltene∕Resin 值时，沥青质的聚集率均比较小，其中完全不聚集的模拟点多位于重质油稳定性判定图中分界线附近。但是当Asphaltene∕Resin 值增大时，模拟结果与重质油稳定性判定图存在不一致的情况。模拟结果表明，在高Asphaltene∕Resin 值且位于重质油稳定性判定图曲线下方的点出现了沥青质聚集率较高的情况。然而，原始的重质油稳定性判定图在这一部分没有试验数据，说明DPD 模拟结果证明了重质油稳定性判定图的局限性。从理论角度分析，当Asphaltene∕Resin值较大时，体系的沥青质浓度和沥青质聚集率也会较大，说明DPD 模拟结果是合理的。总地来说，DPD 模拟的结果与重质油稳定性判定图的试验数据基本吻合，同时弥补了重质油稳定性判定图的不足。

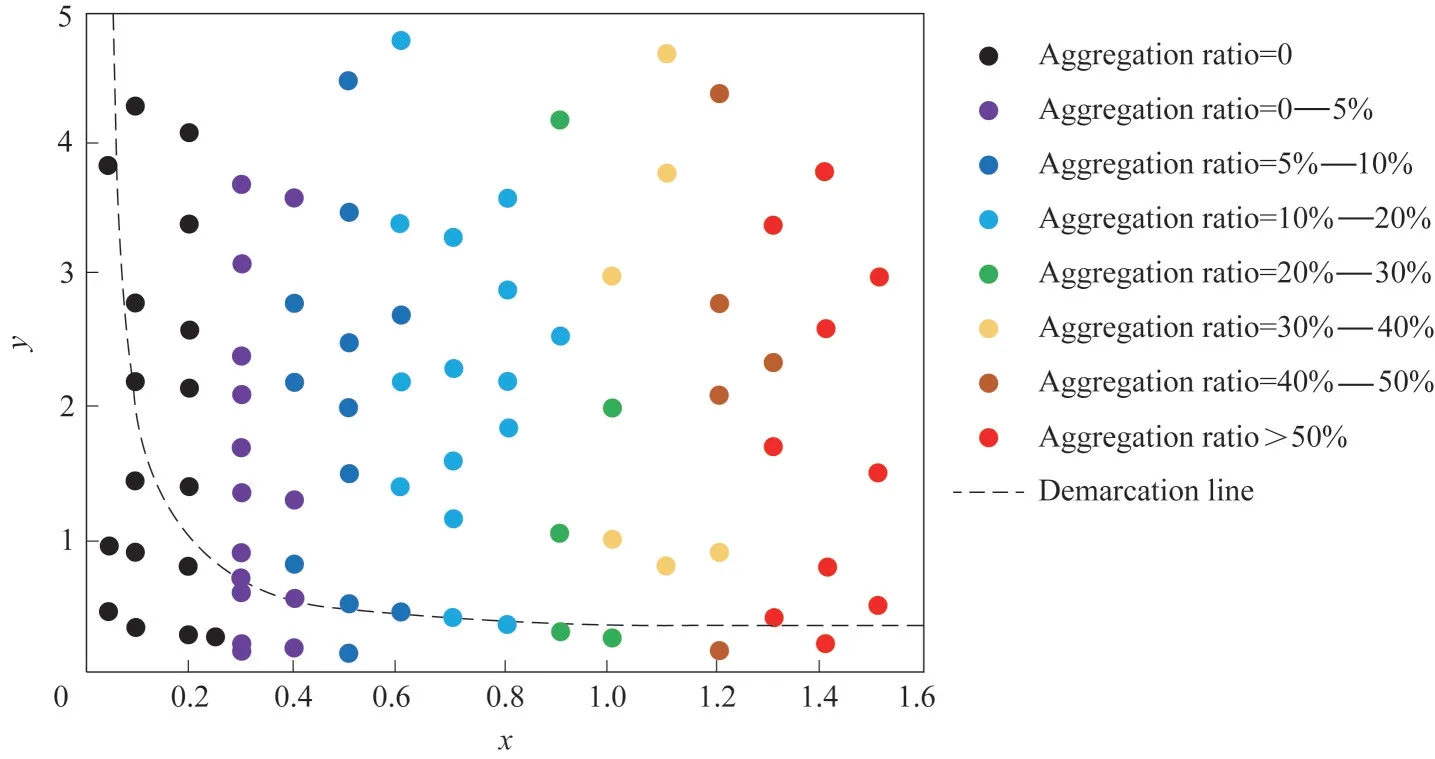
图8 第17～99组模拟体系沥青质聚集率统计结果Fig.8 Statistical results of asphaltene aggregation rate of simulation systems 17—99

2.3 重质油稳定性经验判据的改进

基于上述讨论，发现DPD 模拟结果可以用于判定重质油的稳定性，将沥青质的聚集率5%作为稳定与亚稳状态分界点，沥青质的聚集率15%作为亚稳与不稳定状态分界点是合理的。DPD 模拟结果可有效补充重质油稳定性判定图与C.I.I.的不足。因此，基于本文模拟结果提出改进的重质油稳定性经验判定图，如图9所示。图中两条曲线，蓝线为原重质油稳定性判定图的曲线，绿线为根据模拟结果统计，平行于蓝线画出的分界线，两条线将图中分成3个区域。对于重质油稳定性的判断可参照下述判定法：

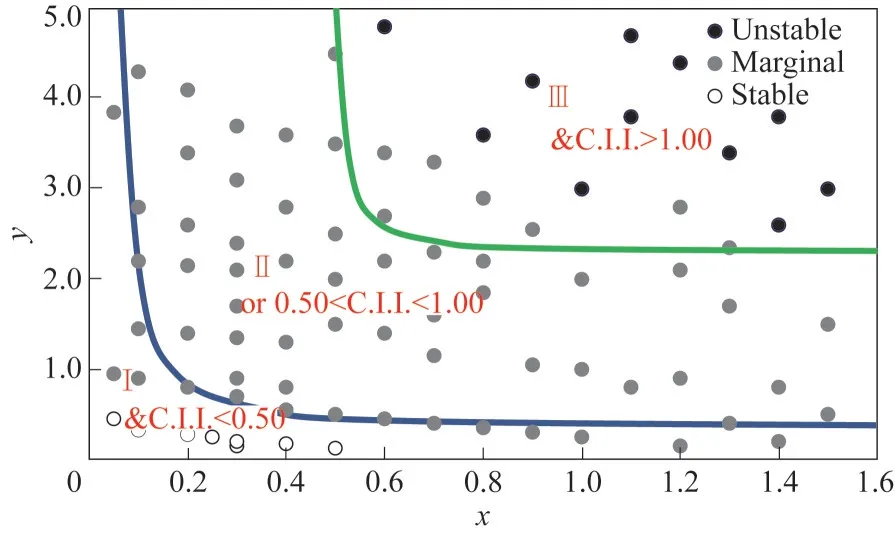
图9 改进的重质油稳定性判定图Fig.9 Improved stability judgment diagram of heavy oil

（1）当C.I.I.值小于0.50 且位于图中Ⅰ区时，重质油体系绝对稳定；

（2）当C.I.I.值大于1.00 且位于图中Ⅲ区时，重质油体系绝对不稳定；

（3）当C.I.I.值小于1.00且大于0.50或者位于图中Ⅱ区时，重质油的稳定性不确定，可以采用DPD模拟得到重质油的稳定性情况。

3 结论

本文基于耗散粒子动力学法模拟了不同四组分含量下重质油体系的微观聚集结构，并由微观聚集结构统计沥青质分子聚集率，用于重质油稳定性的判定。结果表明，基于DPD 模拟得到的沥青质聚集率与C.I.I.值成正比，证明了本文选用的模拟体系的准确性。将沥青质聚集率与C.I.I.值对比得到重质油稳定性判定标准，当体系沥青质聚集率大于15%时，重质油不稳定，沥青质聚集率小于5%时，重质油稳定，沥青质聚集率介于5%与15%之间时，重质油处于亚稳状态。选取83 组模拟结果与重质油稳定性判定图对比，结果表明，本文模拟体系得到的沥青质聚集率与重质油稳定性判定图结果较为吻合，DPD 模拟可有效补充稳定性判定图的不足。基于DPD 模拟结果，本文提出了改进的重质油稳定性判据，用于重质油稳定性的快速判定，本文提出的重质油稳定性判定方法有望实现工业应用。

符号说明