优化教学思考设计促进学生思维发展
2022-11-11陶柱中
陶柱中
[摘 要]在小学数学课堂教学中,要想充分激活学生思维,引发学生思考,就必须精心对教学过程进行设计,做到课前情境创设有广度,课中引领有梯度,课后反思有深度。只有让思考充盈课堂,才能引领学生乐于思考、善于思考,学生的数学素养才能真正落地生根。
[关键词]教学思考;教学设计;思维
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2022)23-0081-03
引领学生思考,促进学生思维品质的提升是教学的目标,同时也是实现高效教学的关键要素。笔者从事小学数学教学三十余年,一直潜心设计数学思考,力争使数学课堂成为引领学生思维发展的浩瀚海洋。下面就笔者的实践和思考,略表浅见。
一、教学过程用“思考”设计
获得成功在于运筹,获取经验在于反思,驾驭课堂在于机巧变通。要想让学生的思考充盈教学全过程,焕发课堂生机,教师可从课前、课中、课后三方面进行精心设计。
1.课前创设思考要有广度
数学课程标准明确要求学生运用数学的思维方式进行思考,增强发现问题、提出问题、分析问题和解决问题的能力。为了在课前导入环节就能充分带动学生思考,教师需要创设数学问题情境,将数学问题与现实生活联系起来,让学生尝试用数学方法解决具体问题,从而进一步体验数学的价值所在。
例如,在教学北师大版数学三年级上册“里程表”时,笔者先在课前查阅了大量的相关资料,再将涉及本课内容的各种问题进行了初步的拟定,并对问题进行了创设:
(1)生活中还有哪些问题与里程表问题相似?
(2)电表、水表、燃气表每月使用的量能否用里程表问题的解决方法来解决?
(3)计算里程表问题要重点把握哪三个量?这是否和以前所学的时间计算运用了同样的方法?
(4)计算里程表问题时,能否运用线段图将计算方法简洁地表示出来?从中你发现了什么?
在设计以上问题时,笔者集合本班学生的学情进行了初步判断:有的学生会仅囿于课本,或局限于对生活的感知,不能将数学问题进行有效发散,如有的学生会认为里程表问题仅仅就是计算汽车、火车等交通工具行驶的里程。可见,教师只有通过提出一系列的问题,提升课前创设问题的广度,才能在课堂上引领学生进行思考与探究,将新知和旧知紧密关联起来,培养学生思维的广阔性。如将里程的计算和以前的时间计算有效关联,并运用线段图建立起数学计算模型,把握住零起点和非零起点的两种数学问题的本质,逐步引导学生对数学本质的理解,最终激发学生对数学学习的浓厚兴趣。
2.课中引领思考要有梯度
在课堂教学过程中,要想充分发挥学生的主体作用,让学生在课堂之中积极地进行思考与探究,教师就要巧设问题思考的梯度,实现新旧知识的衔接和合理迁移,这对学生接受新知至关重要。引领学生对梯度性的问题进行思考,能够让学生的思维变得更加具有层次性、灵活性和逻辑性。
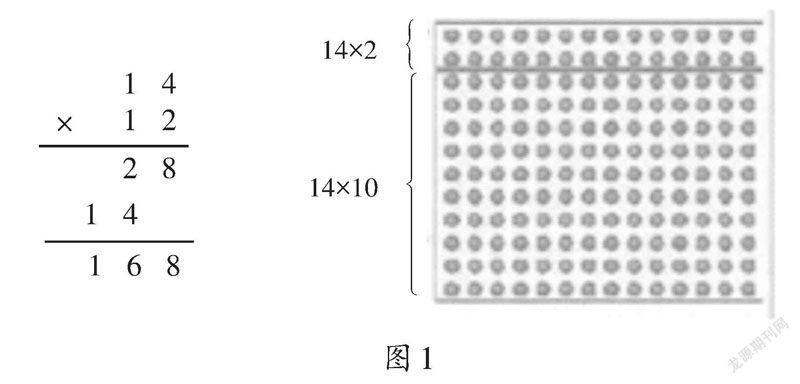
例如,在教学北师大版数学三年级下册“两位数乘两位数”时,笔者便对旧知识的迁移进行了梯度式的设计,引发学生进行梯度式的思考,进而培养学生的推理能力。笔者在出示“14×12”后,先要求学生在点子图中圈一圈(如图1),然后提出問题:“14×2是多少?12中的‘1’表示的数值是多少?14×10=140在竖式中可以怎样写?为何要把两次乘得的积加起来(可联系点子图的圈法进一步启发思考)?”引发学生进行梯度性的思考。在问题的引领下,学生进行反复思考与探究,最终全面掌握乘法的算理。
又如,教学“约分”时,笔者利用问题一步步引领学生深入思考。
师:对一个分数进行约分时,依据我们前面学过的什么知识进行约分?
生1:依据的是分数的基本性质。
师:那么分数的基本性质又是根据什么知识推导而来的呢?
生2:根据商不变的规律推导而来的。
师:商不变的规律和分数的基本性质又是如何产生关联的呢?
生3:根据分数与除法的关系。
教师通过一系列的追问推进学生思维的发展,让学生的思维得到有序进阶,使学生所学习到的知识变得更加系统化。引领学生进行梯度性的思考,能有效锻炼学生数学思维的敏捷性和批判性,提升数学学习能力。
3.课后反思设计要有深度
在每一节课教学结束后,教师需对本节课的教学进行总结和反思,如反思学生的思维能力是否得到充分的调动和训练,数学思考是否真正实现,学生的数学能力是否真正得以发展。这样的反思将利于后续课堂教学的改进。当然,引发学生思考,让整节数学课充盈思考味绝非易事,因此在课后反思时,教师更要进行深度总结,总结包括自己在课前预设的思考问题是否全面,课中思考的引领是否到位,等等。
例如,在整理北师大版数学三年级上册“加与减”的教学设计时,笔者对各环节进行反复思考。例如:在“捐书活动”问题中,三个数连加的计算要注意哪些细节;在“运白菜”问题中,三个数连减的运算要注意哪些细节;在“结余多少钱”问题中,加减混合运算又要注意哪些细节;学生在课堂中对这些问题都进行了深入的思考了吗,又提出了哪些问题,问题解决了吗,哪些存入了“问题银行”;学生在计算中为什么出现了这样的错误,他们到底是怎样思考的。教师对课堂中学生的思考情况进行一一归纳和反思,有利于在单元整理和复习中进行查漏补缺,同时也能对学生的思考和疑问进行及时理答,进一步鼓励学生积极思考,将学习到的数学知识应用到解决实际问题中。通过这样的反思,教师能够不断积累课堂教学经验,进而提高课堂教学效率。
二、教学重点用“思考”深入
在课堂教学中,知识技能的掌握既是学生发展的基础性目标,又是落实数学思考目标的载体。因此,教师需要针对教学中的重点内容引导学生进行猜想、推理、验证、归纳等。在此过程中,激发学生深入思考和探究就显得格外重要。
例如,在教学北师大版数学四年级下册“三角形内角和”时,笔者将教学重点放在引导学生对三角形内角和的探究过程中。笔者先出示一组大小不等的三角形进行动画演示,并提出问题:“3个三角形都说自己的内角和最大,谁说的是对的呢?”这无疑激发了学生进一步探究的欲望。接着,笔者启迪学生用实际测量的方法来探寻,当学生得出不同的数值(均在180°左右)时,向学生提问:“得出不同数值的原因是什么呢?”这一问题使教学重点内容得以推进,学生发现原来是他们在测量过程中出现了误差。最后,笔者引导学生通过剪拼的方法来实际验证,学生发现:任意三角形的三个角拼在一起构成的都是一个平角。在整个教学过程中,笔者通过猜想、质疑、探究和验证的活动,将教学重点不断引入深处,学生的思维也实现了从直观形象向抽象合理过渡,思维品质得以提升。只有整个教学过程充盈着思考味,用思考来突出教学重点,学生思维的积极性才会被充分调动。
又如,在教学北师大版数学六年级上册“百分数”时,笔者首先明确了该章节教学的重点是让学生认识到百分数的概念、内涵以及表示方法,并且掌握最为常见、基础的百分数在生活中的广泛应用。于是笔者先让学生了解百分数与分数之间的区别与联系,在学生了解了百分数的概念及内涵后,再让学生联想百分数在实际生活中的应用,并思考百分数在折扣问题中是怎样使用的,最后引领学生进行深入思考:当班级中学生的成绩出来之后,老师是怎样运用百分数计算及格率的。大量的生活实例让学生感受到百分数在生活中的广泛运用;真实的具体情境让学生体验百分数出现的必要性和优越性,了解数学与生活的密切联系。这样的教学设计让学生对该章节所需要学习的知识进行深入思考与探索,进而帮助学生理解课堂教学中的重点内容,提高学生的数学学习能力。
三、教学难点用“思考”突破
在课堂教学过程中,教师需要采取恰当的方法引导学生进行思考,帮助学生解决各种问题,降低学习的难度,营造轻松愉快的学习氛围,这就需要充分激发学生的创造性思维,用“思考”突破教学难点。
例如,在教学北师大版数学四年级下册“三角形三边的关系”时,笔者明确了本课的教学难点是如何在实验活动中让学生去探索并发现“任意三角形两边之和大于第三边”。为了突破这一教学难点,笔者设计了摆小棒的活动,这引发了学生思考:为什么有的三根小棒可以围成三角形,而有的三根小棒不能围成三角形呢?为了突破这一认知冲突,筆者让学生一边摆小棒一边记录数据,通过数据分析形成个人见解,继而在小组中讨论交流,最后形成结论,这样就有效地突破了教学难点。
又如,在教学北师大版五年级上册“组合图形的面积”时,虽然学生已经掌握了一些基本的组合图形的面积计算方法,但是对于一些复杂的组合图形的面积,学生就会感到有难度。于是笔者借助多媒体设备展示各种组合图形,让学生对构成这些组合图形的基本图形先进行分析探讨,再思考每一个组合图形是由哪些基本图形构成的,最后学生就可以在思考与探索的过程之中逐步掌握组合图形分解的方法及技巧。如此,便有效地降低了组合图形面积计算的难度。这样的教学方式能够引领学生进行针对性的思考,从而突破教学中的难点。
四、引领学生乐思、善思,让数学素养落地生根
在小学阶段的课堂教学中,教师需要将学生数学核心素养的培养落实。采取有效的方式引导学生思考,能让学生在学习过程中乐于思考,当学生获得成功的体验后,就会主动思考数学问题,从而提高数学学习能力。
例如,在教学北师大版数学五年级上册“轴对称和平移”时,笔者引导学生先观察课本中的平面图形,然后复习轴对称图形的概念,最后对课本中所展示的平面图形进行观察与判断,思考这些图形是否属于轴对称图形。大部分学生对图形非常感兴趣,此时笔者引导学生先将纸张进行折叠,用剪刀任意剪出一个图形,再将纸张摊开,观察其是否是轴对称图形。有的学生在观察的过程中发现,将有些轴对称图形进行旋转就可以将斜线或者竖线作为新的对称轴。通过这样的方式开展教学,能够引领学生从不同的角度思考数学问题,同时也能够在理论与实践结合的过程中,让学生体验到思考的乐趣。
又如,在教学北师大版数学四年级下册“小数乘法”时,其中涉及“2.4×0.85=?”和“1.2×1.25=?”两道计算题。用竖式计算出这两道题的结果,对学生来说难度不大,于是笔者让学生将运算结果与乘数2.4、1.2作大小比较。
师:为什么2.4×0.85的积比2.4小,而1.2×1.25的积比1.2大?
生1:因为0.85<1,所以2.4×0.85<2.4;因为1.25>1,所以1.2×1.25>1.2。
生2:2.4×0.85就是求2.4的0.85倍是多少,0.85倍还不到1倍,所以2.4×0.85<2.4;1.2×1.25就是求1.2的1.25倍是多少,1.25倍已经超出了1倍,所以1.2×1.25>1.2。
生3:2.4×0.85就是求2.4的85/100是多少,也就是把2.4平均分成100份,求其中的85份是多少,还没有占到全部的份数,所以2.4×0.85<2.4;1.2×1.25可以写成1.2×(1+0.25),运用乘法分配律展开后是1.2×1+1.2×0.25,可见1.2×1.25>1.2。
正是由于学生的乐于思考、善于思考,他们的思维才得以发散,并言之有理,使得运算思维具有深刻性。虽然学生在数学语言的表达上不够精准,但其数学思维的灵活性得到了锻炼——灵活运用数学方法解释数学计算过程和结果,尤其是生3的解答更具有数学的推理性。笔者对以上学生的解答思路均进行了深刻的剖析,肯定了他们的数学推理成果,并适时表扬了他们勇于积极钻研的数学探究精神。可见,积极引领学生乐于思考,可让学生积累数学经验,从而善于思考,进一步提升数学学习能力,让学生的数学素养真正落地生根。
总之,数学思考是一堂数学课的灵魂,展现出的是教师对数学及数学教学的深刻认识。在数学课堂教学中,教师扮演的引导角色是非常重要的,可以让学生对各种数学问题进行思考,让思考充盈数学课堂,激发学生的无限学习热情,让学生的数学思维得到锤炼,数学素养得到提升,让数学教学目标真正得以实现。
