把握教学要点,有效培养学习力
2022-11-11吴红艳
吴红艳

[摘 要]学生的学习力可以分为显性学力和隐性学力,当下的课堂普遍存在重显性轻隐性的现象,对学生隐性学力的培养远远不够。隐性学力的培养不能忽视,教师应更加关注学生思维方式、探究能力、创新精神、数学意识和数学理性等隐性学力的有效生长,促进学生数学素养的全面提升。
[关键词]小学数学;隐性学力;数学素养
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2022)23-0090-03
陶行知先生说:“教育就是力的表现。”这里的“力”指的是学习力。所谓学习力是指在学问上达到的程度,是学生借助学校内外的学习过程所习得的能力的总体。日本学者木下繁弥把学力分为显性学力和隐性学力,其中显性学力是指可量化考查的知識技能方面的学习结果,隐性学力是指在掌握知识技能的过程中所获得的学习潜力,即思维方式、探究能力、创新精神、数学意识和数学理性等,表现为对将来学习的作用。用朱永新教授的话来说,显性学力是看你跑得“快不快”,而隐性学力则是关注你跑得“远不远”。
当下部分课堂还存在“知识至上、技能至上、分数至上”的教学倾向,对学生隐性学力的培养远远不够。笔者认为,隐性学力的培养不容忽视,教师要更加关注学生学习品格、思想方法、意识和价值观的有效生长,促进学生数学素养的全面提升。
一、点燃探究欲望,在发现中夯实素养之基
数学课程标准指出:“学生学习应当是一个生动活泼的、主动的和富有个性的过程。认真听讲、积极思考、动手实践、自主探索、合作交流等,都是学习数学的重要方式。”教师要站在学生立场去理解学生、成全学生,在有趣的发现之旅中激发学生的探究欲望。
【案例1】“有趣的乘法计算”教学片段
师:同学们,这节课老师想先和大家交换一下角色,我当学生,你们当老师来考考我好不好?
(学生的热情一下子被点燃)
师:你们任意出一个两位数乘11的算式,看老师能不能直接说出答案。
生1:52×11。
师(学生刚说完算式,笔者就快速报出了答案):572。
生2:38×11。
师:418。
生3:老师,你太厉害了!
生4:老师你是怎么做到的呀?
师:其实,要做到老师这样一点儿也不难,相信通过接下来的探究,你们也能像老师一样答得又快又准。
(至此,学生的探究欲望被充分激发,他们迫不及待地投入接下来的发现之旅中)
师:请大家先笔算出24×11、53×11、62×11的积,再把积每一位上的数和两个乘数相比较,你有什么发现?在小组内交流你的发现。
(学生探索后交流汇报自己的发现)
生5:我发现积个位上的数与第一个乘数个位上的数相同,积百位上的数与第一个乘数十位上的数相同。
生6:我发现积十位上的数是第一个乘数个位和十位上的数之和。
师:我们可以把这个发现形象地概括为“两头一拉,中间相加”。
在此环节中,笔者通过课前的角色置换激发了学生学习数学的内在动力,充分点燃了学生的探究热情,并引领学生由“趣”生“需”,使其经历了主动的探索过程,对两位数乘11的计算规律有了清晰的认知。
二、诱发创新精神,在生成中构建素养之型
创新精神十分重要,落实到课堂上,笔者觉得应该培养学生主动获取知识的意识和灵活运用知识解决问题的能力,使学生不断发展创新意识。教师可以通过介绍一些不断自我创新的人物鼓励学生,诱发学生的创新精神。
例如,笔者在课堂上介绍齐白石,他本是个木匠,靠着自学成为画家。然而,面对已经取得的成功,他从不骄傲自满,而是不断汲取历代名家的长处,改变自己的作品风格。齐白石60岁以后的画,明显不同于60岁以前的;70岁以后,他的画风又变了一次;80岁以后,他的画风再度变化。据说,齐白石的一生,曾五易画风。正因为齐白石老人在成功后仍然不停创新,所以他晚年的作品比早期的作品更为成熟,形成了独特的流派与风格。
【案例2】“长方形的周长”教学片段
师:从一张长10厘米、宽7厘米的长方形纸上剪下一个最大的正方形,剩下图形的周长是多少厘米?
生1:我在练习纸上画图后发现,剪下的最大的正方形边长和长方形纸的宽相等,是7厘米,剩下的图形是一个小长方形,小长方形长7厘米、宽3厘米,剩下图形的周长是(7+3)×2=20(厘米)。
师:还有不同的方法吗?
师:如果我把“宽7厘米”这个条件改成“宽6厘米”,现在剩下图形的周长是多少厘米?
生2:剩下的图形是一个小长方形,长6厘米、宽10-6=4(厘米),剩下图形的周长是(6+4)×2=20(厘米)。
生3:宽改变了,剪下的最大的正方形边长也变了,剩下的小长方形的周长怎么还是20厘米呢?
师:如果我将“宽7厘米”这个条件去掉,还能求出来吗?
生4:我知道原因了。剩下的小长方形的长和剪下的正方形的边长相等,所以小长方形一条长和一条宽的长度合起来就是原来长方形的长,不管原来长方形宽是几厘米,小长方形的周长只要用原来长方形的长乘2就可以了,列式为10×2=20(厘米)。
创新的解题方法给学生带来了强烈的震撼,学生感受到了创新的魅力,体验到了创新的乐趣。课堂上换个角度思考问题,打破常规来解决问题,常常会有意想不到的收获。教师要给予学生充分的信任和尊重,让学生激活、生成应有的创新精神。
三、培养思维能力,在发展中塑造素养之品
在课程改革的背景下,教师需要把数学知识的教学转移到数学思维活动的过程中来。数学教学既要培养、发展学生的逻辑思维能力,又要培养学生的直觉思维能力,要把数学思维过程充分地暴露在学生面前,优化教学过程,提高教学效率,推进小学数学学科素质化的进程。
【案例3】练习题“一本故事书有192页,小明每天读24页,读了5天后还剩多少页?”教学片段
(一个学生自告奋勇上台板演,他刚列式192÷24,其他学生就哄堂大笑)
师(止住哄笑,引导学生顺着其思路往下想):大家安静一下,想一想,192÷24的结果是什么?
生1:结果是8,表示小明如果每天读24页,那么读完这本书一共要8天。
师:小明已经读了5天,还要几天读完呢?
生2:8-5=3(天)。
师:还剩多少页没读?
生3:24×3=72(页)。
(于是,列式变为24×(192÷24-5),一种极具创造性的解法诞生了,这个学生也在大家的掌聲中回到了座位上)
在这个环节中,笔者善于捕捉学生的思维轨迹,不仅挽回了学生的面子,而且拯救了稍纵即逝的直觉思维火花。长期以来,部分教师总认为小学生的思维必须严密、完整,培养逻辑思维能力才是数学教学的目标,因而许多直觉思维的火花被忽视或被无情地浇灭。布鲁纳说:“应当尽可能地从最早年级起发展学生的直觉规则。”因此,教师要在思想上纠正认识偏差,对学生思维活动的规律多加研究,并有意识地培养学生的直觉思维。
四、催化数学意识,在形成中润泽素养之魂
在数学教学中,教师要将抽象的概念、法则、定律等要素置于学生熟悉的生活情境中,引导学生观察分析、归纳概括,以解决生活问题的策略为依据,探寻潜在的数学原理,发觉内隐的数学本质,形成自觉的数学意识。
【案例4】“四则混合运算”教学片段
(为了让学生更好地理解“先乘除后加减”,笔者设计了如下环节)
师:我们已经会算300-65×4这道算式了,你能用这道算式创编一道情境题吗?
(学生思考、编题,笔者组织学生交流)
生1:甲地到乙地有300千米,汽车从甲地出发,每小时行驶65千米,行驶了4小时,距乙地多少千米?
生2:李老师带了300元到体育用品商店买篮球,每个篮球65元,买了4个,付300元的话营业员应找回多少元?
生3:学校购置了300本图书,分给三年级4个班每班65本后,还余多少本?
师(等学生交流完毕,引导学生思考):如果解这些情境题时先算减法,会出现什么情况呢?
(学生明白“先乘除后加减”不只是对混合运算的运算顺序的一种简单规定)
学生创编情境题的过程是数学原理与现实生活合理相遇的过程,也是将算理与生活相结合的过程,更是理解、深化算理的过程。此时,数学意识就如种子般在学生的心间萌芽、生长。
五、内化数学理性,在审慎中丰厚素养之本
数学理性有着重要的价值,数学教学应以理性的力量去感召学生,引领学生在数学知识的发生与发展过程中沉下心来思考:是什么、为什么、怎么做。
【案例5】“长方形和正方形的面积”教学片段
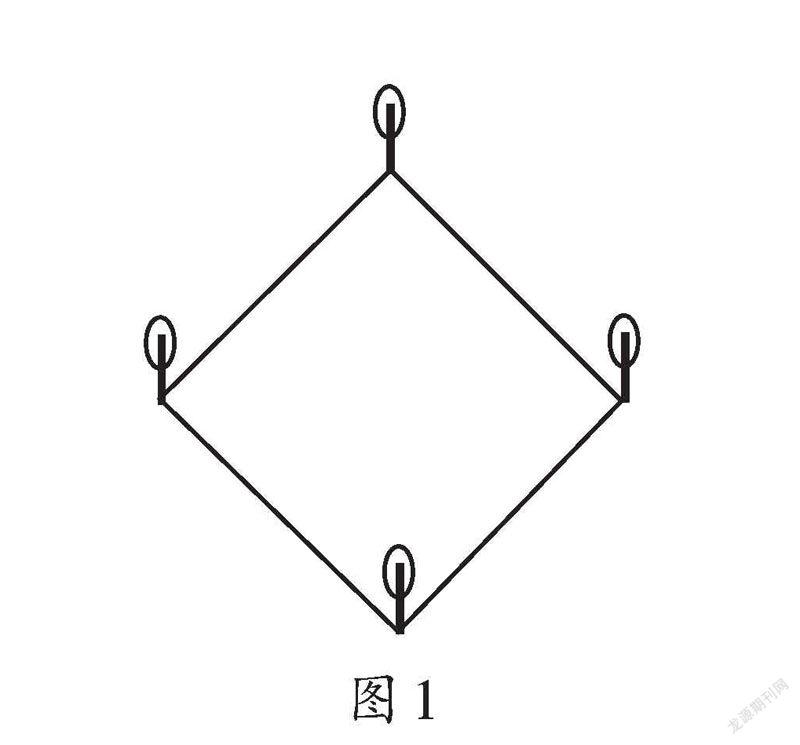
师(出示图1):青湾村有一个正方形养鱼池,在养鱼池的四角都栽有一棵树。现在要在不移动这4棵树的情况下扩大养鱼池,扩大后的养鱼池的形状仍然是正方形,面积是原来的2倍。能做到吗?
(学生思考并尝试画图)
生1(上台演示自己的做法,示意图如图2):我觉得可以这样做。
生2:这样4棵树不都在水里了吗?
生1:可以在树根处留一点泥土,这样树就不在水里了,还可以继续生长。
(此时,学生关注点只是树是不是长在水里,显然,他们对这个问题的认识还停留在感性的表面上,未从理性的角度去深入思考问题的本质)
师:这道题目除了要考虑树的问题,还要抓住什么条件?
生3:扩大后养鱼池的形状仍是正方形,面积是原来的2倍。
师:那我们来看图2,符合这两个条件吗?
生4:扩大后的形状仍是一个正方形,但面积好像不是原来的2倍。
师:扩大后正方形的边长是原来的多少倍?面积是原来的多少倍?
生5:扩大后正方形的边长是原来的2倍,面积就是原来的4倍。
生6:可以将边长缩短一点,这样面积就是原来的2倍了。
师:那大家试试,看边长缩短到什么程度,面积就是原来的2倍。
(学生反复举例验证,可就是得不到结果。显然,三年级学生的学习水平还无法解决这个问题,但是笔者没有从一开始就否定学生的想法,而是让学生在反复的探索中明白为什么不可以这样做,更理性地去探求问题本质)
师:如果要把一个已知的正方形分成面积相等的两部分,其中一部分仍然是正方形,可以怎么做呢?
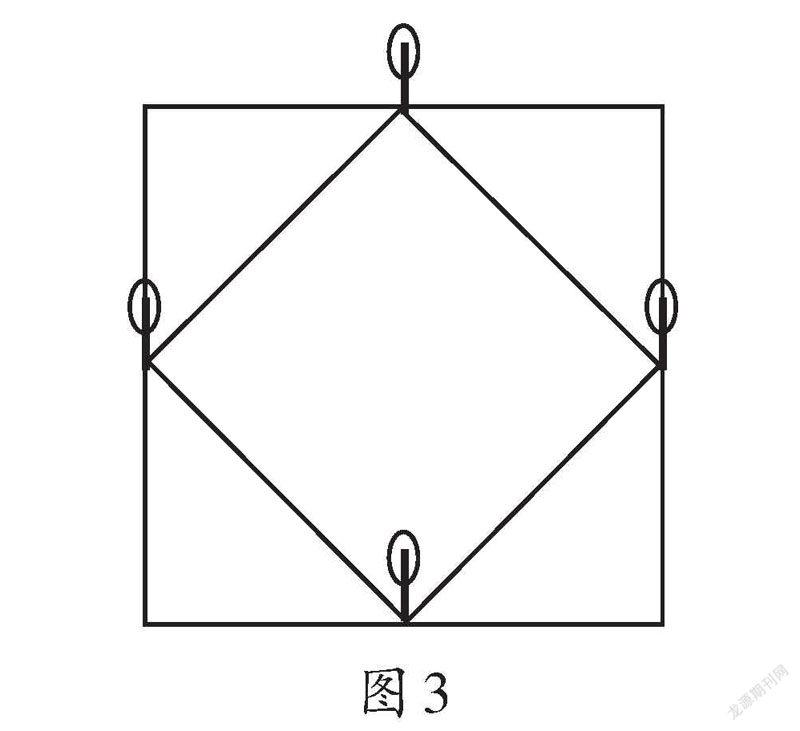
生7(画出了如图3的示意图):可以这样做。扩大后的养鱼池仍然是一个正方形,而且面积是原来的2倍;原来正方形4个顶点处的树位于扩大后正方形的边线上。
杜威曾指出:“在教学中,以外在的成果为标准的做法,表现在人们只重视‘答案正确’,从而使教师无法集中注意力去培养学生的理性思维。”因此,在数学课堂上特别需要教师重视数学理性的培养,使学生充分感受到数学理性的力量,从而将其内化为自觉的数学素养。
教育的根本目的在于促进人的全面发展,在于启迪人的智慧,给予人发展的方向、动力和潜力。培养学生的隐性学力,将使学生的数学素养逐步萌发、生长,使其核心素养内涵更趋完善,也为他们更好地应对未来社会和创造未来世界注入了新的动力、能力和智慧。
