构建“理趣课堂”的实践
2022-11-11邓芸芸
邓芸芸


[摘 要]“理趣课堂”是理性与感性有机结合的课堂。文章以斐波那契数列的教学实践为例,阐述了如何营造趣味课堂,引导学生去经历、去探索知识形成的过程,最终达到理趣相生的和谐状态。
[关键词]理趣课堂;斐波那契数列;小学数学
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2022)23-0060-03
“理趣课堂”,顾名思义就是富有理性和感性的课堂。理性主要是指数学课堂要有数学的理性精神,学生应带着求真的精神去探索研究数学,追求一种完全确定、完全可靠的知识;感性主要是指数学源于生活,数学课堂应该结合客观实际,体现其社会性、现实性、实践性、直观性,通过这些感性的和有趣味的客观认识激发学生学习数学的兴趣。“理趣课堂”,糅合了理性和感性,将课堂变得生机勃勃,增强了课堂的趣味性,大大提高了学生参与课堂的积极性和热情,有利于提高课堂教学效率和质量。
“理趣课堂”,努力做到用数学的理性精神引领学生去探索、去求真,去经历知识形成的过程;同时又遵循学生的认知规律,激发学生的探究热情,最终达到理趣相生的和谐状态。
现以“斐波那契数列”教学为例,谈谈如何构建“理趣课堂”。
一、激趣探理,发现数列
布鲁纳说:“兴趣是最好的老师。”小学生具有强烈的好奇心。课堂伊始创设有趣的问题情境,可激發学生的好奇心,让他们更快地进入新知的探索中。
1.设疑导入
师(出示比萨斜塔图片,如图1):意大利比萨不仅有闻名于世的斜塔,还出过一个伟大的数学家斐波那契。800多年前,他在著作《算盘书》中提出了一个有趣的兔子问题,吸引着人们不断地去研究。究竟这个兔子问题如何有趣呢?大家想知道吗?
2.出示问题
师(出示兔子问题):假设一对刚出生的小兔一个月后就能长成大兔,再过一个月它们便能生下一对小兔,而且以后每个月都会再生一对小兔。如果一年内没有发生死亡,那么12个月后会有多少对兔子呢?
3.初步尝试
师:遇到这样的难题怎么办?请大家联系以前的学习经验想一想。
生1:可以化难为易,将难题转化成容易解决的问题。
生2:可以先研究前几个月的情况,看看有没有什么发现。
4.发现规律
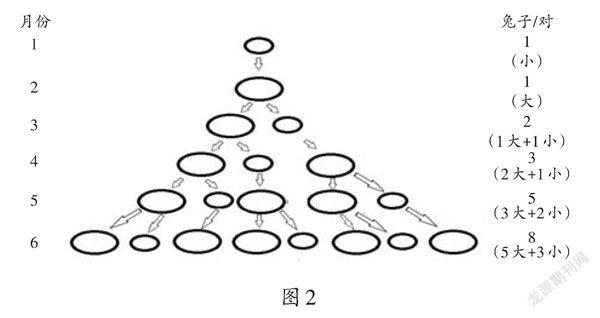
师:第1个月是什么情况?第2个月呢?第3个月呢?……第6个月呢?怎么知道的?(出示示意图,如图2)
生3:每个月大兔子的对数就是前一个月兔子的总数,小兔子的对数就是前一个月大兔子的对数,而前一个月的大兔子,又和再前面一个月兔子的总数一样。
生4:也就是说,每个月兔子的总数等于前两个月兔子的总数相加。
师:现在可以找到12个月后兔子的总数了吗?
生5:把前两个月兔子的总数相加就能得到下一个月兔子的总数。
师:怎么觉得后面的找起来反而容易了。
生6:因为我们在比较简单的部分发现了规律,所以在难的部分直接运用规律就可以解决问题了。可见难和易是可以互相转化的。
5.大胆猜测
师:猜一猜,如果所有的兔子都没有生病或老死,4年后会有多少对兔子?
(学生先猜测是几百、几千、几万,最后看到结果是48亿多时,都表示完全超出了预期,为这个结果感到震惊。)
师:大学者胡适说过,我们要大胆假设,小心求证。看来我们以后猜测的时候不妨再大胆一点。
6.揭示数列
师:这只是数学中的理想模型,实际生活中兔子当然会生老病死,但是这样的假设却给我们带来了有趣的数列。因为这个问题是数学家斐波那契提出的,所以这个具有规律的数列又叫“斐波那契数列”。
评析:在上述环节中,数学史上有趣的兔子问题牢牢地吸引着学生的注意力,引领学生主动提出化难为易的转化策略,运用画图、列举、计算等多种方法,通过独立思考与集体交流,探求了数量关系中蕴含的规律,并运用规律解决问题,成功找到著名的斐波那契数列。学生不仅知道了数列的数据特点,即从第三项起每一项都等于前两项的和,而且还结合情境做出了自己的解释。在此过程中,学生感受到了数学有理有据、逻辑严密的特点。尤为可贵的是,学生在探索的过程中感悟到难和易是相对的,是可以互相转化的,闪现出哲学思辨的火花,他们的理性精神在潜移默化中自然生长。
二、理中生趣,研究数列
1.分组研究数列的性质
师:斐波那契数列还有很多有趣的性质,从古至今,吸引着无数人进行研究。请4人为一个小组,每组选其中一个性质进行研究。
2.集体交流数列的性质
师:同学们发现斐波那契数列还有哪些有趣的性质?
生1:从第3项起,任意一项的平方与它前后两项的积总是相差1,有时是多1,有时是少1。
生2:第3、6、9项的数字,能被2整除;第4、8、12项的数字,能被3整除;第5、10项的数字,能被5整除;第6、12项的数字,能被8整除。
生3:能被2整除的项数都是3的倍数。
生4:相邻两个斐波那契数的平方和仍是斐波那契数,比如,22+32 就等于13,32+52就等于34。
生5:前一项除以后一项的商一直在变,如1,0.5,0.667,0.6,0.625,0.615,0.619,0.618……一会儿变大一会儿变小。
生6:感觉这个比值在越来越靠近一个结果。
生7:我认为它在靠近0.618 ,因为我又向后算了两次,得数分别是0.619、0.618。
生8:我听说过0.618这个数,它是黄金比。也就是说斐波那契数列的前后两项的比值越来越接近黄金比。
……
师:时间的关系,我们今天只研究了斐波那契数列的几个性质。同学们如果想了解它还有哪些有趣的性质,课后可以去看这本书——《斐波那契数列》,一定会有更多的收获。
评析:独立研究数列的性质,对于小学生来说是颇具挑战性的。在本教学环节中,教师充分地信任学生,为他们提供自由探究的时空,并適当给出一些探索的方向和思路,给学生提供攀登的脚手架。学生小组合作、自主发现、集体交流,找到了斐波那契数列很多神奇的性质。这些有趣的发现,让学生欲罢不能,让他们为数学之神奇着迷,让他们为自己的成就感到自豪。在这一高度抽象的纯数学的理性研究过程中,学生发现了如此之多的神奇而有趣的现象,这种趣味是一种发现的乐趣、求知的乐趣和充满知性的乐趣。最后推荐相关书籍,引导学生将研究延伸到课外,让课堂的影响更为深远。
三、明理得趣,品味数列
1.寻找生活中有趣的斐波那契数列现象
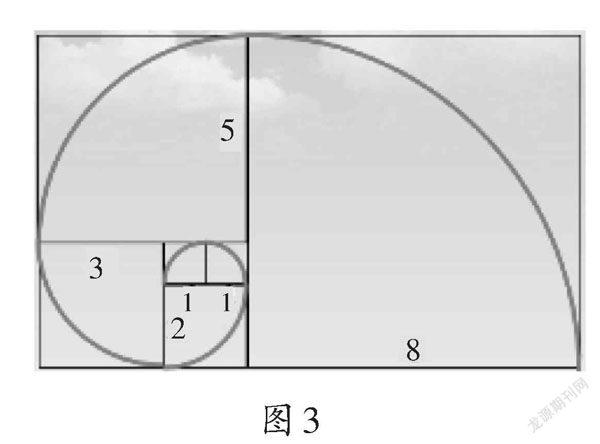
师(出示图3):除了兔子问题,生活中还有很多地方也藏着斐波那契数列,让我们一起来看看吧!海螺的壳上都有一条螺线,可以描绘成图3的样子。这个螺线图和斐波那契数列有什么关系呢?
生1:这些小正方形的边长就可以组成斐波那契数列。
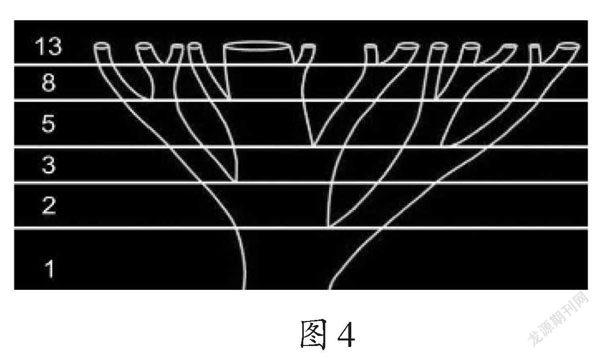
师:植物当中也有斐波那契数列。一些树枝的树丫数量蕴藏着斐波那契数列(如图4)。很多植物的种子排列中也涉及斐波那契数列。松果果实上的螺线顺时针有8条,逆时针有13条,这是什么数?
生2:是斐波那契数列中两个相邻的数。
2.感悟大自然中蕴藏的深刻哲理
师:植物如此进化是为了更好地利用空间,是一种优化的生存策略。
生3:大自然真是太神奇了!原来斐波那契数列就是大自然“发明”的呀!
师:正如古代大哲学家庄子所说:“天地有大美而不言……万物有成理而不说。” 从宇宙星辰到植物、动物都蕴藏了斐波那契数列(如图5)。看到这些,你有什么感受?
生4:天地之间蕴藏着无言的美和深刻的规律,数学世界也是如此。
生5:我们要敬畏大自然、保护大自然,还要去探索大自然无穷的奥秘。
3.欣赏艺术作品的数学之美
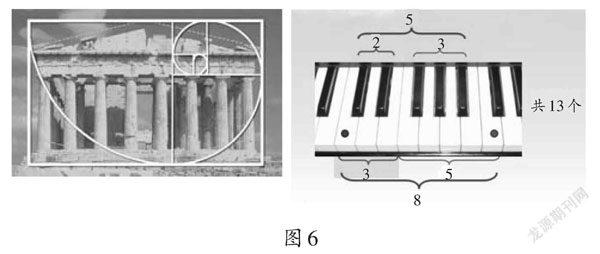
师(出示图6):很多画家、音乐家、建筑师也感受到了斐波那契数列的神奇,并把它应用到自己的艺术创作中。下面就让我们来欣赏一下吧。
生6:原来艺术里也藏着很多数学原理呢!
生7:斐波那契数列真是太美了!数学真是太美了!
评析:立德树人是教育的终极目标。本教学环节中,教师带领学生从数学走向生活,在自然现象中发现规律,感悟哲理;从数学走进艺术,在艺术世界中回味数学之美。学生感受到大自然神奇的力量,感悟到数学迷人的魅力,科学思维与人文素养相辅相生,互相滋养。这种超乎寻常的审美体验让学生的视野得到拓宽,认知得到震撼,心灵得到净化,在探索大自然的奥妙、品味斐波那契数列无穷韵味的过程中,获得了一种高品质的审美趣味。
四、理趣交融,拓展延伸
1.课堂小结
师:通过今天的学习,你有什么收获?
生1:我不仅知道了斐波那契数列是什么样的,还知道它是怎么来的,而且它有很多特别有趣的性质。
生2:原来大自然中就藏着很多斐波那契数列,大自然真是太美、太神奇了!还有难和易是相对的,是可以互相转化的。
师:斐波那契数列在计算机、生物、物理、金融等很多领域发挥着重大的作用。
2.课后思考
师:回到开头的比萨斜塔,它斜得这么厉害,能登得上去吗?(能)比萨斜塔的楼梯中也藏着斐波那契数列,你相信吗?
师(出示问题):上楼梯,每次可以上1级或2级,爬到第2级有几种方法?爬到第3级呢?第4、第5级呢?这些问题与斐波那契数列有什么关联呢? 留给同学们课后去思考。
评析:在趣理交融的课堂总结后,学生的成就感是非常强烈的,他们享受到了探索真理、洞察真相、品味艺术的乐趣。此时,教师趁热打铁,回到课始的情境,引领学生思考爬楼梯的问题。这样的设计能让学生带着问题走出课堂,将学习探究延伸到课外。如此,课堂边界被进一步拓宽,正可谓“课已终,思犹在,趣无穷”。
“理趣课堂”就是要让学生在探求真知的过程中获得智慧,体验成功,感受数学无穷的奥妙,产生持续学习的不竭动力,从而有效提升数学核心素养。
