精心设计前测 精准开展复习
2022-11-11陈春莺
陈春莺

[摘 要]在整理复习教学中,教师可以联系已经学过的知识设计前测练习,使学生能够迁移旧知、学习新知。通过前测练习,教师能了解学生的知识系统化水平,诊断学习过程与结果,同时审视自己的教学方法,从而提升复习的针对性和有效性,实现精准复习。
[关键词]前测练习;知识结构;精准复习
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2022)23-0032-03
传统整理复习课一般按“回顾知识—梳理沟通—巩固练习”的流程开展教学,教师没有事先了解学生的学习结果,不清楚学生的知识缺漏,课中“重点整理复习什么内容,怎么整理复习”成了笔糊涂账。基于以上考虑,笔者在复习课教学中精心设计前测练习,通过前测结果了解学生的学习成果,从而开展精准复习。下面,笔者结合借班教学“分数乘、除法整理复习”一课的体会,谈谈如何精心设计前测,为学生精准制订复习计划。
分数乘法、除法历来是学生的学习难点。教学中,为突破难点,部分教师会编顺口溜让学生强记:“已知单位‘1’用乘、未知单位‘1’用除,比单位‘1’多用1加,比单位‘1’少用1减。”奈何收效甚微,学生的错误率仍居高不下。因为借班教学更需要了解学生对知识的掌握情况、认知难点及知识结构的建立情况等,所以笔者设计以下教学环节。
一、精心设计前测练习,准确把握学情
教学新课时,通过开展课堂前测,教师能够很好地了解学生当前的知识水平和发展需要,从而精准施教。而在整理复习前,从单元或知识体系的视角出发设计前测练习,对教师准确把握学情、确定复习重难点同样重要。
1.利用前测练习,精准把握认知结构
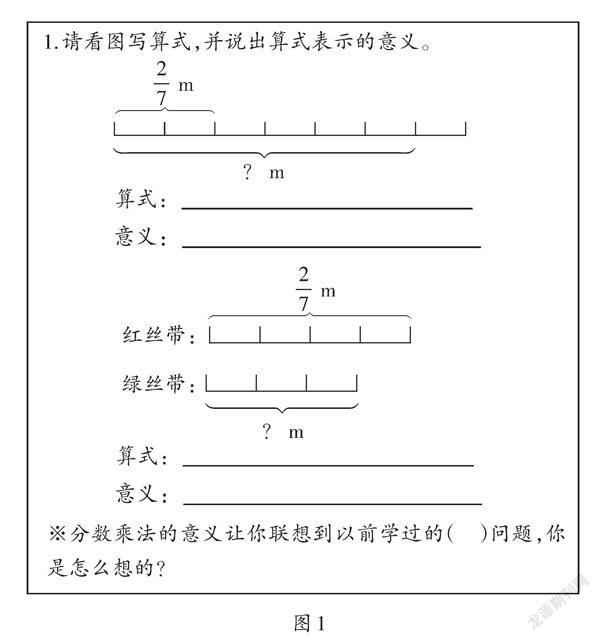
“注重对教学内容的整体把握”是课程实施的基本要求。知识体系具有上下贯通的特点,可以帮助学生纵向透视知识之间的联系,让学习知识和运用知识的效率大大提高。但实际教学中,部分教师缺乏知识系统化的意识,习惯把所有教学内容当成全新的知识来教学,费力又低效。其实,教师可以在前测练习中设计相关问题,借助大数据技术,精准把握学生的知识系统化水平。如分数乘法的意义有两层:一是求几个相同分数的和,二是求一个数的几分之几是多少。这样看,分数乘法的意义与“倍”的意义不谋而合。学生三年级初识“倍”,有几个几即这个数的几倍;五年级学习小数乘法,引入“小数倍”,具体事件中领会倍数可以是整数,也可以是小数,有时用小数倍表示两个数量间的关系更直观。同理,“用分数表示两个数的关系”可以理解为“表示两个数的分数倍”。基于此,笔者在前测中设置以下练习(如图1),先让学生说出各分数乘法算式的意义,继而提问:“分数乘法的意义让你联想到以前学过的( )问题,你是怎么想的?”考查学生是否在分数乘法问题与倍数问题之间建立了联系。在总复习阶段的前测练习中,还可以追问“分数乘、除法问题的解题方法还可以用来解决哪类问题?”,引导学生将分数乘、除法问题与比的问题、百分数问题建立起联系,进一步完善知识结构。
经统计,在完成了前测练习的近五十位学生中,仅三位学生将分数乘、除法问题与倍数问题建立起联系,少数几位学生能将其与小数乘法相联系,多数学生无从下手。由此笔者推测,该班原教师在教学分数乘、除法时没有联系旧知,导致学生在学习倍数知识的过程中积累的经验无法得到迁移。
数学知识间的联系往往是内隐的,这就要求教师教学时要重视对教学内容的整体分析,了解知识的结构与关联,提炼能打通知识间的联系、发挥核心作用的数学概念,由此构建起数学学习主题统整下脉络清晰、条理分明、相互联系的数学知识体系,使学生形成简化的、本质的、对未来学习更有支撑意义的、内在逻辑性较强的数学基础知识结构。
2.精心设计前测,反映教学方法和策略
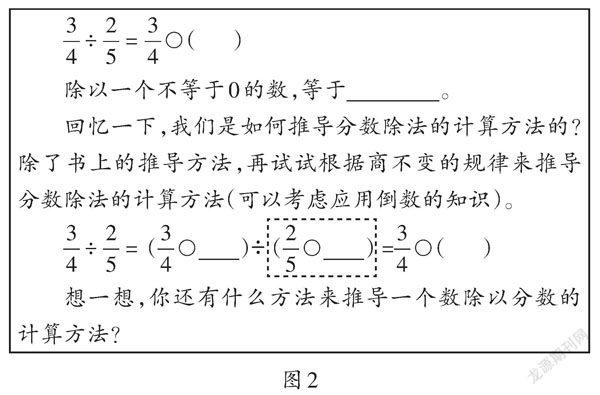
有效的复习前测有着反馈教学情况的作用,使师生都能了解自己存在的问题。如“一个数除以分数”的教学,人教版教材通过“2/3小时走了2千米,每小时走多少千米”这一问题,使学生理解算理。具体过程如下:分析出“因为2/3小时里有2个1/3小时,所以先求1/3小时走的路程,再求1小时走的路程,即2×1/2×3=2×(1/2×3),因此2÷2/3=2×3/2”,从而概括算法。该方法虽然具有普适性,但学生自己难以想到,而且推导过程较复杂,学生不易掌握。其实六年级学生已经有了丰富的转化经验,教师可以引导他们尝试把除数转化成整数,来推导分数除法的算法。笔者在前测中设计以下练习(如图2),引领学生自主推导。
除以一个不等于0的数,等于________ 。
回忆一下,我们是如何推导分数除法的计算方法的?除了书上的推导方法,再试试根据商不变的规律来推导分数除法的计算方法(可以考虑应用倒数的知识)。
虽然之前没有接触过该推导方法,但是多数学生仍能顺利完成前测,可见学生具备应用知识独立解决问题的能力。教学中,教师不应拘泥于教学教材内容,而应博采众长,采用多样化的策略帮助学生突破认知难点,同时通过“你还有什么方法”这类问题鼓励学生尝试独立解决问题,积累数学学习经验,培养不唯书、不唯上的探究精神。
3.精心设计前测,诊断学习过程与结果
有效的复习前测不仅能诊断出学习的结果,还能诊断出学习过程中的情感、策略等信息。学生是否已经熟练掌握判断单位“1”的方法?解答分数乘、除法问题的错误类型主要有哪些?产生的原因是什么?根据这些问题,笔者设计前测练习(如图3)。
以上练习目的明确,题1考查学生判断单位“1”、分析数量关系的能力;题2让学生选择信息和问题自主编题并解答,增强练习的综合性、开放性和灵活性,落实“四能”要求。由于借助了大数据,每個学生的答题结果都被详细记录下来。经统计,选择“②-A”组合的学生最多,共计18人,解答正确的有15人;其次是选择“①-B”组合的学生,共计15人,解答正确的有7人,不足一半;部分学生选择“③-A”“③-B”“④-B”组合,答对和答错的人数对半开,还有几位学生选择“①-C”和“④-D”的组合,他们都没解答出来。另有部分错误的组合,如信息与信息、问题与问题的组合,以及“④-C”这样“明知故问”的组合。
据此,笔者对该班教学情况做出判断:首先,在知识结构上,师生都缺少整体把握知识结构的意识;其次,在知识技能上,學生对于单位“1”已知的问题掌握较好,对于单位“1”未知的问题则掌握欠佳。
二、根据前测结果,精准复习
基于前测数据,教师得以准确把握学情,科学制订教学目标,合理安排教学任务,为学生精准制订复习计划。本课将围绕两个任务展开复习。
1.梳理知识,形成结构
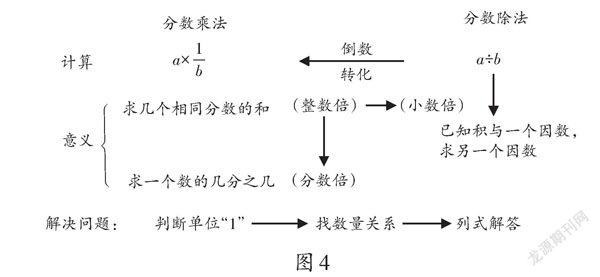
这两个单元结构相似,均由意义、计算、解决问题三大内容组成。复习时从计算开始梳理,借助倒数的知识与转化策略,使分数乘、除法计算成为有机整体。接着看图(如图1)提炼分数乘法的意义,沟通其与倍数问题的联系。上图中,2/7×3表示3个2/7连加,即2/7的3倍;下图中,2/7×3/4表示2/7的3/4是多少,即2/7的3/4倍。重点引导学生以红丝带为一倍数,明确当绿丝带的长度不到红丝带的一倍时,它们之间的倍数关系可以用分数倍表示,即绿丝带的长度是红丝带的3/4倍,这与小数倍(小数乘法的意义)、分数表示关系的意义一致。这样就把“分数、小数表示倍数关系的含义”纳入“自然数表示倍数关系的含义”这一已有的认知体系中。一旦两者之间建立联系,倍数问题的学习经验就可以迁移到分数乘法的学习中来,用“已知一倍数求几倍数用乘法(求几个几是多少);反之,用除法”的经验诠释“已知单位‘1’用乘法,未知单位‘1’用除法”的道理。解决稍复杂倍数问题的经验,也可以迁移到解决稍复杂的分数乘、除法问题中,如借助“和倍、差倍问题”的学习经验,来学习“求比一个数多(少)几分之几的数”以及“已知比一个数多(少)几分之几的数,求这个数”等问题,事半功倍。全课梳理板书如图4。
实际上,在整理复习阶段,沟通知识间的联系只是补救措施,教师应在新知教学时及早渗透,为后续学习做好必要的铺垫。如早在教学三年级“认识倍”的时候,就可以埋下“倍可以是整数倍,也可以不是整数倍”的伏笔;五年级教学小数乘法中有关“小数倍”的知识时,就可以引导学生推测“分数倍”的存在;教学分数意义的再认识时,帮助学生把“分数表示关系”的含义明确为“分数表示倍数关系”等。
2.查漏补缺,适度提升
梳理沟通,可以帮助学生实现知识体系的建构;而结合前测练习查漏补缺,则是帮助学生突破认知难点、提高学习水平的有效途径。本课中,师生利用图3前测练习“用分数乘、除法解决问题中的第2题”,有效打破学生解答单位“1”未知类问题错误率高这一困局。这道题中,备选信息①、②、③、④分别与已知信息“男工人比女工人多1/5”组合,共可在备选问题A、B、C、D的框架下提出12个有效问题。在该题组中,教师把讲解重心落在“①-B”组合上:某工厂中,男工人有330人(①),男工人比女工人多1/5,女工人有几人(B)?教师出示部分学生的不同解法——算术解法和方程解法,让学生比较异同点,引导他们发现两者的共同点都是先找到数量关系:女工人人数×(1+ 1/5)=男工人人数。方程解是顺向思考,所以用乘法解答,而算术解则需要逆向思考,所以用除法解答。这样,使学生进一步明确单位“1”未知的问题要用除法解答的道理。接着,笔者出示典型错例“330×(1- 1/5)=264(人)”,请学生分析原因。经过交流,学生发现错误原因是把题中“男工人比女工人多[1/5]”这一信息直接反向叙述为“女工人比男工人少1/5”,即错误是由“两个数量的多少关系可以反向叙述”这一经验的负迁移导致。学生经过进一步交流,得出分数乘、除法问题和倍数问题一样同时存在标准量和比较量,两者相互依存,变换标准量(一倍数或单位“1”),其倍数关系也相应改变。
在学生深挖错误根源、找准问题症结之后,教师随即安排后测练习,请学生从中选择单位“1”已知、未知的问题各一道来解答,要求尽量选择未解答过的问题。这里看似把选择权让给学生,降低练习难度,实则是在学生选择信息、提出问题、分析问题、解答问题的全过程中,对学生的“四能”发起新一轮挑战。同时,通过让学生根据能力选择难易程度不同的题目,实现“让不同的学生学习不同的数学”的目的。
总之,在整理复习教学中精心设计前测,可以准确把脉教学,实现精准复习。
