基于深度学习统领的教学新思考

尤海琼

［摘 要］随着课程改革的实施与推进，课堂教学也发生着深刻的变化，教学越发关注学生的发展需求，关注学生核心素养的发展。深度学习统领的单元教学能消除传统的以课时为单位的教学弊端，调整学生的碎片化学习状态，有效引导学生建构知识、技能与素养之间关联性、结构性的认知结构。文章以“分数的初步认识”单元为例，探讨如何基于深度学习理念开展单元教学内容的整合重构。

［关键词］分数的初步认识；深度学习；单元教学

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2022）23-0020-03

当前，由深度学习统领的单元教学正如火如荼地开展着。小学数学深度学习是学生在教师的引领下，围绕具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的数学学习过程。深度学习统领的单元教学是指教师以单元学习主题为主线，对学习内容的数学本质进行分析，对教学内容进行整体分析和适当重组。它突出单元学习主题的关键与重点问题，避免知识内容、学习方法的不必要重复；实现用少量主题的深度覆盖去替换学科领域中对所有主题的表面覆盖；为学生提供多元的学习素材，帮助学生打通知识到核心素养的通道。

在深度学习的统领下，如何从单元整体教学层面入手，调整原有的知识编排架构，对原有的教学内容进行必要的、合理的重构？下面就以人教版教材三年级上册“分数的初步认识”单元中的第一课时为例，进行教学内容重构与活动设计。

一、单元内容的教材编排的现状

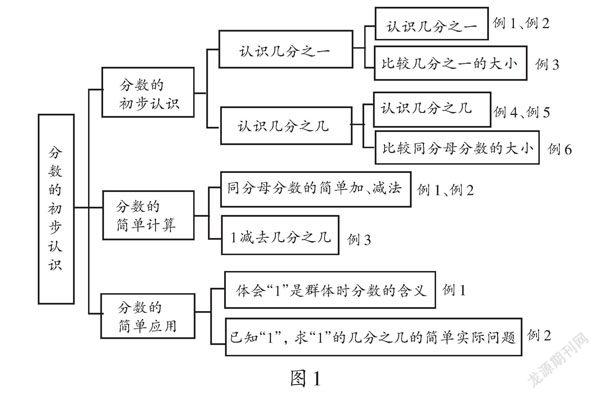
人教版教材三年级上册“分数的初步认识”的编排：

从整数到分数，本单元是对数的概念进行扩展。无论是在意义、读法、写法还是计算上，分数与整数都有很大的差异，是学生对数的认识的一次质的飞跃。从具体编排结构来说，本单元知识之间按内在联系可分为三部分：分数的初步认识，分数的简单计算，分数的简单应用。从教材编排的内容来看，部分课时的内容被分割，不利于学生高效率、整體化地学习分数。为促进学生整体学习分数知识，促进深度学习统领的单元教学，笔者对这一单元的教学内容进行重新规划。

二、单元内容重构的主导观念

1.从学情出发，制定教学目标

以学生的学情为依据，以核心素养发展为目标，遵循学生的认知规律，了解学生学习相关内容的基础、可能出现的问题以及发展需求，提炼学习内容所隐含的高阶思维和关键能力，制定教学目标。以此激活学生已有的经验，有效实现学生深度学习。

2.深度解读教材，厘清知识结构

在对教学内容进行整合重构时，需要全面分析教学内容，深入挖掘教材。教师要基于对教材的解读和教学目标的准确定位，把握数学核心知识，厘清知识结构。既不完全打破原有的教材逻辑框架，也不刻意打乱数学学科知识前后的连接顺序，而是基于对数学核心内容的整体分析，通过调整内容呈现的顺序和形式，拓展和补充学习资源，将教材呈现的内容设计成适合学生深度学习的素材。

3.聚焦学科本质，促进核心素养

张奠宙教授曾指出：数学教育自然是以数学内容为核心。一堂好的数学课，必然要凸显数学本质。深度学习统领下的单元整体教学，指向学生对内容本质、学科思想与方法的理解，指向应用所学知识和方法解决新问题的能力，突出学科本质，让学生在享受数学探究的乐趣中和构建新知的过程中发展高阶思维，促进数学核心素养的提升。

三、“分数的初步认识”单元教学内容重构后的规划

人教版教材三年级上册“分数的初步认识”教学重构：

课时1：通过操作活动使学生认识几分之一，继而学习几分之几，会读、写分数。

课时2：在巩固课时1的基础上学习比较同分子分数、同分母分数的大小。

课时3：会简单计算同分母分数的加、减法，掌握1减几分之几的算法及算理。

课时4：解决有关分数的简单实际问题。体会“1”是群体时分数的含义，会解决已知“1”，求“1”的几分之几的简单实际问题。

课时5：分数的应用。

四、对“分数的初步认识”单元第一课时重构的思考

本单元第一课时“分数的初步认识”是单元的起始课，也是学习分数的“种子”课。

1.整体入手，调整教学目标

在深度学习统领的单元教学的理念下，教学目标的设置要从整体入手。调整后的第一课时是将教材原先安排的课时1与课时2进行整合，去掉课时1和课时2关于分数大小的比较。将调整后的课时1的教学目标定位为：（1）结合具体情境在动手操作的过程中感受几分之一的形成，体会和理解几分之一的含义；（2）将对几分之一的理解迁移到几分之几的学习，会读、写分数，知道分数各部分的名称及意义；（3）感悟数形结合思想，完善数的概念，发展数感，体会分数在实际生活中的应用与价值。总的来说，这些目标包括知识、能力、情感与核心素养。调整教学目标之后，教学内容更整体化和科学化。

2.基于学情，把握教学起点

根据学情把握学生的认知起点，是帮助学生顺利进入新知学习的关键。它可以激发学生认知中的逻辑经验和现实经验，能够架起新旧知识之间的“桥梁”，更好地借助旧知识同化新知识。对“分数的初步认识”的学情分析有三方面：一是分析学生在分数的理解与认识上有什么特点；二是分析不同的学生在学习分数的过程中可能会遇到哪些困难；三是找出学生学习分数的前概念是什么。

笔者在分析了学生的学情后，了解到学生虽然在生活中听到过[12]、[13]等分数，但对于分数的含义是陌生的，也不清楚分数是从何而来。因此，笔者在导入分数环节做如下设计。

【教学片段1】

师（课件呈现：  ）：把4个蛋糕分给2个小朋友，怎么分比较公平？

生1：平均分。

师：把4个蛋糕平均分给2个小朋友，每人分到几个？

生2：2个。

（课件动态演示把4个蛋糕平均分给2个小朋友，每人得到2个）

师（课件呈现： ）：把1个月饼平均分给2个小朋友，每人分到几个？

生（齐）：半个。

师：你能用一个数来表示半个吗？

生3：0.5，1/2，……

师：是的，我们可以用小数0.5表示半个，也可以用分数1/2表示半个。今天这节课，我们就来认识分数。

通过“把4个蛋糕平均分给2个小朋友，怎么分比较公平？”引出学习分数的基础——平均分，接着利用“把1个月饼平均分给2个小朋友，每人分到几个？”把学生原有的认知“用整数表示平均分的结果”引到“用分数表示平均分的结果”，让学生感悟到，当一些数量用整数不能表示的时候，可以用分数表示。

3.沟通内容，梳理知识

数学中的很多知识点都不是孤立的。本单元学习的分数、之前已经学习的整数以及后续要学习的小数，都是“数家族”中的一员，如何把它们融合在一起以形成一个系统化的“数家族”，而不是一个一个独立的个体？可以借助数轴。

【教学片段2】

课件出示数轴：

师：这是一条数轴，我们学过的数都能在上面找到。想一想，1/2在这条数轴上的什么位置？

生1：在0和1之间。

师：具体在哪里？

生2：在0和1中间。

师：1/4在数轴的什么位置？

生3：在0和1/2中间。

师：那1/8在数轴的什么位置？……随着平均分的份数越来越多，分母越来越大，分数越来越——

生（齐）：小。

师：这个分数就越靠近——

生（齐）：0。

师：会等于0吗？

生（齐）：不会。

学生能轻易在数轴上找到整数1、2，因为这是学生已经学过的知识。在此基础上，让学生在这条数轴上找今天学习的分数1/2、1/8。学生在数轴上找整数、分数的过程中，感悟到分数和整数一样能在数轴上找到，分数跟整数一样是“数家族”中的一员，从而对分数的认识更加丰满。

4.聚焦本质，促进迁移

深度学习的过程应当着眼于学生对所学内容的整体理解，促进学生的知识建构和方法迁移。因此，教师要善于把前后知识有机地联系起来，培養学生的迁移能力，促进学生高阶思维的发展。

【教学片段3】

师：刚才我们找到了一个月饼的1/2，试着创造一个几分之一的分数。

生1：1/3、1/4、1/10……

师：拿出图形，涂一涂、想一想，涂色部分是整个图形的几分之一？说说你的做法。

生2：我表示的是1/3。我把长方形平均分成3份，涂色部分是其中的1份，也就是它的[13]。

当学生学习了“1/2”后，“要求学生动手涂一涂，表示几分之一的分数”的环节是学生将对分数“1/2”的学习迁移到对几分之一分数的探究。

【教学片段4】

师（出示，再涂一格）：涂色部分是整个长方形的几分之几呢？说说你的想法。

生1：涂色部分是长方形的2/4，因为把一个长方形平均分成4份，2份是它的2/4。

师（再涂一格）：现在涂色部分是整个长方形的几分之几呢？

生2：涂色部分是整个长方形的3/4，因为把一个长方形平均分成4份，3份是它的3/4。

师（继续涂）：现在涂色部分又是多少呢？

生3：涂色部分是长方形的4/4，也就是整个图形。

师：真聪明，涂色部分是长方形的4/4，也就是1。

当学生完成对几分之一分数的探究后，教师动态演示涂格子的过程，并提问：“涂色部分是整个长方形的几分之几？”基于前期对“1/2”和几分之一的认识，学生对于分数的认识已经非常清晰，此时，学生就能自然而然地将经验迁移到对几分之几的探究，学起来得心应手。学生在“借助已知解决新知”的过程中感受到利用迁移获取新知识的快感，自然就增强对学习数学的信心与兴趣，形成探究精神。

总之，深度学习统领的单元教学要求教师在开展教学时始终带着这几个问题：学生学习这个知识的起点在哪里？与这个知识相关的内容有哪些？学生在学习的过程中可能遇到哪些困难？在完成教学内容的同时，学生的核心素养发展如何落实？唯有清楚回答了这几个问题，才能真正引领学生完成从知识到核心素养的自我实现。