基于层次分析法的南极磷虾瞄准捕捞网口路径规划

姚宇青，戴 阳，王鲁民，王书献，3，陈 帅，杨胜龙，石永闯

（1.上海海洋大学信息学院，上海 201306；2.中国水产科学研究院东海水产研究所，农业农村部渔业遥感重点实验室，上海 200090；3.大连海洋大学航海与船舶工程学院，辽宁大连 116023）

南极磷虾是高度集群的一类浮游生物，富含优质蛋白质，可以用作食品添加剂、动物饲料、饵食等，去壳的虾仁也可以直接食用，具有极高的经济价值和食用价值［1-5］。同时，南极磷虾油也具有很高的医学价值，能够增强人的免疫力、预防老年人的心脑血管疾病等［6-7］。目前南极磷虾捕捞技术主要包括传统拖网、连续捕捞系统、泵吸清空网囊技术和桁架拖网等4种。迄今为止磷虾捕捞深度的确定还完全依赖人工观察探鱼仪影像，如果探鱼仪发现前方有磷虾群，需要船长做出实时的反应，规划网口前进路线，以便通过磷虾群高密度区域捕捞更多的磷虾。这个过程具有很强的主观性和滞后性，容易错过捕捞的最佳时机，很难实现精准捕捞［8-12］，并且对于连续捕捞系统而言，一旦确定捕捞深度以后，就不再调整网口所在水层，若磷虾处在其他水层将无法捕捞。但是目前鲜见关于拖网作业前期对南极磷虾拖网网口路径规划的相关研究，亟待开发一种高效智能的磷虾捕捞网口路径规划的算法，在发现磷虾群时能及时、高效的规划好网口的前进路线，实现捕捞效益的最大化。

由于典型的路径规划方法，如基于人工势场法［13-14］、先进的智能算法如蚁群算法［15］、模拟退火算法［16］等，获得的路线都是曲率不连续的折线段，无法满足磷虾实际的网口路径规划任务要求。而基于样条曲线的规划方法，如Bezierspline、B-spline等［17-18］，以及基于直线与弧线拼接的规划方法，如Clothoid、Dubins等［19-20］，生成的路线往往需要先通过采样，得到路径点序列集合，将不同的路径点序列与不同的预设目标结合，通过连接会得到多条不同的路径［21］，从中筛选出最优路径。然而，现有候选集择优体系大多是基于单一赋权法［22］，单一赋权法指标计算包含主观和客观两部分，会导致权重偏好、鲁棒性较差等问题。层次分析法（analytic hierarchy process，AHP）是一种解决多任务、多目标的复杂工程问题的定性与定量相结合的决策分析方法。AHP将影响决策的因素两两对比得到相对重要的权重数值，通过权重得出各方案的优劣程度，能系统化、层次化的推荐最优的决策方案，在分险评估、资源分配、方案选择等多方面具有广泛的应用。葛声等［23］、朱振强等［24］使用AHP对无人机航路规划进行了改进，结果表明，AHP的应用具有良好的稳定性、实时性、合理性。

本研究在网口前进路线择优中引入层次分析法策略，实现主客观指标的量化表达，综合评价候选路径的最优性，在一定程度上克服单一赋权法存在的权重偏好、鲁棒性较差等缺陷。首先利用滑窗统计算法分析磷虾虾群体积反向散射强度，获取磷虾局部的密度中心位置坐标序列，构建基于3次B样条曲线的路径簇，在筛选最优路径时，使用层次分析法，将定性分析转化为定量分析，减少主观判断失误导致的捕捞量减少。最后，本文结合真实南极磷虾捕捞场景的实验数据对所提出算法的有效性与实时性进行了验证，以期对实现南极磷虾的精准捕捞提供帮助。

1 材料与方法

1.1 实验数据

数据来源：实验数据的采集设备为水声学仪器EK80科学回声探测仪（KONGSBERG，挪威），数据调查时间为2016年4月18日18∶12∶14到2016年4月18日18∶31∶53，调查范围为63°16＇46″S～63°18＇31″S、58°24＇26″W～58°30＇19″W。仿真平台为Windows10操作系统，MATLAB2018b（64位）。

采集的回波映像数据中除了磷虾集群信号以外，还包含了大量的高于磷虾回波强度和低于或接近磷虾回波强度的强干扰信号和弱干扰信号。本文将没有干扰信号影响时，采集的磷虾虾群体积反向散射强度（Sv，dB）的最大值和最小值作为消除干扰信号的上限阈值和下限阈值［25-26］。消除后的干扰信号点赋值为-999 dB。通过Echoview软件（V8.0.92）初步分析得出磷虾群分布水深范围为15 m到40 m，磷虾Sv数据目标强度最大值为-70 dB，最小值为-80 dB。图1为去除干扰信号后的磷虾集群散点图。

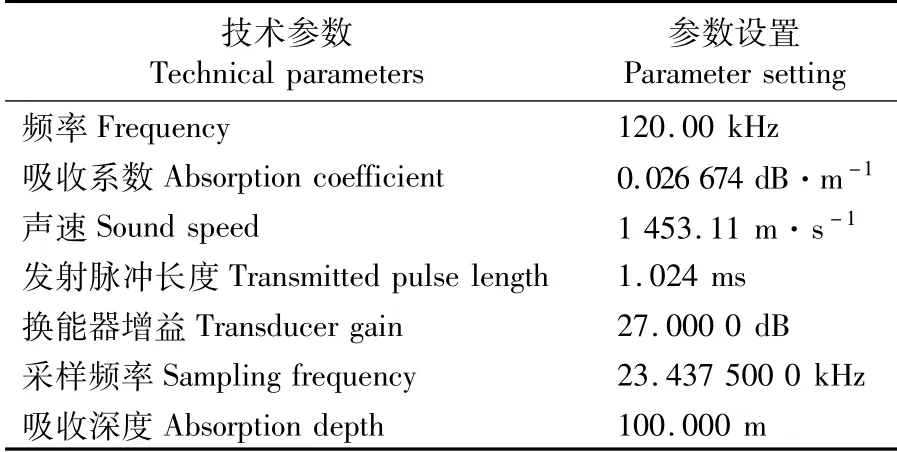
表1 EK 80数据采集系统参数Tab.1 Data acquisition system parameters of EK 80

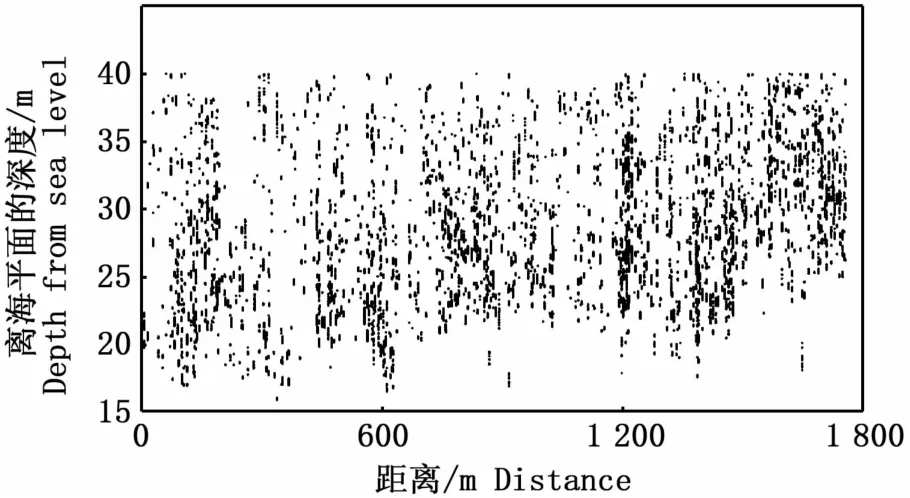
图1 去除干扰信号后的磷虾集群散点图Fig.1 Scatter diagram of krill colony after removing interference signal

1.2 路径规划

本文设计的磷虾捕捞路径规划主要包括两个部分：路径点选择和路径曲线构造。路径点选择的基本要求是目标点为窗口范围内密度最大点，即该点邻域内包含的点数最多，从而使得当网口通过该点时捕捞的磷虾最多。路径曲线构造的目的是将路径点序列平滑的连接，便于控制网口通过或尽可能接近这些点。

1.2.1 路径点选择

由于磷虾虾群体积反向散射强度与虾群生物数量有强相关性［27］，Sv数据图像能够很好的反映磷虾群的密度分布。本文通过分析Sv数据图像，设计出一种基于滑窗统计的方法从Sv数据中获取磷虾局部密度中心位置坐标。

滑窗统计方法需要设计一个矩形数据窗口，通过计算确定磷虾局部密度中心位置坐标在窗口中的具体位置。矩形数据窗口用于模拟人工观察鱼探仪图像，不同的是人工观察鱼探仪图像是根据颜色的深浅判断磷虾的聚集水层，会有一定的主观误差和滞后性，矩形数据窗口是通过统计符合磷虾目标强度的点的数量比较各个水层“目标资源量”的多少，找到磷虾的聚集水层，较人工的方式更加准确快速。具体实施步骤为：

Step1：构造一个P×L的数据窗（P为Sv原始数据行数，L为3到7的数，每次操作L的值取一个）；

Step2：计算窗内每行数据和，结果存放到矩阵B（P×1），矩阵B（P×1）最大的数所在的行即为该段候选磷虾密度中心的深度（路径点的纵坐标）；

Step3：计算该段深度下网口范围内最大和所在的列即为路径点的横坐标；

Step4：数据窗每次横向移动L个数据，直到结束，获得在L下的密度中心位置坐标序列。修改L的值，重复操作可以获得不同密度中心位置坐标序列。

图2为基于滑窗统计方法的路径点选择示意图。为了避免出现网口通过无磷虾区域，在计算控制点的纵坐标时，本文还考虑了磷虾群分布的水深范围。

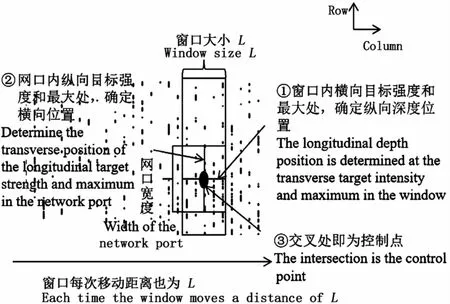
图2 基于滑窗统计方法的路径点选择示意图Fig.2 Schematic diagram of path point selection based on sliding w indow statisticalmethod

1.2.2 路径曲线构造

本节使用滑窗统计方法获得的路径点（下文的控制点同义）位置坐标，构造候选路径簇。为了使网口捕捞路线轨迹具有可执行性，同时降低计算难度，本文以3次B样条曲线为路径规划器，设计了一种高实时性的连续规划算法。

B样条曲线由控制点｛di｝i∈［1，M］组成，M为控制点总数。其中，｛fk（s）｝k＝［0，3］是3次B样条曲线的基函数［28-29］，定义为：

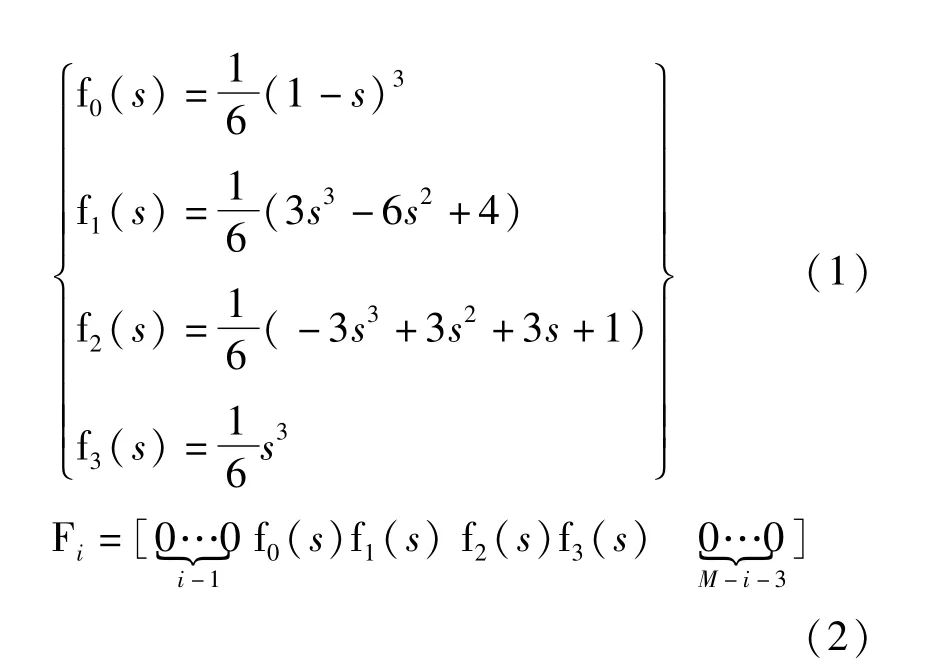
于是，3次B样条曲线的方程为：

平面轨迹表达式：

式（1）～式（4）中，s∈［0，1］为从初始状态到目标状态的归一化路径长度，i为控制点序号，表示第几个控制点，m为每段曲线所需的控制点个数，3次B样条曲线每段需要4个控制点，故m＝4。

但是，磷虾捕捞是一种实时作业方式，探鱼仪每次只能获得一段磷虾虾群的体积反向散射强度数据，上述的B样条曲线算法中，相邻两条3次均匀B样条曲线在衔接处只能达到零阶连续，并且对计算机硬件的运算和存储能力要求较高，这不利于降低捕捞成本。同时，当获得新的数据时，无法保证相邻的两条B样条曲线的光滑连接，导致网口在相接处无法沿着路线前进，进而影响对虾群的捕捞。

为了解决这个问题，本文采用了B样条曲线重叠拼接法［30］。为了保证路线之间衔接的平滑，重复使用上一段数据的控制点。

通过B样条曲线重叠拼接法，可以实现一边获取数据，一边进行路径规划，极大地提高了路线规划的实时性和有效性。

1.3 路径择优

在选择最佳网口前进路径时，为了使生成的网口捕捞轨迹尽可能涵盖收益最大化，同时，结合多目标（经济性、可控性）需求，本文采用AHP对可行捕捞轨迹进行评估，以筛选出最优的轨迹。

1.3.1 择优体系

基于AHP构建路径择优体系，路径优劣的评价指标包括捕捞率、路径长度、拐点个数、平均曲率。

1）捕捞率定义为：规划路径下网口移动路线覆盖范围C与磷虾群整体范围B的比率η，为了提高经济效益，捕捞率的值在合理范围内越大越好。计算方法为：

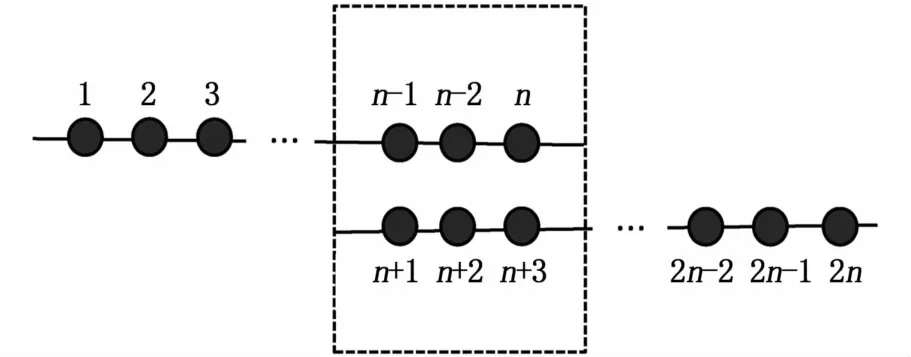
图3 重叠拼接法示意图Fig.3 Schematic diagram of overlapping splicing method

2）路径长度S是网口的移动距离。为了提高捕捞速度，降低路线跟踪难度，路径长度的值尽可能的越小越好。计算方法为：

式（6）中，sj为当前节点相对上一节点的长度增量，M为路径节点总数，j为第几个节点。

3）拐点指改变曲线向上或向下方向的点，拐点个数G反映网口控制的复杂程度，拐点个数越少控制越简单。判定方式为：如果Yj＜Yj+1且Yj＜Yj-1或者Yj＞Yj+1且Yj＞Yj-1，则G＝G+1。其中，Y为3次B样条曲线上点的纵坐标，G为拐点个数。

4）曲率和反映路径曲线的弯曲程度。由于滑窗统计方法窗口大小不一样时，节点数也不同，相互比较时会出现偏差，因此这里用曲率和与节点数之比，即平均曲率，反映路径曲线的弯曲程度。计算方法为：

式（7）中，Kj为节点j处的曲率，M为节点总数。

结合以上指标，基于AHP设计了自上而下的路径择优体系如图4所示。指标体系分为目标层、准则层、子准则层和方案层。

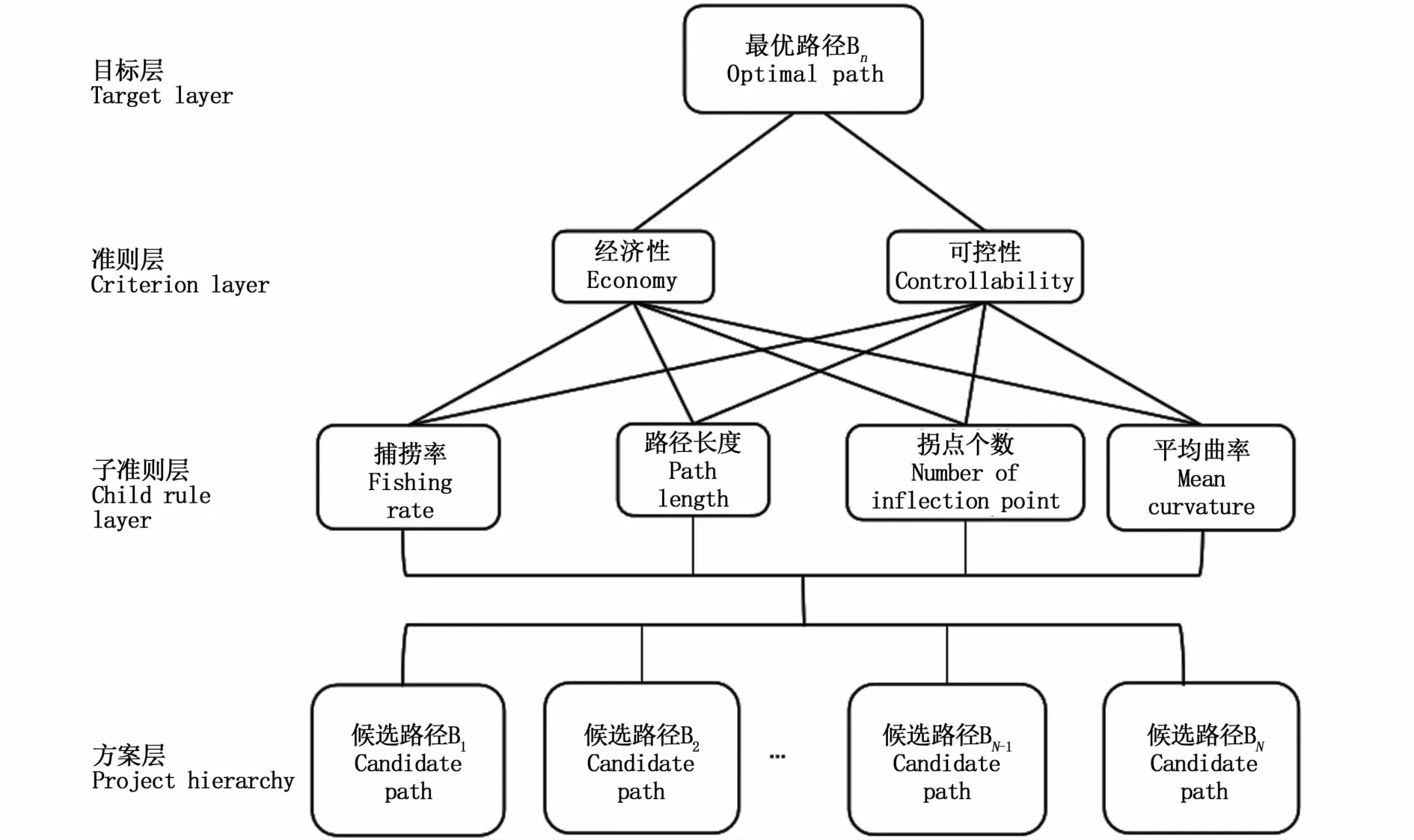
图4 层次分析模型Fig 4 Analytic hierarchy model

首先构造成对比较矩阵，将不同指标两两比较的相对重要程度定量表示。构造判断矩阵是AHP将研究问题从定性分析转为定量分析的关键步骤。采用1～9及其倒数评定每个因子的重要性，数值越大代表某个因子相比于另一个越重要，这两个因子之间的重要性为倒数关系。如式（8）所示［31］。

式（8）中，R为判断矩阵，n为子准则层因子的数量，aij为子准则层对应的任意两个因子对准则层的相对重要程度，且

其次，计算出R的特征值和特征向量，通过特征值法计算各个因子对应的权重。

式（9）中，RX为各个因子对应的权重，λmax为判断矩阵R的最大特征值，X为最大特征值λmax对应的特征向量。

这一步还需要通过计算一致性比例CR检验判断矩阵的一致性，若CR＜0.10，则判断矩阵通过一致性检验，可以直接计算权重，否则需要调整判断矩阵后才可以计算权重。CR计算方式为：

其中一致性指标CI的定义为：

式（11）中，N为判断矩阵的阶数。RI为平均随机一致性指标［32］，需查表才能得到。本文使用T.L.Satty计算的值，其值如表2所示，表中矩阵阶数为判断矩阵的阶数。

表2 平均随机一致性指标RITab.2 Average random consistency index of RI

判断矩阵通过一致性检验以后，所求的最大特征值对应的特征向量即为所得出指标的相对重要程度。

最后，计算层次总排序权重。计算方式为：

式（12）中，b1和b2为层次单排序中准则层对应的经济性和可控性的权重，C1j为层次单排序中子准则层的捕捞率、路径长度、拐点个数、平均曲率对应经济性的权重，C2j为层次单排序中子准则层的捕捞率、路径长度、拐点个数、平均曲率对应可控性的权重。

然后通过分析处理，得到各指标因子的得分数据，利用叠加分析将各个得分数据进行加权叠加，如式（13）所示：

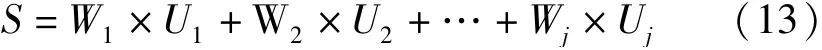
式（13）中，S为评价分值，Wj为第j项指标因子的权重，Uj为第j项指标因子的等级得分。指标因子的等级得分根据捕捞率、路径长度、拐点个数、平均曲率各自的排名得出，除了捕捞率都是数值越大得分越低。最后S最大的为推荐网口行进路线。

1.3.2 层次单排序和一致性校验

路径规划主要考虑经济性和可控性两个方面，路径规划的目的是提高经济效益的同时兼顾网口的前进路线易于跟踪控制，因此经济性和可控性两者重要程度之比为b1∶b2＝0.75∶0.25。考虑到评价指标对捕获路径筛选影响较大，只有选取代表性的指标才能降低模型的不确定性。本文通过调研大量文献［11，23-24，31，34］和咨询相关专家的建议，通过特尔斐法［33］完成了子准则层对准则层的判断矩阵构建。

首先，构建对可控性的判断矩阵。平均曲率影响网口深度变化的快慢，拐点个数影响网口深度调节的次数，因此这两种因素对可控性的影响较大。捕捞率和路径长度对可控性的影响较小。捕捞率、路径长度、平均曲率、拐点个数对可控性的影响程度关系为：平均曲率＞拐点个数＞捕捞率＞路径长度。其次，构建对经济性的判断矩阵。捕捞率直接影响渔获量的多少，是捕捞收益的决定因素，因此捕捞率对经济性的影响程度最大，捕捞率、路径长度、平均曲率、拐点个数对经济性的影响程度关系为：捕捞率＞路径长度＞平均曲率＞拐点个数。

子准则层对可控性和经济性的成对比较矩阵及权重向量如表3所示。

1.3.3 层次总排序和一致性校验

根据式（12）和表3的数据，计算层次总排序的权重，结果如表4所示。

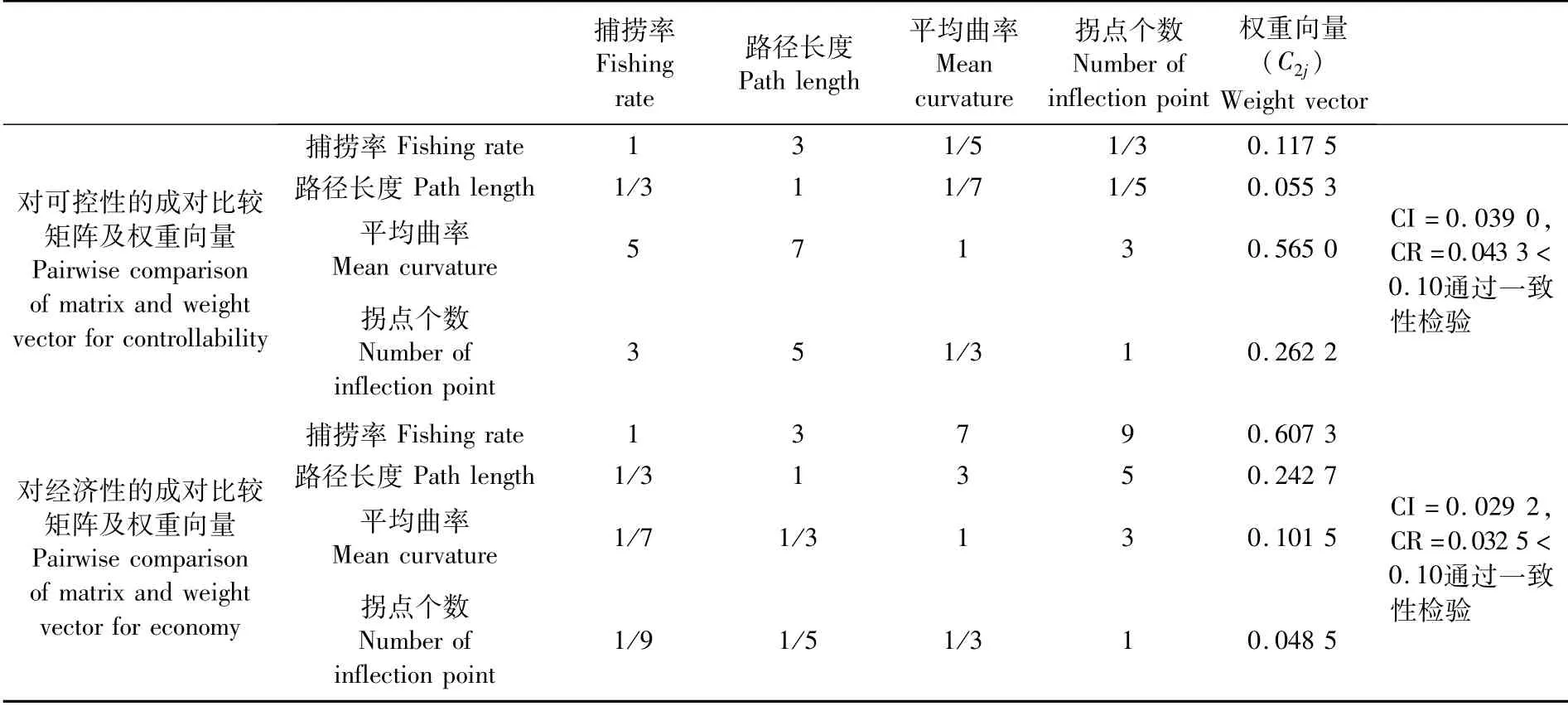
表3 成对比较矩阵及权重向量Tab.3 Pairw ise com parison ofmatrices and weight vectors

表4 层次总排序权重Tab.4 Total ranking weights of the hierarchy

层次总排序一致性检验：

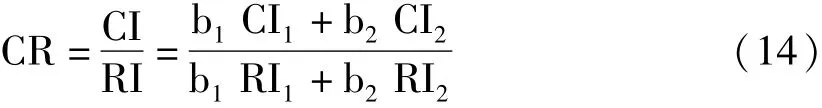
式（14）中，CI1和CI2，RI1和RI2分别为经济性b1和可控性b2对应的子准则层一致性指标和随机一致性指标。b1＝0.75，b2＝0.25，CI1＝0.029 2，CI2＝0.039 0，RI1＝0.9，RI2＝0.9。CI＝0.031 7，CR＝0.035 2＜0.10通过一致性检验，由此可知择优体系设计是合理的。

最终将捕捞率、路径长度、平均曲率、拐点个数的权重（表4）代入式（13），得到评价分值S计算公式为：

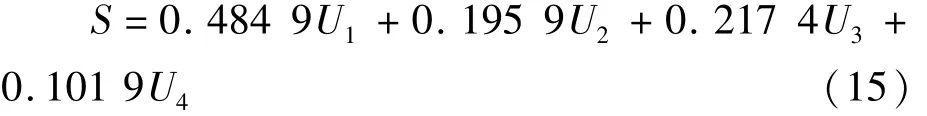
在评价路线时，将捕捞率U1、路径长度U2、平均曲率U3、拐点个数U4的得分代入式（15），S值最大的即为推荐的网口前进路线。

每条路线对应一组捕捞率、路径长度、平均曲率、拐点个数的数值。将所有路线的捕捞率、路径长度、平均曲率和拐点个数放在一起分别进行排名。根据排名的结果确定每条路线的捕捞率、路径长度、平均曲率和拐点个数所得的分值。数值大小相同的在同一个等级，得分也相同，相邻的两个等级相差10分。有多少个不同的数就有多少个等级。

由于无法保证捕捞率、路径长度、平均曲率、拐点个数数值大小分布相同，所以各自的等级总数或有所不同，最大得分也会有差异。为了减少差异对得分结果的影响，对等级总数不同的得分，采用min-max标准化（min-max normalization）进行处理。

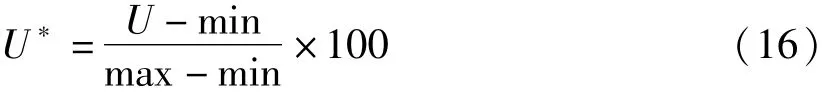
式（16）中，U表示捕捞率、路径长度、平均曲率、拐点个数未经标准化的得分，max、min分别表示捕捞率、路径长度、平均曲率、拐点个数的组内最高得分和最低得分，U*表示经过标准化处理以后的得分。

2 结果与讨论

本文规划路线的深度为网口中心位置离海平面的距离，由于磷虾群垂直分布范围有限，为了避免出现网口通过无磷虾区域，在计算控制点的纵坐标时，需要对网口的移动范围进行限制。例如本例中磷虾群分布水深范围为15～40 m，网口高度为20 m，当使用滑窗法获得的纵坐标小于25或者大于30时，纵坐标取固定值27.5。由得到的控制点坐标代入式（4）构造3次B样条曲线。图5-A～E展示了5种不同窗口大小下规划的网口捕捞前进路线。

图5-A～E规划的路线看起来在拐点处比较尖锐，这是由于横纵坐标数值相差较大引起的视觉差异。为此将图5-A规划的路径曲线进行了局部放大，如图6所示。

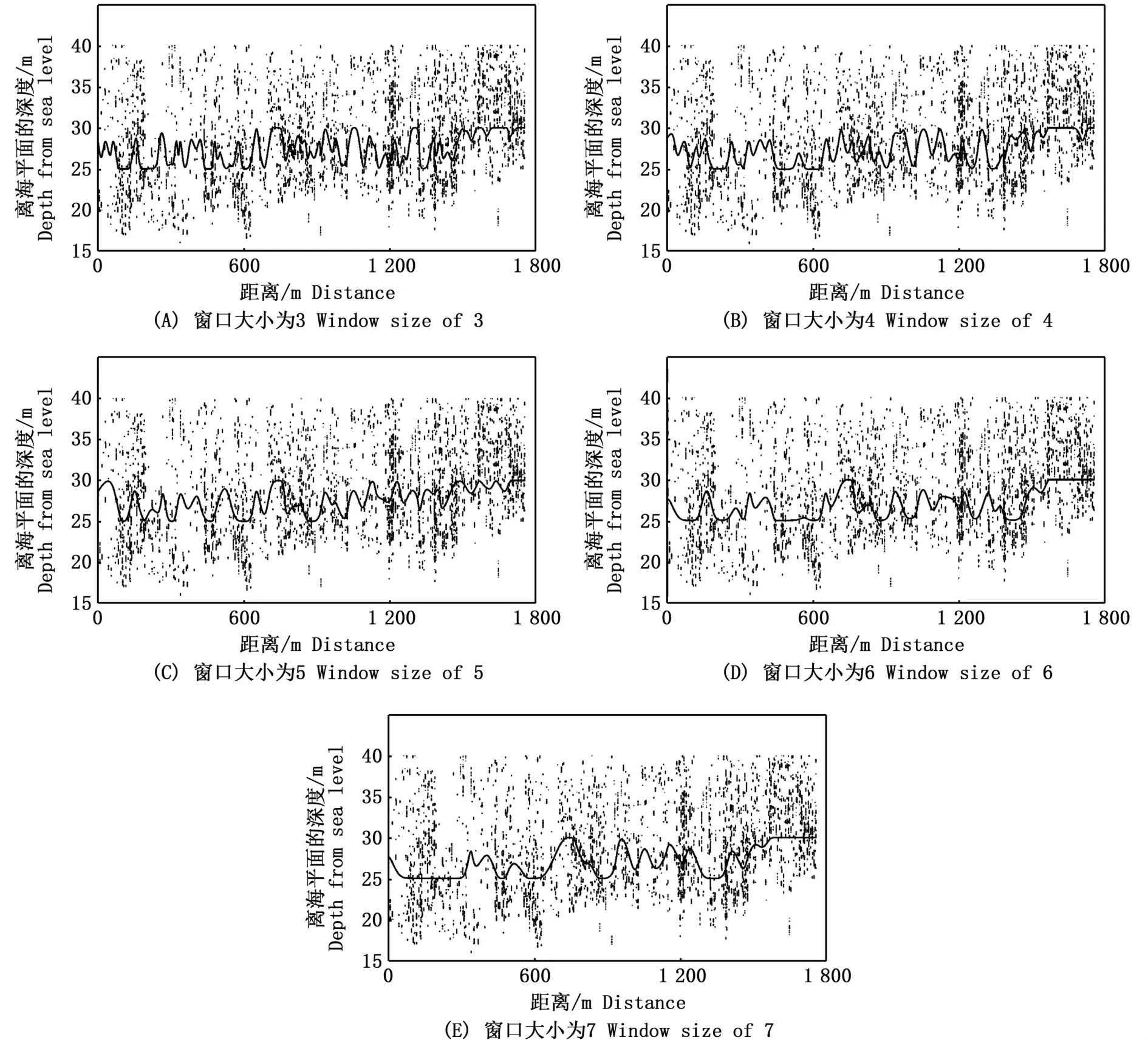
图5 规划的路径曲线Fig.5 Planned path curve

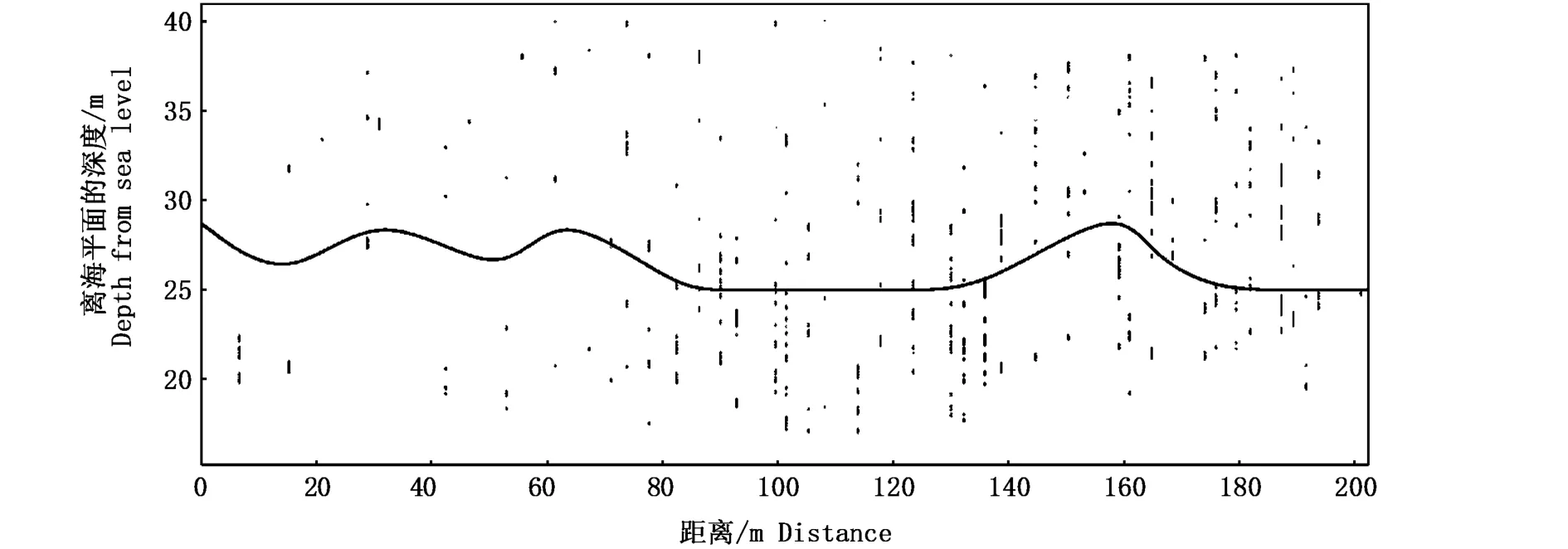
图6 图5-A的0～200 m范围的真实路径图Fig.6 Figure 5-A show ing the real path in the range of 0-200 m

分别计算以上5种窗口大小下路径曲线的捕捞率、路径长度、平均曲率以及拐点个数4个因子的数值，并对其大小进行排序，除了捕捞率以外，其他3个因子均为数值越大得分越低。将得到的分值数据代入式（15）的评价分值S计算公式，对图5-A～E规划的路径曲线进行了综合评价，综合评价结果如表5所示。

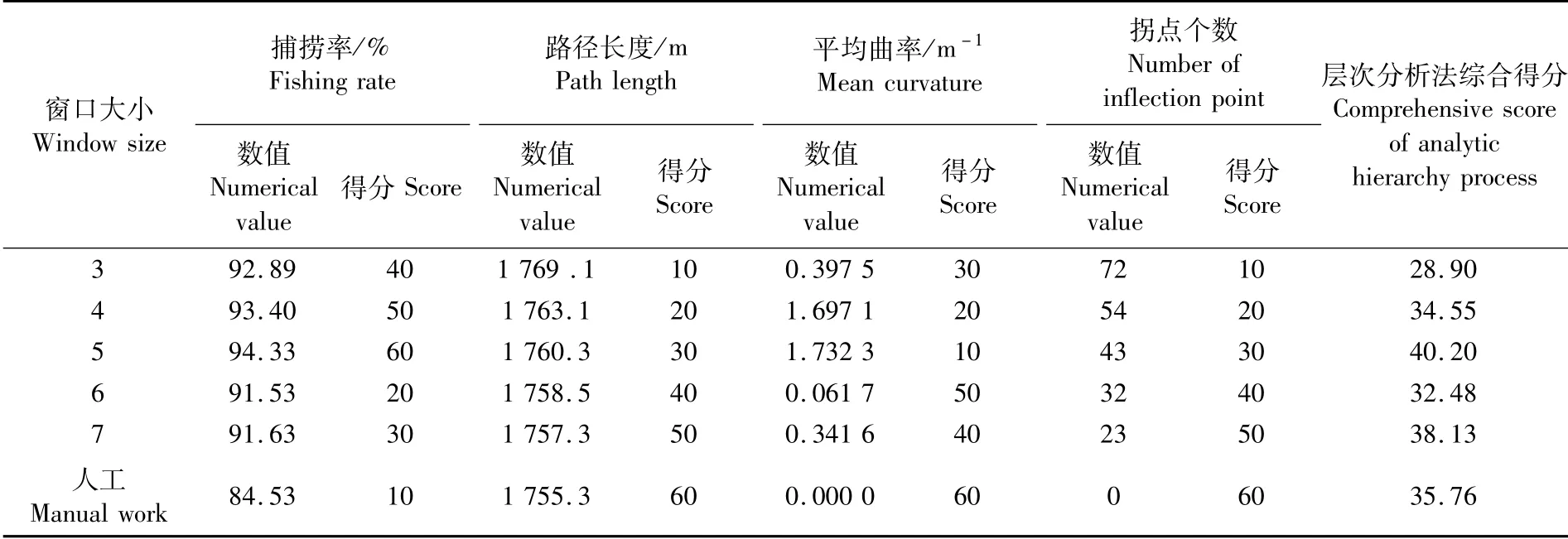
表5 各因子计算结果、等级得分（最高60分）及综合评价分值Tab.5 Calculation results of each factor，grade score（up to 60 points）and comprehensive evaluation score

根据层次分析法的综合评价得分，数据窗口大小为5时规划的路径曲线便是筛选出的最优路线。该条路径全长1 760.3 m，沿着路径前进时需要调整网口方向43次，平均每行驶41 m调整网口深度一次，捕捞率为94.33%。比人工方式规划路线的捕捞率多了9.80%，既易于控制船速和网纲长度使网口沿着该路线前进，捕捞率又高。本文在实验数据下多次重复实验，规划路径平均耗时为2.5 s，可以满足磷虾捕捞网口前进路线实时规划的要求，能够实时提供最优网口前进路线建议，说明本算法具有较高实时性与实用性。

3 小结

本文基于层次分析法设计了南极磷虾捕捞网口路线择优体系，通过分析磷虾体积反向散射强度，获得磷虾集群最大密度的深度分布数据，据此实时规划调节网口深度的前进路线，在有效降低人工规划路线的主观性和滞后性的同时，提高捕捞效率，降低人工成本。本研究通过在桁杆上安装升降板对网口深度进行微调，实现瞄准捕捞。该方法还可以扩展到其他鱼类的捕捞上，提高捕捞领域的自动化水平。

在路径筛选算法的选择上，本文采用了主观和客观相结合的层次分析法作为路径评价方法。在构造层次分析法判断矩阵时，由于客观事物的复杂性和人们主观判断的片面性和不稳定性，判断者只能给出一个近似的aij值，由于RI的计算需要生成随机的判断矩阵，导致每次的计算结果不尽相同，RI的值会有一定的上下浮动［32］，所以本研究使用了大多数学者使用的Saaty给出的RI值检验判断矩阵的一致性。在路径平滑算法的选择上，考虑到实时规划、桁杆速率和加速率不断变化等的要求，采用了Gordon等人通过拓展Bézier曲线，用B样条基函数替换了伯恩斯坦基函数的方式，构造的B样条曲线。该曲线的外形由对应的顶点直接控制的，改变一个顶点仅会对该顶点所处位置的前、后3段曲线的形状产生影响，这一特性恰好可以满足桁杆路径规划的要求，同时产生出来的曲线也较为平滑。仿真实验的结果表明层次分析法和B样条曲线在本研究中具有较高的适用性。

另外由于本研究缺乏完整、权威的磷虾水声学目标强度范围数据，现阶段的实际应用还需要与船员的经验相结合，以确定磷虾的目标强度范围，具体的捕捞情况还有待海上实验的验证。