基于IEKF的SINS/USBL组合导航系统安装偏差标定算法

徐 博，赵晓伟，王连钊

（1.哈尔滨工程大学 智能科学与工程学院，哈尔滨 150001；2.近地面探测技术重点实验室，无锡 214035）

海洋中蕴藏着丰富的战略资源，水下自主潜航器（Autonomous Underwater Vehicle,AUV）具有高度自主性、便携性和隐蔽性，目前广泛应用于海洋资源开发和水下目标探测等工作中[1]。捷联惯性导航和超短基线组合导航系统可为水下潜航器在水下工作提供姿态、速度和位置信息，但由于捷联惯性导航系统（Strapdown Inertial Navigation System,SINS）和超短基线（Ultra-short Baseline,USBL）设备存在安装偏差，如果不加以补偿将会影响组合导航精度，1 °的航向安装偏差角将会造成约1.7%斜距的位置误差，如果航向安装偏差大将会危及水下潜航器的航行安全[2]。安装偏差标定技术是SINS/USBL组合导航系统关键技术之一，标定精度的好坏直接影响到组合导航解算的精度。近年来，国内外很多机构学者围绕着SINS/USBL组合导航系统的标定开展了大量的研究。法国iXBlue、挪威Kongsberg、英国Sonardyne、美国LinkQuest等公司均有商用的深水超短基线定位系统，其中英国Sonardyne公司的Ranger2 Pro定位性能指标已达到0.1%斜距，这些公司均有针对自己设备的标定方案，一般是采用“8”字形标定轨迹，但有关标定算法的文献资料却很少。国内张涛等提出了一种基于小角度近似的安装偏差标定方法，首先对安装偏差角对应的姿态矩阵进行小角度近似，然后利用最小二乘算法对安装偏差进行标定。该方法简单易行，计算量小，但由于对矩阵进行了近似，所以会带来原理性误差，特别是当安装偏差角较大时会带来较大的标定误差[3]。在此基础上，赵俊波等对最小二乘标定算法进行了改进，同时提出了基于带约束的最小二乘标定算法，该算法具有一定的抗声速测量误差的能力[4]。童金武等提出了一种基于单应答器双矢量重构的安装偏差标定算法，该算法可以有效避免安装偏差的标定值收敛于伪点，为确定SINS/USBL组合系统安装偏差提供了新的理论依据[5]。王健等提出了一种基于相对量测信息滤波估计的安装偏差标定算法，将Huber M估计与变分贝叶斯相结合，有效解决了野值噪声对标定的影响[6]。徐晓苏等为了进一步提高SINS/USBL组合系统安装偏差标定的效率，同时增强标定方法的适应性，提出了一种交互多模型和无迹卡尔曼滤波器（IMM-UKF）辅助INS/USBL的标定方案，克服了水下复杂环境下导致标定精度下降的缺陷[7]。

为了对标定算法进行深入探索，本文针对姿态矩阵小角度近似时产生误差的问题，提出了一种基于迭代扩展卡尔曼滤波（Iterative Extended Kalman Filter,IEKF）的安装偏差标定算法，推导了非线性量测模型，并进行了车载试验验证，试验结果表明了所提算法的有效性。

1 超短基线系统定位原理

超短基线系统由水听器和应答器构成，通过声波信号往返于水听器和应答器间的传输时间和声波速度获得载体和水下应答器间的斜距信息，并且根据各个水听器接收声波信号的相位差确定载体的姿态。超短基线系统具有体积小、精度高的优点，被广泛应用在水下潜航器中[8]，图1为超短基线系统的定位原理图。两条基线上安装有四个水听器，同一条基线上的两个水听器间的距离为d，水下应答器的位置坐标为T(xu,yu,zu)。

由超短基线系统定位原理图和几何原理可得[9]：

其中，r为超短基线基座到水下应答器之间直线的距离，m为距离r在水平面oxy上的投影，r与x轴和y轴的夹角分别为xθ和yθ，m与x轴的夹角为θ。

设x轴两个水听器接收声波的相位差为xφ，y轴两个水听器接收声波的相位差为yφ，λ为声波的波长，则有：

由几何关系可得：

由式(1)-(3)可得：

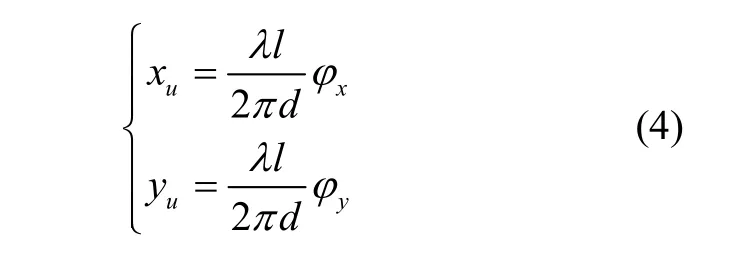
其中，超短基线基座到水下应答器之间直线的距离r可由声波大小和往返时间确定，相位差xφ和yφ由超短基线量测系统内部测量及计算得到。

2 SINS/USBL系统安装偏差角标定算法

2.1 坐标系定义

（1）地球坐标系（e系）：坐标原点取在地球中心，oxe轴在赤道平面与载体当地子午面的交界线上，oze沿极轴方向，oxe轴、oye轴和oze轴构成右手坐标系[10]。

（2）选取“东-北-天”坐标系为导航坐标系（n系）。

（3）定义“右-前-上”坐标系为载体坐标系（b系）。

（4）超短基线基座坐标系（u系）：定义取短基线基座的中心为原点，xu轴、yu轴、zu轴分别指向载体的右前上，由于安装偏差的存在，u系与载体坐标系b系不重合。

2.2 安装偏差角定义

载体坐标系（b系）和超短基线基座坐标系（u系）之间的转换可以用三次旋转得到的姿态旋转矩阵表示[11]。

图2所示为坐标系变换图，载体坐标系首先绕zb轴逆时针旋转ψ角，再绕xb

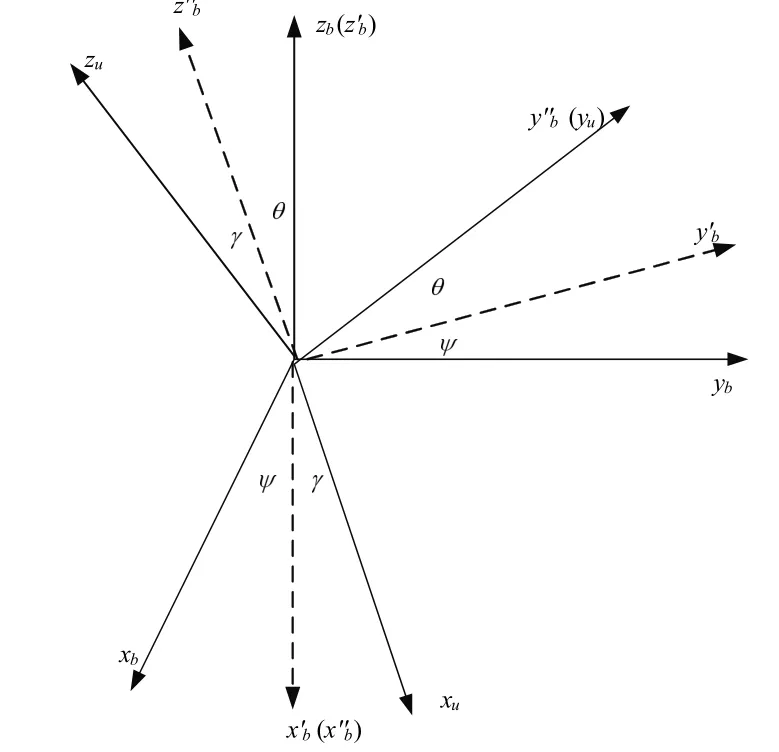
图2 坐标系变换图Fig.2 Coordinate system transformation diagram

'轴逆时针旋转θ角，最后绕轴逆时针旋转γ角得到超短基线基座坐标系。通过三次坐标轴旋转得到从b系到u系的姿态旋转矩阵，表示为：

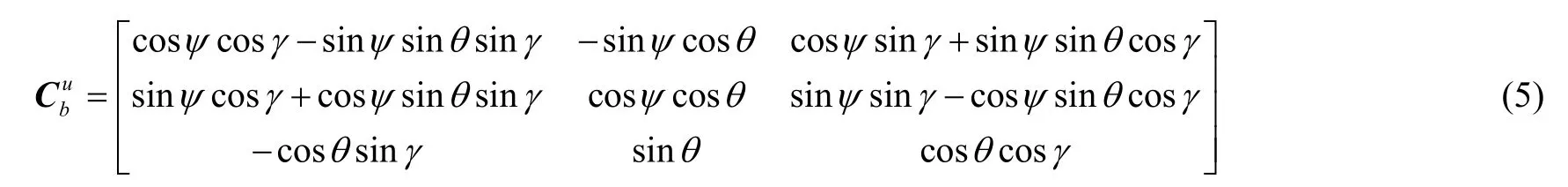
其中，θ为俯仰安装偏差角，γ为横滚安装偏差角，ψ为航向安装偏差角。

2.3 IEKF标定算法模型

迭代扩展卡尔曼滤波（Iterative Extended Kalman Filter,IEKF）是在扩展卡尔曼滤波（Extended Kalman Filter,EKF）上发展而来的，适用于对非线性系统进行滤波估计，并且IEKF对状态估计值进行了多次迭代，滤波的精度更高[12]。

对于状态方程为线性，量测方程为非线性离散系统的状态空间模型，如式(6)所示[13]：

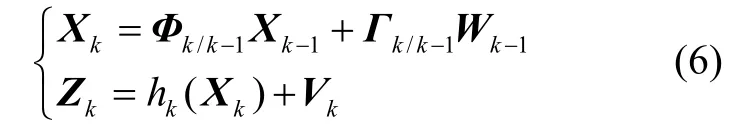
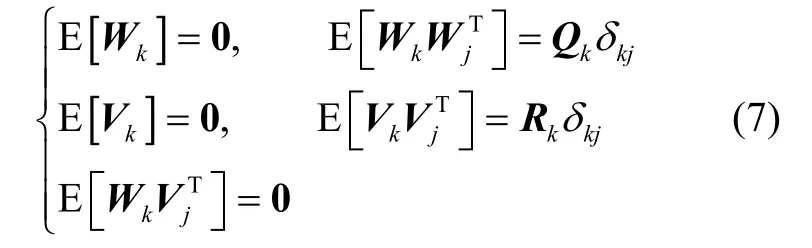
IEKF滤波器的时间更新公式如式(8)所示：

IEKF滤波器的量测更新公式如式(9)所示：

3 车载半实物试验与分析

3.1 半实物仿真条件

图3为车载试验组合导航设备图，车载轨迹如图4所示，绕着建筑楼宇进行1500 s的车载试验，全程进行SINS/GPS组合导航，起始位置纬度为45.7703 °，经度为126.6816 °，车载试验高度视为0 m，终点位置纬度为45.7693 °，经度为126.6828 °。USBL系统输出的数据均由仿真生成，水下应答器的位置坐标设定为（45.7703 °，126.6816 °，-500 m），超短基线系统输出的位置坐标矢量由PHINS/GPS组合导航输出位置坐标与水下应答器的位置坐标分别投影到u系并相减构成。

图3 车载半实物仿真试验设备图Fig.3 Equipment diagram of on-board hardware in the loop simulation experiment

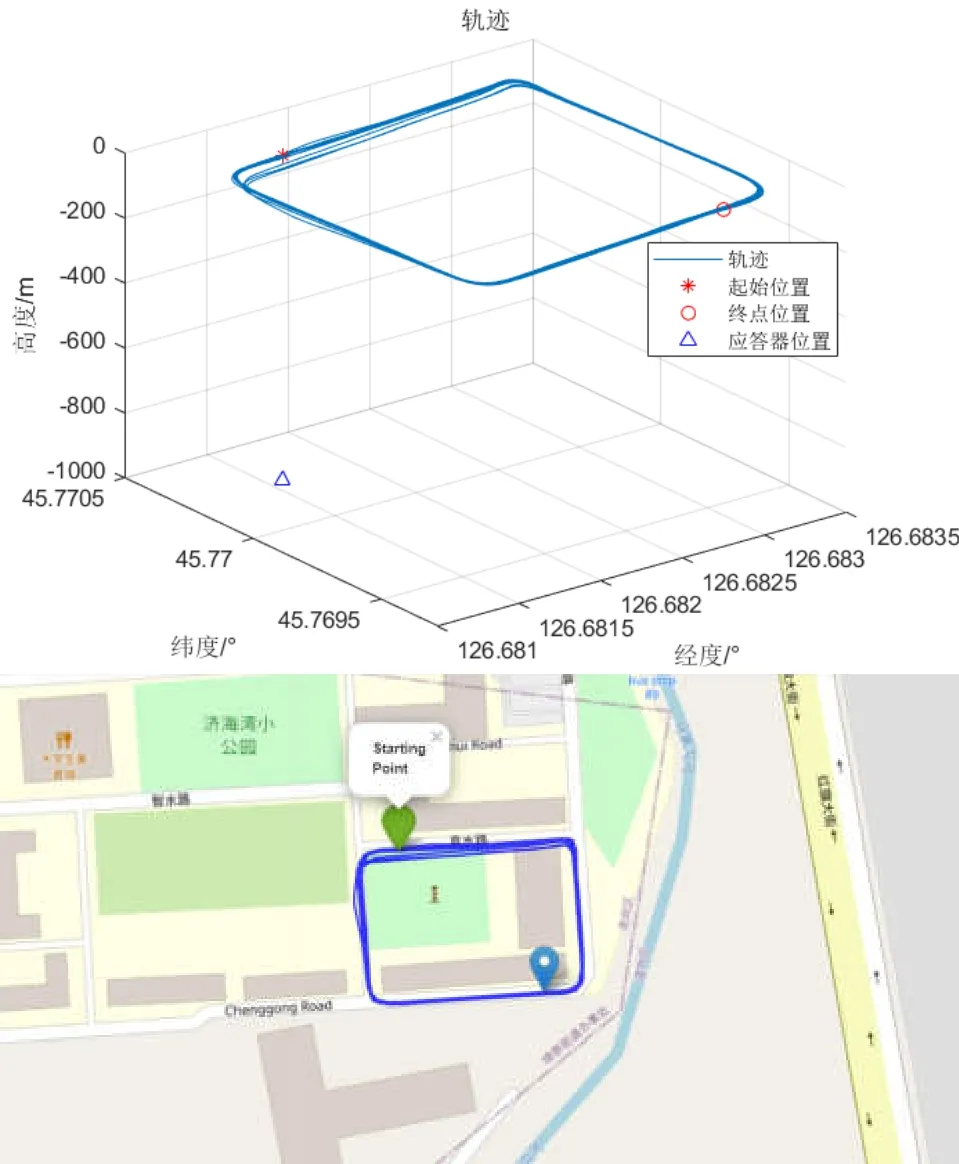
图4 车载半实物仿真试验轨迹图Fig.4 Trajectory diagram of on-board hardware in the loop simulation experiment

3.2 单次仿真试验

进行单次离线仿真试验，设置安装偏差角θ、γ、ψ分别为5 °、5 °、40 °。为了验证基于IEKF标定算法的有效性和优越性，同时进行了基于小角度近似原理的递推最小二乘（Recursive Least Squares,RLS）标定算法和扩展卡尔曼滤波（EKF）标定算法，设置IEKF的最大迭代次数为10次，设置阈值为10-10rad，当前后两次状态估计值之差的模长小于阈值或者达到最大迭代次数就结束当次迭代。三种算法的安装偏差角标定结果如图5-7所示。

图5为基于小角度近似原理的RLS标定算法，θ、γ、ψ标定结果分别为5.4479 °、1.8140 °、37.0705 °。图6为基于EKF的标定算法，θ、γ、ψ标定结果分别为4.8021 °、4.9113 °、39.7024 °。图7为基于本文所提的IEKF标定算法，θ、γ、ψ标定结果分别为4.8961 °、4.9635 °、39.8601 °。从标定结果可以看出基于IEKF的标定算法精度高于其他两种标定方法，由于RLS标定算法对矩阵进行了小角度近似，故其标定精度最低，标定结果统计数据如表1所示。

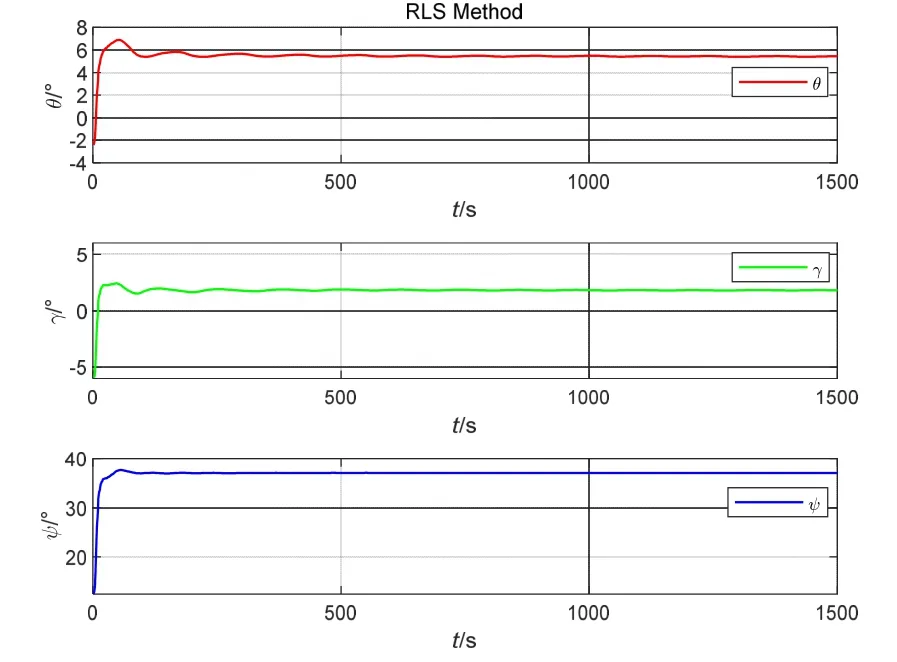
图5 RLS方法标定结果Fig.5 RLS method calibration result

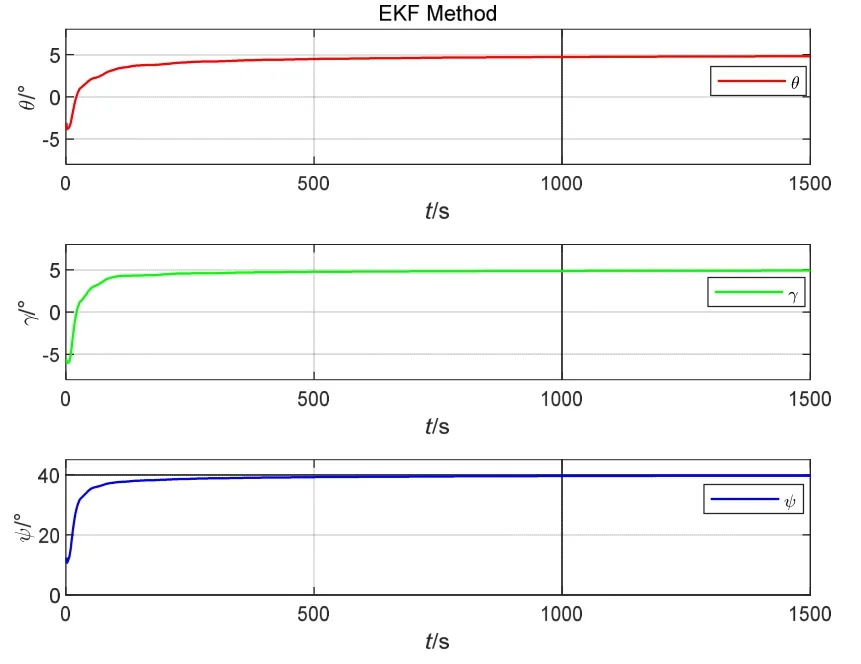
图6 EKF方法标定结果Fig.6 EKF method calibration result

图7 IEKF方法标定结果Fig.7 IEKF method calibration result

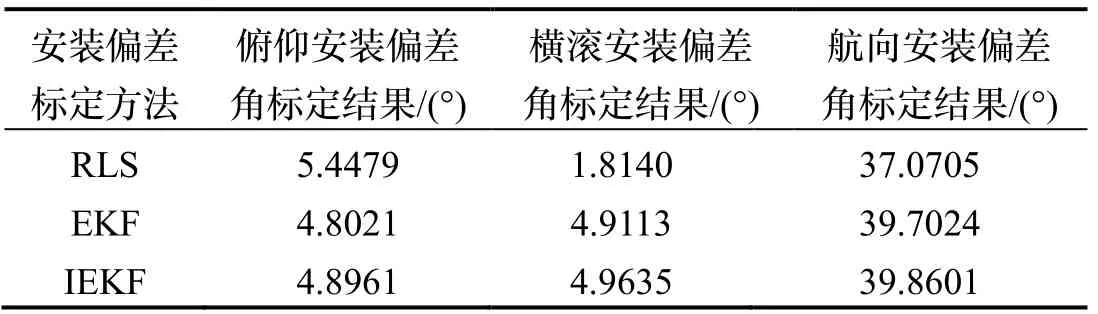
表1 三种算法标定结果Tab.1 Calibration results of three algorithms

三种标定算法对安装偏差角的标定误差曲线如图8-10所示，从标定误差曲线可以看出，IEKF标定算法精度高于EKF算法和RLS算法。

图8 三种算法的俯仰安装偏差角标定误差曲线Fig.8 Calibration error curve of pitch installation deviation angle based on three algorithms

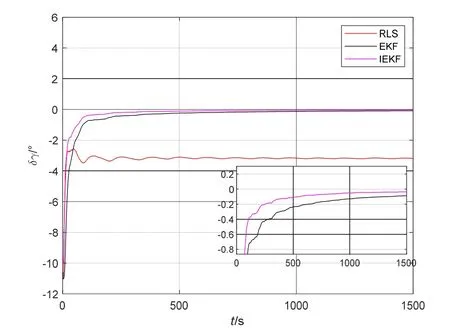
图9 三种算法的横滚安装偏差角标定误差曲线Fig.9 Calibration error curve of roll installation deviation angle based on three algorithms

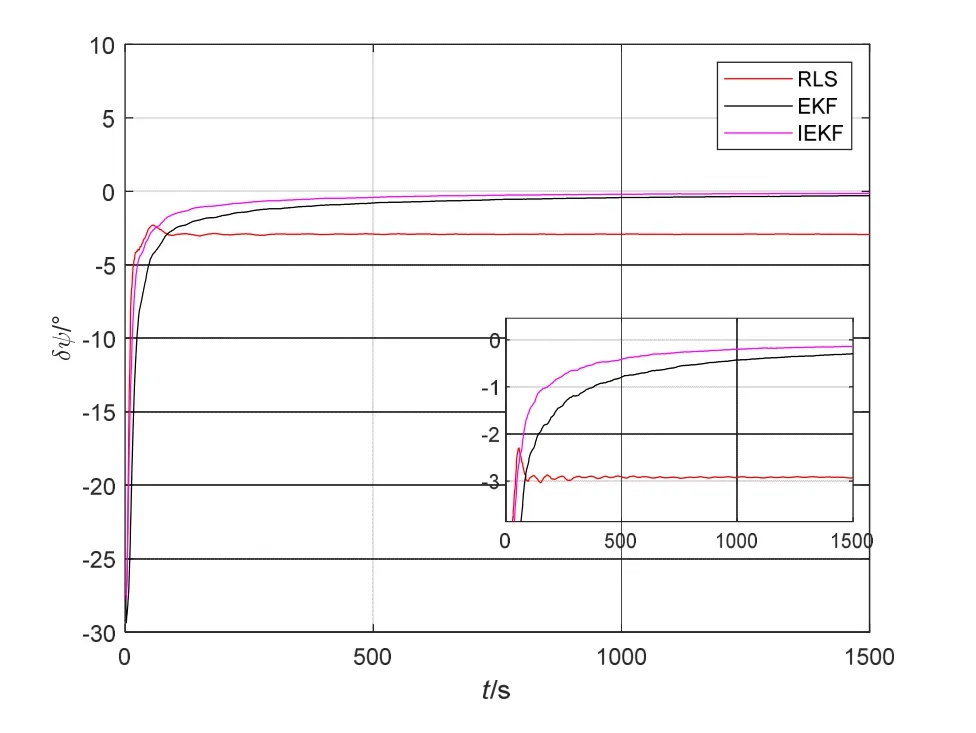
图10 三种算法的航向安装偏差角标定误差曲线Fig.10 Calibration error curve of heading installation deviation angle based on three algorithms

标定误差结果统计数据如表2所示，IEKF标定算法相比RLS算法和EKF算法俯仰安装偏差角标定精度分别提高7.56%和1.96%；横滚安装偏差角标定精度分别提高173.62%和1.06%；航向安装偏差角标定精度分别提高7.52%和0.39%。

表2 三种算法标定结果误差Tab.2 Error of calibration results of three algorithms

3.3 蒙特卡罗仿真试验

为了进一步证明所提标定算法的有效性和优越性，利用车载组合导航数据进行50次蒙特卡罗半实物仿真试验，每次仿真设置的安装偏差角在单次仿真试验设置的基础上加上方差大小为3 °的随机值，50次蒙特卡罗仿真误差结果如图11-14所示。

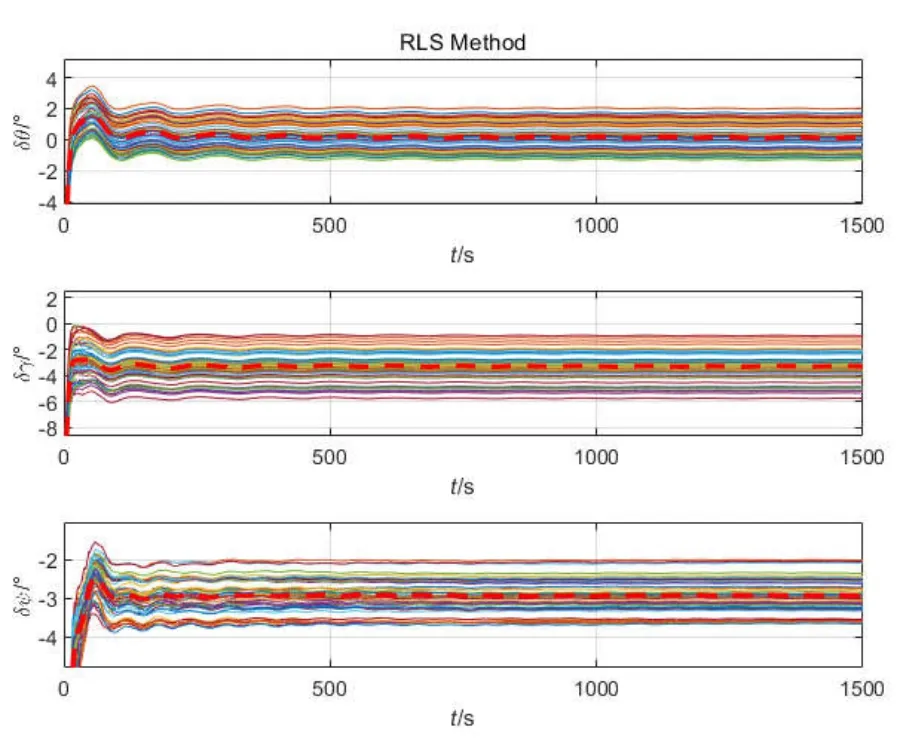
图11 RLS方法标定误差曲线Fig.11 RLS method calibration error curve

图12 EKF方法标定误差曲线Fig.12 EKF method calibration error curve

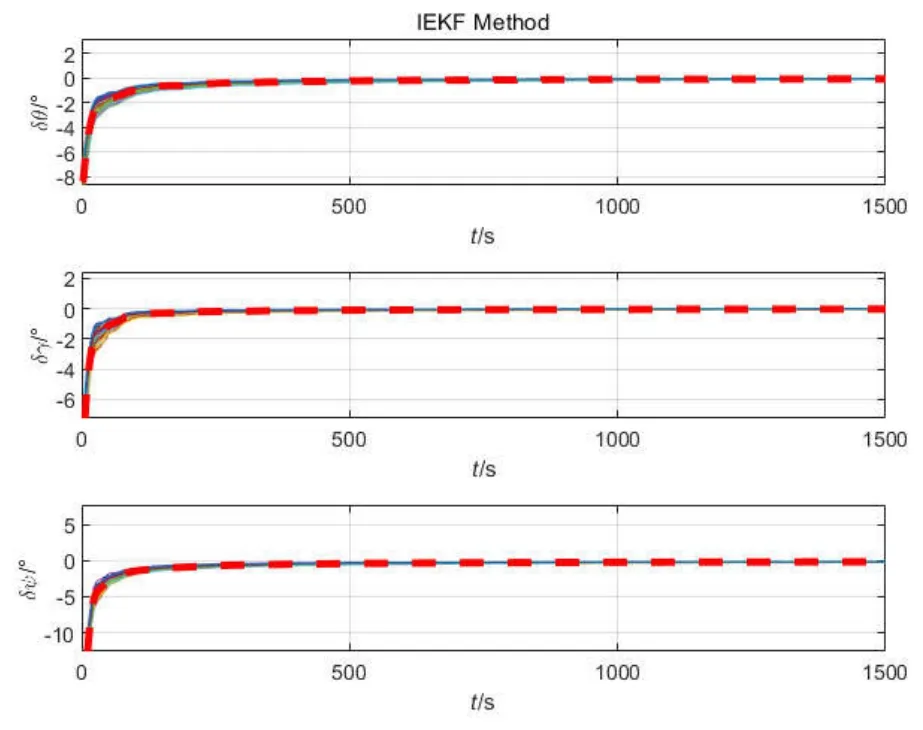
图13 IEKF方法标定误差曲线Fig.13 IEKF method calibration error curve

图11-13为三种标定算法的50次蒙特卡罗标定误差曲线，其中红色的粗虚线为50次标定的误差均值，误差均值统计参数如表3所示，误差标准差统计值如表4所示。图14为三种算法的安装偏差角标定误差均值曲线，可以看出IEKF标定算法可以对三个安装偏差角进行有效标定，并且对于三个安装偏差角的标定误差和标定误差标准差均小于其他两种方法，IEKF标定算法相比RLS算法和EKF算法俯仰安装偏差角标定精度分别提高16.44%和2.60%；横滚安装偏差角标定精度分别提高157.69%和1.17%；航向安装偏差角标定精度分别提高7.50%和0.41%，从标定精度看IEKF标定算法对大安装偏差角也具有较好的估计效果。

图14 三种算法标定误差均值曲线Fig.14 Calibration error mean curve of three algorithms

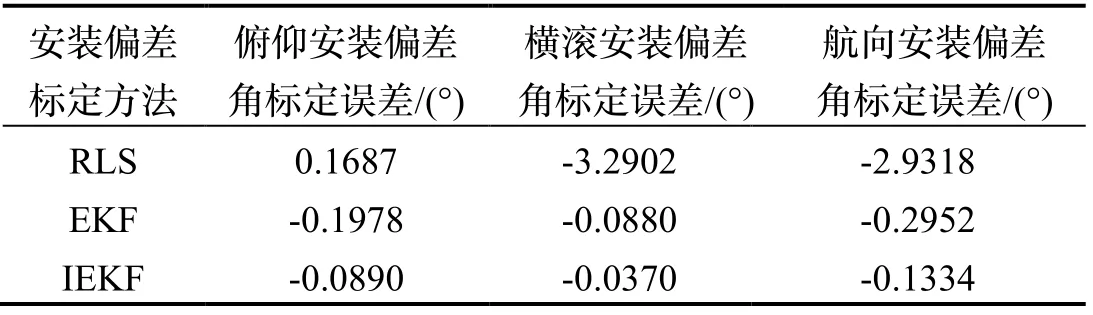
表3 三种算法标定结果误差均值Tab.3 Error mean of calibration results of three algorithms

表4 三种算法标定结果误差标准差Tab.4 Standard deviation of calibration results of three algorithms

4 结论

SINS/USBL组合导航系统的安装偏差角的标定结果对于水下潜航器的导航定位至关重要，为了更加准确地得到标定结果，本文所提方法首先根据安装偏差角的定义和超短基线定位原理建立非线性量测模型，然后基于IEKF滤波算法对安装偏差角进行滤波估计，最后进行了车载试验，并与其他两种标定算法进行对比，对比试验结果表明：基于IEKF的标定算法可以有效地对SINS/USBL组合系统的安装偏差进行估计，并且具有较高的标定精度和稳定性。