基于改进遗传算法的多波束水下地形匹配方法

张 涛，张 驰，张佳宇

（1.微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2.东南大学 仪器科学与工程学院，南京 210096）

惯性导航系统（Inertial Navigation System,INS）是目前自主水下航行器（Autonomous Underwater Vehicle,AUV）最常用的导航方式，但是由于系统本身特性的原因，导航误差会随时间逐渐累积[1]，无法满足AUV长航时的作业需求。为解决这一问题，可以利用地形匹配的结果对INS进行校正。地形匹配是一种利用地球物理信息进行位置定位的方法，将实时测量得到的水深数据与预先存储的水下地形图进行匹配，进而确定AUV在地形图上的位置[2,3]。由于短时间内水下地形不会发生变化，且无需接受其他外部传感器信号，地形匹配具有很高的可靠性和隐蔽性[4]。

目前，地形轮廓匹配算法（Terrain Contour Matching,TERCOM）和最近等值线迭代算法（Iterative closest contour point,ICCP）是最常用的两种水下地形匹配方法[5]。TERCOM通过计算测量地形序列和背景地形的相关性对航迹进行修正，实现简单，但是该算法精度较低，对航向误差要求较高，一般要小于2 °，否则会匹配失败。ICCP在测深序列等值线附近对航迹进行多次迭代变换，逐步靠近真实位置，在初始定位误差较大时，匹配耗时长，定位精度低甚至失败[6]。文献[7]在TERCOM算法的基础上，引入不规则三角网模型替代传统网格化水下地形图，能够有效降低误匹配的概率，同时定位精度高于传统的TERCOM算法。文献[8]利用最小二乘对ICCP匹配结果进行仿射修正，改善ICCP仅能做刚性变换的缺陷，提高匹配定位效果。文献[9]提出一种联合TERCOM和ICCP的匹配算法，利用TERCOM进行粗匹配，ICCP进行精匹配，克服ICCP在初始定位差较大时容易匹配失败的问题。文献[10]对ICCP的采样方式进行改进，结合滑动窗搜索的方式缩小搜索范围，提高了ICCP算法的实时性。以上方法都是基于单点测深系统进行匹配，获取的地形信息有限，在地形相似区域匹配精度较低。随着海洋探测技术的发展，多波束测深系统在在水下地形探测方面发挥着重要作用，不同于传统单波束测深方式，多波束测深系统一次测量能够获得多点地形数据，探测范围更广，精度更高。

本文提出基于改进遗传算法的多波束水下地形匹配方法，在多波束测深系统采集的水深数据中选择多条水深数据，利用遗传算法进行地形匹配，引入正余弦算法对遗传算法中的精英个体进行优化，加快遗传算法的收敛速度和改善局部收敛问题，可以有效改善地形匹配算法在初始位置误差较大时，匹配定位误差大、成功率低的问题。

1 水下地形匹配模型

水下地形匹配的基本思想是根据AUV实时测量的地形信息与提前存储的水下地形图进行比对，对INS指示的航迹进行变换，从而确定AUV当前位置。在进入地形匹配适配区之前，由于惯性元件累积误差的影响，INS指示的航迹与真实航迹之间存在初始平移位置误差，航向误差和速度误差。实际中完成一次地形匹配所需时间较短，可认为在匹配期间航向误差和速度误差为定值，因此惯导解算的速度v和航向h可以表示为：

2 基于正余弦算法的改进遗传算法

2.1 遗传算法

遗传算法（Ggenetic Algorithm,GA）是一种借鉴自然界生物进化过程而构造出的优化搜索算法，根据“优胜劣汰”原则，迭代更新种群，使得种群向着最优的方向进化[11]。遗传算法从初始种群出发，根据建立的适应度函数对种群中个体的优劣进行评价，通过选择、交叉、变异等遗传操作对种群中个体进行变换以产生整体性能更优的新种群，多次迭代后找到全局最优解。为保证算法的收敛性，一般在种群更新过程中加入精英策略，对于每代个体中的最优个体，不进行更改，直接保留到下一代种群中，让每代种群的最优个体能够顺利进入后续的迭代计算中。

以INS指示位置为搜索中心，在搜索空间内生成多组仿射变换参数(tx,ty,α,θ)，对INS指示航迹进行变换，利用遗传算法对变换参数进行迭代计算，最后得到最优变换参数，对应航迹即为最接近真实位置的匹配航迹。

2.2 正余弦算法

正余弦算法（Sine Cosine Algorithm,SCA）是一种基于正弦和余弦数学模型的优化算法，利用正弦余弦函数震荡性特点来趋近最优解[12]。其算法过程与传统的基于种群的优化算法类似，根据建立的适应度函数，对初始生成的候选解进行多次循环迭代，最终得到最优个体。正余弦优化算法计算简单，方便实现，调节参数少，收敛速度快，因此非常适用于参数的快速寻优。

SCA在待搜索区间内随机初始化生成候选解种群，设种群规模为N，包括N个个体(X1,X2...XN)，根据适应度函数计算适应度值fSCA(Xi)，记录最优个体位置，通过正余弦函数与随机因子对候选解更新，生成下代种群，具体更新方程为：

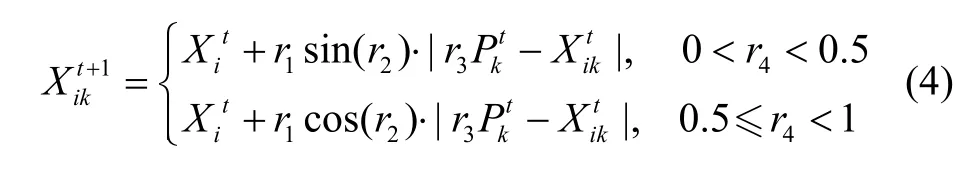
式中，k为待优化参数的第k维，t为当前迭代次数，Xt+1为下一代个体，Xt当代个体，Pt为当代最优个体：三个参数是随机因子，均服从均匀分布，r1为转换参数，控制SCA从全局开发转向局部开发，取值为：

其中，a为常数，T为设定的最大迭代次数。

2.3 基于SCA改进的遗传算法

GA为保证算法的收敛性，通常加入精英策略，但是在精英个体是局部最优的情况下，精英策略则加剧局部最优个体对整体种群的影响，种群中其他个体向局部最优靠拢，导致算法快速收敛于局部最优。针对这个问题，引入SCA对每代种群的精英个体进行优化。

设GA搜索区域大小为(εx,εy,εα,εθ)，分别对应横向平移、纵向平移、缩放量和旋转角的最大变化量。SCA以每一代种群中的精英个体为搜索中心，设定搜索区间大小为(0.1εx,0.1εy,0.2εα,0.2εθ)，在此区间内生成候选集，利用更新方程对其进行候选解更新，得到最优解。SCA的最优解替换GA原来的精英个体，并将SCA的候选解种群作为外部种群，与遗传算法的种群合并，一起进行后面的遗传操作，使得种群向最优方向进行进化。

3 基于改进GA的多波束地形匹配方法

3.1 多波束水深数据选择

传统利用单波束系统进行地形匹配的方法，每次测量只能获得单点水深信息，进行多次测量之后，得到多个位置点的水深信息与INS数据，组成单条水深序列，利用水深序列与水下地形图进行比对，确定载体在地图上的位置。当INS指示航迹与真实航迹初始定位误差较大时，由于需要搜索的范围扩大，非常容易出现地形相似的地方，利用单条水深序列进行地形匹配的方法精度会大大下降甚至发生误匹配。

不同于单波束系统，多波束测深系统一次测量能够得到一条与航向垂直的水深条带，包含几十甚至上百个水下地形深度信息，因此可以选择测量数据中的多个测深数据点同时进行地形匹配，提高算法在初始位置误差较大或相似地形区域的匹配定位精度。考虑算法复杂度，在每次测深数据的中心位置和两侧间隔为dΔ的位置各选择一个水深点，组成三条水深序列。间隔dΔ根据地形标准差进行自适应计算得到：

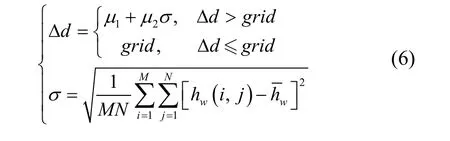
其中，μ1和μ2为调节系数，grid为地形图网格间距，σ为M×N个网格的地形标准差，hw(i,j)为位置(i,j)处的测量水深，为该地区的平均水深。

3.2 适应度计算

适应度函数用于反映匹配航迹和真实航迹之间的相似度，相似度越大，意味着匹配航迹越靠近真实航迹。GA中的适应度函数由三条多波束测量水深与匹配航迹在水下地形图上插值得到水深的差值的加权和构成，根据多波束测深系统的测深特性，中间区域的测量数据误差最小，越靠近两侧边缘测量数据误差越大，所以给三条水深序列分配不同的权重：

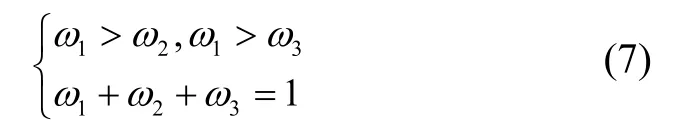
式中，1ω为中间序列权重，2ω和3ω分别为左右两侧序列权重，均为常值。

考虑到匹配过程中，INS的累计误差逐渐增加，导致航迹后期的位置可信度逐渐降低，因此加入衰减系数λ，逐渐减小水深序列中数据点所占权重，适应度函数具体形式为：

式中，i对应三条水深序列，j对应每条序列上的匹配点，ijc为匹配航迹在水下地形图上映射的水深，*ijc为实际测量水深，N为测量序列点数。匹配航迹水深与实际测量水深的差值越小，适应度函数值越大，适应度函数值取得最大值时，此时匹配航迹最接近真实航迹。

与GA不同，SCA的适应度函数值越小，表示待优化参数越接近最佳值。在进行SCA优化时，种群中的个体均在精英个体附近，较为接近真实航迹位置，此时对最大水深误差更加敏感，SCA的适应度函数为：

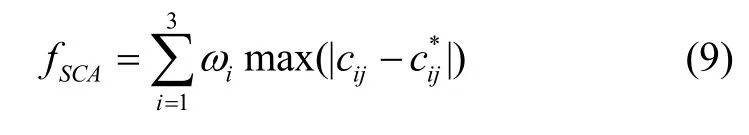
3.3 基于SCA改进GA的多波束地形匹配步骤

根据上述分析，基于SCA改进GA的多波束水下地形匹配方法的具体步骤如下：

步骤一：在多波束测深系统的测深数据中选取三条水深序列，分别赋予不同权重。

步骤二：以INS指示航迹位置为搜索中心，设定搜索区间，在搜索区间内随机生成GA初始种群。

步骤三：对INS指示的初始航迹进行仿射变换，在水下地形图上进行双线性插值，得到变换后航迹对应的水深，计算变换航迹的适应度函数值。

步骤四：判断迭代是否停止，满足终止条件则输出结果，否则，使用精英策略，保留精英个体。

步骤五：利用SCA对精英个体进行优化，生成外部种群与GA种群合并进行遗传操作。

步骤六：更新种群，跳转至步骤三。

图2 改进GA的多波束地形匹配流程图Fig.2 Flow chart of multi-beam terrain matching based on improved GA

4 仿真验证

为验证本文所提方法的有效性，对基于改进遗传算法的多波束地形匹配方法进行仿真实验。实验基于我国某地区实际测量的水下地形数据，地形图的网格数为1484 1157×，网格间距为1 m，选择其中两块不同地形特征区域设置仿真航迹，图3和图4为航迹对应的水下投影点和地形图，两处地形的特征参数如表1所示。

图4 航迹B及对应地形图Fig.4 Track B and corresponding topographic map

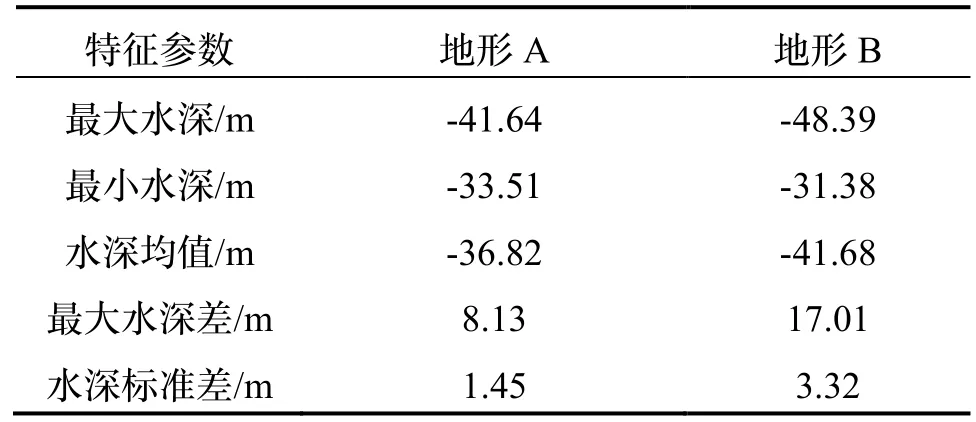
表1 地形特征参数Tab.1 Terrain feature parameters

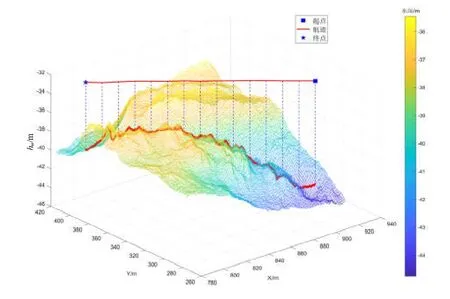
图3 航迹A及对应地形图Fig.3 Track A and corresponding topographic map

仿真中AUV移动速度为3 m/s，每隔4 s进行一次采样，15个采样点组成一个匹配序列，测量水深为真实水深增加标准差为0.3 m的白噪声。航迹A的起始位置为(942,405)m，航向为北偏西60°；航迹B的起始位置为(775,245)m，航向为正东方向。惯性元件参数如表2所示。

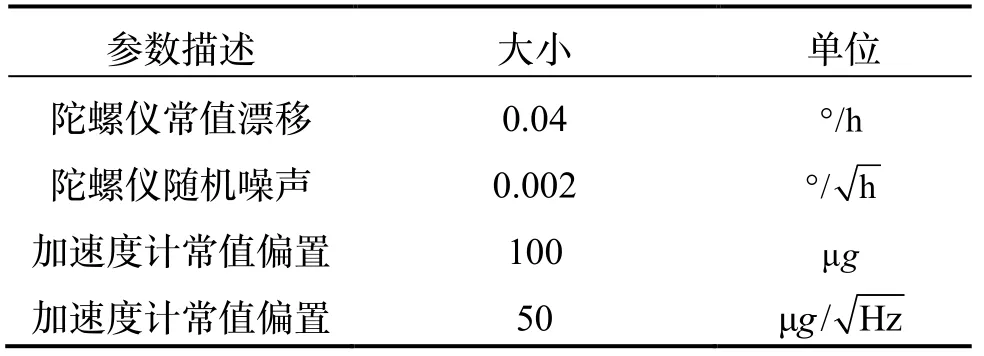
表2 惯性器件误差Tab.2 Inertial device error

根据上述仿真条件，仿真验证文献[13]提出的多路径并行ICCP算法和本文提出的基于改进遗传算法的多波束地形匹配方法，分别对航迹A和航迹B设置两种不同大小的初始误差，进行匹配定位，其匹配结果如图5-8所示。

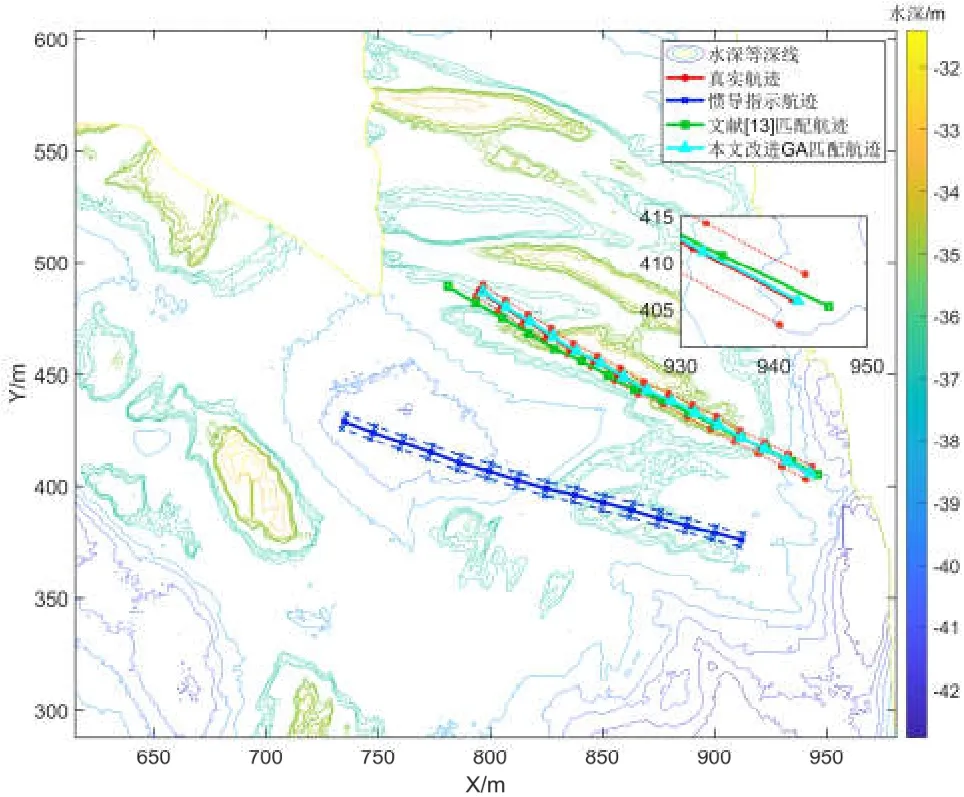
图5 航迹A初始误差较小时匹配结果Fig.5 Matching results of small initial error of track A

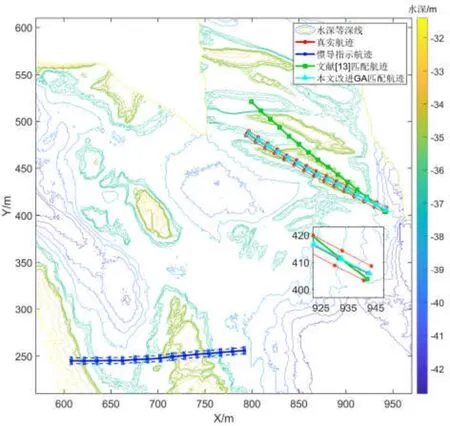
图6 航迹A初始误差较大时匹配结果Fig.6 Matching results of large initial error of track A

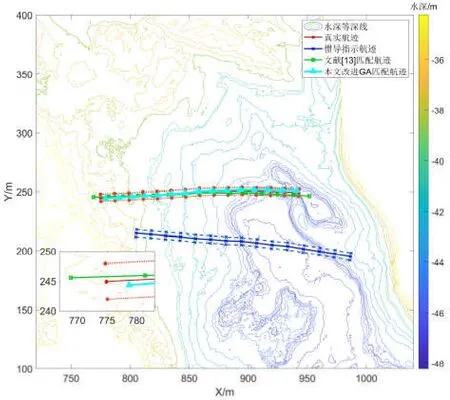
图7 航迹B初始误差较小时匹配结果Fig.7 Matching results of small initial error of track B

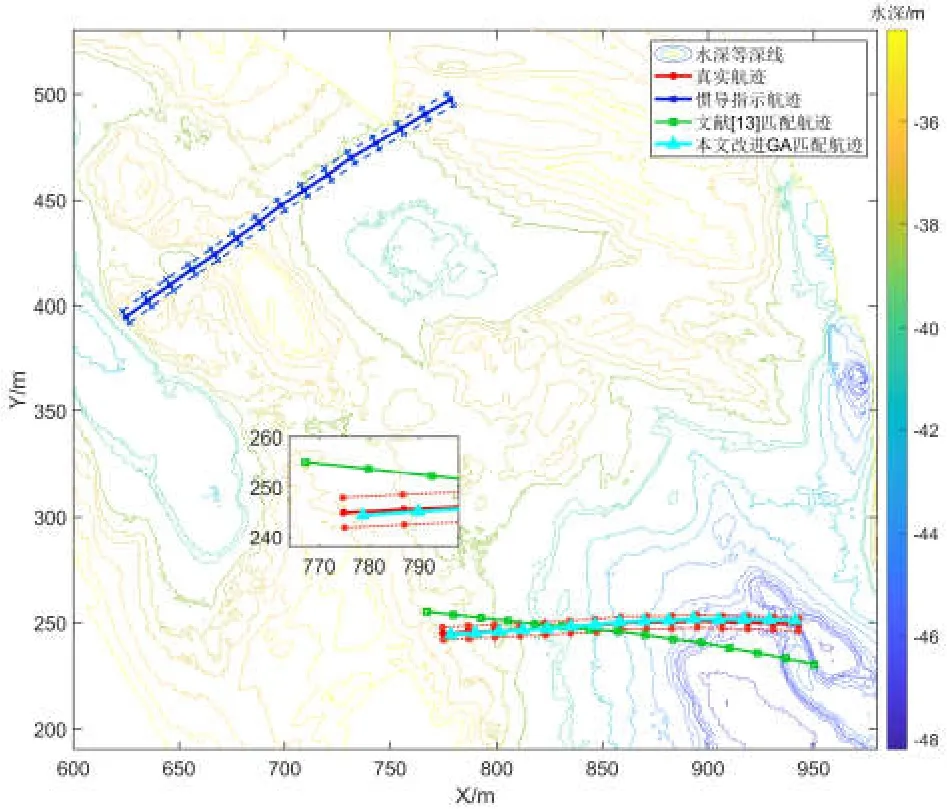
图8 航迹B初始误差较大时匹配结果Fig.8 Matching results of large initial error of track B

图中红色实线为真实航迹位置，同时对应于中间水深序列，红色虚线为实测多波束水深数据中选取的两侧水深点对应的位置；蓝色实线代表惯导指示航迹，对应于中间水深序列的指示位置，两侧的虚线为另外两条水深序列指示位置；绿色实线和天蓝色实线分别为多路径并行ICCP匹配航迹和本文方法匹配航迹。从仿真结果图可知，在初始误差较小时，多路径并行ICCP与本文所提方法均能成功匹配，匹配航迹均在真实航迹附近；在初始位置误差较大时，由于惯性累积误差的影响，导致航迹变形严重，并且搜索范围增大，多路径并行ICCP匹配效果较差，匹配航迹与真实航迹之间误差较大，而本文所提方法匹配结果仍然在真实航迹附近，对初始误差的大小不敏感。

仿真结果数据如表3所示，从表中可以看出，多路径并行ICCP在初始位置误差较大时，匹配航迹的平均误差在10 m左右，而本文所提方法在不同初始位置误差的条件下，匹配航迹的平均误差在2 m左右，航迹上的最大匹配误差小于4 m，定位精度大大优于多路径并行ICCP算法，能够更好实现不同初始位置误差条件下的地形匹配。

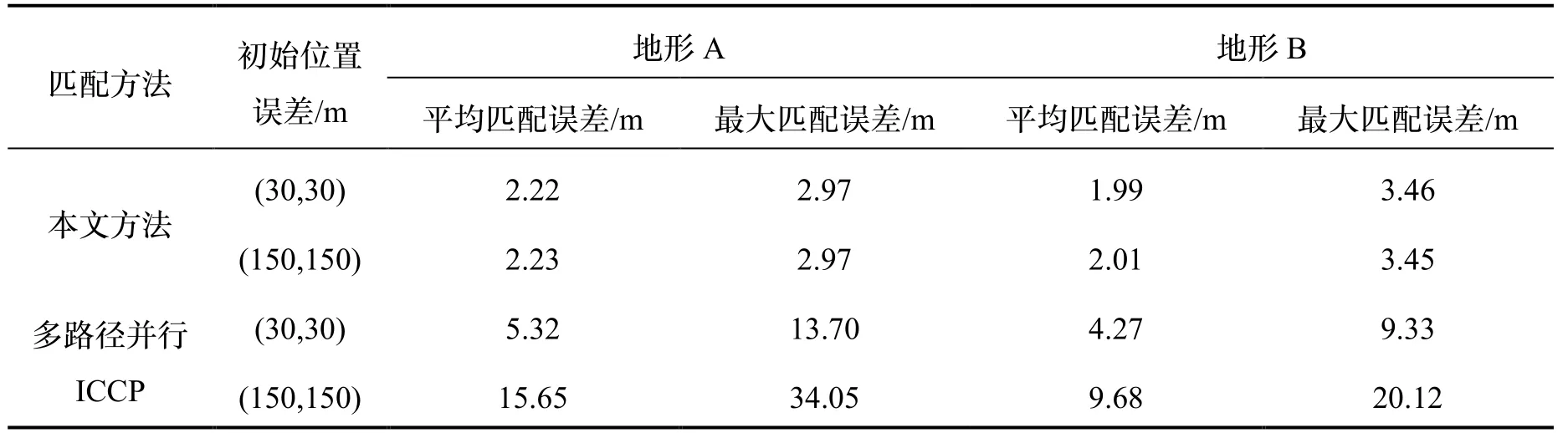
表3 匹配结果对比Tab.3 Comparison of matching results

为进一步验证改进遗传算法的效果，在航迹A(150,150)m初始位置误差的条件下进行航迹A四组匹配定位实验：实验A使用本文所提算法进行地形匹配；实验B在传统遗传算法的基础上，使用本文提出的适应度函数；实验C在传统遗传算法上加入SCA进行优化；实验D使用传统遗传算法进行匹配，使用三条水深序列的水深差值直接累加和作为适应度函数。每组实验独立进行50次，分别计算每组实验的平均定位误差、算法最终收敛时的平均迭代次数和平均运行时间，实验结果如表4所示。

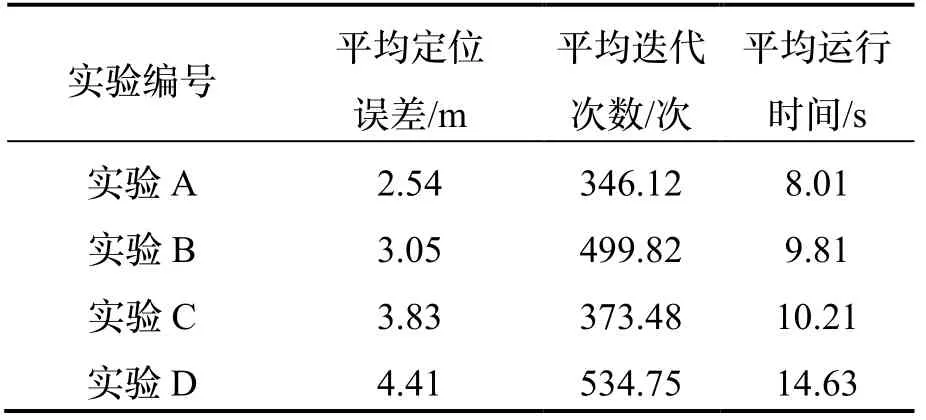
表4 遗传算法对比实验Tab.4 Comparative experiments of GA

对比实验A和实验D结果可知，本文所提算法匹配结果相比于传统遗传算法定位精度提高42.4%，平均迭代次数降低35.27%，平均运行时间减少45.25%。对比实验B和实验D可知，使用本文提出的适应度函数，遗传算法的定位精度得到显著提高，表明本文提出的适应度函数能够更好地衡量匹配航迹与真实航迹之间的相似度，有利于提高算法定位精度。对比实验C和实验D可知，加入SCA优化后，遗传算法收敛时的迭代次数和运行时间明显降低，算法的运行效率得到提高。通过以上四组重复性实验的统计结果可以得出，在遗传算法中加入SCA优化和改进适应度函数能够有效提高遗传算法的匹配定位精度，加快收敛速度，遗传算法的改进效果得到验证。

5 船载验证

为进一步验证本文所提方法在实际应用中的效果，在千岛湖某水库区域进行实际船载实验。图9为本次实验的实验船，船上搭载的主要设备有IMU、多波束测深系统和GPS-RTK接收机。其中，IMU输出频率为200 Hz，其中陀螺仪零偏小于0.02/h°，随机游走小于，加速度计零偏小于100μg，随机游走小于，实验区域地形图的网格分辨率为1 m，多波束测深系统为中海达公司的iBeam 8140，具体参数如表5所示。

图9 试验船及相关试验设备Fig.9 Experimental ship and related equipments

表5 多波束声呐主要技术参数Tab.5 Main technical parameters of multibeam sonar

本次实验选取三条航迹，分别设置不同大小INS初始位置误差，分别为(50,50)m、(150,150)m和(200,200)m。试验中船速约为1.5 m/s，每间隔8秒选择一个匹配点，15个匹配点组成一次航迹。为方便表示，隐去试验区域的经纬度，使用直角坐标系表示位置坐标，由IMU和GPS-RTK进行松组合得到的位置作为真实参考航迹。

图10-12分别为三种不同初始误差条件下的匹配结果，表6为匹配结果数据对比，从匹配结果可以看出，本文所提方法在不同初始位置误差下，匹配航迹的平均位置误差在3 m以内，匹配航迹的最大误差小于8 m，定位结果不受初始位置误差的影响。而多路径ICCP算法的精度要低于本文算法，并且在初始误差增大时，匹配误差也逐渐增大，当初始误差达到200 m时，匹配失败。船载试验结果表明本文所提方法在不同大小的初始误差条件下，均能达到较高的定位精度，方法的实际效果得到验证。

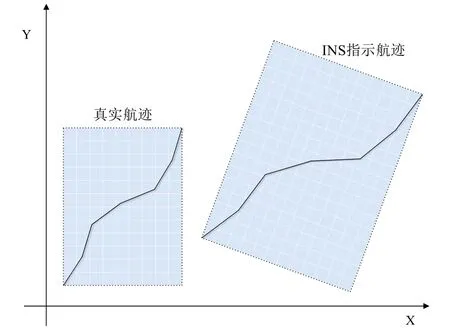
图1 INS指示航迹与真实航迹示意图Fig.1 INS indicated track and real track diagram

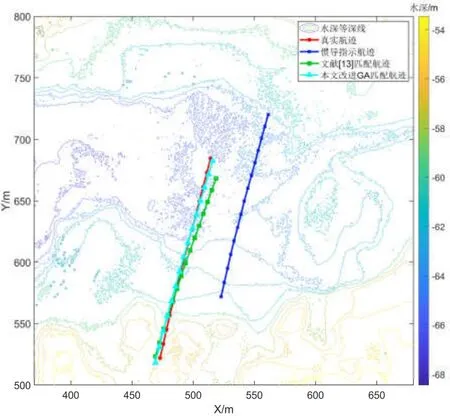
图10 (50,50)m初始位置误差匹配结果Fig.10 Matching results of (50,50)m initial position error

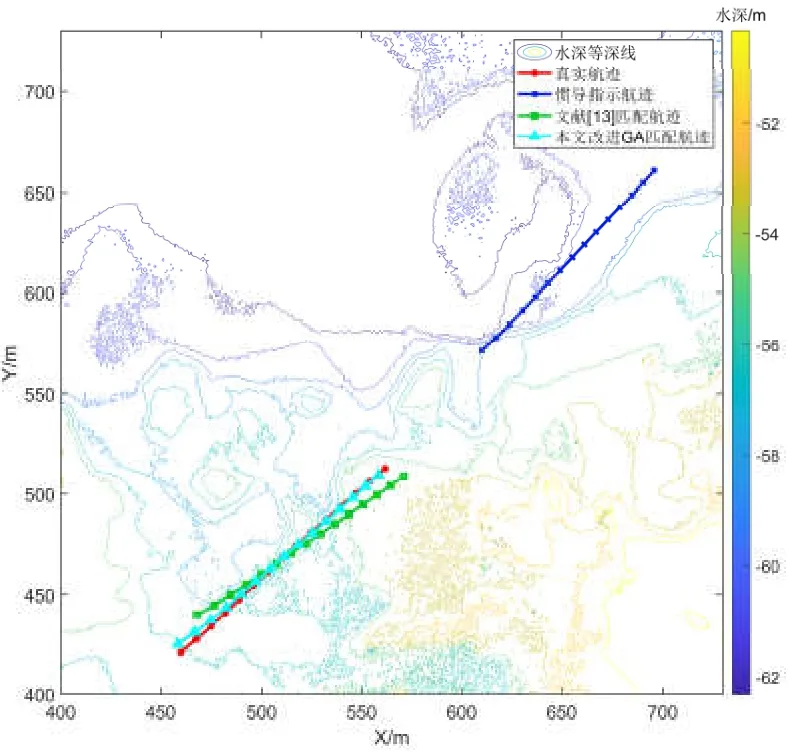
图11 (150,150)m初始位置误差匹配结果Fig.11 Matching results of (150,150)m initial position error

图12 (200,200)m初始位置误差匹配结果Fig.12 Matching results of (200,200)m initial position error

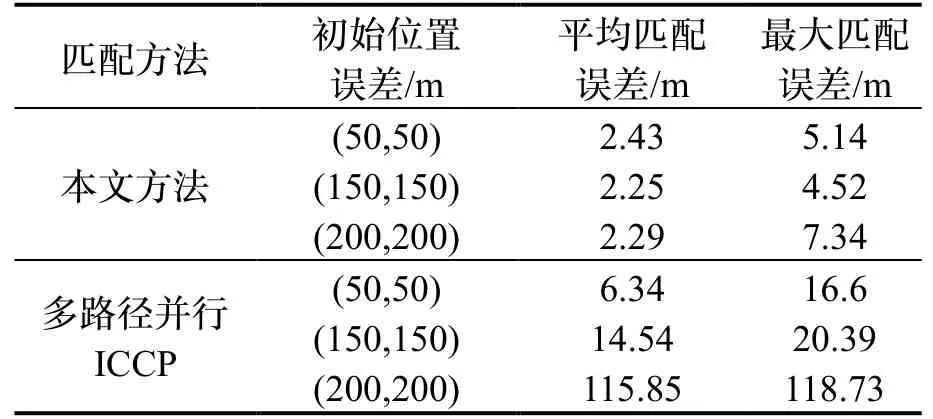
表6 船载实验匹配结果Tab.6 Matching results of shipboard experiments

6 结论

本文针对水下地形匹配问题，提出基于SCA改进遗传算法的多波束地形匹配方法，根据地形特征自适应选择三条水深数据进行匹配，保证算法在相似地形处的定位精度，降低误匹配率；在适应度函数中加入收敛因子，减小后期惯导累积误差的影响；引入SCA对遗传算法进行优化，加快算法收敛速度，降低陷入局部最优的风险。仿真和船载实验结果表明，本文提出的基于改进遗传算法的多波束水下地形匹配方法不受初始误差大小的影响，相比ICCP方法，定位精度更高。