logistic回归在护理研究应用中的注意事项

王奉涛 孟艳雷 张珊 吴越

(1.泰维康医疗器械(上海)有限公司，上海 200050；2.青岛大学附属医院，山东 青岛 266000)

logistic regression即logistic回归分析，又称逻辑回归，是一种广义的线性回归分析模型，实际上属于判别分析，起初用于数据挖掘，经济预测等领域，后被应用于流行病学领域。目前已被引入到护理科研中的横断面调查研究、病例对照研究以及队列研究，在探讨引发疾病或并发症的危险因素、预测疾病的发生风险、临床试验评价、护理措施评价等方面有着广泛的应用[1]。但在实际的护理研究中，有相当一部分研究者在应用logistic回归过程中都或多或少的存在一些误区，这使得部分护理研究的结果与实际情况产生偏差，甚至会得出与实际情况完全相反的结果，降低了研究结果的可信度，也降低了研究质量。本文主要通过实际案例剖析logistic回归应用中的常见问题，旨在为logistic回归在护理研究中的应用提供参考，以期提高护理研究的质量和水平。

1 logistic回归的基本概念及其适用范围

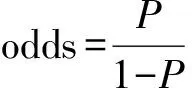
1.2logistic回归的适用范围 logistic回归主要在流行病学中应用较多，现在也已经越来越多的被护理学研究所采用，如寻找疾病或并发症的危险因素；预测在不同的自变量情况下，疾病或并发症发生概率的高低等；在横断面研究和回顾性研究中更为常见。logistic回归的因变量的数据类型必须是分类变量，可以是二分类的，也可以是多分类的，而多分类的logistic回归又分为有序多分类logistic回归和无序多分类logistic回归。而自变量的类型则没有严格的限制，连续变量、等级变量、无序多分类变量都可以作为logistic回归的自变量。

2 logistic回归在应用过程中须注意的问题

图形化的统计软件使得应用logistic回归分析的门槛大大降低，利用统计软件，研究者可以省略大量的运算过程。但另一方面，研究者对logistic回归分析基本原理的理解和应用范围的把握往往不完善。本文将logistic回归在应用过程中须注意的问题归结如下。

2.1样本量问题 logistic回归的统计推断是建立在大样本下的，只有充足的样本量才能保证研究结果的可靠性和稳定性。一项护理研究在确定了研究方法和评价指标之后，可以依据研究类型和评价指标的数据类型进行样本量的计算；但即使满足研究类型和数据类型的要求，样本量也不一定能支持logistic回归分析得出足够可信的结果。样本量不足对logistic回归带来的主要风险是complete separation(完全分离)和quasi-complete separation(半完全分离)这2种现象[2]，表现在结果中是无法得到回归系数B，或者是Waldχ2过大[3]。按照EPV(event per variable)法，每个自变量至少需要10～15个阳性(或阴性，根据研究的实际需要)事件患者，而确保样本量满足EPV的需求，能够在很大程度上避免以上两种现象的发生。logistic回归的样本量要求为阳性(或阴性)事件患者达到混杂因素的10～15倍[3]，而并非要求所有研究对象达到混杂因素的10～15倍；并且真正有效样本量将根据二分类结局中两类结果观察数的最小值而定[2]。比如，某团队为调查了老年人高血压发生的危险因素，回顾并统计了某社区64人的高血压发生情况及其可能的影响因素，结果发现有36人患病。本案例阳性数是36，但是实际上二分类结果中，阴性数量28才是较小值，因此在进行logistic回归时，最多可以纳入研究的因素数量并非64/10，也不是36/10，而应该为28/10，即最多纳入2个影响因素。要想纳入更多研究因素，就必须扩大样本量，找到更多的患者，这是保证统计推断结果可靠性的先决条件，也是护理研究中的常见问题。

2.2数据的适用性

2.2.1数据类型

2.2.1.1自变量和因变量设置问题 logistic回归的因变量为分类变量，可以是二分类变量，如死亡/存活，患病/未患病等。也可以是多分类变量[4]，如等级1/等级2/等级3等，在队列研究或随机对照研究这种前瞻性研究中，评价某种措施或因素对疾病的预防或治疗效果时，logistic回归的因变量不应该简单的分为二分类的有效和无效，而应该根据实际情况分为多分类等级资料。例如某研究在验证某新型敷贴对住院患者压力性损伤的预防效果时，对照组患者压力性损伤发生率为5%，干预组患者为4%，经过二分类logistic回归未发现2组压力性损伤预防效果的统计学差异，但干预组发生压力性损伤的患者中1期压疮的比例为70%，2期为27%；而对照组发生压力性损伤的患者中1期压力性损伤的比例为32%，2期为60%，此时将因变量简单归结为压力性损伤发生与不发生是不合适的；虽然新型敷料不能显著降低压力性损伤发生风险，但却可以将压力性损伤分期控制得更低，对压力性损伤也依然具有预防效果，因此本研究应将压力性损伤的发生分期设置为因变量。然后进行多分类logistic回归，才能使研究结果更接近临床实际情况。

logistic回归的自变量可以是分类变量，也可以是数值变量。在很多研究中，作者往往将年龄、工作年限、住院时长、收入及量表得分等数值变量转换为等级变量再引入logistic回归模型，这种做法本身并不能说是一种错误，但这种做法会带来一系列问题。首先是自变量分组对因变量的效应改变量是否均等的问题(后文会有讨论)，其次在结果讨论时也容易出现偏差，并且分组会降低数据的利用效率。例如某研究在分析社区老年人使用日间照料中心的影响因素时，将年龄分为低龄(60～69岁)、中龄(70～79岁)、高龄(≥80岁)3组，然后引入logistic回归后发现存在统计学差异，得出结论为年龄是社区老年人使用日间照料中心的影响因素，但事实上这个结论并不严谨，因为引入logistic回归的自变量为年龄段而非年龄，作者在对年龄进行分段时就已经默认年龄段内不存在对因变量的影响；即年龄60岁～69岁在logistic回归模型中对因变量的贡献是相同的。所以在类似的研究中，不应该轻易把数值变量转化为等级资料进行统计分析；当然如果作者是想研究不同年龄段是否会是社区老年人使用日间照料中心的影响因素，则这种分组是合适的，但下结论时应严谨。

2.2.1.2哑变量设置 当自变量为数值变量时，可在计算过程中带入原值；当自变量为等级资料时可进行适当赋值后引入logistic回归，当自变量为分类变量时，则应设置哑变量，即设立一个参照水平，将m个分类水平的多分类变量转化成(m-1)个哑变量[5]，如表1，3个哑变量的回归系数分别为β1、β2、β3，第一行是相对于第一水平的优势比，第二行是相对于第二水平的优势比，三、四行类似；也可以将每个多分类变量转化成二分类变量，再引入回归模型，比如血型，将4种血型分别设置为4个二分类变量：A型(是=1，否=0)、B型(是=1，否=0)、O型(是=1，否=0)、AB型(是=1，否=0)，然后再引入回归模型。

表1 各水平间的优势比

在实际应用过程中，往往会有研究者将无序分类变量按照等级变量赋值后进行统计分析的情况。例如某研究在分析儿童耳鼻喉术后谵妄发生现状及影响因素时，将手术部位作为自变量进行单因素分析后发现有统计学差异，遂将其赋值引入logistic回归模型，具体赋值为：耳部手术=1；鼻部手术=2；喉部手术=3；支气管/肺内异物取出术=4；其他=5。但实际上手术部位之间的差别不存在等级关系，这样的赋值方式是一定会使回归模型产生偏差的，最终多因素分析结果显示手术部位无统计学差异，但不恰当的赋值使得此研究的结果的可信性大打折扣。正确的做法是将这5种手术部位设置为哑变量，耳部手术(是=1，否=0)、鼻部手术(是=1，否=0)、喉部手术(是=1，否=0)、支气管/肺内异物取出术(是=1，否=0)、其他(是=1，否=0)，然后引入回归模型进行分析。此外，值得一提的是即使数据为等级资料，其赋值时也必须考虑到自变量的等级变化对因变量效应改变量的影响，即自变量每增加一个等级，因变量的效应改变量是否是相等的。例如某研究在调查三甲医院手术室护士工作压力和职业倦怠与离职意愿之间关系时，单因素分析后将职称作为自变量进行赋值：初级=1；中级=2；高级=3，赋值过程看上去并无问题，但实际上中级职称比初级职称的离职意愿增加量，高级职称比中级职称离职意愿的增加量，基本是不会相等的；因此这样的赋值也是不合理的，如果无法确定自变量等级之间的因变量效应改变量，可以将等级资料也作为无序分类变量，设置哑变量后引入回归模型，这样就可以有效规避此问题。

2.2.2自变量筛选 对于多因素logistic回归分析来说，选择合适的自变量是建立回归模型的基础。筛选自变量的方式，最常见的是先进行单因素回归，然后将P值<0.05的自变量引入模型中，再做多因素回归，然后我们可以再根据前后偏回归系数或者OR值的变化，来协助判断是否需要将其纳入到多因素回归中进行调整和控制。虽然单因素分析的合理性尚存争议，但这种分析思路呈现了从控制单一因素到控制多个混杂因素的变化过程；单因素回归分析的结果对于变量的筛选很有意义，而筛选后的变量将直接决定研究结果和回归模型的意义。在多元线性回归中，通常对连续变量采用t检验或方差分析，对于分类变量中的有序分类变量即等级变量采用秩和检验、无序分类变量采用卡方检验进行单因素分析，logistic回归也是一种线性回归，在实际应用过程中，经常会有研究者将有序分类变量当做无序分类变量进行卡方检验，这种做法是不可取的。例如某研究在探讨颅脑术后中枢神经系统感染的危险因素及护理对策时，将脑室外引流管分为3个等级，采用卡方检验对比其中枢神经系统感染的发生风险，见表2，虽然P<0.05，但结果并不可信；正确的做法应该是将数据作为等级资料进行秩和检验，或者进行单因素logistic回归。

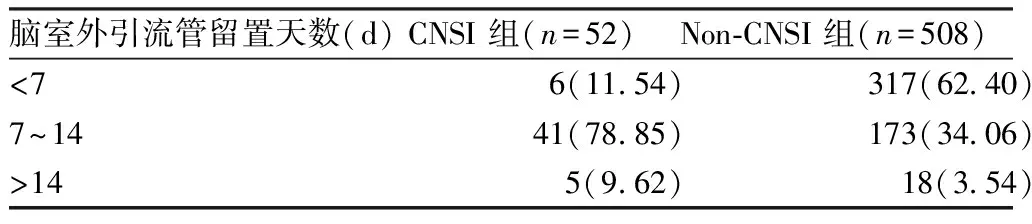
表2 颅脑术后患者中枢神经系统感染(CNSI)的脑室外引流单因素分析

logistic回归是一种特殊的线性回归，因变量为转换之后的logitP，而并非原始因变量P，筛选后的自变量需与logitP存在线性关系；因此适用于多元线性回归的自变量筛选方法并不完全适用于logistic回归，所以在进行多因素分析前需采用单因素logistic回归对变量进行筛选，χ2检验的结果可以与单因素logistic回归的结果互换[6]。而对于连续变量，很多研究采用t检验进行变量筛选，虽然大多数情况下t检验和单因素logistic回归的结果是相同的，但例外的情况也不少见；如表3数据所示，调查年龄是否为某病的危险因素时，使用t检验和单因素logistic回归进行变量筛选的结果并不相同(检验水准α=0.05)，有兴趣的读者可以进行验证。因此对于连续变量的筛选应采用单因素logistic回归，而不是对其进行均数比较。一言以蔽之，存在均数差异不代表自变量与logit P存在线性相关关系，尤其是对于多组连续变量的数据。

表3 某病的发病情况与年龄的数据资料

2.3自变量的独立性 在线性回归中自变量之间必须是相互独立的，如果自变量之间存在相关关系，就可能出现共线性问题。共线性是指线性回归模型中的自变量之间由于存在精确或高度相关关系而使模型估计失真或难以估计准确，即导致回归结果不可靠。因此在进行线性回归之前必须要进行共线性诊断。目前通用的方法是采用最小二乘法对共线性进行估计，用相关系数矩阵和方差膨胀因子(Variance Inflation Factor,VIF)评估共线性强度，若VIF>10说明两个变量之间存在较强共线性，不能直接进行回归分析。共线性的评估不只是数字间的联系，在进行共线性诊断之前首先要利用专业知识在逻辑上对自变量进行识别。目前绝大多数护理研究的logistic回归中都未曾提及共线性问题，但很多研究的自变量间存在明显的逻辑上的相关关系。例如某研究在探讨糖尿病前期的危险因素时，自变量中的BMI与腰围、年龄和三酰甘油浓度，文化程度和工作体力强度都可能存在共线性问题(见表4)；但研究并未提及共线性诊断的相关内容就将其全部引入logistic回归，其合理性有待商榷；更合理的做法是对自变量进行共线性诊断，如果不存在较强相关性再进行多因素logistic回归，如果存在较强共线性，则需在进行多因素logistic回归前删除其中一个引起共线性的自变量。除了删除自变量外，共线性问题还可以通过主成分分析、Lasso回归等方式解决[7]。

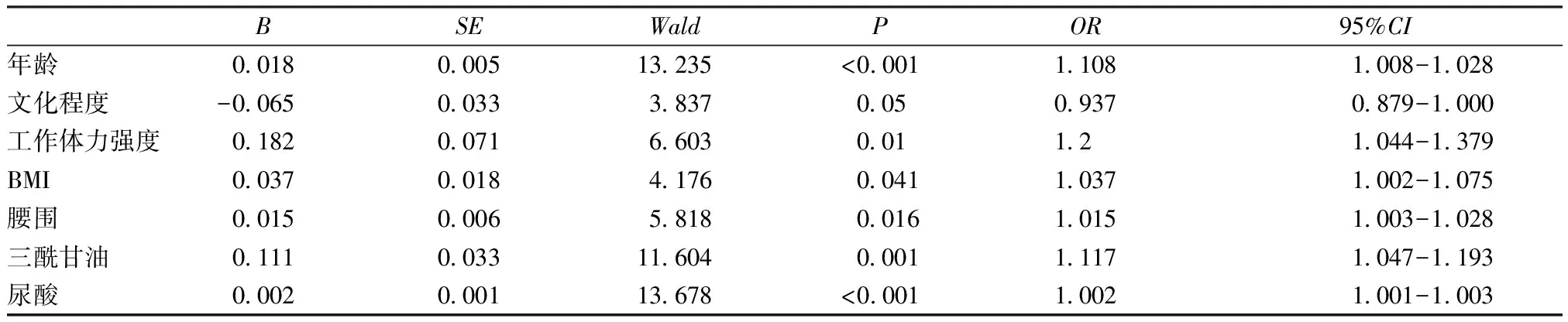
表4 糖尿病前期危险因素的logistic回归分析结果

2.4变量赋值 变量赋值与logistic回归结果的解释息息相关。logistic回归中通常以赋值较小的变量为参照水平，虽然二分类变量的赋值不会对logistic回归的结果产生影响，但有序分类变量和哑变量的设置则不然；为了更好的解释分析结果，得出正确结论，必须在文章中说明变量赋值情况，尤其是因变量的赋值，变量赋值地混乱容易产生错误的结论，一旦出现研究结果与研究结论不一致的情况将大大降低研究结果和结论的可信性。某研究在探究产褥期盆底功能障碍患者盆底肌锻炼依从性的影响因素时，经过单因素分析后将年龄、受教育程度、盆底肌功能锻炼认知程度、盆底肌功能受损程度、睡眠障碍、护理人员专业指导、家庭支持等因素纳入多因素分析，赋值情况，见表5，多因素分析结果，见表6。最后得出结论：受教育程度高、盆底肌功能锻炼认知程度高是盆底肌锻炼依从性的保护因素，盆底肌功能受损程度轻度、有睡眠障碍、无护理人员专业指导、无家庭支持是盆底肌锻炼依从性的危险因素(P<0.05)。但该作者在文中并未提及对因变量的赋值，因此在解释结果时会给读者带来很大的困扰；假设作者将依从赋值为1，不依从赋值为0，将得出有睡眠障碍、无护理人员专业指导、无家庭支持是盆底肌锻炼依从性保护因素的结论；假设作者将依从赋值为0，不依从赋值为1，将得出受教育程度高、盆底肌功能锻炼认知程度高是盆底肌锻炼依从性的危险因素，盆底肌功能受损程度轻度是盆底肌锻炼依从性的保护因素的结论，无法得出作者在文中得出的结论。研究结果与研究结论不一致的情况是每一个护理研究者都必须要避免的。

表5 纳入变量及赋值

表6 多因素分析结果

3 参数的解释

3.1回归系数β 参数β0是常数项，表示模型中所有自变量均为0时，logit P的值，我们可以将其理解为未纳入回归模型的未知因素对因变量的影响效应；β1，β2…βm是回归系数，表示在控制其他自变量时，自变量变化一个单位引起的因变量的变化。值得注意的是logistic回归的因变量为logit P而并非概率P的变化，因为量纲的不同我们在比较自变量对模型的贡献大小时，不能直接使用回归系数β，而应该使用标准化回归系数进行比较。

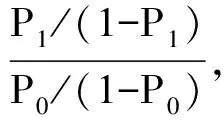
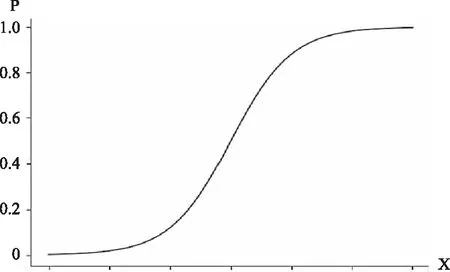
图1 logistic回归曲线

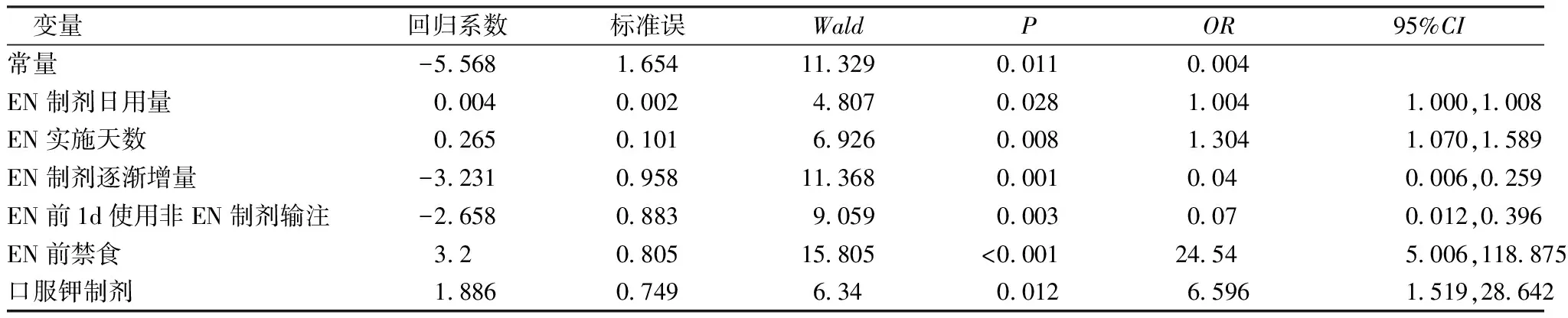
表7 ICU患者EN期间腹泻相关因素的多因素分析

logistic回归虽然是线性回归，但因变量的转化使得回归结果的解释不再像多重线性回归那么直接；因此要对logistic回归的结果做出正确合理的解释就要求研究者对logistic回归的基本原理有更深入的理解。

4 拟合优度的评价问题

对回归模型的假设检验只是验证了回归模型和回归系数是否具有统计学意义，但无法对回归模型的拟合效果进行评价。如果研究仅限于发现或验证影响因素，尚可不进行拟合优度评价；但要想说明已建立的回归模型对实际情况的拟合效果，就必须对所拟合的模型进行评价，即评价模型的预测值是否与观测值具有较高的一致性。这就是拟合优度检验问题，尤其是在应用logistic回归进行模型预测的时候。但目前为止几乎没有护理研究对logistic回归的拟合优度进行评价和说明，拟合优度检验是 logistic 回归分析过程中不可缺少的一部分，拟合效果良好，所做出的结论才更符合事实；若拟合效果不好，预测值与实际值差别较大，得出的结论就是不可靠的。logistic 回归的拟合优度可以通过似然比检验、Hosmer-Lemeshow检验、Cox & SnellR2系数、NagelkerkeR2系数、错判矩阵等方法进行评价[9]，在似然比检验、Hosmer-Lemeshow检验中，当P>0.05表示模型拟合度较好；Cox & SnellR2系数越接近1，拟合度越好，而NagelkerkeR2系数是Cox & SnellR2系数的调整值；错判矩阵是指模型预测值与实际值相符的比例，比例越高拟合度越好。实际应用中需根据具体情况选择合适的评价方法。

统计方法的学习首先是思想和理论的学习，然后才是软件操作。logistic回归模型的建立较为复杂，受到多种因素的限制，除了上文提到的问题还有像数据缺失问题、失访问题以及特殊样本问题等；因此，在应用中需要格外注意其适用条件，回避常见错误。