人行悬索桥软颤振特性风洞试验研究
2022-11-09刘雪猛冉芸诚
刘雪猛, 冉芸诚, 李 强
(西南交通大学, 四川成都 610031)
近年来,越来越多景区开始建造玻璃景观人行桥来吸引游客,桥面高程也在不断提高,而人行桥主梁断面一般为钝体断面,高风速下易发生破坏性较强的颤振现象,为确保人行桥的正常使用,有必要对其抗风性能的进行深入研究。
目前已有学者开展了人行景观桥颤振性能的研究。2009年,许福友等[1]对宿迁黄河公园人行景观桥在不同风场、不同攻角下进行了风致响应分析,试验证实了其气动稳定性。2012年,白桦等[2]对人行悬索桥抗风性能改善措施进行了研究,得出增设抗风缆和上中央稳定板都可提高其颤振性能的结论;2017年,何恺等[3]分析了跨度430 m的人行悬索桥的颤振性能,其结果表明:提高桥梁重量并增设抗风缆能很好地提升其颤振稳定性;2018年,魏志刚等[4]详细分析了抗风缆不同锚固位置对人行悬索桥颤振的影响,结果表明:仅在跨中施加抗风缆就能显著提高桥梁结构的固有频率,从而提高颤振性能。综上的这些研究和措施能有效抑制有明显发散临界点的“硬”颤振。
除了这些极具破坏的发散性“硬”颤振现象外,国内外学者在节段模型风洞试验中发现,越来越多的钝体桥梁断面在达到起振风速后,并未表现出明显的发散性颤振,而是呈现为在不同风速下均具有不同的稳态振幅,且振幅随着风速的增加而缓慢增大[5-6]。这种表现出明显非线性特征的颤振现象被学界称为“非线性颤振”或“软颤振”。Chen等[7-8]研究了软颤振现象与颤振导数的关系;张朝贵[9]提出了一种非线性气动力模型较好地解释了软颤振现象;朱乐东等[10]分析了4种典型桥梁断面的软颤振现象,并讨论了影响软颤振振幅的几种因素;郑史雄等[11]对π型断面主梁软颤振特性及抑振措施进行了研究;王骑等[12]研究了大跨桥梁颤振后状态的气动稳定性;董佳慧等[13]研究了边箱钢-混叠合梁的软颤振特性,并给出了不同气动措施对颤振性能的影响;伍波等[14]对双层桥面桁架梁进行了风洞试验研究,详细分析了其软颤振特性。目前鲜有针对人行悬索桥软颤振的研究,而钝体特性较为显著的人行桥主梁断面发生软颤振现象的可能性较高,尽管软颤振并不会导致桥梁断面发生损毁,但其较大的自限幅振动对于游客的安全性和舒适性影响较大,因此需着重研究该类桥梁的软颤振现象及特性。
本文以西藏·八宿·怒江72拐峡谷玻璃吊桥为研究对象,通过节段模型自由振动试验,从软颤振振幅大小、软颤振频率、弯扭耦合运动相位差、竖向振动参与度等方面对其原始设计断面进行了颤振特性分析,对比了该人行桥断面与其他形式断面在软颤振特性上的异同;分析了水平导流板对颤振特性的影响,得出不同攻角下不同工况的软颤振临界风速并进行初步分析。本文研究可为后续同类型桥梁的软颤振性能的研究提供参考。
1 节段模型风洞试验
1.1 工程概况
西藏·八宿·怒江72拐峡谷玻璃吊桥是位于西藏省的一座景观人行桥,为提高主梁的抗风结构稳定性,在主梁下方两侧设置抗风缆。桥梁设计主跨为 152 m,桥面净宽2 m,桥面铺设超白钢化夹胶玻璃。人行桥的桥面自重及桥面活载通过主索传递至两侧的锚碇,依靠两侧锚碇保持桥体的抗倾覆稳定性。人行桥主视图如图1所示,主梁标准横断面如图2所示。
1.2 节段模型试验参数
本文的风洞试验研究在西南交通大学XNJD-2 直流式风洞开展,风洞试验段截面高度为1.5 m,宽度为1.3 m,风速范围1.0~20.0 m/s(表1)。
根据风洞断面尺寸、阻塞率及试验相关要求,制作了缩尺比1∶8的节段模型,模型长L=1.1 m,宽度B=0.375 m,高度H=0.21 m。附属结构采用ABS塑料板制作并确保外形及透风率相似,模型由8根拉伸弹簧悬挂,并在模型两端设置端板,保证流动的二维性,形成可竖向运动和绕模型扭心转动的二自由度振动系统,如图3所示。通过给定大振幅激励,获取自由衰减振动位移时程,由式(1)、式(2)可计算出该动力系统的频率和阻尼比。具体试验参数列于表1所示。扭弯频率比实桥值与模型值之间的误差小于4%,满足试验要求。由于颤振由扭转模态主导,故以扭转频率计算实桥与模型的风速比,其值为2.66。

图1 人行桥(单位:cm)
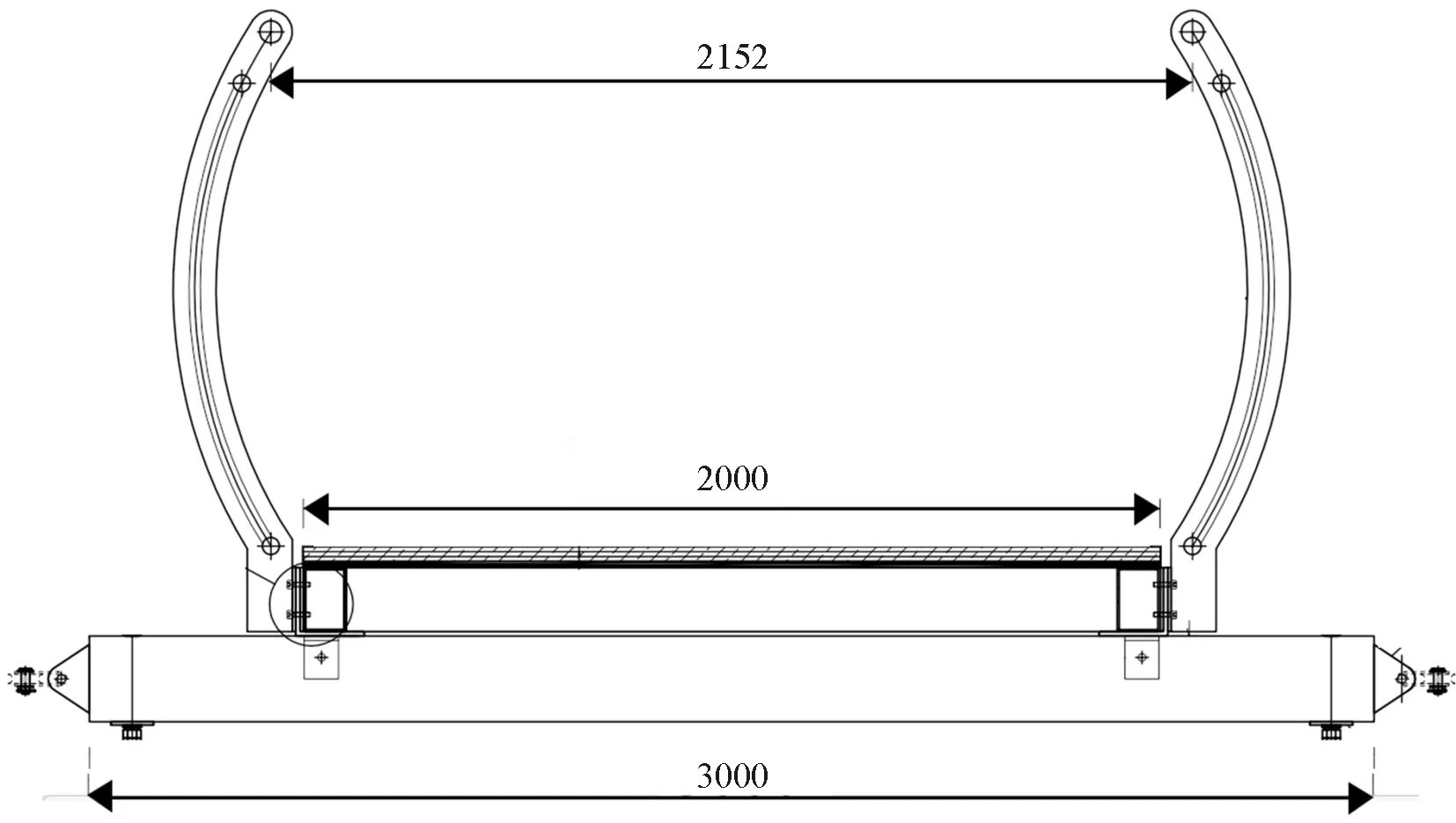
图2 原始主梁横断面示意(单位:mm)

表1 节段模型试验动力参数

图3 弹簧悬挂节段模型
(1)
(2)
式中:f为频率,ζ为阻尼比,yn、yn+m为相隔m个周期的2个波峰振幅值;tn、tn+m分别为2个波峰对应的时间。
2 原始断面软颤振现象
试验测试了断面在5种风攻角(0°、±3°、±5°)下的颤振性能,试验来流为均匀流,对未加气动措施的原始断面进行节段模型颤振试验。
图4给出了不同攻角下人行桥竖向及扭转振幅RMS(Root Mean Square)值随风速变化的关系。由图可以看出:随着风速的增加,断面并未有明显的颤振发散临界点,而是在达到起振风速后表现出振幅稳定的非线性颤振现象,即“软颤振”。相同来流风速时,不同攻角下的软颤振振幅大小差异明显,振幅随着攻角的增大(-5°~5°)而增大。
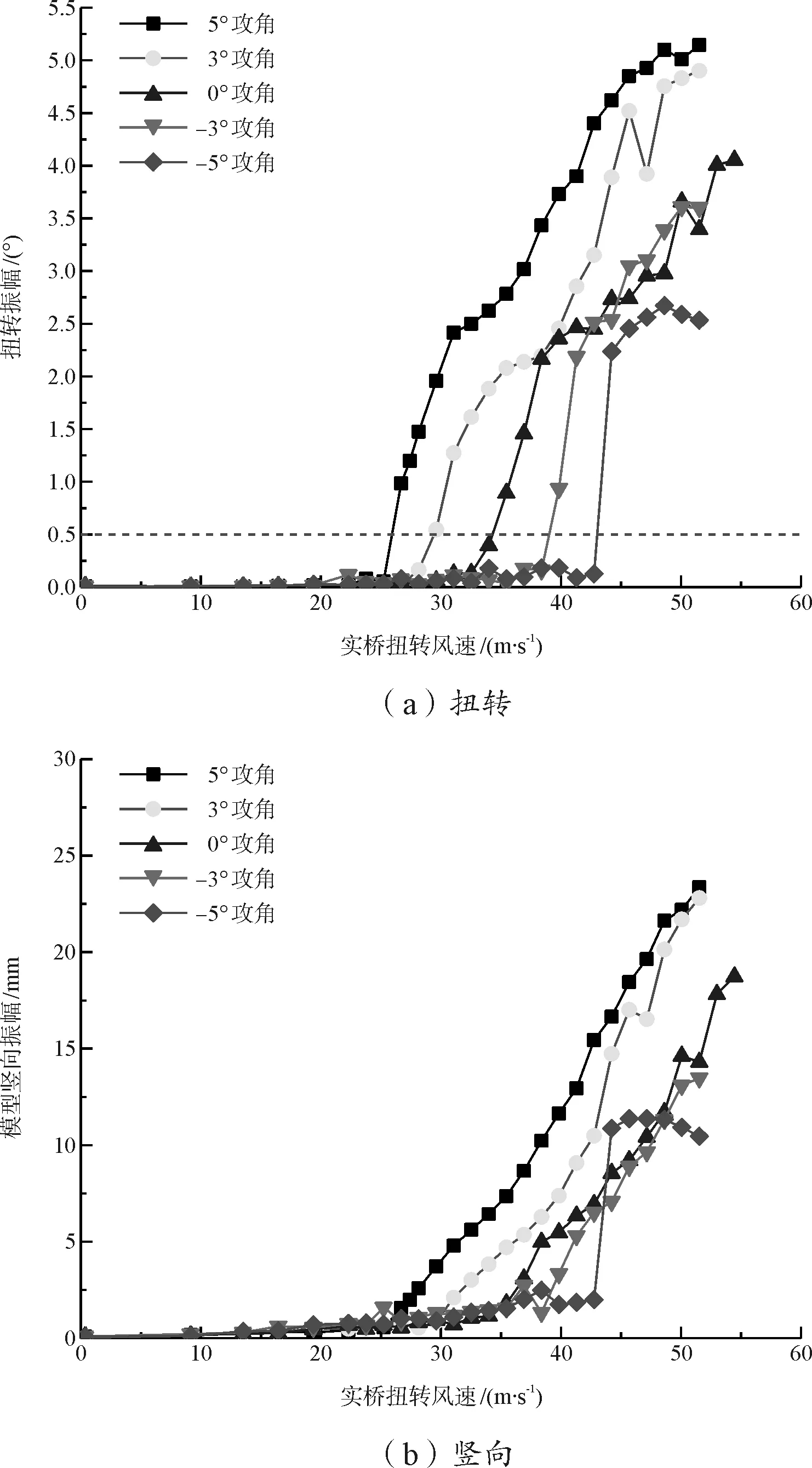
图4 软颤振振幅RMS值变化
由于软颤振没有明显的发散临界风速,此处参照桥梁抗风规范[15]中扭转振幅RMS值0.5°时所对应的来流风速为“软颤振临界风速”。由图4可知,不同风攻角下的软颤振临界风速存在明显差异:随着风攻角由-5°至 5°,软颤振临界风速逐渐降低, -5°风攻角下软颤振临界风速最大,为44.23 m/s,+5°风攻角下软颤振临界风速最小,为26.68 m/s;竖向振幅与扭转振幅大小随风速增长的变化趋势较为类似,高风速下断面呈现典型的弯扭耦合运动。
为便于观察弯扭耦合运动过程中竖向和扭转振幅的大小,此处以弧度表示扭转无量纲振幅,竖向无量纲振幅定义为arctan(h/B),其中h为模型竖向振幅,B为模型宽度。以+5°风攻角实桥扭转风速51.54 m/s为例,绘出扭转和竖向无量纲位移响应时程曲线如图5所示。由图可知,扭转无量纲振幅高于竖向无量纲振幅,但竖向振动也有较大的参与;并且位移响应几乎同时达到峰值,可见两者的运动相位差很小。

图5 扭转和竖向无量纲位移响应时程
为进一步分析人行桥的颤振特性,对不同攻角下各个风速的颤振时程数据进行快速傅里叶变换,从而获得其频域特性,图6给出了软颤振发生后,不同风攻角下软颤振竖向、扭转频率随风速的变化曲线,由图可知:扭转频率与竖向频率始终在数值上保持相同,这一特性与以往学者对于软颤振频率的研究结果一致;对于同一风速不同风攻角,软颤振频率则存在明显差异,随着风攻角由-5°至5°,软颤振频率由大变小;除-5°风攻角下频率随风速的增大而增大外,其余攻角下频率均随风速增大而减小,人行桥正攻角下的频率变化规律与文献[14]中的桁架梁一致,对于人行桥-5°攻角下频率随风速增大而增大这一现象还有待进一步做颤振机理的研究;模型系统的固有扭转频率为2.271 Hz,软颤振频率变化整体上围绕在系统的固有扭转频率附近,其中正攻角下软颤振频率低于系统固有扭转频率,负攻角下软颤振频率高于系统固有扭转频率。
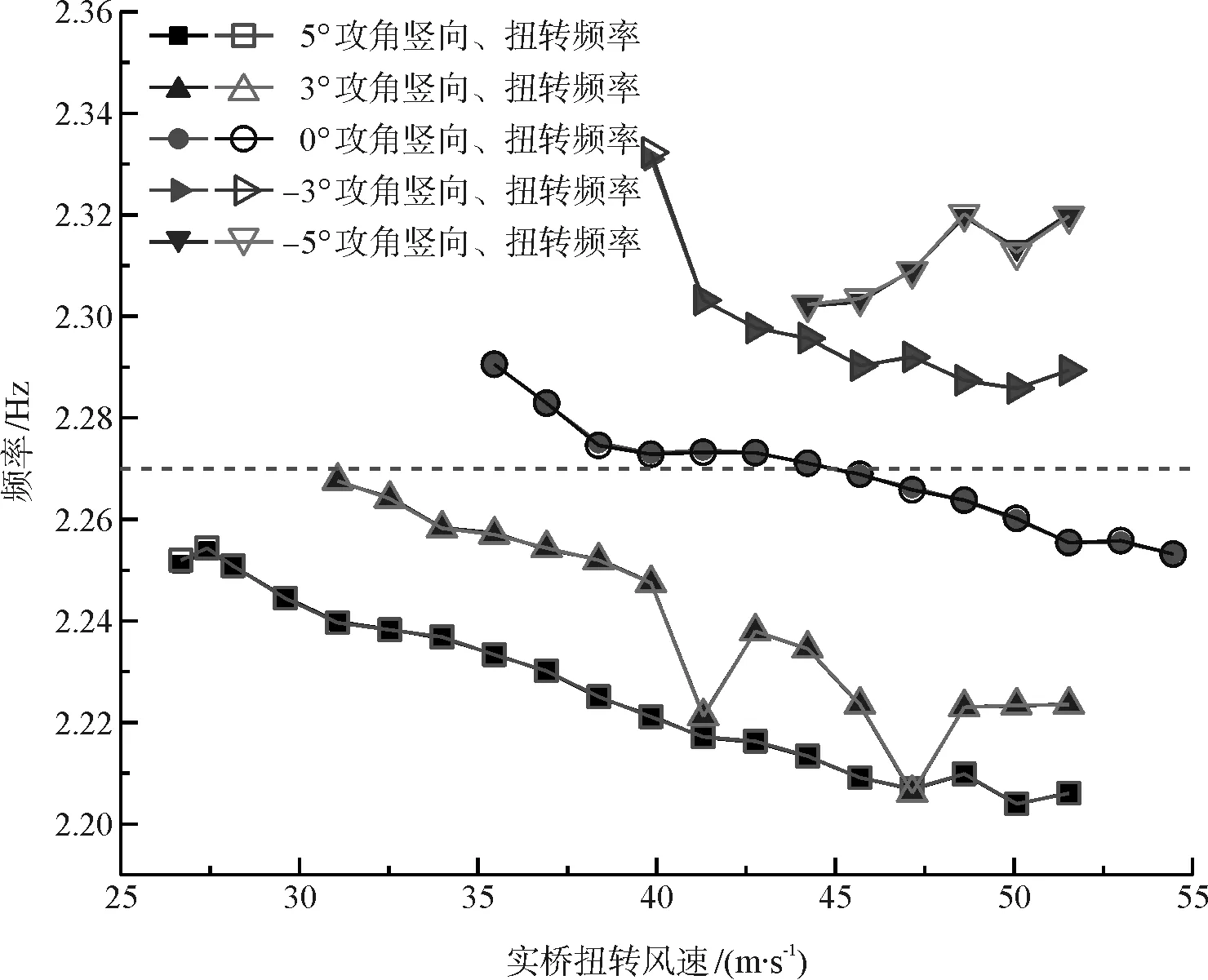
图6 软颤振频率变化曲线
接下来详细分析竖向运动与扭转运动相位差大小、相位差随风速的变化关系,对于弯扭耦合振动,竖弯运动方程与扭转运动方程可写为:
h=h0sin (ω1t+θ1)
(3)
α=α0sin (ω2t+θ2)
(4)
式中:h0、α0分别为竖向运动振幅、扭转振动振幅;ω1、ω2分别为竖向振动圆频率、扭转振动圆频率;θ1、θ2分别为竖向振动初始相位角、扭转振动初始相位角,θ1-θ2即为相位差。
为清晰地看出相位差随风速的变化规律,图7给出不同攻角下相位差随风速的变化曲线,由图7可知:不同风攻角下相位差的变化规律存在明显区别,3°、5°攻角下随风速的增大相位差先由11.3°先减小为0°附近,而后开始增大到7°左右,两者变化规律类似;0°攻角下随风速的增大相位差由0.74°逐渐增大到7.69°;负攻角下的相位差明显大于正攻角,其中-5°攻角下的相位差最大;-3°攻角下随风速的增大相位差由27.9°减小为17.1°;-5°攻角下随风速的增大相位差由44.13°减小为33.13°;人行桥软颤振负攻角下存在明显的相位差,为典型的弯扭耦合振动,正攻角下相位差相对较小,5°攻角、风速41.3 m/s时相位差几乎为0°,此时的振动形态可认为偏心扭转振动。

图7 相位差随风速变化曲线
为了较直观地看出竖向振动参与程度随风速增长的变化趋势,用竖向振动无量纲振幅除以扭转振动无量纲振幅,即振幅比来描述。振幅比越大表示竖向参与程度越高。图8为不同攻角下振幅比随风速的变化曲线,由图可知:不同攻角下振幅比的整体变化趋势是相同的,都随风速的增大而增大;其中正攻角下的竖向振动参与度高于负攻角下的参与度,-5°下的振幅比明显低于其他攻角。
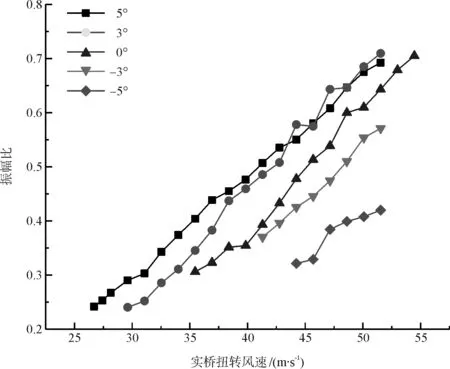
图8 振幅比随风速变化关系
3 导流板对软颤振的影响
参考传统的线性颤振抑振措施,并考虑桥梁的美观及气动措施设置的便利性,采用断面两侧增设水平导流板的方式(图9),模型导流板宽度4.2 cm,宽度刚好与下横梁齐平,具体措施如图10所示。人行桥在不同攻角下扭转振幅RMS值风速变化如图11所示,由图可知:安装导流板后,与图4(a)相比0°、3°、5°的3个攻角下的软颤振起振风速增大,而-3°、-5°的2个攻角下的软颤振起振风速减小,-5°攻角起振风速最小,只有23.76m/s;起振后0°、-3°、-5°的3个攻角下的扭转振幅迅速增大,振幅增大到4°后增长速度逐渐缓慢;5°攻角下扭转振幅始终保持在较低值。

图9 水平导流板
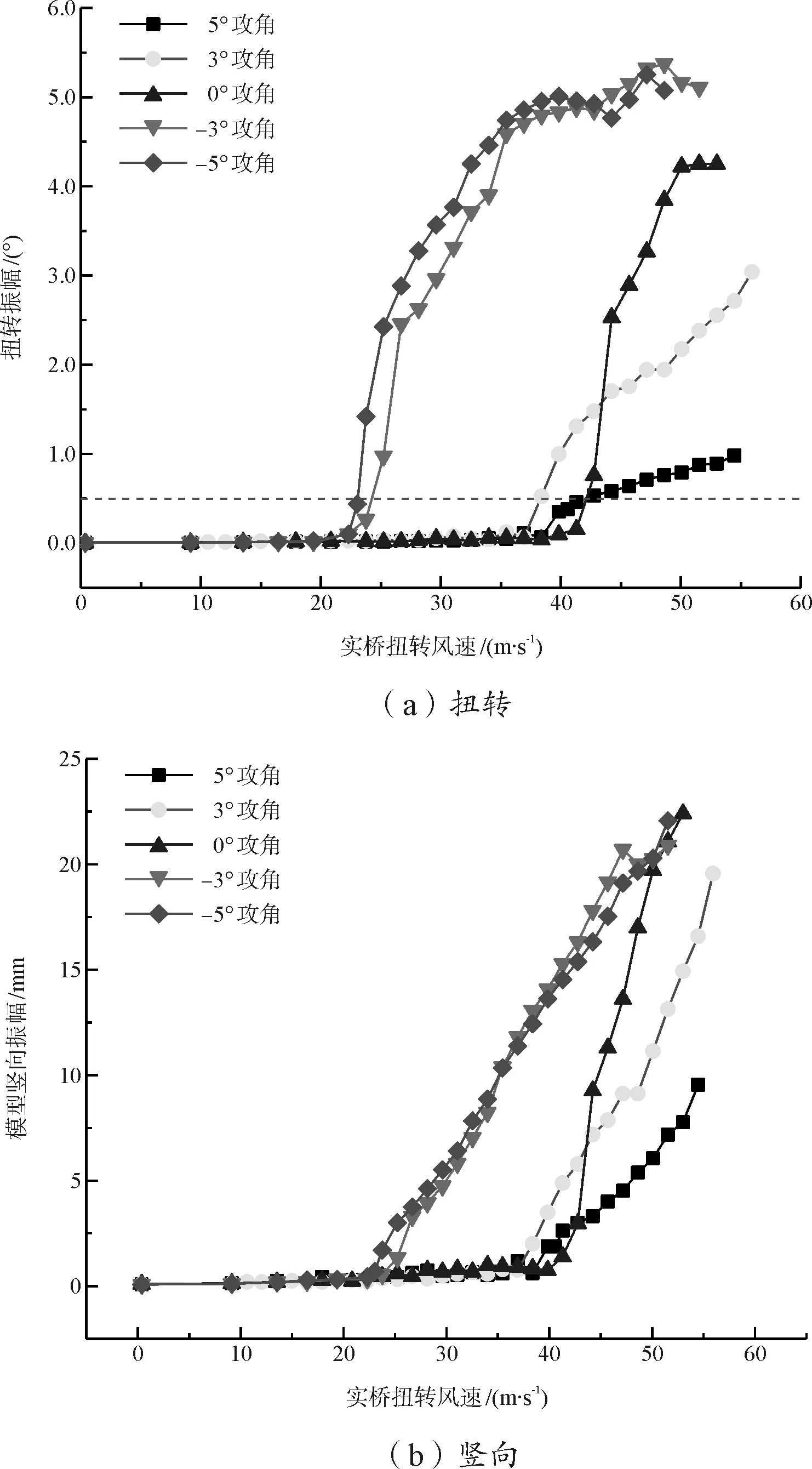
图10 软颤振振幅RMS值变化图
进而分析安装导流板措施后对软颤振频率的影响,图11给出了软颤振发生后,不同风攻角下软颤振竖向、扭转频率随风速的变化曲线,由图可知:从数值大小上看,软颤振频率整体小于系统固有扭转频率2.271 Hz;从变化趋势上看,正攻角和零攻角下频率随风速增大而减小,负攻角下变化趋势为先减小后增大,整体维持在较大值,其中-5°频率大于-3°频率。对比图6可知导流板措施使负攻角下的频率发生明显改变,数值上整体降低并且变化趋势也发生了改变;对正攻角的改变不显著。
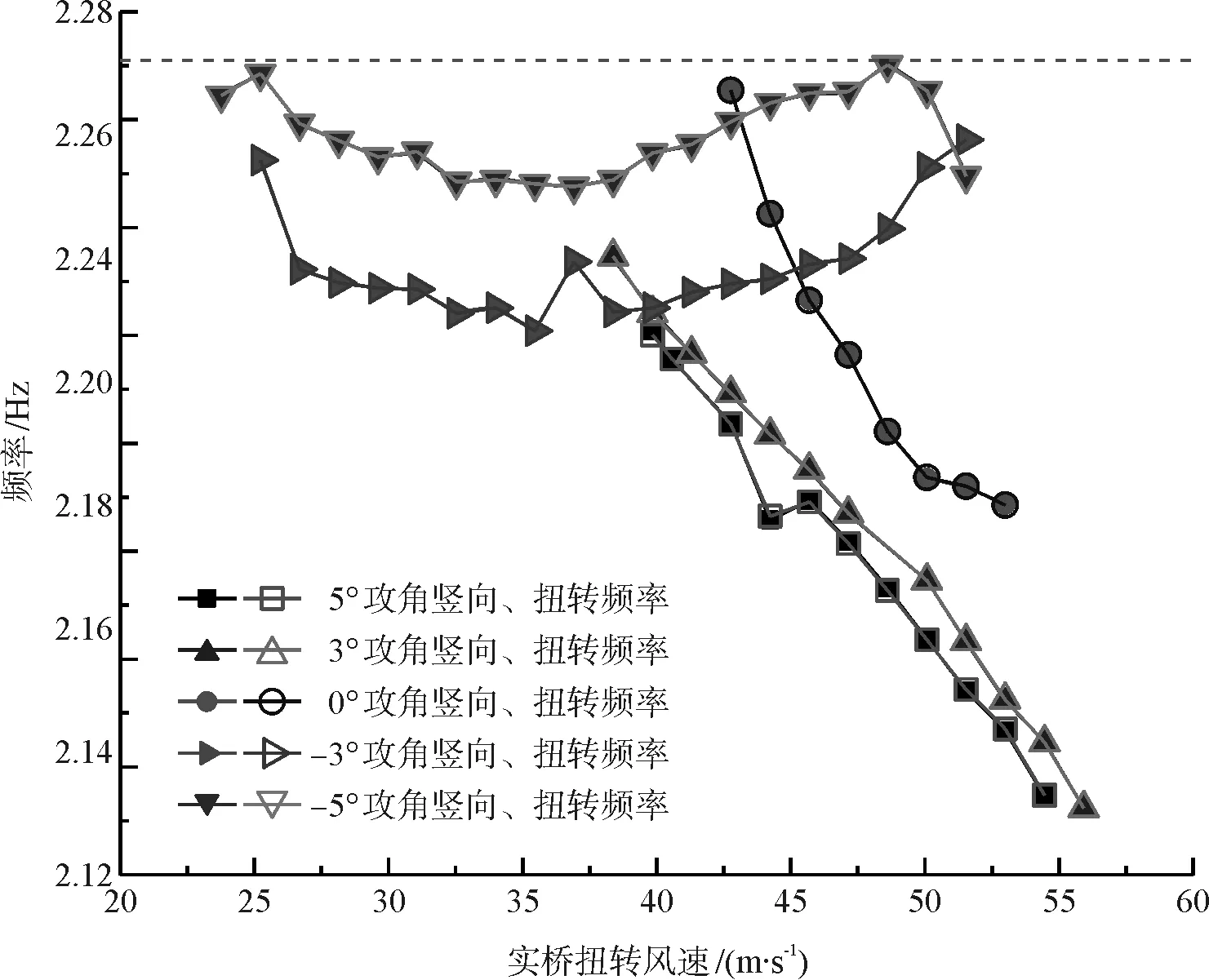
图11 软颤振频率变化曲线
图12为安装导流板后相位差随风速的变化曲线,与图7相比,均是负攻角下的相位差明显大于正攻角,其中-5°攻角下的最大;但导流板的安装使其变化趋势发生了改变:不同攻角下,相位差随风速的增大均是增大趋势,与原始断面变化趋势存在明显差异。
从振幅比的变化关系图13中可以看出:振幅比仍是随着风速的增大而增大,但导流板的安装使不同攻角的差异减弱,-5°攻角下的振幅比有了明显的增大。
综上所述,此导流板措施使人行悬索桥正攻角的软颤振临界风速大幅度提升,但降低了负攻角下的软颤振临界风速;降低了负攻角下的软颤振频率,使其低于了系统固有扭转频率;降低了负攻角下的相位差,并改变了其随风速的变化规律;增大了负攻角下竖向振动参与度,尤其是-5°。
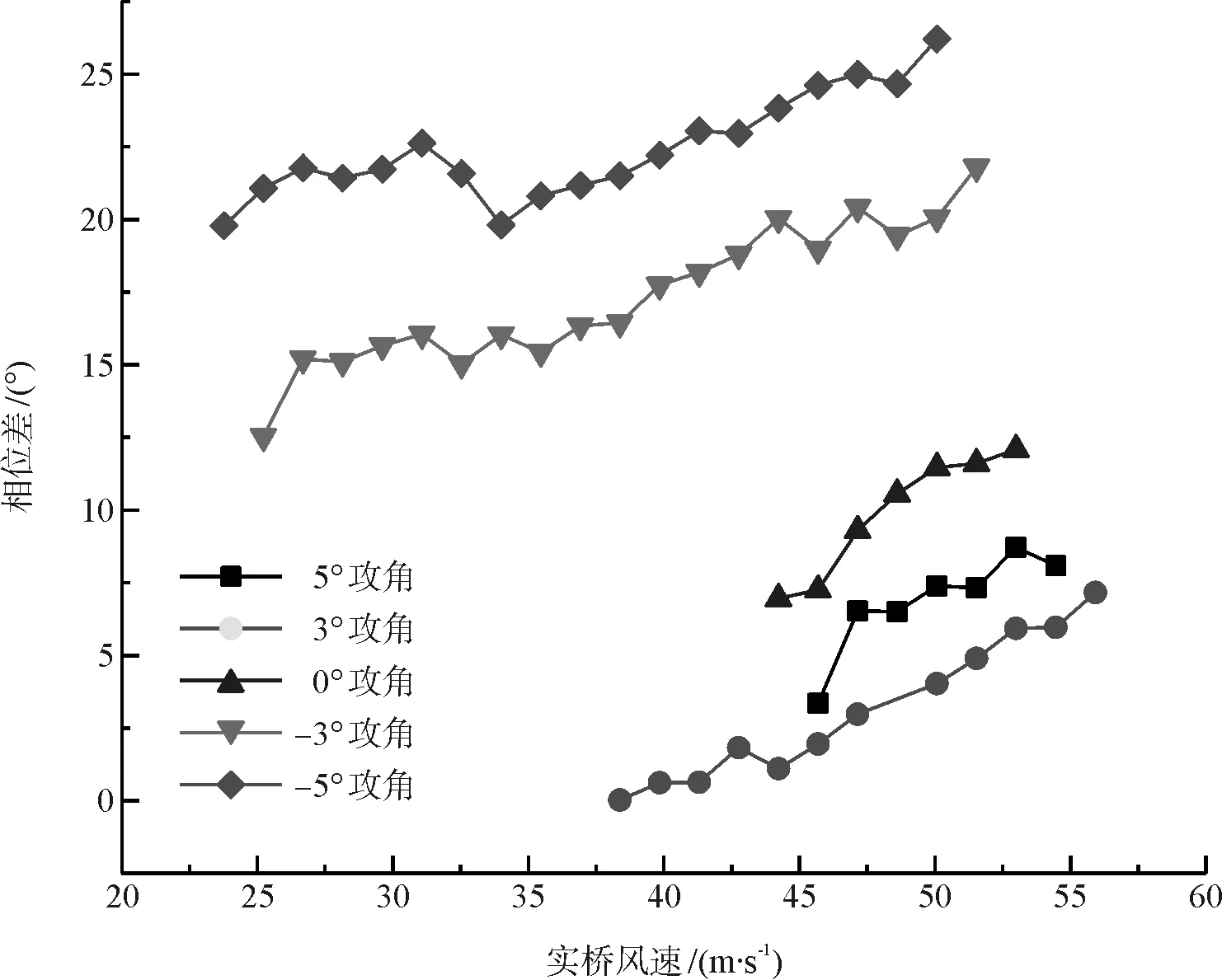
图12 相位差随风速变化曲线
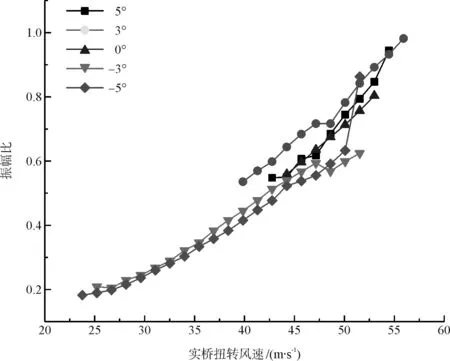
图13 振幅比随风速变化关系
4 结论
利用节段模型风洞试验,详细分析了人行悬索桥的软颤振特性及水平导流板的作用,主要结论:
(1)人行悬索桥呈现典型的软颤振形态,即给定风速下,振动频率单一且振幅稳定。
(2)不同风攻角下人行悬索桥软颤振临界风速差异性很大,-5°攻角时临界风速44.23 m/s,+5°只有26.68 m/s。
(3)软颤振发生时,竖向与扭转振动频率相同,随风速的增加,颤振频率减小(-5°攻角下数据点少,不明显);负攻角下振动频率大于模型固有扭转频率,正攻角下振动频率小于模型固有扭转频率。
(4)负攻角相位差明显大于正攻角,耦合振动形态显著。
(5)对于人行悬索桥来说,水平导流板会大幅度增加正攻角下的颤振临界风速,但会降低负攻角下的颤振临界风速。
