底部加热肥皂泡上准二维湍流的数值模拟*

贺啸秋，熊永亮，徐 顺，彭泽瑞，陈 波

（华中科技大学 航空航天学院 力学系，武汉 430074）

引言

湍流运动广泛存在于自然界中，从星系中的星际介质运动，到杯子中被搅拌的咖啡流动，虽然时空尺度差距悬殊但都属于湍流流动[1].流体的湍流运动对传热传质具有重要的影响[2].当湍流流场中流体的运动仅具有两个独立的空间自由度时，称之为二维湍流[3-6].相比三维湍流，二维湍流的结构更易于观察与分析，且在直接数值模拟（DNS）所需要的计算资源显著减小的同时又保留着湍流的许多关键特征[3].另一方面，二维湍流并不是三维湍流进行简单维度压缩的结果，它也具有与三维湍流完全不同的显著差别[3].其中最核心的差别是最早由Kraichnan[7]、Leith[8]和Batchelor[9]发现的反向能量串级，即在充分发展的二维湍流中，在特定尺度范围内存在着能量从尺寸较小的涡向尺寸较大的涡反向传递的现象.在研究海洋或者大气中的大尺度运动时，海洋或大气的侧向尺寸远大于高度方向的尺寸，在研究较大尺度的流动问题时可以忽略掉流体在高度方向的运动而作二维流动处理[10-11].因而，在地球物理与行星物理学中，二维湍流具有重要的研究价值[12].

严格意义下的二维湍流在实验室或自然界中并不存在[3]，研究二维湍流主要依赖于DNS[3]或者在实验条件下借助肥皂膜及电磁力抑制形成准二维流动[13].众所周知，肥皂薄膜的厚度只有数微米，但其侧向尺寸可以达到数十厘米以上，肥皂薄膜被广泛用于准二维湍流实验[12].Kellay[13]在实验中研究了加热肥皂泡中的准二维湍流.实验中一个半球形的肥皂泡被固定在基座上，基座以水浴的方法对肥皂泡底部进行加热，肥皂泡上的流体在浮力的驱动下形成复杂的湍流运动[14-15].肥皂泡上的流体运动与大气流动都具有准二维流动特征，且具有相似的几何特征，这使得学者以肥皂泡为简化模型开展了大气流动中尺度结构特征的研究[13-19].热带气旋是大气中的一种特殊中尺度结构，对人类社会具有重要的影响，是多种极端天气与自然灾害的直接原因[10].Seychelles 等[14]在实验中观察到肥皂泡上出现了能长时间独立存在的岛涡，岛涡的运动规律与大气中的热带气旋类似，都具有超扩散的特征[14,16].此外，岛涡的强度随时间变化的规律与大气中的热带气旋类似[15].基于这些特点，Meuel 等[17]基于肥皂泡上岛涡与飓风的运动特征提出了预测大气气旋运动轨迹的模型.在湍流方面，研究者们发现肥皂泡上的流动具有其特有的曲面准二维热对流特征，通过实验与DNS，可利用这一标准模型开展湍流流动机理的研究与湍流理论的考察[16,19-21].例如通过对肥皂泡的旋转，发现了旋转效应产生了新的温度小尺度脉动标度关系[18].因而研究肥皂泡上的湍流热对流不仅具有重要的应用价值，同时也可以拓展与丰富学界对湍流物理机制的认识.

借助赤平极射投影法，Xiong 等[20]首先实现了具有半球面几何的二维流场DNS.他们计算了Rayleigh 数为1×108的肥皂泡流场，由于缺乏能量耗散，所得到的计算结果并不稳定[20].Meuel 等[15]通过实验研究了肥皂泡上的漩涡结构特征，并与DNS 计算结果进行了对比，发现两者符合得较好.此后，Bruneau 等[19]在DNS 代码中引入了能量耗散项，使得计算得到的流场能够达到统计稳态，计算获得的流场与实验观察到的肥皂泡上的流动具有相同的特征，同时还发现DNS 计算结果对一定的外部耗散并不敏感，他们还通过DNS 结果发现了肥皂泡对流具有Bo59标度律，这与实验中肥皂泡上观察到的结果一致.最近，Meuel 等[18]同时使用实验与DNS 方法研究了旋转肥皂泡上的温度脉动，他们的研究中实验与DNS 获得了非常相近的结果.经过近十年的发展，肥皂泡上热对流的DNS 已日趋成熟，相比实验方法，使用DNS 研究肥皂泡上的湍流热对流也展露出较大的优势.首先，目前的实验手段在获得肥皂泡上的空间特征结构关联上还具有一定难度，难以同时测量整个流场[13-14,17].对肥皂泡上的准二维湍流的深入研究有必要获得包含全部尺度特征的完整流场信息，而采用DNS 方法可以满足这一需求[22].其次，实验方法也难以精确地在曲面几何中测量如能量级串、结构函数等湍流的小尺度特征[23-24].而DNS 获得的流场包含全部尺度的特征，可以使用编程后处理的方法高效快捷地计算湍流的小尺度特征.另外，使用DNS 方法可以方便地在更大、更明确的参数空间内研究肥皂泡曲面空间上的热对流，并规避了如非Boussinesq 效应、不均匀加热边界、材质与外界扰动等实验中常见的误差来源.本文将详细介绍这一套简便求解肥皂泡上流场的并行计算DNS 方法，以及针对球面二维湍流的分析方法.

文中通过该方法对多个高Rayleigh 数下的热对流开展了DNS，并探索了肥皂泡上的湍流双级串现象与小尺度脉动的标度关系.

1 模型介绍与控制方程

本文研究的是在底部加热的半球形肥皂泡上的准二维湍流.肥皂薄膜的厚度远小于肥皂泡的半径R，可以忽略流体在肥皂薄膜厚度方向的运动，使用二维半球面来近似肥皂泡的几何外形.赤道是肥皂泡与基座接触的边界，几何外形为一个半径为R的圆周.首先，需要建立坐标系描述肥皂泡上流体微元的空间位置.三维直角坐标系Oxyz以二维半球面的球心O为原点，ex，ey和ez分别为x，y和z方向上的单位基矢，其中ez方向与重力方向相反.在直角坐标系下，肥皂泡用曲面方程x2+y2+z2=R2(z≥0)描述，赤道的曲线方程为x2+y2=R2.采用球坐标系Orϕθ，其中r≡R可方便地将该问题简化为二维，球坐标系的单位基矢用er，eϕ和eθ表示.与球坐标类似，地理坐标系ϕ*Oθ*能更加直观地描述肥皂泡上任意一点的空间位置，经度定义为ϕ*=ϕ，纬度定义为θ*=90◦-θ.肥皂泡顶部纬度为 90◦（θ*=90◦）,而在赤道纬度为 0◦（θ*=0◦），地理坐标系的基矢为eϕ*=eϕ，eθ*=-eθ.对于肥皂泡上的速度场u有如下定义：

肥皂泡上流场的唯一边界是赤道，边界条件为恒温无滑移（T=T0,u=0）边界条件.若肥皂泡的初始温度远小于肥皂泡的赤道温度，随着时间的推进，在赤道附近的流体，通过赤道从外界吸收热量，使其温度升高密度降低.此时，流体在浮力的驱动下向肥皂泡顶部运动，肥皂泡中产生热对流.数值模拟中，Boussinesq 近似常被用来描述流体温度与密度的关系.当流体运动至远离赤道的位置时，热量向周围的低温空气扩散，导致温度下降密度逐渐上升，受到的浮力逐渐减弱.观察实验中的肥皂泡流场可以发现，由于肥皂泡既向冷空气散热又与冷空气产生摩擦，肥皂泡上的湍流热对流不断持续并达到了统计平衡态[13-18].为了使DNS 中肥皂泡进入统计平衡态，外冷却项ST和外摩擦项Fu被分别加入到能量方程与动量方程中，用于描述流体与环境冷空气的散热与摩擦，S为外冷却系数，而F是外摩擦因数.以往的研究表明，外冷却项和外摩擦项可以较好地描述肥皂泡与实验环境之间的能量交换[19-21].因此，流体在肥皂泡上运动的控制方程可写为Ra建立了流体受到的浮力与黏性力之间的一个关系，Pr则反映了动量传输及热量传输速率之比，对于特定的物质，Pr是流体本身的属性，此处为一定值.

考虑到需要在球坐标系下求解控制方程（4），则在肥皂泡的顶点处引入了奇异性.而在直角坐标系下无法对这一曲面进行二维描述，采用三维描述并进行离散则降低了曲面的光滑性.通过赤平极射投影法引入的投影空间坐标系x˜Oy˜可以规避以上全部缺点.首先，定义肥皂泡的顶点关于赤道平面的镜像点为B点，B点在无量纲直角坐标系Oxˆyˆzˆ中的坐标为(0,0,-1).令A点为肥皂泡上任意一点，存在唯一直线经过A点与B点，直线AB与赤道平面的交点为C，C点就是A点的赤平极射投影点.图 1 展示了赤平极射投影几何关系，其中橙色平面为赤道平面，A是肥皂泡上任意一点，B为肥皂泡顶点关于赤道平面的镜像点，C为投影点.投影坐标系Ox˜y˜的原点为肥皂泡的球心，x˜轴与xˆ轴重合，y˜轴与yˆ轴重合.由简单的几何关系可以推导出，无量纲的直角坐标系向投影空间的正变换is为

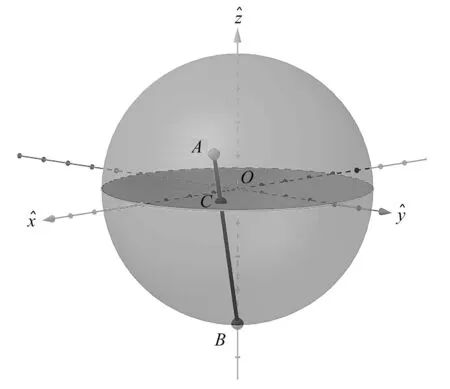
图1 赤平极射投影法示意图Fig.1 An illustration of the stereographic projection

而对应的逆变换为

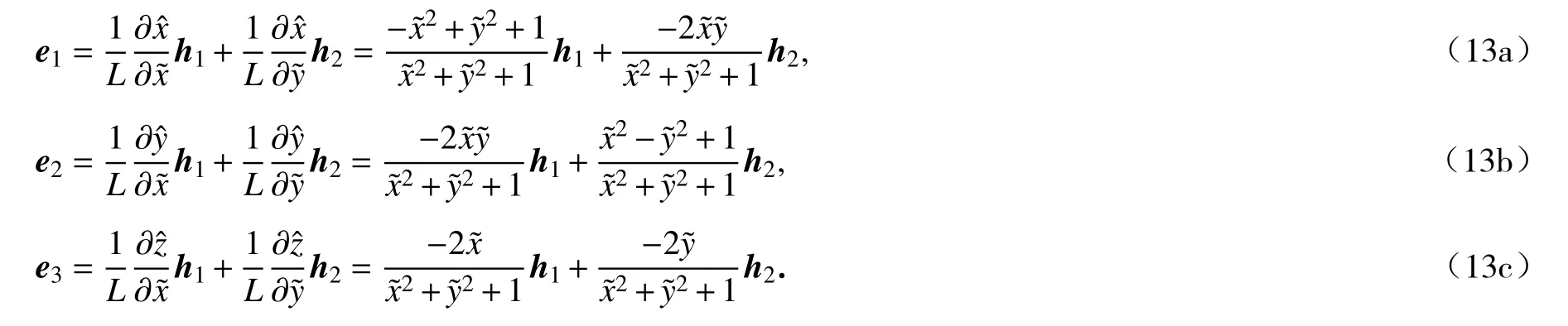
在计算空间内，基矢不再是常向量，而随着空间坐标变化而变化.通过基矢的变换（12）与逆变换（13）可以方便地求得在投影空间与物理空间的矢量之间的转换公式.例如，速度在投影空间与物理空间的分量具有以下关系：

使用基矢的逆变换（13）代入到速度定义（14）中，即可获得速度的逆变换公式：

在投影空间中求解控制方程(4)还需要计算矢量算符在投影空间中的形式.变换is的Jacobi 矩阵为

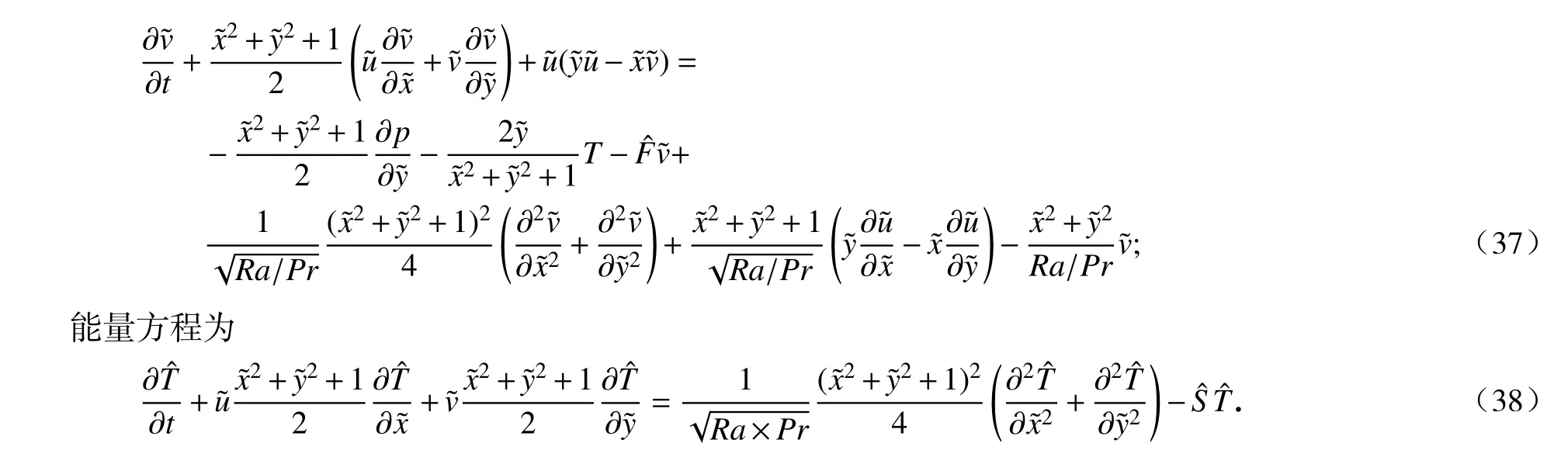
2 数值方法

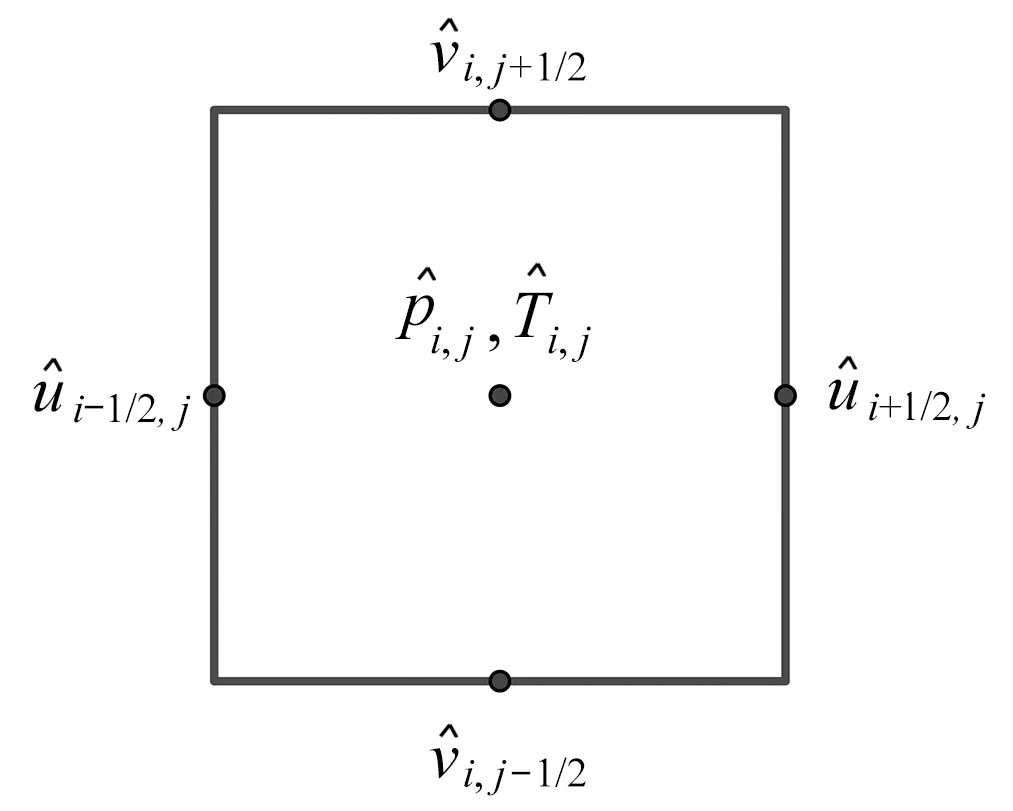
图2 交错网格示意图Fig.2 The scheme of the staggered mesh

图3 并行算法示意图Fig.3 The scheme of the parallel algorithm

3 结果讨论

3.1 算例信息与瞬时流场

本文一共设置了三个算例用以分析Rayleigh 数对流场的影响，三个算例的Ra分别为3×107，3×109和3×1011，详细信息见表 1.所有算例的Pr固定为7，因为肥皂水的物理性质与水近似.以往的研究表明Sˆ =Fˆ=0．06是一个合理的选择[19,21]，本文计算中也采用该值.为了消除网格分辨率对结果的影响，对每个算例都尝试了多个网格分辨率：256×256，512×512，1 024×1 024，1 536×1 536，2 048×2 048和2 560×2 560.图 4 显示了算例2 在不同网格分辨率下，系统总拟涡能随时间的变化曲线.从图中可以观察到，不同的网格分辨率下肥皂泡上的总拟涡能都在 50个无量纲时间单位内达到了统计稳态.在本文所有的数值模拟中，每个算例都保证足够的计算时长，使流场达到统计稳态，并对结果进行长时间的统计计算.随着网格分辨率的提升，总拟涡能的统计平均值在缓慢增加，但当网格分辨率超过2 048×2 048时，DNS 已可以获得网格独立结果.得益于并行计算效率的提升，本文首次使用2 048×2 048的网格分辨率开展了肥皂泡上热对流的DNS，同时也将DNS 的Rayleigh 数提升到Ra=3×1011.

图4 不同网格分辨率下，算例2 的总拟涡能随时间的变化曲线（左）和拟涡能总量的统计值随网格分辨率变化曲线（右）Fig.4 The temporal evolution of the total enstrophy on the bubble with different mesh resolutions(left)&the variation of the mean total enstropy with the mesh resolutions(right)

表1 算例参数信息Table 1 Information for the simulated cases

通过观察瞬态流场云图可以直观地分析肥皂泡上流场的宏观特点.图 5 展示了三个算例的瞬时温度场T，瞬时动能场u2/2和瞬时拟涡能场ω2/2.从图 5 中可以清晰地观察肥皂泡上非常卷曲的羽流以及尺度较大的岛涡.在经典的Rayleigh-Bénard 对流中，流场由冷热羽流所自组织的大尺度环流（large scale circulation）所主导.当对流槽具有特定的纵横比时，在合适的Rayleigh 数控制下，流场中还会出现角涡.肥皂泡没有冷边界，流场中不存在冷羽流；而肥皂泡同时也没有侧向边界及其形成的角涡，肥皂泡上的相干结构主要由热羽流及其演化形成.从温度云图上可以观察到，边界层上产生了大量的羽流，羽流在浮力的作用下向更高纬度运动.而同一时刻的拟涡能云图则显示羽流的形成与运动过程中产生了不同尺寸的涡，一些涡相互融合后形成了尺度较大的岛涡，岛涡主要居于较高纬度，与实验中观察到的情况相同[15,17].从动能云图中可以发现流场的动能集中在一些尺寸较大的岛涡中.

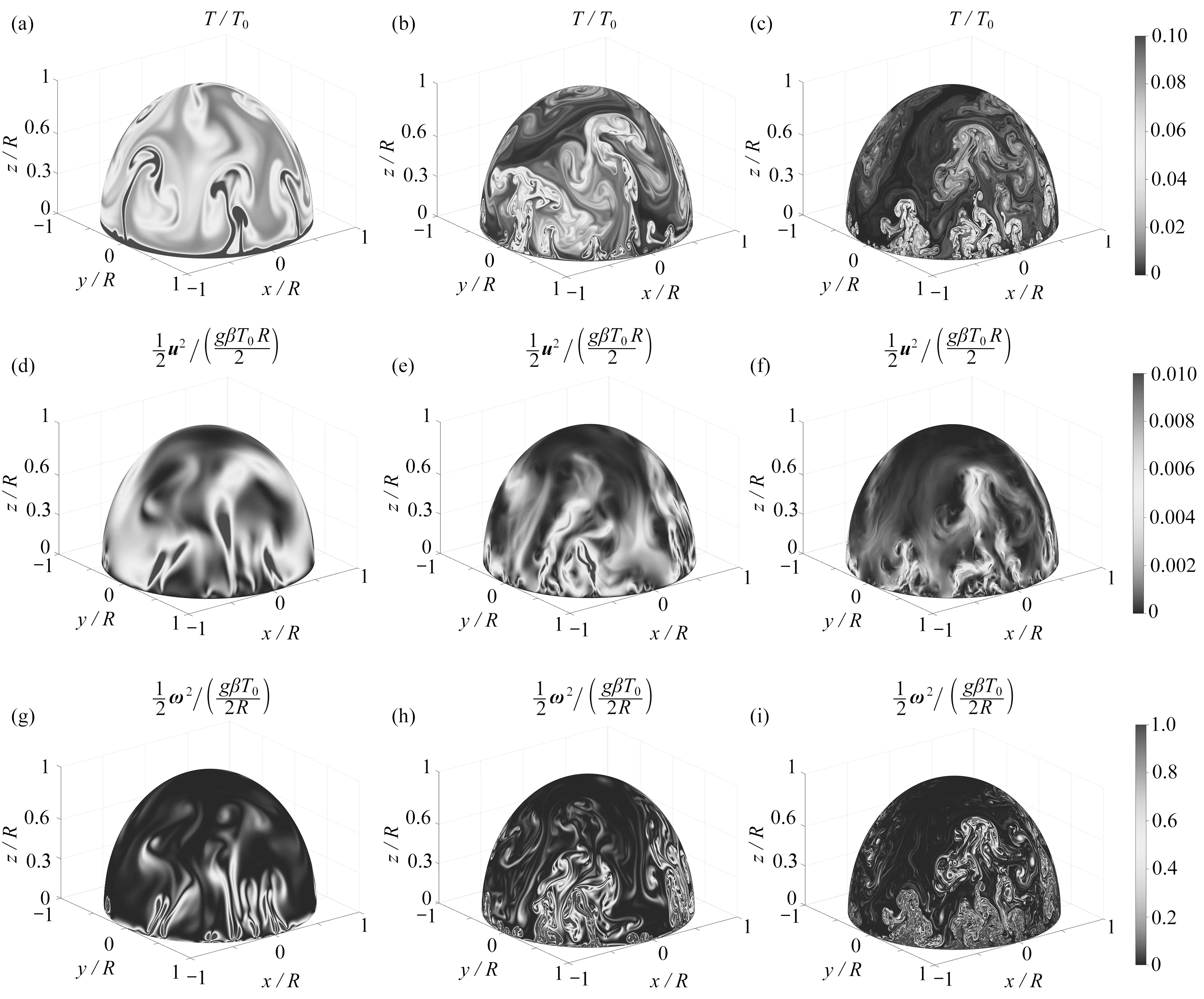
图5 瞬时流场图：（a）无量纲瞬时温度场，Ra=3×107；（b）无量纲瞬时温度场，Ra=3×109；（c）无量纲瞬时温度场，Ra=3×1011；（d）无量纲瞬时动能场，Ra=3×107；（e）无量纲瞬时动能场，Ra=3×109；（f）无量纲瞬时动能场，Ra=3×1011；（g）无量纲瞬时拟涡能场，Ra=3×107；（h）无量纲瞬时拟涡能场，Ra=3×109；（i）无量纲瞬时拟涡能场，Ra=3×1011Fig.5 The instantaneous flow field:(a)dimensionless instantaneous temperature field,Ra=3×107;(b)dimensionless instantaneous temperature field,Ra=3×109;(c)dimensionless instantaneous temperature field,Ra=3×1011;(d)dimensionless instantaneous kinetic energy field,Ra=3×107;(e)dimensionless instantaneous kinetic energy field,Ra=3×109;(f)dimensionless instantaneous kinetic energy field,Ra=3×1011;(g)dimensionless instantaneous enstrophy field,Ra=3×107;(h)dimensionless instantaneous enstrophy field,Ra=3×109;(i)dimensionless instantaneous enstrophy field,Ra=3×1011

而随着Ra的增加，瞬时流场出现了明显变化.当Ra=3×107时，羽流和涡的尺寸较大，动能分布在较大的流动结构中，而且可以从温度云图中清晰的观察到边界层.当Ra增加到3×109时，羽流更加细小与卷曲，而涡的尺寸也明显变小，同时羽流和涡的数量有明显增加，动能集中在更加细长的流动结构中.另外，温度边界层的厚度大幅减小，从温度云图中已经无法清晰观察到边界层.而当Ra=3×1011时，羽流和涡变得更加小，而其数量更进一步增加时，动能云图显示流动结构的尺寸将继续减小.

3.2 动能与拟热能的波数谱与通量

流场量的波数谱和通量表征了湍流场不同尺度的涡之间的相互作用，对于三维流场或二维平面流场，计算波数谱和通量需要进行空间Fourier 变换.肥皂泡上的流场具有曲面几何，需要专门的数学工具来计算波数谱和通量.任意球对称空间函数Ψ 均可以展开为球谐函数的级数：

在肥皂泡上寻找Bo59标度律需要考虑曲面几何带来的影响.由于肥皂泡上不同纬度上的重力投影随着纬度而变化，这是Bo59假设中所不包含的特点.这暗示只有在重力随纬度变化较小的区域内，有可能发现Bo59标度律.对于纬度为 θ*，重力加速度在球面切向的投影为gcosθ*，对之求 θ*的导数为gsinθ*，这说明越接近赤道重力投影随纬度的变化越小.然而，在导出Bo59标度律的理论中假定边界条件不产生影响，因而只有在足够远离赤道才能发现Bo59标度律.结合以上几点考虑，Bo59标度律只在一定纬度范围内有效.

本文三个算例的动能与拟热能的波数谱如图 6 所示，图中虚线为Bo59标度参考线.观察图 6 中的动能波数谱可以发现，在5≤kR≤100的范围内，Bo59标度律准确地描述了不同Ra下的动能谱随波数的标度规律.相反的是，图 6 中的拟热能的波数谱则表明，在本文所考虑的三个Ra条件下，肥皂泡的拟热能波数谱标度特征没有观察到Bo59标度律.在肥皂泡上流场中，边界层中流体的温度最高，而当流体随着羽流上升离开边界层后，温度快速下降.He 等[21]发现，边界层的平均温度与脉动温度均远大于肥皂泡其余部分，这暗示边界层对肥皂泡上温度场具有很强的影响.图 6 中的拟热能波数谱包含了整个肥皂泡上温度场的脉动信息，温度边界条件对波数谱的影响无法忽略，所以拟热能波数谱相比动能包含了更多边界的影响而没有Bo59标度律.随着Ra的增加，在小波数的范围内，动能谱和拟热能有较明显的减小，这与瞬时流场中羽流和涡的尺寸随着Ra增加而明显变小的规律相符合.对于图 6 中所有Ra的波数谱，随着波数k的增加，动能谱与拟热能谱逐渐减小.这表明肥皂泡上尺寸越大的流动结构具有更大的动能与拟热能，与从瞬时流场观察到的现象相同.

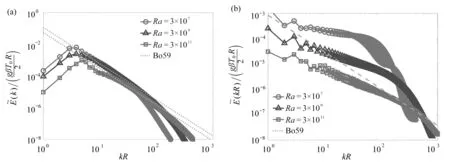
图6 动能与拟热能的波数谱：（a）动能；（b）拟热能Fig.6 The wave number spectra for the kinetic energy and entropy:(a)the kinetic energy;(b)the entropy

通量（flux）代表了湍流场中不同尺度的涡之间的物理量传递，大于0的通量表明物理量从大尺度的涡向小尺度的涡级串.反之当通量小于 0时，物理量从小尺度的涡向大尺度涡逆级串.Kraichnan[7]、Leith[8]和Batchelor[9]的二维湍流理论预言了双级串的现象：一个尺度范围中，动能能级逆级串而拟涡能保持正向级串.图 7 显示了整个肥皂泡上动能、拟涡能、拟热能和浮力项的通量，图中包含全部三个算例的结果.在三个不同的Ra条件下，图 7 中的 ΠE曲线都具有相同的规律，在较小波数的区间ΠE＞0，随着波数的增加，ΠE快速减小到负值.在 ΠE达到最小值之后，ΠE随着波数的增加逐渐增加，重新达到ΠE＞0，此时 ΠE随波数的变化较小.三个算例中的流场均出现了动能能级逆级串的现象，随着Ra的增加，能级拟级串的尺度区间逐渐变大.

通过观察图 7 中的拟涡能通量曲线可以发现，三个算例的 ΠW始终大于0，肥皂泡上拟涡能始终保持从大涡向小涡的传递方向.在不同的Ra下，ΠW在较小波数的范围内保持稳定，但随着波数的增加，ΠW先快速增加，达到最大值之后又快速减少.三个算例的拟热能的通量同样始终大于0，这说明温度也始终是由较大的涡传递给较小的涡.从瞬时温度场可以观察到，羽流和涡在赤道处产生时尺寸较大，在向高纬度运动的过程中破碎消散，这一过程符合拟热能通量所描述的逆热能传递特征.当Ra=3×1011与Ra=3×109时，ΠT随着波数的增加单调缓慢减小.而在Ra=3×107的条件下，拟涡能通量曲线随着波数的增加先增加后减小，出现一个极大值.

浮力通量是对整个肥皂泡上的浮力场Teθ*进行球谐分解后计算获得，计算方法与动能的通量计算方法相同.由于肥皂泡上的流体运动是由浮力所驱动，浮力通量具有特别的重要性.图 7 中的浮力通量曲线显示三个算例的ΠBuoy始终大于0.不同Ra下的浮力通量曲线具有相同的变化规律.在区间kR≤5中，ΠBuoy随着波数增加保持稳定.在kR≥10的条件下，浮力通量随着波数的增加而增加，达到最大值之后又快速减小.ΠBuoy的上升暗示一个在较小尺度上存在局部的湍流动能注入，而这个湍流动能注入来源是动能能量逆级串：小尺度涡向大尺度涡注入了湍流动能.随着Ra的增加，ΠBuoy显著减小.由于Ra的增加会使得羽流的尺寸快速减小，而且小尺寸的热羽流受到的浮力更小，于是浮力通量在整个波数范围上都减小了.

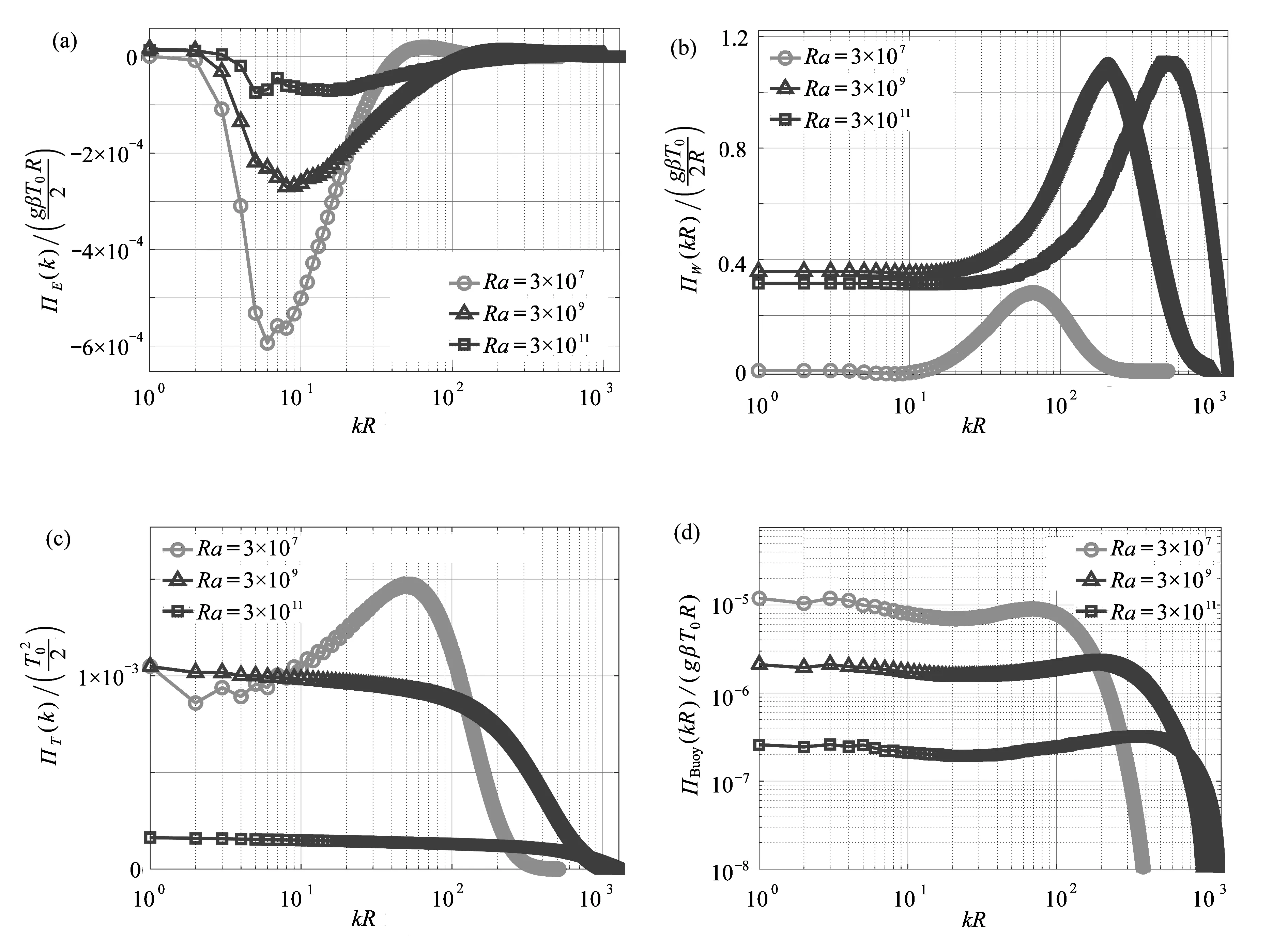
图7 肥皂泡上的动能通量、拟涡能通量、拟热能通量和浮力的通量：（a）动能；（b）拟涡能；（c）拟热能；（d）浮力Fig.7 The fluxes of kinetic energy,enstrophy,entropy and buoyancy on the soap bubble:(a)the kinetic energy;(b)the enstrophy;(c)the entropy;(d)the buoyancy

3.3 结构函数

Kolmogrov 在1941 年提出各向同性均匀湍流假设，并使用结构函数来描述不同尺度涡之间的能量交换.结构函数被定义在物理空间中，更加直观地揭示出流场脉动的特点，并且能够给出更高阶的流场信息.n阶速度结构函数的定义如下：

x是空间中一点的位置矢量，而d为距离矢量，d=|d|，n为正整数，〈·〉算符代表系综平均.按照同样的方法，可以定义n阶温度结构函数：

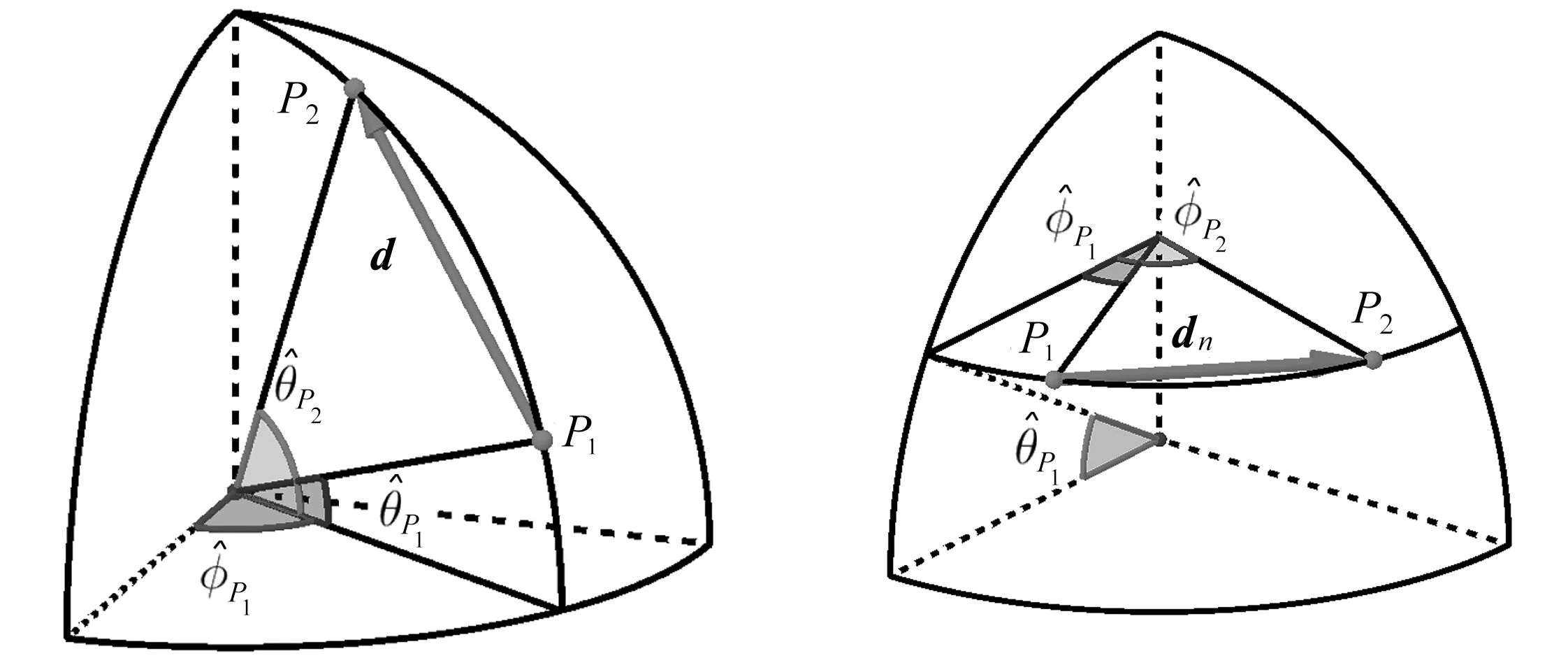
图8 结构函数计算方法Fig.8 The scheme of the distance for calculating the structure function

由于温度场与速度场的具有连续性，当d足够小时，温度与速度结构函数的标度系数退化为n以满足Taylor 展开特性.在计算结构函数时，需要对物理量的差值进行时间，经度和纬度上的平均.所有达到统计平衡态之后的时间步都在时间平均的范围内，而经度平均的范围在0◦≤ϕ*≤360◦.为了能在消除边界层的影响同时保证计算的准确性，纬度平均的范围被限制在10◦≤θ*≤90◦.图 9 显示了纬度与经度方向上的从2 到9 阶结构函数，其中纬度方向上的结构函数在左边，经度方向上的结构函数在右边.将纬度方向上的温度或速度结构函数与经度方向上的结构函数相对比，可以发现两者的标度规律非常接近，但是数值有一些微小的差别.这与Bo59标度律成立的前提条件相符合：速度或温度的差值仅与两点之间的距离相关，与方向无关.

图9 纬度与经度方向上2 到9 阶的温度和速度结构函数：（a）纬度方向的温度结构函数；（b）纬度方向的速度结构函数；（c）经度方向的温度结构函数；（d）经度方向的速度结构函数Fig.9 The temperature and velocity structure functions in the latitude and longitude directions,n=2～9:(a)the temperature structure functions in the latitude direction;(b)the velocity structure functions in the latitude direction;(c)the temperature structure functions in the longitude direction;(d)the velocity structure functions in the longitude direction

从图 9 可以观察到，速度结构函数在d/R≤O(0．01)的范围内，标度系数为n.而在0．01≤d/R≤0．1的区间中，Bo59标度律较好地描述了速度结构函数的标度特征.在阶数n逐渐增加的情况下，速度结构函数始终能在同一区间内较好地满足Bo59标度律，但受到湍流间歇的影响，其指数在高阶时并非线性增加.

另一方面，观察温度结构函数曲线上可以发现，温度结构函数在d/R≤O(0．01)的区间内满足而在 0．01≤d/R≤0．1的区间内较好地符合Bo59标度律.由于排除了边界层的影响，结构函数得到的结果与波数谱不同.

4 结论与展望

本文介绍了底部加热的半个肥皂泡这一新的准二维湍流，同时详细介绍了其DNS 方法.计算中针对肥皂泡二维球面的曲面几何特点，借助球极投影，将物理空间的控制方程转换到投影坐标系中，降低了离散化控制方程的难度.此后还介绍了球面上利用球谐分解计算波数谱与通量，以及计算结构函数的分析方法.最后，针对Ra=3×107，Ra=3×109，Ra=3×1011三个算例，本文计算了动能和拟热能的波数谱，以及动能、拟热能、拟涡能和浮力的通量.另外也计算了Ra=3×1011算例的温度与速度结构函数.不同Ra的结果都表明了肥皂泡上存在二维湍流中双级串的现象.湍流动能波数谱较好地满足了Bo59标度律的理论预示，但拟热能由于主要受边界的影响较大，其波数谱中没有观察到足Bo59标度律.但通过湍流结构函数，在去除了赤道边界的高温边界层影响后，无论速度还是温度结构函数，都在一定范围较好地符合Bo59的理论预示.未来可进一步通过增加Rayleigh 数范围，研究Rayleigh 数与能量注入尺度以及不同维度上浮力作用间的联系.