一类带有变指数非局部项的反应扩散方程解的爆 破 行 为*

田 娅，秦 瑶，向 晶

（重庆邮电大学 理学院，重庆 400065）

引言

反应扩散方程是一类非常重要的偏微分方程，通常用来解释和预测自然界中广泛存在的扩散现象.本文将考虑如下带有变指数非局部项的扩散方程：

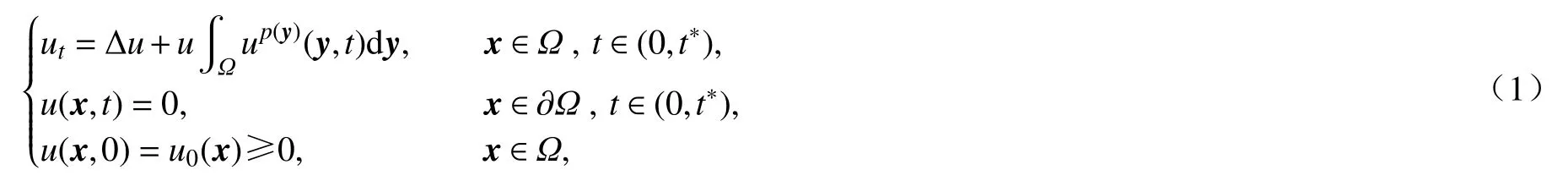
其中m≥2，p(x)＞1.利用能量方法，他们得到了类似文献[12]的结果.即初始能量足够大时，解在有限时刻爆破.进一步地，Baghaei 等在文献[15] 中给出了问题(4)解的爆破时间下界估计.在爆破问题的研究中，通常使用的研究方法(上下解方法、能量方法等)一般可以直接导出爆破时间的上界.然而，在实际问题中，对爆破时间下界的估计往往具有更重要的应用参考价值.

据笔者所知，对于问题(1)解的有限时间爆破行为，目前尚无学者进行研究.因此，受上述文献的启发，本文将讨论问题(1)的解的爆破问题，给出爆破发生的条件，并对爆破时间的上、下界进行估计.全文结构如下：首先，由不动点定理，证明问题(1)解的局部存在性和唯一性；其次，利用上下解方法，给出问题(1)的解在有限时刻爆破的充分条件；接下来，利用能量估计方法，借助辅助函数以及一些不等式给出爆破时间的下界估计；最后，通过举例验证了本文结论的可行性.

1 解的局部存在性

2 解在有限时刻爆破

3 爆破时间下界估计

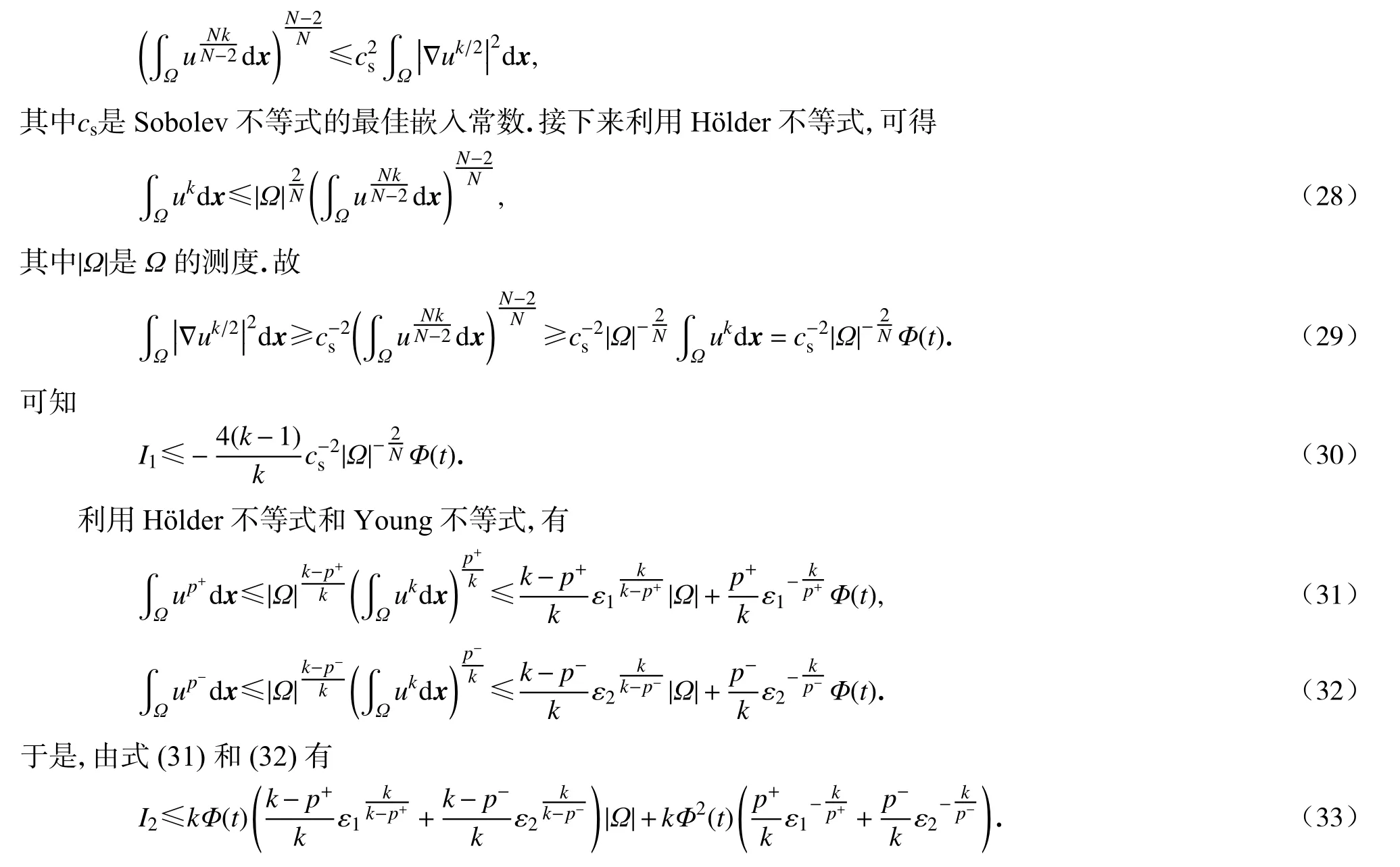
4 应用举例

5 结论

本文研究了一类具有变指数项的反应扩散方程的爆破问题.通过上下解方法、能量估计及各种不等式技巧给出了问题解在有限时间发生爆破的充分条件，并得到了爆破时间的上下界估计.最后通过实例对结论进行验证.从实例中可以看出，爆破时间的上、下界估计比较接近，说明定理中给出的时间界限估计较为准确，具有一定的参考价值.

由于反应项中存在变指数，给爆破发生的临界指数的确定带来了很大的困难，因此本文只给出了爆破发生的充分条件.对于必要条件还须寻求新技术作进一步探讨.