时间周期的离散SIS 模型的传播动力学*

陈 妍

（西安电子科技大学 数学与统计学院，西安 710071）

引言

为有效预防和控制疾病的流行，大量的数学模型被用于研究传染病的动力学行为[1-9].针对确定性传染病在多种群中的空间传播问题，Rass 与Radcliffe[4]提出了以下多种群SIS 传染病模型：

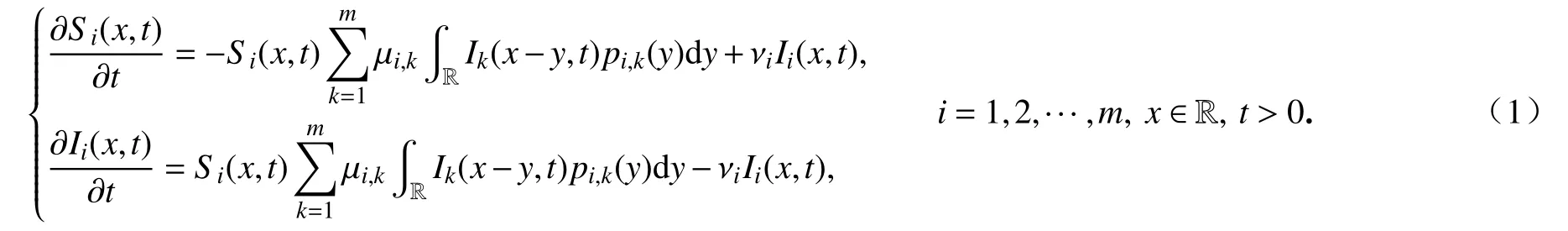
该模型描述了一个没有出生、死亡、迁入、迁出的封闭系统，或者一个出生率和迁入率由死亡率和迁出率平衡的开放系统.其中Si(x,t)和Ii(x,t)分别表示第i个种群中位于x处、t时刻感染个体和易感个体的数量，µi,k表示第i个种群中的易感者与第k个种群中的感染者之间的感染率，pi,k(·)是相应的接触分布.νi≥0表示第i个种群中感染者的移出率，包含感染个体的死亡率、迁出率和恢复率.假设第i个种群的个体总量为 σi，则σi=Si(x,t)+Ii(x,t)，进而系统(1)可写为

1 准备知识

2 渐近传播速度与周期行波解

3 结论

本文研究了一类具有时间周期的空间离散多种群SIS 模型的传播动力学.首先，借助周期单调半流的传播速度与行波理论，证明了渐近传播速度c*的存在性.其次，利用比较原理，证得了渐近传播速度即为单调周期行波解的最小波速.这些结论能够更好地揭示该疾病的流行规律，从而起到很好的防护作用，因此对该传染病传播动力学的研究具有一定的理论价值和实际意义.而对于周期行波解的稳定性，这将是笔者下一步需要解决的问题.