一类分数阶修正的不稳定Schrödinger方程的新精确解*
2022-11-09刘静静孙峪怀
刘静静,孙峪怀
(四川师范大学 数学科学学院,成都 610066)
引言

1 解的构建






③当Δ=0时,方程(1)有如下的有理函数形式解:

图1 λ=3,µ=2,K=1,v=1,β=-1,c=1,s=-15,α=1/2时,q2.1.1的图像Fig.1 The graphic corresponding to q2.1.1(λ=3,µ=2,K=1,v=1,β=-1,c=1,s=-15,α=1/2)
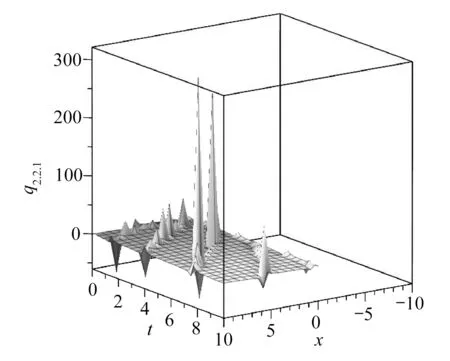
图2 λ=2,µ=2,K=1,v=1,β=-1,c=1,s=-5,α=1/2时,q2.2.1的图像Fig.2 The graphic corresponding to q2.2.1(λ=2,µ=2,K=1,v=1,β=-1,c=1,s=-5,α=1/2)
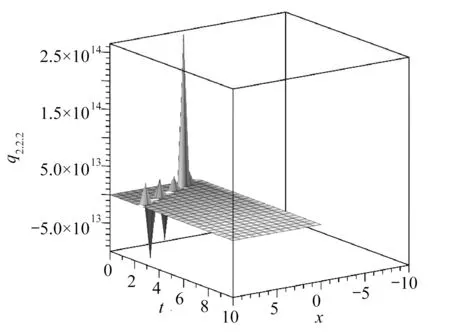
图3 λ=2,µ=2,K=1,v=1,β=-1,c=1,s=-5,α=1/2时,q2.2.2的图像Fig.3 The graphic corresponding to q2.2.2(λ=2,µ=2,K=1,v=1,β=-1,c=1,s=-5,α=1/2)

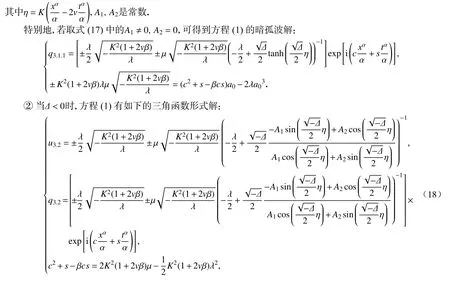




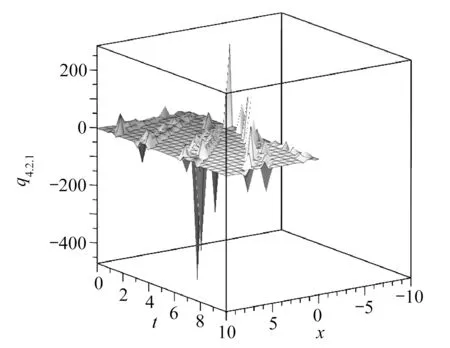
图4 λ=2,µ=2,K=1,v=1,β=-1,c=1,α=1/2时,q4.2.1的图像Fig.4 The graphic corresponding to q4.2.1(λ=2,µ=2,K=1,v=1,β=-1,c=1,α=1/2)

2 结论
本文研究了FMUSE,先对方程进行分数阶复变换转化为常微分方程,再分离实部和虚部并分别令其为零,得到了色散关系.对Riccati 方程,利用修改的(G′/G)-展开法,构建了一系列带参数的精确行波通解,其中包括有理函数解、三角函数解和双曲函数解.将所得结果与文献[1]中的解进行比较,q2.2,q2.2.1,q2.2.2,q3.2,q3.2.1,q3.2.2,q4.2,q4.2.1,q4.2.2是本文求得的新解.通过绘图软件,给出典型参数下代表性孤波解图像,这有助于直观了解孤波传输图案和应用上用不同参数作物理控制.
